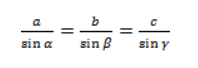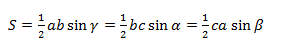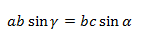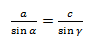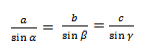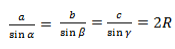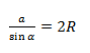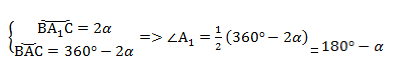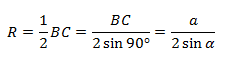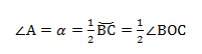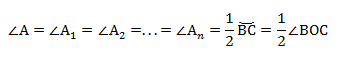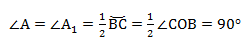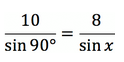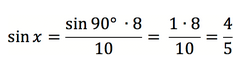Как найти синус в четырехугольнике (4 видео)

Теорема синусов

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Содержание

Доказательство теоремы синусов
Доказательство следствия из теоремы синусов
Теорема о вписанном в окружность угле
Примеры решения задач
Запоминаем
Теорема синусов. Доказательство
Примеры и решения
Четырехугольники. Основные теоремы, формулы и свойства. Виртуальный справочник репетитра по математике
🔥 Видео

Видео:Геометрия 8. Урок 12 - Площадь четырехугольников. Формулы.Скачать

Доказательство теоремы синусов

Теорема синусов звучит так: стороны треугольника пропорциональны синусам противолежащих углов.

Нарисуем стандартный треугольник и запишем теорему формулой:

Формула теоремы синусов:

Докажем теорему с помощью формулы площади треугольника через синус его угла.

Из этой формулы мы получаем два соотношения:

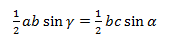
На b сокращаем, синусы переносим в знаменатели:

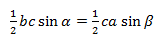
bc sinα = ca sinβ

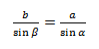
Из этих двух соотношений получаем:

Теорема синусов для треугольника доказана.

Эта теорема пригодится, чтобы найти:

Стороны треугольника, если даны два угла и одна сторона.
Углы треугольника, если даны две стороны и один прилежащий угол.

Видео:Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать

Доказательство следствия из теоремы синусов

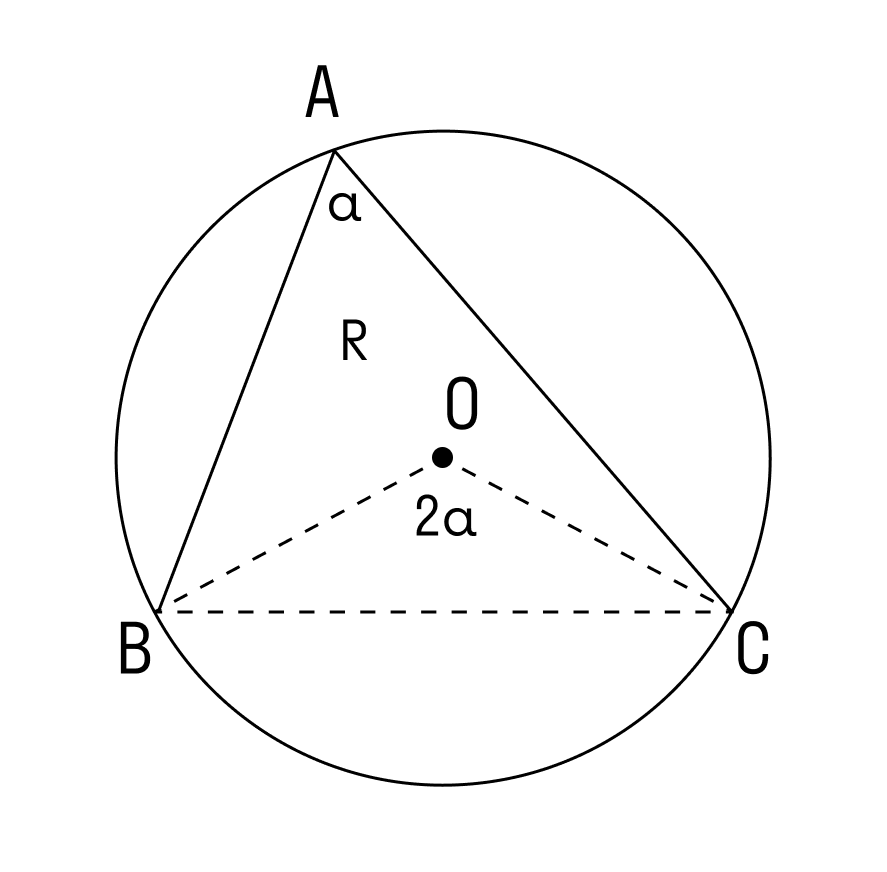
У теоремы синусов есть важное следствие. Нарисуем треугольник, опишем вокруг него окружность и рассмотрим следствие через радиус.

где R — радиус описанной около треугольника окружности.

Так образовались три формулы радиуса описанной окружности:

Основной смысл следствия из теоремы синусов заключен в этой формуле:

Радиус описанной окружности не зависит от углов α, β, γ. Удвоенный радиус описанной окружности равен отношению стороны треугольника к синусу противолежащего угла.

Для доказательства следствия теоремы синусов рассмотрим три случая.

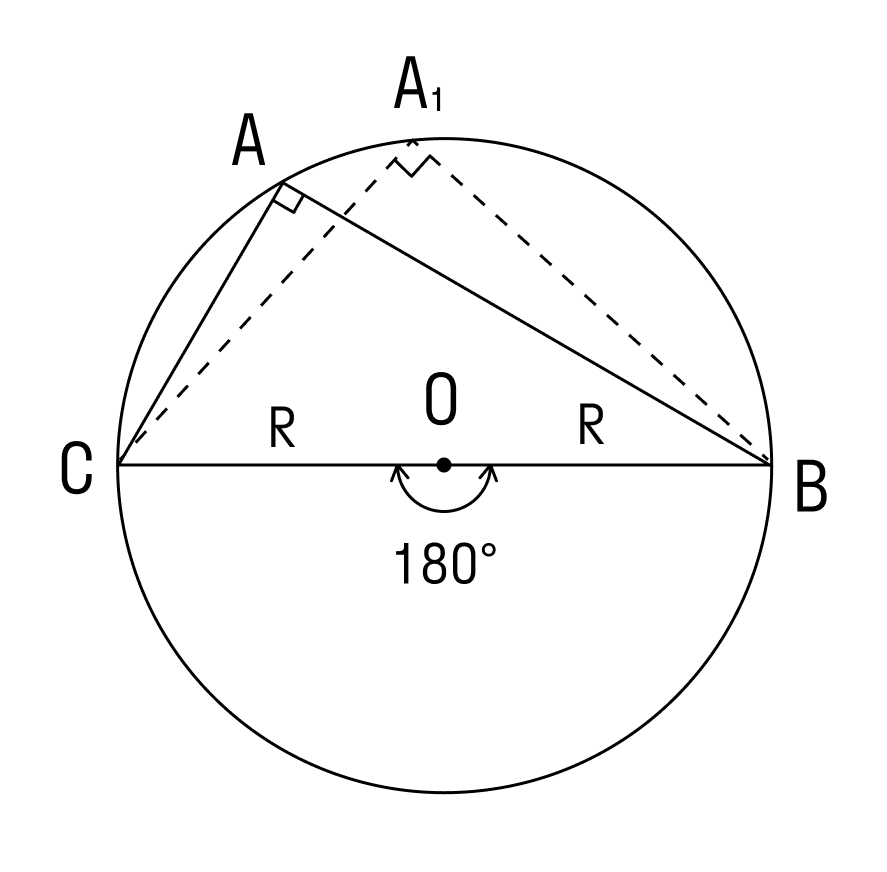
1. Угол ∠А = α — острый в треугольнике АВС.

Проведем диаметр BA1. В этом случае точка А и точка А1 лежат в одной полуплоскости от прямой ВС.

Используем теорему о вписанном угле и видим, что ∠А = ∠А1 = α. Треугольник BA1C — прямоугольный, в нём ∠ BCA1 = 90°, так как он опирается на диаметр BA1.

Чтобы найти катет a в треугольнике BA1C, нужно умножить гипотенузу BA1 на синус противолежащего угла.

BA1 = 2R, где R — радиус окружности

Следовательно: R = α/2 sinα

Для острого треугольника с описанной окружностью теорема доказана.

2. Угол ∠А = α — тупой в треугольнике АВС.

Проведем диаметр окружности BA1. Точки А и A1 по разные стороны от прямой ВС. Четырёхугольник ACA1B вписан в окружность, и его основное свойство в том, что сумма противолежащих углов равна 180°.

Следовательно, ∠А1 = 180° — α.

Вспомним свойство вписанного в окружность четырёхугольника:

Также известно, что sin(180° — α) = sinα.

В треугольнике BCA1 угол при вершине С равен 90°, потому что он опирается на диаметр. Следовательно, катет а мы находим таким образом:

α = 2R sin (180° — α) = 2R sinα

Следовательно: R = α/2 sinα

Для тупого треугольника с описанной окружностью теорема доказана.

Часто используемые тупые углы:

sin120° = sin(180° — 60°) = sin60° = 3/√2;
sin150° = sin(180° — 30°) = sin30° = 1/2;
sin135° = sin(180° — 45°) = sin45° = 2/√2.

3. Угол ∠А = 90°.

В прямоугольнике АВС угол А прямой, а противоположная сторона BC = α = 2R, где R — это радиус описанной окружности.

Для прямоугольного треугольника с описанной окружностью теорема доказана.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.

Видео:ОГЭ как найти тангенс угла, если нет треугольника #математика #огэ #огэматематика #геометрияСкачать

Теорема о вписанном в окружность угле

Из теоремы синусов и ее следствия можно сделать любопытный вывод: если известна одна сторона треугольника и синус противолежащего угла — можно найти и радиус описанной окружности. Но треугольник не задаётся только этими величинами. Это значит, что если треугольник еще не задан, найти радиус описанной окружности возможно.

Раскроем эту тему на примере теоремы о вписанном в окружность угле и следствиях из нее.

Теорема о вписанном угле: вписанный в окружность угол измеряется половиной дуги, на которую он опирается.

∠А = α опирается на дугу ВС. Дуга ВС содержит столько же градусов, сколько ее центральный угол ∠BOC.

Формула теоремы о вписанном угле:

Следствие 1 из теоремы о вписанном в окружность угле

Вписанные углы, опирающиеся на одну дугу, равны.

∠А = ∠BAC опирается на дугу ВС. Поэтому ∠A = 1/2(∠COB).

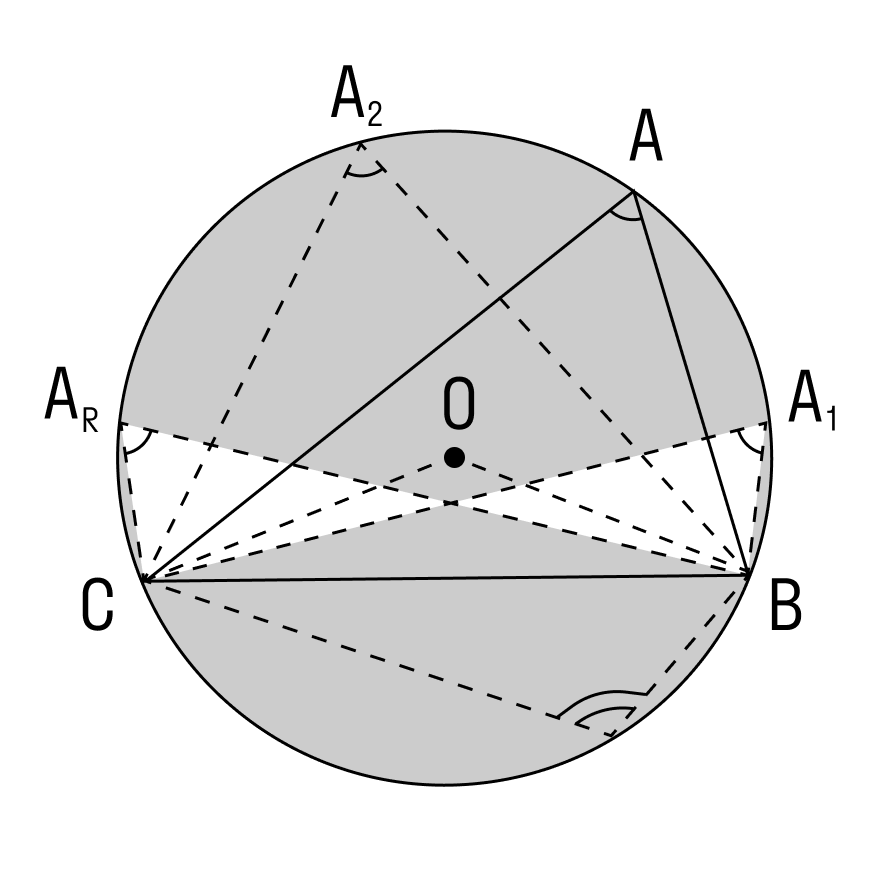
Если мы возьмём точки A1, А2. Аn и проведём от них лучи, которые опираются на одну и ту же дугу, то получим:

На рисунке изображено множество треугольников, у которых есть общая сторона СВ и одинаковый противолежащий угол. Треугольники являются подобными, и их объединяет одинаковый радиус описанной окружности.

Следствие 2 из теоремы о вписанном в окружность угле

Вписанные углы, которые опираются на диаметр, равны 90°, то есть прямые.

ВС — диаметр описанной окружности, следовательно ∠COB = 180°.

Следствие 3 из теоремы о вписанном в окружность угле

Сумма противоположных углов вписанного в окружность четырёхугольника равна 180°. Это значит, что:

Угол ∠А = α опирается на дугу DCB. Поэтому DCB = 2α по теореме о вписанном угле.

Угол ∠С = γ опирается на дугу DAB. Поэтому DAB = 2γ.

Но так как 2α и 2γ — это вся окружность, то 2α + 2γ = 360°.

Следовательно: α + γ = 180°.

Поэтому: ∠A + ∠C = 180°.

Следствие 4 из теоремы о вписанном в окружность угле

Синусы противоположных углов вписанного четырехугольника равны. То есть:

sinγ = sin(180° — α)

Так как sin(180° — α) = sinα, то sinγ = sin(180° — α) = sinα

Видео:Спидран: Как запомнить таблицу синусов и косинусов за 1 минуту? Евгений ДолжкевичСкачать

Примеры решения задач

Теорема синусов и следствия из неё активно используются при решении задач. Рассмотрим несколько примеров, чтобы закрепить материал.

Пример 1. В треугольнике ABC ∠A = 45°,∠C = 15°, BC = 4√6. Найти AC.

∠B = 180° — 45° — 15° = 120°

Сторону AC найдем по теореме синусов:

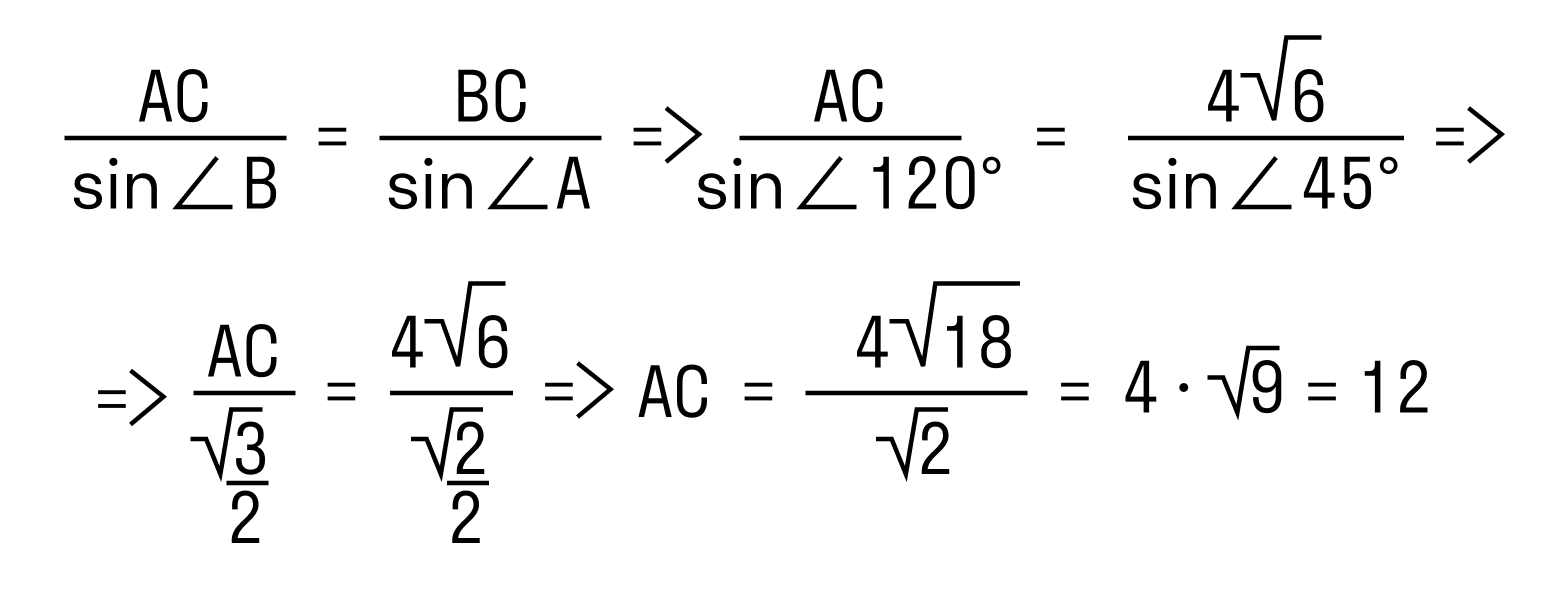
Пример 2. Гипотенуза и один из катетов прямоугольного треугольника равны 10 и 8 см. Найти угол, который расположен напротив данного катета.

В этой статье мы узнали, что в прямоугольном треугольнике напротив гипотенузы располагается угол, равный 90°. Примем неизвестный угол за x. Тогда соотношение сторон выглядит так:

Значит x = sin (4/5) ≈ 53,1°.

Ответ: угол составляет примерно 53,1°.

Видео:Как просто запомнить, что такое sin, cos, tg?! #косинус #синус #тангенс #математика #огэ #егэСкачать

Запоминаем

Обычная теорема: стороны треугольника пропорциональны синусам противолежащих углов.

Расширенная теорема: в произвольном треугольнике справедливо следующее соотношение:

Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Теорема синусов. Доказательство

Теорема 1 (теорема синусов). Стороны треугольника пропорциональны синусам противолежащих углов:

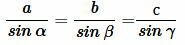(a)

Доказательство. Пусть задан треугольник ABC. Проведем высоту h_b из вершины B на сторону b (Рис.1).

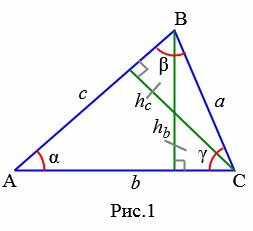Из определения синуса (см. страницу Синус и косинус. Онлайн калькулятор) следует, что синус угла α равен h_b если предполагать, что c=1. Но поскольку c может иметь любое значение, то имеем

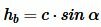Аналогично можем записать:

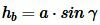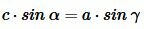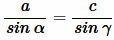(1)

Далее, для высоты h_c, опущенной из вершины C на сторону c, имеем:

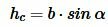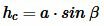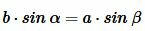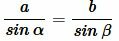(2)

Из (1) и (2) получим:

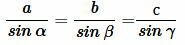Теорема 2 (расширенная теорема синусов). Для произвольного треугольника справедливо следующее равенство:

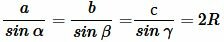(b)

где a, b, c стороны треугольника, а α, β, γ противолежащие им углы, соответственно, R− радиус описанной около треугольника окружности.

Доказательство. Пусть задан треугольник ABC и описанная окружность с радиусом R, проходящей через вершины треугольника.

В теореме 1 мы доказали справедливость равенства (a). Для доказательства (b) достаточно показать, что

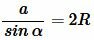(3)

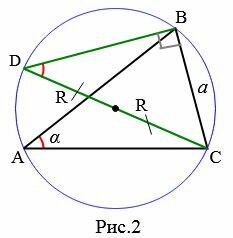
Проведем через вершину C диаметр CD описанной окружности и соединим точки D и B.

1. Пусть точки D и A лежат по одну сторону от BC (Рис.2). Полученный треугольник BCD являестся прямоугольным треугольником с прямым углом B, поскольку его одна сторона совпадает с диаметром окружности. А для этого прямоугольного треугольника справедливо равенство:

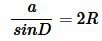Но 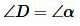поскольку обе эти углы опираются на дугу BC. Отсюда следует справедливость равенства (3).

2. Пусть точки D и A лежат в разные стороны от BC (Рис.3).

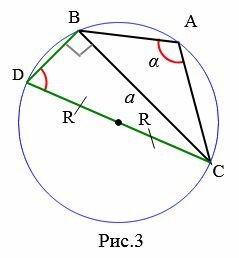Поскольку BCD прямоугольный треугольник, то справедливо следующее равенство:

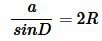(4)

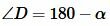
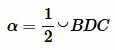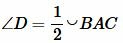Покажем, что . Действительно. Так как вписанный угол измеряется половиной дуги, на которой он упирается, то имеем:

(5)

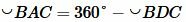(6)

Тогда из (5) и (6) получим:

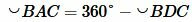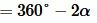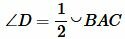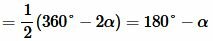(7)

Учитывая (7), уравнение (4) можно записать так:

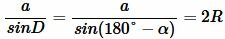(8)

Но 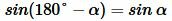. Тогда из (8) получим равенство (3).

Видео:ТРИГОНОМЕТРИЯ | Синус, Косинус, Тангенс, КотангенсСкачать

Примеры и решения

Задание 1. В треугольнике ABC a=8, c=10, угол α=30°. Найти сторону b (Рис.4).

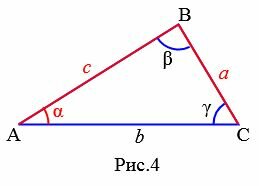Решение. Из теоремы синусов, имеем:

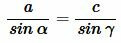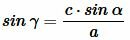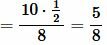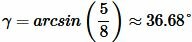Поскольку сумма всех углов треугольника равна 180°, то β=180°−30°−36.68°=113.32°.

Далее, из теоремы синусов:

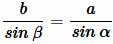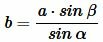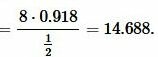Задание 2. В треугольнике ABC c=16, α=30°, β=45°. Найти стороны a, b (Рис.5).

Видео:#58. Олимпиадная задача о четырехугольникеСкачать

Четырехугольники. Основные теоремы, формулы и свойства. Виртуальный справочник репетитра по математике

З десь ученики и репетиторы по математике и могут найти основные свойства и формулы площадей четырехугольников, изучаемых в школе по основной программе. Регулярно пользуюсь этими теоретическими сведениями на тематических и обзорных занятиях по геометрии (планиметрии), а также при подготовке к ЕГЭ по математкие. Все математические понятия и факты иллюстрированы с цветовыми выделениями главных особенностей изучаемого.

1) Площади четырехугольников

Площадь параллелограмма

произведение основания на высоту

пороизведение сторон на синус угла между ними

полупроизведение диагоналей на синус угла между ними

Площадь трапеции

произведение полусуммы оснований на высоту

произведение средней линии на высоту

полупроизведение диагоналей на синус угла между ними

Площадь произвольного четырехугольника

Площадь произвольного четырехугольника равна полупроизведению его диагоналей на синус угла между ними

2) Свойства параллелограмма

В параллелограмме:
противолежащие стороны и углы равны

диагонали пересекаются и в точке пересечения делятся пополам

3) сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон, то есть

3) Cредняя линия в трапеции

Теорема о средней линии: Средняя линия трапеции параллельна основаниям и равна их полусумме.
То есть и

4) Средняя линия в равнобедренной трапеции

Средняя линия в равнобедренной трапеции равна отрезку нижнего основания, соединяющему вершину основания с снованием проведенной к ней высоты.

То есть

5) Теорема с сдвиге диагонали в трапеции

Теорема: Если в трапеции через вершину В, как показано на рисунке слева , провести отрезок параллельный одной из диагоналей, то окажутся верными следующие факты:

трапеция — равнобедренная равнобедренный

6) Четыре замечательные точки в трапеции

Теорема: В любой трапеции точка пересечения диагоналей, точка пеерсечения продолжений боковых сторон и середины оснований лежат на одной прямой.

То есть точки M, N, K и P лежат на одной прямой

Комментарий репетитора по математкие: Знаний этих свойств по четырехугольникам вполне достаточно для решения задачи С4 на ЕГЭ, то есть ничего сверх этих фактов по четырехугольникам абитуриент знать не обязан. Однако сильным ученикам для решения сложных задач части С или олимпиадных геометрических задач, а также для качественной подготовки к экзамену по математике в МГУ необходимо расширить список. Я бы не советовал репетиторам ограничиваться только задачами на применение этих свойств, так как составителями ЕГЭ по математике закладывается проверка сразу нескольких навыков работы с теорией. В течении всего времени подготовки к ЕГЭ репетитору по математкие необходимо отбирать тренировочные задачи на одновременное использование этих свойств с другими планиметрическими фактами внутри одной задачи, ибо на экзамене может встретиться многоходовая комбинация.

Колпаков Александр Николаевич. Репетитор по математике.

Александр, конечно, есть множество карманных справочников, НО! Было бы здорово сделать для репетиторов по математике скачиваемые материалы в каком-нибудь удобном формате, а также для проработки отдельно задачи к таким шпаргалкам опять же от простого к сложному.

Я выкладывал на каких-то страницах с карточками-памятками готовые теоретические материалы — файлы в формате word, по крайней мере для планиметрии точно. Просмотрите соответствующие разделы сайта. На них ведут ссылки с главной страницы. Задумываю выделить репетиторам по математике для скачивания материалов отдельный раздел сайта. Все упирается в мою занятость реальными учениками. Иначе бы уже давно реализовал все замыслы.

В этой хорошей подборке, на мой взгляд, не достает сведений по углам, например, два внутренних угла параллелограмма, связанных одной стороной в сумме дают 180 градусов.

Принципиально ли в формуле площади через диагонали брать именно меньший угол между ними? Или можно любой?

Александр, если не затруднит, очень хотелось бы получить файлик world на почту или тыкнуть ссылкой на нее. За ранее очень благодарен за титанический труд.