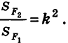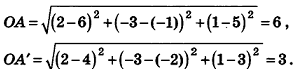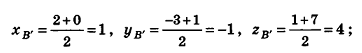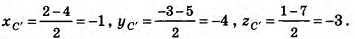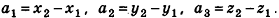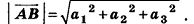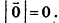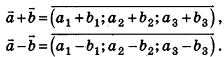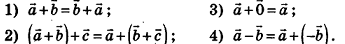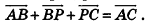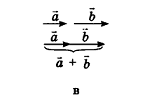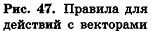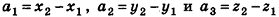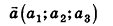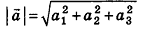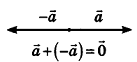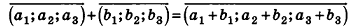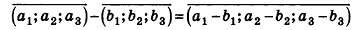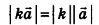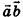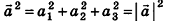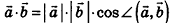Содержание:
Как известно, расположение точки на координатной прямой однозначно описывается одной координатой. Из курса планиметрии вы знакомы с прямоугольной декартовой системой координат на плоскости. Напомним, что для ее введения через произвольную точку плоскости О проводят две взаимно перпендикулярные координатные оси Ох и Оу (рис. 1). При таких условиях каждой точке плоскости А ставится в соответствие упорядоченная пара чисел (х;у) — координаты оснований перпендикуляров
Вполне естественно, что для описания расположения точки в пространстве необходимо иметь три координаты — ведь, например, бабочка перемещается в воздухе не только вперед-назад и вправо-влево, но и вверх-вниз.
Итак, рассмотрим три взаимно перпендикулярные координатные оси 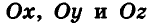
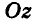
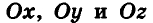
Для определения координат произвольной точки пространства А проведем из данной точки перпендикуляры 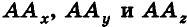
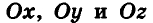
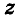
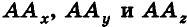
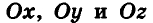
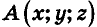
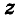
Координаты точки А можно определить и по-иному. Например, для получения координаты Ах проведем перпендикуляр АА0 к плоскости Оху, а потом из точки А0 проведем перпендикуляр 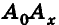
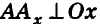
Значения координат точки А можно также получить, если провести через эту точку три плоскости, параллельные координатным плоскостям 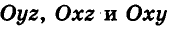
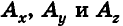
Итак, в прямоугольной декартовой системе координат каждой точке пространства ставится в соответствие единственная упорядоченная тройка чисел (x;y;z), и наоборот: каждой тройке чисел (x;y;z) соответствует единственная точка пространства.
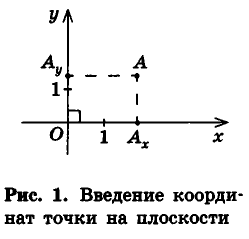
Очевидно, что если точка принадлежит одной из координатных плоскостей, то некоторая ее координата равна нулю. Так, на рисунке 4 точка М принадлежит плоскости Оху и имеет координаты (2;-1;0), а точка N плоскости Оуг — координаты (0; 2; — 3). Соответственно точки, принадлежащие координатным осям, имеют две нулевые координаты: например, координаты точки К оси Ог равны (0; 0; 2). Очевидно также, что все три координаты начала координат нулевые: 0(0;0;0). Условия, при которых та или иная координата точки равна нулю, исследуйте самостоятельно.
Пример:
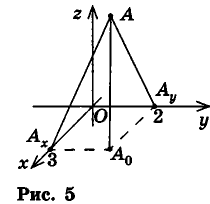
Найдите координаты проекций точки А(3;2;4) на координатные плоскости.
Решение:
Проведем из данной точки перпендикуляр АА0 к плоскости Оху и перпендикуляры ААХ и ААу к осям Ох и Оу соответственно (рис. 5). Найдем координаты точки А0.
Так как 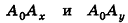
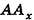
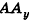
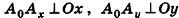
Рассуждая аналогично, определяем, что проекции точки А на плоскости Oxz и Оуz имеют координаты (3;0;4) и (0; 2; 4) соответственно.
- Основные задачи координат
- Движения в пространстве
- Свойства движений в пространстве
- Симметрия в пространстве
- Поворот в пространстве
- Параллельный перенос в пространстве
- Об ориентации поверхности. Лента Мебиуса
- Подобие пространственных фигур
- Преобразование подобия в пространстве
- Гомотетия в пространстве
- Логическое отношение эквивалентности
- Векторы в пространства
- Определение и свойства векторов в пространстве
- Операции над векторами в пространстве
- Векторы
- Операции с векторами
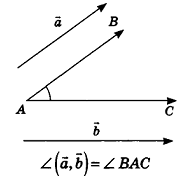
- Скалярное произведение векторов
- Компланарные векторы
- Историческая справка
- Векторы в пространстве и метод координат
- Система координат в пространстве
- Плоскость в пространстве задается уравнением:
- Знакомимся с вектором
- Линейная алгебра
- Что такое вектор
- Как записывать
- Скаляр
- Как изображать
- И зачем нам это всё
- Что дальше
- 📸 Видео
Видео:Собственные векторы и собственные значения матрицыСкачать

Основные задачи координат
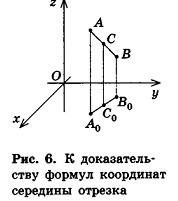
Опираясь на соответствующие свойства координат на плоскости, докажем формулы координат середины отрезка и расстояния между точками в пространстве.
Напомним, что в планиметрии каждая координата середины отрезка равна полусумме соответствующих координат его концов. Такое же свойство сохраняется и в стереометрии. Теорема (формулы координат середины отрезка в пространстве) Координаты середины отрезка вычисляются по формулам:
где 
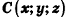
Опустим из точек А, В и С перпендикуляры на плоскость Оху. Основания этих перпендикуляров — точки 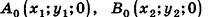
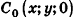
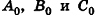
отрезка на плоскости имеем: 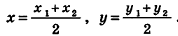
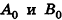
Аналогично, проведя из данных точек перпендикуляры к плоскости 
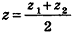
Как известно из курса планиметрии, расстояние между точками 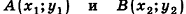
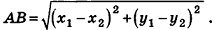
Теорема (формула расстояния между точками в пространстве) Расстояние между точками 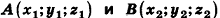
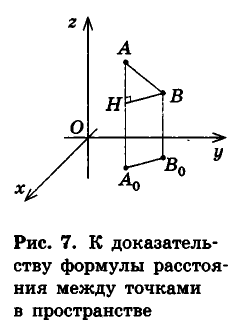
Рассмотрим сначала случай, когда отрезок АВ не параллелен плоскости Оху (рис. 7).
Опустим из точек А и В перпендикуляры 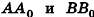
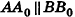
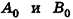
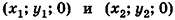
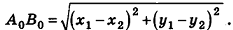
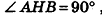
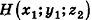
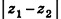
В случае, когда отрезок АВ параллелен оси 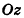
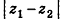
когда отрезок АВ параллелен плоскости Оху, рассмотрите самостоятельно.
Пример:
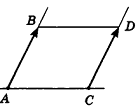
Докажите, что четырехугольник ABCD с вершинами В(4;—3; 2), C(6;3;-4), D (0; 7; -6) является параллелограммом.
Решение:
Найдем координаты середин отрезков АС и BD.
Для отрезка АС:
Для отрезка BD:
Следовательно, отрезки АС и ВD имеют общую середину. Это значит, что прямые АС и BD пересекаются, то есть точки А, В, С и D лежат в одной плоскости. Диагонали четырехугольника ABCD точкой пересечения делятся пополам, таким образом, ABCD — параллелограмм по признаку.
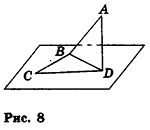
Отметим, что при решении аналогичной задачи в курсе планиметрии мы использовали и другой способ — доказывали попарное равенство противолежащих сторон данного четырехугольника. Но в пространстве этот способ неприемлем, так как из равенств AB = CD и AD = BC не следует, что точки А, В, С и D лежат в одной плоскости. Действительно, четырехугольник ABCD может оказаться пространственным (на рисунке 8 такой четырехугольник получен перегибом параллелограмма ABCD по прямой BD). Очевидно, что в этом случае пространственный четырехугольник ABCD удовлетворяет условиям АВ = CD и AD-ВС, но не является параллелограммом.
Второй способ решения этой задачи будет рассмотрен в § 2.
Пример:
На оси аппликат найдите точку С, равноудаленную от точек А(1;0;3) и В(4;3;-1).
Решение:
Так как искомая точка лежит на оси аппликат, то C(0;0;z). Найдем z, воспользовавшись условием АС = ВС. Имеем: 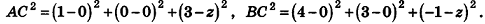
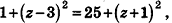
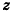
Движения в пространстве
Напомним, что движением на плоскости мы называли геометрическое преобразование, сохраняющее расстояния между точками. Так же определяют движение и в пространстве, причем все свойства движений, известные из курса планиметрии, в стереометрии сохраняются: при движении прямые переходят в прямые, лучи — в лучи, отрезки — в отрезки, и углы между лучами не изменяются.
Свойства движений в пространстве
Новым свойством движения в пространстве является то, что движение переводит плоскость в плоскость.
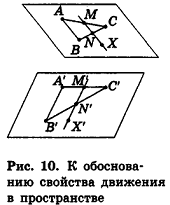
Действительно, пусть точки А, В и С, не лежащие на одной прямой, при движении переходят в точки А’, В’ и С’, также не лежащие на одной прямой (рис. 10). Покажем, что при этом движении плоскость ABC переходит в плоскость А’В’С’. Через произвольную точку X плоскости ABC проведем прямую, пересекающую две стороны треугольника ABC в точках М и N. Очевидно, что при движении эти точки перейдут в точки М’ и N’, лежащие на соответствующих сторонах треугольника А’В’С’. Таким образом, прямая M’N’, в которую переходит прямая MN, принадлежит плоскости А’В’С’, то есть точка Х’ в которую переходит точка X, принадлежит прямой M’N’, а следовательно, и плоскости А’В’С’. Это значит, что произвольная точка плоскости ABC при движении переходит в точку плоскости А’В’С’.
Аналогично можно доказать, что каждую точку плоскости А’В’С’ можно получить из точки плоскости ABC при рассматриваемом движении. Итак, при движении плоскость ABC переходит в плоскость А’В’С’.
Так же как и на плоскости, в пространстве две фигуры называются равными, если они совмещаются движением.
Симметрия в пространстве
Симметрия как один из видов геометрических преобразований знакома вам из курса планиметрии. Преобразования симметрии относительно точки (центральная симметрия) и относительно прямой (осевая симметрия) в пространстве определяют так же, как и на плоскости:
- точки X и X’ называются симметричными относительно точки О, если точка О — середина отрезка XX’ (рис. 11, а); точка О называется центром симметрии;
- точки X иХ’ называются симметричными относительно прямой I, если эта прямая перпендикулярна отрезку XX’ и проходит через его середину (рис. 11, б); прямая I называется осью симметрии.
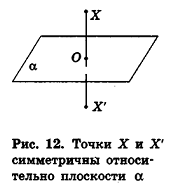
Рассмотрим еще один вид симметрии в пространстве. Пусть а — фиксированная плоскость, X — произвольная точка вне ее. Проведем перпендикуляр ХО к плоскости а и на луче ХО отложим отрезок ОХ’, равный ХО, но лежащий в другом полупространстве относительно плоскости а (рис. 12). Мы получили точку X’, симметричную точке X относительно плоскости а.
Определение:
Точки X и X’ называются симметричными относительно плоскости а, если эта плоскость перпендикулярна отрезку XX’ и проходит через его середину. Точки плоскости а считаются симметричными сами себе.
При этом плоскость а называется плоскостью симметрии.
Очевидно, что точкой, симметричной точке X’ относительно плоскости а, является точка X.
Определение:
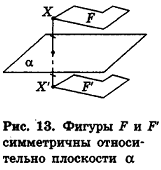
Преобразованием симметрии (симметрией) относительно плоскости а называется такое преобразование фигуры F в фигуру F, при котором каждая точка X фигуры F переходит в точку X’ фигуры F’, симметричную X относительно плоскости а.
При этом фигуры F и F’ называются симметричными относительно плоскости а (рис. 13).
Наглядно представить симметрию относительно плоскости можно с помощью плоского зеркала. Любой объект и его изображение симметричны относительно плоскости зеркала (рис. 14). Поэтому симметрию относительно плоскости иначе называют зеркальной симметрией.
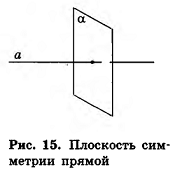
Если преобразование симметрии относительно плоскости а переводит фигуру F в себя, то такая фигура называется симметричной относительно плоскости а, а сама плоскость а — плоскостью симметрии фигуры F. Например, плоскостью симметрии прямой является любая перпендикулярная ей плоскость (рис. 15).
Центры, оси и плоскости симметрии фигуры, если они у нее есть, называются элементами симметрии этой фигуры.
Несложно доказать, что точки, симметричные точке A(x;y;z) относительно координатных плоскостей, осей и начала координат, имеют следующие координаты:
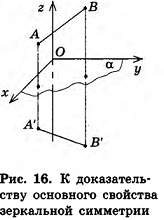
Теорема (основное свойство зеркальной симметрии) Зеркальная симметрия является движением.
Пусть точки А и В при симметрии относительно плоскости а переходят в точки А’ и В’ соответственно. Введем систему координат так, чтобы плоскость Оху совпала с а (рис. 16).

Так как точки, симметричные относительно плоскости Оху, имеют одинаковые абсциссы и ординаты, но противоположные аппликаты, то для точек 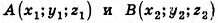
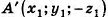
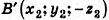
Таким образом, АВ = А’В’. Значит, зеркальная симметрия сохраняет расстояния между точками, то есть является движением.
Из доказанной теоремы следует, что зеркальная симметрия обладает всеми свойствами движения.
Пример №1
Докажите, что если две прямые зеркально симметричны, то они лежат в одной плоскости.
Решение:
Рассмотрим произвольные точки А к В прямой а, которые при зеркальной симметрии относительно плоскости а переходят в точки А’ и В’ прямой а’. По определению симметрии относительно плоскости 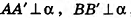
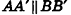
Самые разнообразные виды пространственной симметрии мы наблюдаем в живой и неживой природе, искусстве, технике и т. д. В основе строения живых форм лежит принцип симметрии, причем природа гармонично объединяет различные виды симметрий с почти математической строгостью (рис. 17).
Совершенную симметричную форму имеют природные многогранники — кристаллы (подробнее рассмотрим их в § 12). Физики утверждают, что симметрия является фундаментальным свойством природы, с которым связаны законы сохранения энергии и импульса, строение атомов и молекул, а также особенности природных явлений.
Невозможно переоценить значение симметрии в искусстве. В древнегреческой архитектуре симметрия была воплощением законов целесообразности и гармонии (рис. 18). Идеи зеркальной симметрии широко отражены в живописи Средневековья.
В литературных произведениях существует симметрия образов, ситуаций, мышления. Вспомним хотя бы «закон мести» в греческой трагедии: виновник преступления в конце концов сам становится жертвой такого же преступления.
Яркими примерами симметрии образов являются персонажи комедии Н. В. Гоголя «Ревизор» Добчинский и Бобчинский — сам автор отмечает, что они чрезвычайно похожи друг на друга (рис. 19). Симметричными можно считать и литературные образы героев-антиподов, противостояние между которыми составляет основной конфликт литературного произведения: Шерлок Холмс и профессор Мориарти у А. Конана Дойля, доктор Джекил и мистер Хайд у P. JI. Стивенсона и т. д.
В музыке построение отдельных мелодичных форм также подчиняется законам симметрии. Прослушайте «Рондо-каприччио» великого Бетховена — композитор использует основную тему как своеобразную плоскость симметрии, от которой как бы отражаются отдельные эпизоды и вариации. Симметрия в музыке наглядно проявляется даже через нотную запись (рис. 20).
Глава I. Координаты, векторы и геометрические преобразования в пространстве
Неисчерпаемые возможности симметрии и то широкое применение, которое она получила в разных областях человеческой деятельности, подтверждают универсальность геометрических знаний и значимость геометрии в общечеловеческой культуре.
Поворот в пространстве
Напомним, что на плоскости мы выполняли поворот фигуры вокруг данной точки О в заданном направлении на данный угол. Но в пространстве такое описание поворота не является однозначным: действительно, через фиксированную точку О проходит бесконечно много плоскостей, и в каждой из них поворот фигуры вокруг точки О на данный угол приведет к различным результатам.
Между тем, открывая дверь или переворачивая страницу книги, мы поворачиваем все точки фигуры в одном направлении на определенный угол, причем все точки некоторой прямой остаются неподвижными. Попробуем на основании этих наглядных примеров приблизиться к строгому определению поворота в пространстве.
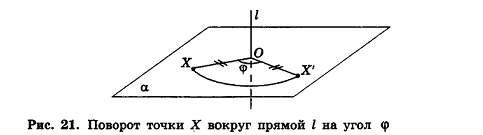
Для этого рассмотрим фиксированную прямую I и произвольную точку X (рис. 21). Проведем через точку X плоскость а, перпендикулярную I, и обозначим точку О пересечения плоскости а с прямой I. В плоскости а выполним поворот точки X вокруг точки О на угол ф, т. е. построим точку X’ так, чтобы 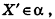
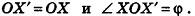
Напомним, что на плоскости мы характеризовали поворот и направлением — по часовой стрелке или против часовой стрелки. В пространстве направление поворота на плоскости а зависит от выбора стороны, с которой мы смотрим на эту плоскость (об этом, в частности, речь будет идти в п. 2.5). Поэтому договоримся считать прямую, вокруг которой выполняется поворот, ориентированной
(т. е. осью с заданным направлением) и рассматривать поворот по часовой стрелке или против часовой стрелки, если смотреть на плоскость с положительного направления этой оси. Например, на рисунке 22 показано направление поворота точек плоскости а вокруг оси I против часовой стрелки.
Поворотом фигуры F вокруг ориентированной прямой I на угол ф называется преобразование фигуры F в фигуру F’, при котором каждая точка X фигуры F (Х&1) переходит в точку X’ фигуры F так, что 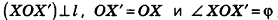
Все углы измеряются по часовой стрелке (или все — против часовой стрелки), точки прямой I при повороте переходят сами в себя.
Иначе говоря, при повороте вокруг ориентированной прямой I каждая точка фигуры F смещается в заданном направлении на данный угол по дуге окружности, плоскость которой перпендикулярна прямой I, центр принадлежит этой прямой, а радиус равен расстоянию от данной точки фигуры F до прямой I. На рисунке 23 фигура F переходит в фигуру F’ при повороте вокруг оси I на угол ф против часовой стрелки.
Прямую I называют осью поворота (или осью вращения), а угол ф — углом поворота.
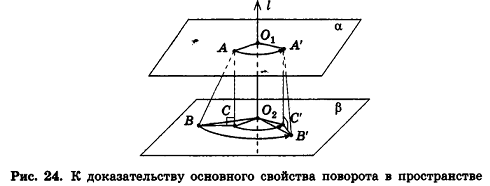
(основное свойство поворота в пространстве) Поворот вокруг прямой является движением.
Пусть при повороте вокруг оси I на угол ф (0° 180° рассмотрите самостоятельно.
Если при повороте вокруг некоторой прямой I фигура F переходит в себя, то говорят, что эта фигура имеет поворотную симметрию (или симметрию вращения). Примеры пространственных фигур, обладающих поворотной симметрией, будут рассмотрены дальше.
Заметим также, что поворот вокруг прямой I на 180° является осевой симметрией относительно прямой I (докажите это самостоятельно).
Параллельный перенос в пространстве
Параллельный перенос в пространстве является разновидностью параллельного проектирования для случая, когда плоскость проектируемой фигуры параллельна плоскости проекции (или совпадает с ней).
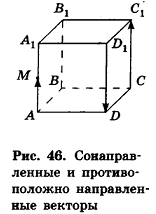
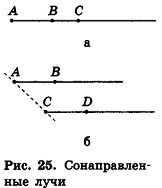
Напомним, что сонаправленными лучами мы называли:
- два луча одной прямой, один из которых является частью другого (например, лучи АС и ВС на рис. 25, а);
- два параллельных луча, лежащих в плоскости по одну сторону от прямой, проходящей через их начальные точки (например, лучи АВ и CD на рис. 25, б).
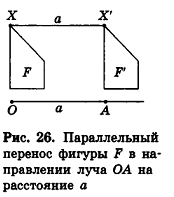
Определение параллельного переноса в стереометрии ничем не отличается от планиметрического. Параллельным переносом, фигуры F в направлении луча OA на расстояние а называется преобразование фигуры F в фигуру F’, при котором каждая точка X фигуры F переходит в точку X’ фигуры F’ так, что лучи XX’ и OA сонаправлены и XX’ = а (рис. 26).
Теорема (основное свойство параллельного переноса в пространстве)
Параллельный перенос в пространстве является движением.
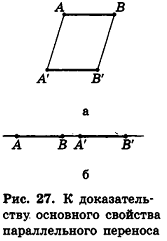
Пусть при параллельном переносе точки А и В переходят в точки А’ и В’ соответственно. Покажем, что АВ = А’В’ Если точки А, В, А’ и В’ не лежат на одной прямой (рис. 27, а), то отрезки АА’ и ВВ’ параллельны и равны. Отсюда АА’В’В — параллелограмм, то есть АВ = А’В’ как противолежащие стороны параллелограмма. В случае, когда точки А, В, А’ и В’ лежат на одной прямой (рис. 27, б), получаем:
В дальнейшем, изучая векторы в пространстве, мы будем рассматривать параллельный перенос на вектор 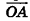
Убедитесь самостоятельно в том, что рассмотренное доказательство справедливо и для других случаев расположения точек А, В, А и В’ на одной прямой.
Параллельный перенос переводит прямую в параллельную прямую (или в себя), отрезок — в равный ему отрезок, угол — в равный ему угол.
Параллельный перенос переводит плоскость в параллельную плоскость (или в себя).
Действительно, поскольку параллельный перенос является движением, то он переводит произвольную плоскость а в плоскость 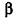
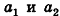
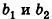
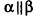
Так же как и на плоскости, в пространстве при условии введения системы координат (рис. 29) параллельный перенос, который переводит точку M(x;y;z) в точку M'(x’;y’;z’), можно задать формулами:
где 
Пример №2
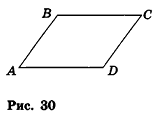
Докажите, что четырехугольник ABCD с вершинами А(-2;1;0), В(4;-3;2), С(б;3;-4), £>(0;7;-б) является параллелограммом.
Решение:
Покажем, что параллельный перенос, который переводит точку В в точку С, переводит точку А в точку D (рис. 30). Сначала найдем формулы этого переноса. Подставив в общие формулы параллельного переноса координаты
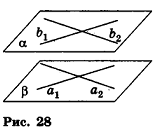
точек В и С, получим уравнения, из которых определим а, b и с: 6 = 4 + а; 3 = -3+b; -4 = 2+ с. Отсюда а = 2; b = 6; с = -6.
Следовательно, искомый перенос задается формулами
Подставив в эти формулы координаты точек А и D, получим правильные равенства: 0 = -2+2, 7 = 1+6, -6=0-6.
Так как по условию ABCD — четырехугольник, его вершины не лежат на одной прямой. Следовательно, по свойству параллельного переноса в четырехугольнике ABCD две стороны параллельны и равны, то есть ABCD — параллелограмм.
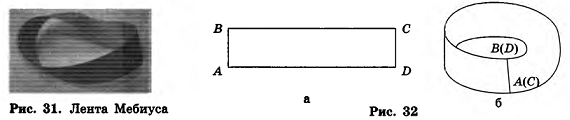
Об ориентации поверхности. Лента Мебиуса
При рассмотрении преобразования поворота было отмечено, что направление поворота в данной плоскости фактически зависит от выбора стороны, с которой мы смотрим на плоскость. Такой выбор стороны называется ориентацией плоскости.
Аналогично можно определить понятие ориентации и для других двусторонних поверхностей в пространстве (поверхности куба, цилиндра, шара и др.). Представим себе, что мы закрасили одну из сторон рассматриваемой поверхности — очевидно, что другая ее сторона останется незакрашенной.
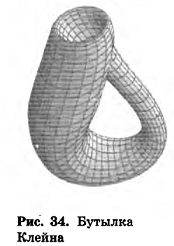
Но эта очевидность только кажущаяся, так как существуют поверхности, которые невозможно ориентировать. Самой простой из них является так называемая лента Мебиуса (рис. 31), открытая в 1858 году немецким астрономом и математиком Августом Мебиусом. Изготовить ее модель очень просто: для этого бумажную ленту, имеющую форму прямоугольника ABCD (рис. 32, а), нужно склеить так, чтобы вершина А совместилась с вершиной С, а вершина В — с вершиной D (рис. 32, б).
Удивительно, но лента Мебиуса является односторонней поверхностью. Чтобы убедиться в этом, попробуйте начать закрашивать ленту с любого места, постепенно перемещаясь по ее поверхности, —
Глава I. Координаты, векторы и геометрические преобразования в пространстве в результате вся поверхность окажется закрашенной. Значит, муравьям, которые ползут по ленте Мебиуса на гравюре М. Эшера (рис. 33), не нужно переползать через край ленты, чтобы попасть на ее «противоположную сторону».
Еще одно интересное свойство ленты Мебиуса заключается в том, что она имеет только один край. Действительно, если выбрать в любом месте края ленты точку и начать от нее двигаться вдоль края, со временем мы вернемся в ту же исходную точку, причем все точки края будут пройдены (проверьте это самостоятельно).
И наконец, предлагаем вам еще один эксперимент: проведите на ленте Мебиуса среднюю линию (т. е. отрезок, который соединяет середины противолежащих сторон АВ и CD прямоугольника, из которого была склеена лента) и попробуйте разрезать по ней ленту. Оказывается, что вместо двух отдельных частей получается дважды перекрученная лента Мебиуса. Невероятно, но это так!
Лента Мебиуса стала первым примером неориентированной поверхности. Позднее были открыты и другие — например, так называемая бутылка Клейна (рис. 34).
Свойство односторонности ленты Мебиуса нашло довольно широкое техническое применение. В XX веке такую ленту использовали для записи звука на непрерывную магнитную пленку, а также как красящую ленту в первых (матричных) принтерах. Ременные передачи или ленты конвейера, имеющие форму ленты Мебиуса, применяют и сегодня, ведь такие ленты служат вдвое дольше, чем обычные, так.как изнашиваются вдвое медленнее (объясните почему). В современной математике существует специальный раздел «топология», в котором рассматриваются, в частности, формы и ориентация поверхностей. А в мировой культуре лента Мебиуса остается символом удивительных открытий, которые до сих пор скрывает геометрия.

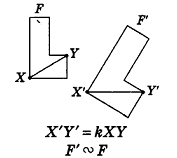
Подобие пространственных фигур
Так же как и на плоскости, преобразование фигуры F в пространстве называется преобразованием подобия, если при этом преобразовании расстояния между точками изменяются в одном и том же отношении. Это значит, что если две произвольные точки X и Y фигуры F при преобразовании подобия переходят в точки X’ и У’ фигуры F’, то X’Y’ = kXY , где k — коэффициент подобия (k > 0).
Преобразование подобия в пространстве
Преобразование подобия в пространстве переводит прямые в прямые, лучи — в лучи, отрезки — в отрезки, а также сохраняет углы между лучами (доказательство этих свойств в стереометрии не отличается от планиметрического). Новым свойством подобия в пространстве является то, что преобразование подобия переводит плоскости в плоскости (докажите это утверждение самостоятельно, аналогично соответствующему обоснованию для движения в п. 2.1).
Две фигуры в пространстве называются подобными, если они переводятся одна в другую преобразованием подобия. Напомним некоторые свойства подобия.
- Любая фигура подобна сама себе:
(рефлексивность подобия).
- Если
(симметричность подобия).
- Если
(транзитивность подобия).
- Отношение площадей подобных фигур равно квадрату коэффициента подобия: если
с коэффициентом k, то
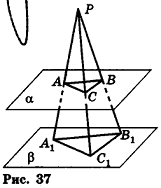
Пример №3
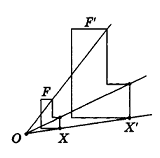
Через точку Р проведены три луча, не принадлежащие одной плоскости и пересекающие параллельные плоскости а и 
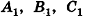
Решение:
Согласно свойству параллельных плоскостей плоскость РАВ пересекает плоскости 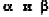
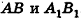
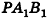
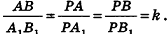
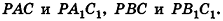
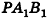
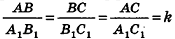
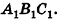
Гомотетия в пространстве
Напомним, что гомотетией с центром в точке О и коэффициентом k>0 называется такое преобразование фигуры F в фигуру F, при котором каждая точка X фигуры F переходит в точку X’ фигуры F’, лежащую на луче ОХ, и ОХ’ = кОХ.
Гомотетия является преобразованием подобия (доказательство этого факта в стереометрии аналогично планиметрическому). Докажем еще одно свойство гомотетии в пространстве.
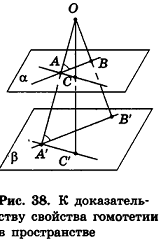
Теорема (свойство гомотетии в пространстве)
Гомотетия переводит плоскость, не проходящую через центр гомотетии, в параллельную плоскость или в себя.
Пусть а — данная плоскость, точка О — центр гомотетии. Рассмотрим случай, когда коэффициент гомотетии h не равен единице (рис. 38).
Данная гомотетия переводит любые точки А и В плоскости а в точки А’ и В’ соответственно, причем 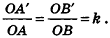
Аналогично, рассматривая в плоскости а прямую АС, пересекающуюся с АВ, можно доказать, что при гомотетии она переходит в параллельную прямую А’С’. Следовательно, при данной гомотетии плоскость а переходит в плоскость а’, содержащую точки А, В’ и С’. Так как А’В’ || АВ и А’С || АС , а плоскости а и а’ не совпадают, то по признаку параллельности плоскостей а’||а.
Очевидно, что в случае k = l плоскость а при гомотетии переходит в себя. Теорема доказана.
Ясно, что плоскость, проходящая через центр гомотетии, при этом преобразовании также переходит в себя.
Обратим внимание и на такой интересный факт (даем его без доказательства): если две фигуры подобны, то одну из них можно получить из другой путем последовательного применения гомотетии и движения.
Пример №4
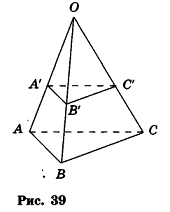
При гомотетии с центром О (2; — 3; 1) треугольник ABC переходит в треугольник А’В’С’. Найдите координаты точек В’ и С’, если А(б;-1;5), А'(4;-2;3), В(0;1;7), С(-4;-5;-7).
Решение:
Найдем длины отрезков OA и OA’:
Так как по определению гомотетии OA’ = kOA, то k = 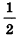
По формулам координат середины отрезка получаем:
Следовательно, B'(l;-1;4), С'(-1;-4-3).
Подобие пространственных фигур находит широкое применение на практике. Например, архитекторы и строители, проектируя размещение новых зданий и сооружений на местности, предлагают заказчикам макеты строящихся объектов (рис. 40).
Логическое отношение эквивалентности
Как мы уже отмечали, отношение подобия на множестве геометрических фигур является рефлексивным, симметричным и транзитивным. Эти три свойства присущи и некоторым другим отношениям, причем не только геометрическим.
Например, для любых двух натуральных чисел а и b можно рассматривать отношение «число а дает при делении на 5 тот же остаток, что и число Ь» (обоснуйте самостоятельно рефлексивность, симметричность и транзитивность такого отношения). На множестве людей указанные свойства имеет отношение «а является гражданином той же страны, что и b» (если не принимать во внимание людей без гражданства и людей с двойным гражданством), а на множестве слов русского языка — отношение «слово а имеет тот же корень, что и слово b.
В логике отношения, имеющие свойства рефлексивности, симметричности и транзитивности, называют отношениями эквивалентности. Наличие такого отношения на множестве однородных предметов позволяет разделить их на классы эквивалентности — подмножества, элементы которых имеют общие свойства. Например, отношение подобия на множестве многоугольников позволяет нам рассматривать как отдельные классы равносторонние треугольники, квадраты и т. д. Действительно, все фигуры одного класса имеют общие геометрические свойства, которые сохраняются при преобразовании подобия. О таких фигурах. говорят, что они являются равными с точностью до подобия (другими словами, имеют одинаковую форму, но отличаются размерами). Для изучения геометрических свойств фигур определенного класса достаточно рассмотреть одну произвольную фигуру и на ее примере исследовать особенности остальных фигур данного класса.
Деление на классы эквивалентности используют не только математики. Так, филологи, рассматривая для существительных русского языка отношение «слова а и b имеют одинаковые окончания при склонении», делят все существительные на три склонения. Идея деления на классы эквивалентности лежит в основе многих химических и биологических классификаций. Вспомните, как использовал эту идею в периодической таблице химических элементов Д. И. Менделеев.
Векторы в пространства
Большинство понятий и утверждений для векторов непосредственно переносятся в стереометрию из планиметрии. Напомним основные положения соответствующей геометрической теории, подробно останавливаясь на тех из них, которые в пространстве выглядят иначе, чем на плоскости.
Определение и свойства векторов в пространстве
Как известно из курса геометрии 9 класса, вектором, называется направленный отрезок. Направление вектора (от начала к концу) на рисунках обозначают стрелкой. Вектор, начало и конец которого совпадают, называется нулевым. Нулевой вектор не имеет какого-либо определенного направления. На рисунке 44 изображены ненулевые векторы 
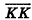
Нулевой вектор часто обозначают 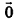
Так же как и на плоскости, ненулевой вектор в пространстве характеризуется не только направлением, но и длиной. Это позволяет рассматривать параллельный перенос в направлении луча АВ на расстояние, равное длине отрезка АВ, как параллельный перенос на вектор 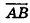
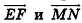
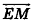
Так как положение точки в пространстве задается тремя координатами, дополняется определение координат вектора.
Определение:
Координатами вектора 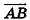
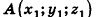
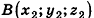
Соответственно длина (модуль) вектора 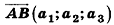
Нулевой вектор имеет нулевые координаты, и его длина равна нулю:
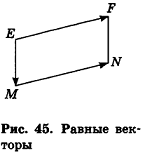
Так же как и на плоскости, в пространстве равные векторы имеют равные координаты, и наоборот: если у векторов соответствующие координаты равны, то эти векторы равны.
Напомним, что ненулевые векторы называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Нулевой вектор считается коллинеарным любому вектору.
В свою очередь, среди коллинеарных векторов различают сонаправленные и противоположно направленные. Если лучи АВ и CD сонаправлены, то ненулевые векторы 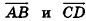
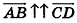
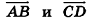
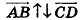
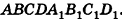
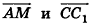
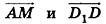
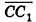
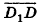
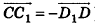
Пример №5
Даны точки А (-7; 4; 2) и В(-2;0;-l). Найдите координаты кондов вектора 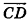
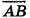
Решение:
Пусть 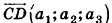
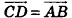
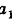
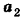
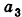
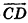
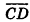
Операции над векторами в пространстве
Операции сложения и вычитания для векторов в пространстве определяют аналогично тому, как их вводили на плоскости. Итак, для векторов 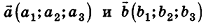
Так же сохраняются в пространстве и соответствующие свойства этих операций. Для любых векторов 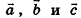
Доказательство утверждений 1-4 несложно получить с помощью геометрических построений аналогично тому, как это проводилось на плоскости.
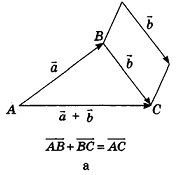
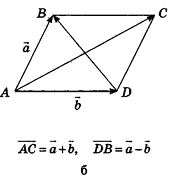
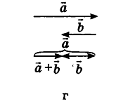
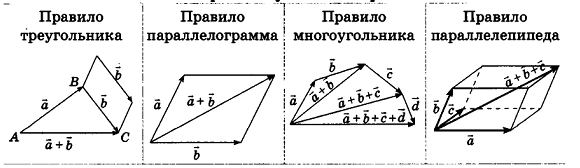
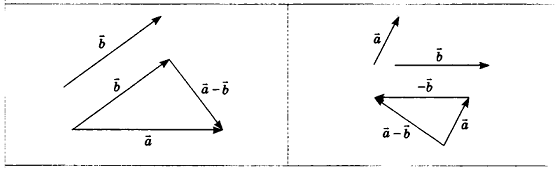
Для действий с неколлинеарными векторами в геометрической форме в пространстве, как и на плоскости, можно воспользоваться правилом треугольника (рис. 47, а) и правилом параллелограмма (рис. 47, б). Правила сложения двух коллинеарных векторов иллюстрирует рисунок 47, в, г.
Обобщением правила треугольника для сложения нескольких векторов является правило многоугольника (рис. 48, а). Особенность его применения в пространстве заключается в том, что векторы-слагаемые не обязательно принадлежат одной плоскости (то есть многоугольник, который получается при построении вектора-суммы, может быть пространственным). Например, на рисунке 48, б в тетраэдре РАВС получим векторное равенство
Опишем еще одно правило, которое служит для. сложения трех векторов в пространстве. Пусть векторы-слагаемые 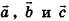
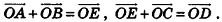
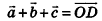
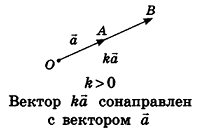
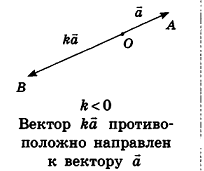
Произведением вектора 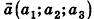
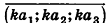
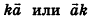
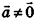
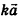
Преобразование подобия переводит прямые в прямые, отрезки — в отрезки, плоскости — в плоскости, а также сохраняет углы между лучами X’Y’ = kXY
Гомотетией с центром в точке О и коэффициентом k (k>0) называется такое преобразование фигуры F в фигуру F’, при котором каждая точка X фигуры F переходит в точку X’ фигуры F, лежащую на луче ОХ, и ОХ’ = кОХ
Число k называют коэффициентом гомотетии, а фигуры F и F’ — гомотетичными
Основное свойство гомотетии: гомотетия является преобразованием подобия
Гомотетия переводит плоскость, не проходящую через центр гомотетии, в параллельную плоскость или в себя
Векторы
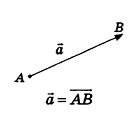
Вектором называется направленный отрезок
Координатами вектора с началом в точке 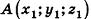
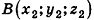
Длина (модуль) вектора 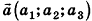
Ненулевые векторы называются коллинеарными, если они лежат на одной прямой или на параллельных прямых
Векторы 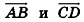
Векторы 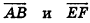
Противоположными векторами называются два противоположно направленных вектора одинаковой длины
Два вектора называются равными, если они совмещаются параллельным переносом
От любой точки можно отложить вектор, равный данному, и притом только один Критерии равных векторов:
- векторы сонаправлены и имеют равные длины;
- векторы имеют равные координаты
Операции с векторами
Сложение векторов
Суммой векторов 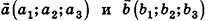
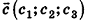
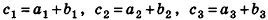
Построение суммы векторов
Вычитание векторов
Разностью векторов 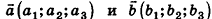
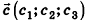
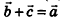
Построение разности векторов
Умножение вектора на число
Произведением вектора 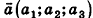
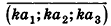
Если 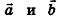
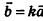
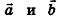
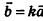
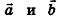
У коллинеарных векторов соответствующие координаты пропорциональны, и наоборот: если у двух векторов соответствующие координаты пропорциональны, то эти векторы коллинеарны
Скалярное произведение векторов
Скалярным произведением векторов 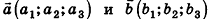
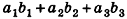
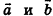
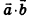
Скалярное произведение 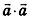
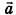
Скалярное произведение векторов равно произведению их длин на косинус угла между ними:
Свойство и признак перпендикулярных векторов: если 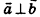
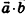
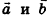
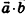
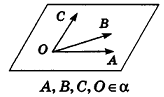
Компланарные векторы
Ненулевые векторы называются компланарными, если при откладывании их от одной и той же точки они лежат в одной плоскости
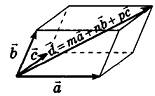
Любой вектор d можно разложить по трем некомпланарным векторам 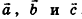
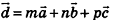
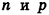
Историческая справка
Эпоха великих географических открытий и обусловленное ими развитие производства, торговли, мореплавания стали толчком к возникновению аналитической геометрии. Этот раздел геометрии, основанный на введении прямоугольных координат и установлении соответствия между алгебраическими уравнениями и геометрическими фигурами, стал итогом многолетних математических исследований.
Создателями аналитической геометрии считают французских ученых Рене Декарта (1696-1650) и Пьера Ферма (1601-1665). Ферма в начале XVII века, занимаясь восстановлением утраченных работ древнегреческих ученых, в частности Аполлония Пергского, определил общий подход к изучению геометрических мест точек через алгебраические уравнения. Открытие Декартом системы координат на плоскости позволило создать математический аппарат для воплощения идей аналитической геометрии. Но как Ферма, так и Декарт только говорили о возможности использования координат в пространстве. Трехмерную систему координат первым начал применять французский математик Алексис Клод Клеро (1713-1765), а систематическое изложение аналитической геометрии в пространстве представил в 1748 году выдающийся ученый Леонард Эйлер.
В историю аналитической геометрии вписаны также имена украинских ученых. Уроженец Винни-чины Виктор Яковлевич Буняковский (1804-1889) учился математике в Париже, у ведущих ученых своего времени — Коши, Лежандра, Пуассона, Лапласа, а позднее работал в Петербурге. Он был автором около ста работ по математическому анализу, алгебре, геометрии, теории чисел и теории вероятностей. Так, известное вам неравенство а-6
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Собственные значения и собственные векторы матрицы (4)Скачать

Векторы в пространстве и метод координат
Существует два способа решения задач по стереометрии
Первый — классический — требует отличного знания аксиом и теорем стереометрии, логики, умения построить чертеж и свести объемную задачу к планиметрической. Способ хорош тем, что развивает мозги и пространственное воображение.
Другой метод — применение векторов и координат. Это простые формулы, алгоритмы и правила. Он очень удобен, особенно когда времени до экзамена мало, а решить задачу хочется.
Если вы освоили векторы на плоскости и действия с ними — то и с векторами в пространстве разберетесь. Многие понятия окажутся знакомыми.
Видео:Уроки Figma | Симметричный векторСкачать

Система координат в пространстве
Выберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.
Получилась система координат в трехмерном пространстве. Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2.
Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:
Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.

Длина вектора в пространстве – это расстояние между точками A и B. Находится как корень квадратный из суммы квадратов координат вектора.
Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:
Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма
Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости. Только координат не две, а три. Возьмем векторы и
.
Произведение вектора на число:
Скалярное произведение векторов:
Косинус угла между векторами:
Последняя формула удобна для нахождения угла между прямыми в пространстве. Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.
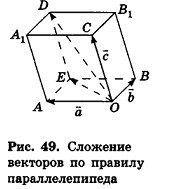
1. В кубе ABCDA1B1C1D1 точки E и K — середины ребер соответственно A1B1 и B1C1. Найдите косинус угла между прямыми AE и BK.
Если вам достался куб — значит, повезло. Он отлично вписывается в прямоугольную систему координат. Строим чертеж:
Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому возьмем единичный куб, все ребра которого равны 1.
Прямые AE и BK — скрещиваются. Найдем угол между векторами и
. Для этого нужны их координаты.
Запишем координаты векторов:
и найдем косинус угла между векторами и
:
2. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, K — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BK.
Лучше всего выбрать начало координат в центре основания пирамиды, а оси X и Y сделать параллельными сторонам основания.
Координаты точек A, B и C найти легко:
Из прямоугольного треугольника AOS найдем
Координаты вершины пирамиды:
Точка E — середина SB, а K — середина SC. Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.
Найдем координаты векторов и
и угол между ними:
Покажем теперь, как вписать систему координат в треугольную призму:
3. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, точка D — середина ребра A1B1. Найдите косинус угла между прямыми AD и BC1
Пусть точка A — начало координат. Возьмем ось X параллельно стороне BC, а ось Y перпендикулярно ей. Другими словами, на оси Y будет лежать отрезок AH, являющийся высотой треугольника ABC. Нарисуем отдельно нижнее основание призмы.
Запишем координаты точек:
Точка D — середина A1B1. Значит, пользуемся формулами для координат середины
отрезка.
Найдем координаты векторов и
, а затем угол между ними:
Смотрите, как легко с помощью векторов и координат найти угол между прямыми. А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.
Видео:А.7.40 Метод Якоби поиска собственных векторов и значений симметричных матрицСкачать

Плоскость в пространстве задается уравнением:
Здесь числа A, B и C — координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.
Вместо x, y и z можно подставить в уравнение координаты любой точки, принадлежащей данной плоскости. Получится верное равенство.
Плоскость в пространстве можно провести через любые три точки, не лежащие на одной прямой. Поэтому для того, чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.
Покажем, как это делается.
Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; −2; 0) и K (4; 1; 2).
Уравнение плоскости выглядит так:
Подставим в него по очереди координаты точек M, N и K.
То есть A + C + D = 0.
Аналогично для точки K:
Получили систему из трех уравнений:
В ней четыре неизвестных: A, B, C и D. Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило простое — вместо одной из переменных можно взять любое число, не равное нулю.
Пусть, например, D = −2. Тогда:
Выразим C и B через A и подставим в третье уравнение:
Решив систему, получим:
Уравнение плоскости MNK имеет вид:
Умножим обе части уравнения на −3. Тогда коэффициенты станут целыми:
Вектор — это нормаль к плоскости MNK.
Уравнение плоскости, проходящей через заданную точку имеет вид:
Угол между плоскостями равен углу между нормалями к этим плоскостям:
Не правда ли, знакомая формула? Скалярное произведение нормалей поделили на произведение их длин.
Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла.
Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.
4. В кубе ABCDA1B1C1D1 точки E и F — середины ребер соответственно A1B1 и A1D1. Найдите тангенс угла между плоскостями AEF и BDD1.
Строим чертеж. Видно, что плоскости AEF и BDD1 пересекаются где-то вне куба. В классическом решении пришлось бы строить линию их пересечения. Но векторно-координатный метод значительно всё упрощает. Не будем ломать голову над тем, по какой прямой пересекаются плоскости. Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD1.
Сначала — нормаль к плоскости BDD1. Конечно, мы можем подставить координаты точек B, D и D1 в уравнение плоскости и найти коэффициенты, которые и будут координатами вектора нормали. А можем сделать хитрее — увидеть нужную нормаль прямо на чертеже. Ведь плоскость BDD1 — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.
Итак, первый вектор нормали у нас уже есть:
Напишем уравнение плоскости AEF.
Берем уравнение плоскости и по очереди подставляем в него, вместо x, y и z, соответствующие координаты точек A, E и F.
Пусть С = -1. Тогда A = B = 2.
Уравнение плоскости AEF:
Нормаль к плоскости AEF:
Найдем угол между плоскостями:
5. Основание прямой четырехугольной призмы BCDA1B1C1D1 — прямоугольник ABCD, в котором AB = 5, AD = √33. Найдите тангенс угла между плоскостью грани AA1D1D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B1D, если расстояние между прямыми A1C1 и BD равно √3.
Эта задача наглядно показывает, насколько векторный метод проще классического. Попробуйте, для разнообразия, построить необходимые сечения и провести все доказательства — как это делается в «классике» 🙂
Строим чертеж. Прямую четырехугольную призму можно по-другому назвать «параллелепипед».
Замечаем, что длина и ширина параллелепипеда у нас есть, а вот высота — вроде не дана. Как же ее найти?
«Расстояние между прямыми A1C1 и BD равно √3». Прямые A1C1 и BD скрещиваются. Одна из них — диагональ верхнего основания, другая — диагональ нижнего. Вспомним, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общий перпендикуляр к A1C1 и BD — это, очевидно, OO1, где O — точка пересечения диагоналей нижнего основания, O1 — точка пересечения диагоналей верхнего. А отрезок OO1 и равен высоте параллелепипеда.
Плоскость AA1 D1 D — это задняя грань призмы на нашем чертеже. Нормаль к ней — это любой вектор, перпендикулярный задней грани, например, вектор или, еще проще, вектор
.
Осталась еще «плоскость, проходящая через середину ребра CD перпендикулярно прямой B1D». Но позвольте, если плоскость перпендикулярна прямой B1D — значит, B1D и есть нормаль к этой плоскости! Координаты точек B1 и D известны:
Координаты вектора — тоже:
Находим угол между плоскостями, равный углу между нормалями к ним:
Зная косинус угла, находим его тангенс по формуле
Получим:
Ответ:
Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов.
Пусть — вектор, лежащий на прямой m (или параллельный ей),
— нормаль к плоскости α.
Находим синус угла между прямой m и плоскостью α по формуле:
6. В кубе ABCDA1B1C1D1 точка E — середина ребра A1B1. Найдите синус угла между прямой AE и плоскостью BDD1.
Как всегда, рисуем чертеж и выбираем систему координат
Находим координаты вектора .
Нужно ли нам уравнение плоскости BDD1? В общем-то, без него можно обойтись. Ведь эта плоскость является диагональным сечением куба, а значит, нормалью к ней будет любой вектор, ей перпендикулярный. Например, вектор .
Найдем угол между прямой и плоскостью:
Ответ:
Расстояние от точки M с координатами x0, y0 и z0 до плоскости α, заданной уравнением Ax + By + Cz + D = 0, можно найти по формуле:
7. В основании прямоугольного параллелепипеда BCDA1B1C1D1 лежит прямоугольник ABCD со сторонами AB = , AD =
. Высота параллелепипеда AA1 =
. Найдите расстояние от точки A до плоскости A1DB.
Построим чертеж и выпишем координаты точек:
Запишем уравнение плоскости A1DB. Вы помните, как это делается — по очереди подставляем координаты точек A1, D и B в уравнение Ax + Be + Cz + D
Решим эту систему. Выберем
Тогда
Уравнение плоскости A1DB имеет вид:
Дальше все просто. Находим расстояние от точки A до плоскости A1DB:
В некоторых задачах по стереометрии требуется найти расстояние от прямой до параллельной ей плоскости. В этом случае можно выбрать любую точку, принадлежащую данной прямой.
Видео:Собственные векторы и собственные числа линейного оператораСкачать

Знакомимся с вектором
Основы линейной алгебры для тех, кого это миновало в универе.
Вы наверняка слышали много историй о программистах, которые учились в технических вузах, изучали высшую математику и теперь пользуются этими знаниями в программировании. И если кого-то это не коснулось, может быть ощущение, что он пропустил в жизни что-то важное.
Будем это исправлять. Попробуем разобрать некоторые базовые понятия из математики за пределами школьной программы. И заодно покажем, как оно связано с программированием и для каких задач полезно.
⚠️ Математики, помогайте. Мы тут многое упростили, поэтому будем рады увидеть ваши уточнения и замечания в комментариях.
Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Линейная алгебра
Есть математика: она изучает абстрактные объекты и их взаимосвязи. Благодаря математике мы знаем, что если сложить два объекта с ещё двумя такими же объектами, то получится четыре объекта. И неважно, что это были за объекты: яблоки, козы или ракеты. Математика берёт наш вещественный мир и изучает его более абстрактные свойства.
Внутри математики есть алгебра: если совсем примитивно, то в алгебре мы вместо чисел начинаем подставлять буквы и изучать ещё более абстрактные свойства объектов.
Например, мы знаем, что если a + b = c , то a = c − b . Мы не знаем, что стоит на местах a, b или c, но для нас это такой абстрактный закон, который подтверждается практикой.
Внутри алгебры есть линейная алгебра — она изучает векторы, векторные пространства и другие абстрактные понятия, которые в целом относятся к некой упорядоченной информации. Например, координаты ракеты в космосе, биржевые котировки, расположение пикселей в изображении — всё это примеры упорядоченной информации, которую можно описывать векторами. И вот их изучает линейная алгебра.
В программировании линейная алгебра нужна в дата-сайенс, где из упорядоченной информации создаются алгоритмы машинного обучения.
Если представить линейную алгебру в виде дома, то вектор — это кирпич, из которого всё состоит. Сегодня разберёмся, что такое вектор и как его понимать.
Видео:Как разложить вектор по базису - bezbotvyСкачать

Что такое вектор
Вы наверняка помните вектор из школьной программы — это такая стрелочка. Она направлена в пространство и измеряется двумя параметрами: длиной и направлением. Пока длина и направление не меняются, вектор может перемещаться в пространстве.
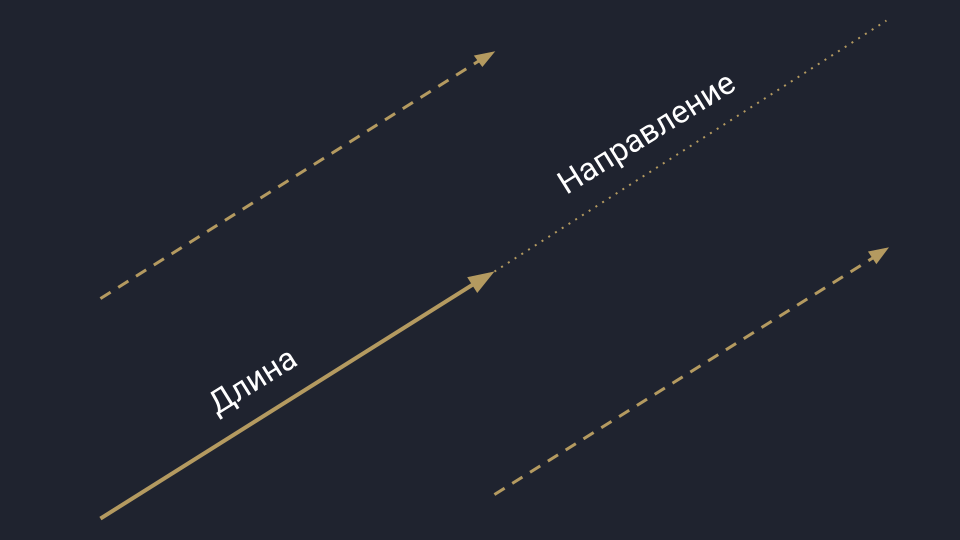
У аналитиков вектор представляется в виде упорядоченного списка чисел: это может быть любая информация, которую можно измерить и последовательно записать. Для примера возьмём рынок недвижимости, который нужно проанализировать по площади и цене домов — получаем вектор, где первая цифра отвечает за площадь, а вторая — за цену. Аналогично можно сортировать любые данные.
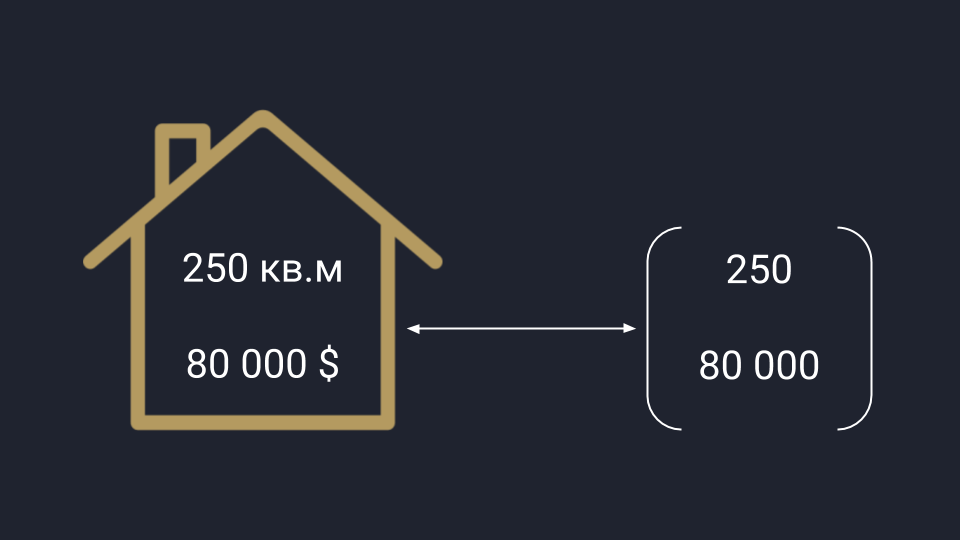
Математики обобщают оба подхода и считают вектор одновременно стрелкой и числом — это связанные понятия, перетекающие друг в друга в зависимости от задачи. В одних случаях удобней считать, а в других — показать всё графически. В обоих случаях перед нами вектор.
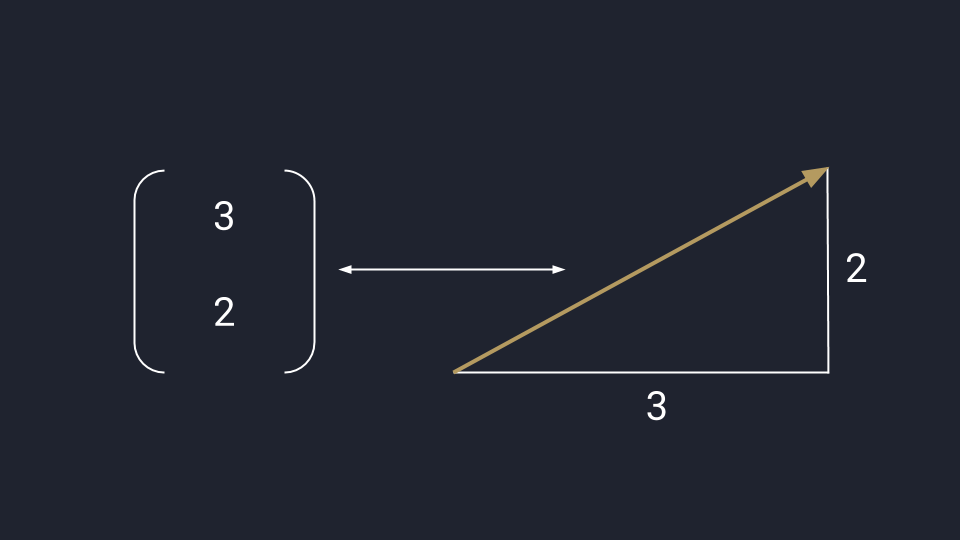
В дата-сайенс используется математическое представление вектора — программист может обработать данные и визуализировать результат. В отличие от физического представления, стрелки векторов в математике привязаны к системе координат Х и У — они не блуждают в пространстве, а исходят из нулевой точки.
👉 Получается, вектор – это такой способ записывать, хранить и обрабатывать не одно число, а какое-то организованное множество чисел. Благодаря векторам мы можем представить это множество как единый объект и изучать его взаимодействие с другими объектами.
Например, можно взять много векторов с ценами на недвижимость, как-то их проанализировать, усреднить и обучить на них алгоритм. Без векторов это были бы просто «рассыпанные» данные, а с векторами — порядок.
Видео:Нахождение точки, симметричной данной относительно плоскости в пространствеСкачать

Как записывать
Вектор можно записать в строку или в столбец. Для строчной записи вектор обозначают одной буквой, ставят над ней черту, открывают круглые скобки и через запятую записывают координаты вектора. Для записи в столбец координаты вектора нужно взять в круглые или квадратные скобки — допустим любой вариант.
Строгий порядок записи делает так, что каждый набор чисел создаёт только один вектор, а каждый вектор ассоциируется только с одним набором чисел. Это значит, что если у нас есть координаты вектора, то мы их не сможем перепутать.
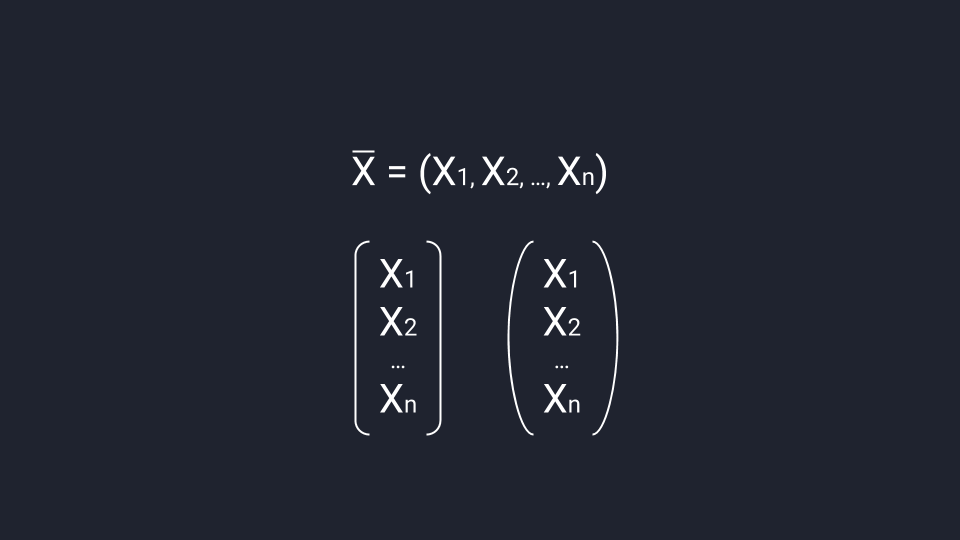
Скаляр
Помимо понятия вектора есть понятие скаляра. Скаляр — это просто одно число. Можно сказать, что скаляр — это вектор, который состоит из одной координаты.
Помните физику? Есть скалярные величины и есть векторные. Скалярные как бы описывают просто состояние, например, температуру. Векторные величины ещё и описывают направление.
Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

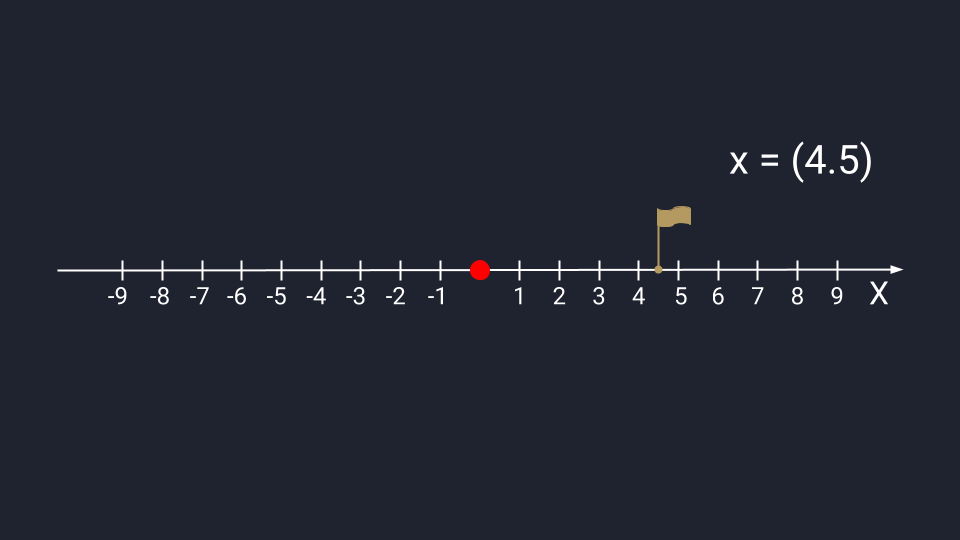
Как изображать
Вектор из одного числа (скаляр) отображается в виде точки на числовой прямой.
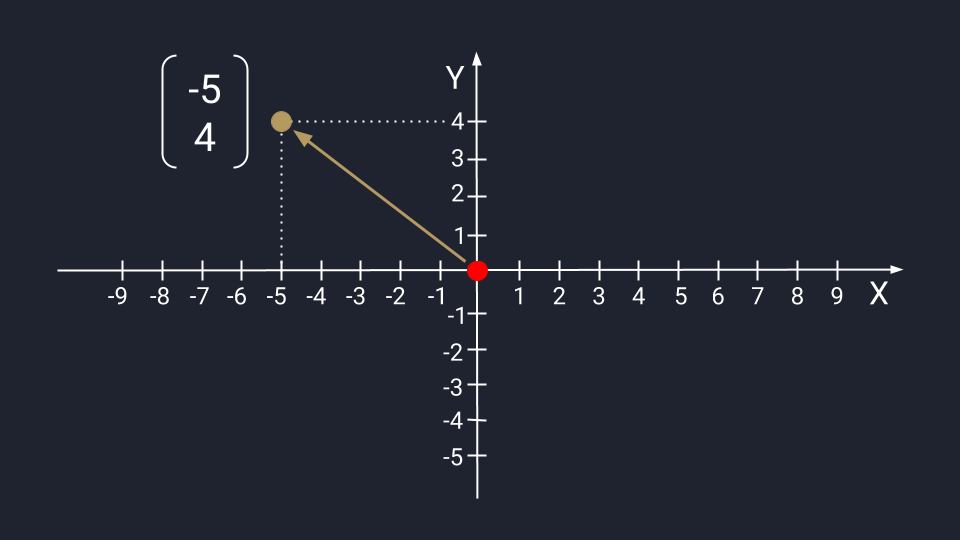
Вектор из двух чисел отображается в виде точки на плоскости осей Х и Y. Числа задают координаты вектора в пространстве — это такая инструкция, по которой нужно перемещаться от хвоста к стрелке вектора. Первое число показывает расстояние, которое нужно пройти вдоль оси Х; второе — расстояние по оси Y. Положительные числа на оси Х обозначают движение вправо; отрицательные — влево. Положительные числа на оси Y — идём вверх; отрицательные — вниз.
Представим вектор с числами −5 и 4. Для поиска нужной точки нам необходимо пройти влево пять шагов по оси Х, а затем подняться на четыре этажа по оси Y.
Вектор из трёх чисел отображается в виде точки на плоскости осей Х, Y и Z. Ось Z проводится перпендикулярно осям Х и У — это трёхмерное измерение, где вектор с упорядоченным триплетом чисел: первые два числа указывают на движение по осям Х и У, третье — куда нужно двигаться вдоль оси Z. Каждый триплет создаёт уникальный вектор в пространстве, а у каждого вектора есть только один триплет.
Если вектор состоит из четырёх и более чисел, то в теории он строится по похожему принципу: вы берёте координаты, строите N-мерное пространство и находите нужную точку. Это сложно представить и для обучения не понадобится.
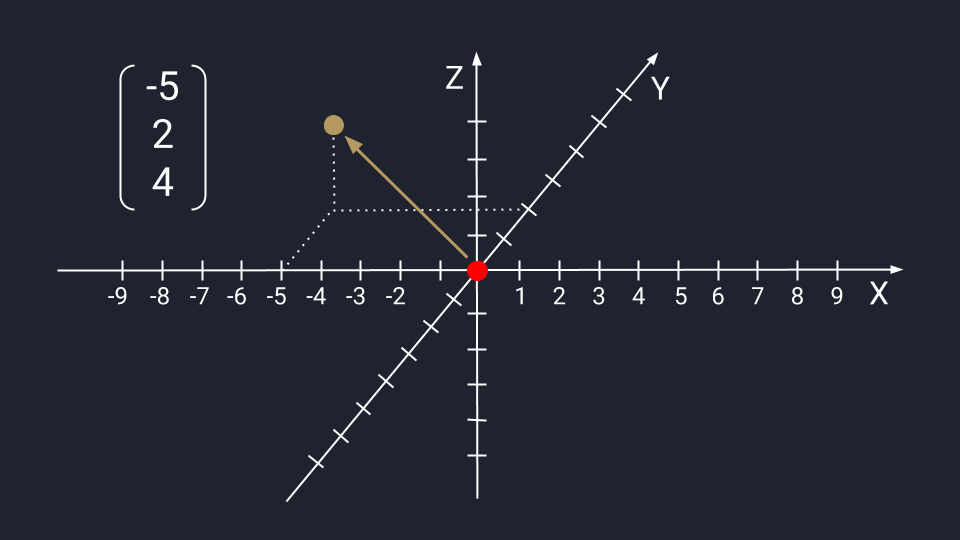
Помните, что все эти записи и изображения с точки зрения алгебры не имеют отношения к нашему реальному трёхмерному пространству. Вектор — это просто какое-то количество абстрактных чисел, собранных в строгом порядке. Вектору неважно, сколько там чисел и как их изображают люди. Мы же их изображаем просто для наглядности и удобства.
Например, в векторе спокойно может быть 99 координат. Для его изображения нам понадобилось бы 99 измерений, что очень проблематично на бумаге. Но с точки зрения вектора это не проблема: перемножать и складывать векторы из двух координат можно так же, как и векторы из 9999999 координат, принципы те же.
Видео:Орт вектора. Нормировать вектор. Найти единичный векторСкачать

И зачем нам это всё
Вектор — это «кирпичик», из которого строится дата-сайенс и машинное обучение. Например:
- На основании векторов получаются матрицы. Если вектор — это как бы линия, то матрица — это как бы плоскость или таблица.
- Машинное обучение в своей основе — это перемножение матриц. У тебя есть матрица с данными, которые машина знает сейчас; и тебе нужно эту матрицу «дообучить». Ты умножаешь существующую матрицу на какую-то другую матрицу и получаешь новую матрицу. Делаешь так много раз по определённым законам, и у тебя обученная модель, которую на бытовом языке называют искусственным интеллектом.
Кроме того, векторы используются в компьютерной графике, работе со звуком, инженерном и просто любом вычислительном софте.
И давайте помнить, что вектор — это не какая-то сложная абстрактная штука, а просто сумка, в которой лежат числа в определённом порядке. То, что мы называем это вектором, — просто нюанс терминологии.
Видео:Собственные значения и собственные векторыСкачать

Что дальше
В следующий раз разберём операции с векторами. Пока мы готовим материал — рекомендуем почитать интервью с Анастасией Никулиной. Анастасия ведёт ютуб-канал по дата-сайнс и работает сеньором дата-сайентистом в Росбанке.
📸 Видео
Координаты вектора. 9 класс.Скачать

§7 Направляющие косинусы вектораСкачать

Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать

Найдите разложение вектора по векторам (базису)Скачать

Как построить точки в системе координат OXYZСкачать

Единичный векторСкачать

Поступающим в магистратуру МГУ, математика, 2018 год, первая волна, задача 1 (1)Скачать

Как найти точку, симметричную точке А(3;4) относительно начала координат. Как решать. Простой способСкачать

Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисеСкачать

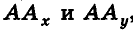
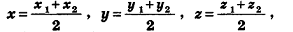
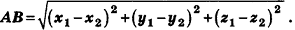
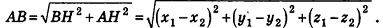
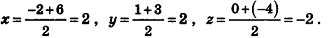
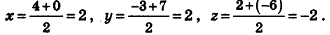

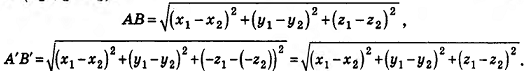




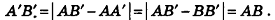
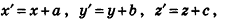
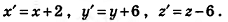

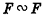 (рефлексивность подобия).
(рефлексивность подобия).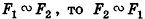 (симметричность подобия).
(симметричность подобия).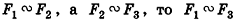 (транзитивность подобия).
(транзитивность подобия).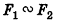 с коэффициентом k, то
с коэффициентом k, то