В этой небольшой статье, будут рассмотрены основные виды сопряжений и Вы узнаете о том, как построить сопряжение углов, прямых линий, окружностей и дуг, окружностей с прямой.
Сопряжением называют плавный переход одной линии в другую. Для того чтобы построить сопряжение, нужно найти центр сопряжения и точки сопряжений.
Точка сопряжения – это общая точка для сопрягаемых линий. Точку сопряжения также называют точкой перехода.
Ниже будут рассмотрены основные типы сопряжений.
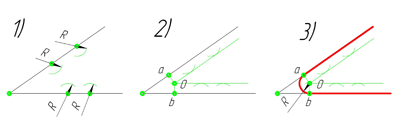
- Сопряжение углов (Сопряжение пересекающихся прямых)
- Сопряжение прямого угла(Сопряжение пересекающихся прямых под прямым углом)
- Сопряжение острого угла(Сопряжение пересекающихся прямых под острым углом)
- Сопряжение тупого угла(Сопряжение пересекающихся прямых под тупым углом)
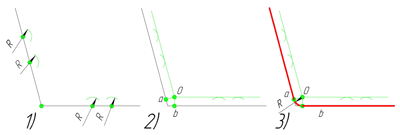
- Сопряжение параллельных прямых линий
- Сопряжение окружностей(дуг) с прямой линией
- Внешнее сопряжение дуги и прямой линии
- Внутреннее сопряжение прямой линии с дугой
- Сопряжение окружностей (дуг)
- Внешнее сопряжение дуг окружностей
- Внутреннее сопряжение дуг окружностей
- Смешанное сопряжение дуг окружностей
- Урок черчения в 7 классе «Построение сопряжений»
- «Управление общеобразовательной организацией: новые тенденции и современные технологии»
- Дистанционное обучение как современный формат преподавания
- Современные методы арт-терапии: базовые техники
- Правополушарная живопись
- Оставьте свой комментарий
- Подарочные сертификаты
- Урок черчения в 7-м классе по теме «Сопряжения»
- 🌟 Видео
Видео:Черчение. Внутреннее, внешнее и смешенное сопряжение двух окружностей.Скачать

Сопряжение углов (Сопряжение пересекающихся прямых)
Сопряжение прямого угла(Сопряжение пересекающихся прямых под прямым углом)
В данном примере будет рассмотрено построение сопряжения прямого угла заданным радиусом сопряжения R. Первым делом найдём точки сопряжения. Для нахождения точек сопряжения, нужно поставить циркуль в вершину прямого угла и провести дугу радиусом R до пересечения со сторонами угла. Полученные точки и будут являться точками сопряжения. Далее нужно найти центр сопряжения. Центром сопряжения будет точка равноудалённая от сторон угла. Проведём из точек a и b две дуги радиусом сопряжения R до пересечения друг с другом. Полученная на пересечении точка О и будет центром сопряжения. Теперь из центра сопряжения точки О описываем дугу радиусом сопряжения R от точки a до точки b. Сопряжение прямого угла построено.
Сопряжение острого угла(Сопряжение пересекающихся прямых под острым углом)
Ещё один пример сопряжения угла. В этом примере будет построено сопряжение
острого угла. Для построения сопряжения острого угла раствором циркуля,равным радиусу сопряжения R, проведём из двух произвольных точек на каждой стороне угла по две дуги. Затем проведём касательные к дугам до пересечения в точке О, центре сопряжения. Из полученного центра сопряжения опустим перпендикуляр к каждой из сторон угла. Так мы получим точки сопряжения a и b. Затем проведём из центра сопряжения, точки О, дугу радиусом сопряжения R, соединив точки сопряжения a
и b. Сопряжение острого угла построено.
Сопряжение тупого угла(Сопряжение пересекающихся прямых под тупым углом)
Сопряжение тупого угла строится по аналогии с сопряжением острого угла. Мы также, сначала радиусом сопряжения R проводим по две дуги из двух произвольно взятых точек на каждой из сторон, а затем проводим касательные к этим дугам до пересечения в точке О, центре сопряжения. Затем опускаем перпендикуляры из центра сопряжения к каждой из сторон и соединяем дугой, равной радиусу сопряжения тупого угла R, полученные точки a и b.
Видео:1 2 4 сопряжение окружностейСкачать

Сопряжение параллельных прямых линий
Построим сопряжение двух параллельных прямых. Нам задана точка сопряжения a, лежащая на одной прямой. Из точки a проведём перпендикуляр до пересечения его с другой прямой в точке b. Точки a и b являются точками сопряжения прямых линий. Проведя из каждой точки дугу, радиусом больш отрезка ab, найдём центр сопряжения — точку О. Из центра сопряжения проведём дугу заданного радиуса сопряжения R.
Видео:Сопряжение окружностейСкачать

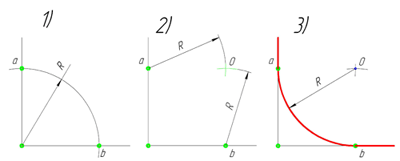
Сопряжение окружностей(дуг) с прямой линией
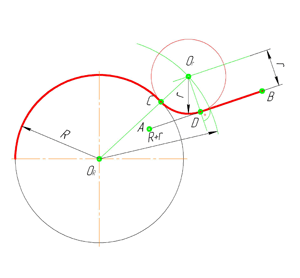
Внешнее сопряжение дуги и прямой линии
В этом примере будет построено сопряжение заданным радиусом r прямой линии, заданной отрезком AB, и дуги окружности радиусом R.
Сначала найдём центр сопряжения. Для этого проведём прямую, параллельную отрезку AB и отстоящую от него на расстояние радиуса сопряжения r, и дугу, из центра окружности O R радиусом R+r. Точка пересечения дуги и прямой и будет центром сопряжения – точкой О r .
Из центра сопряжения, точки О r , опустим перпендикуляр на прямую AB. Точка D, полученная на пересечении перпендикуляра и отрезка AB, и будет точкой сопряжения. Найдём вторую точку сопряжения на дуге окружности. Для этого соединим центр окружности О R и центр сопряжения О r линией. Получим вторую точку сопряжения – точку C. Из центра сопряжения проведём дугу сопряжения радиусом r, соединив точки сопряжения.
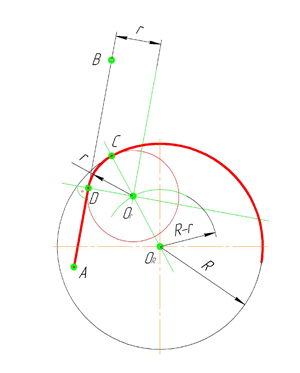
Внутреннее сопряжение прямой линии с дугой
По аналогии строится внутреннее сопряжение прямой линии с дугой. Рассмотрим пример построения сопряжения радиусом r прямой линии, заданной отрезком AB, и дуги окружности радиуса R. Найдём центр сопряжения. Для этого построим прямую, параллельную отрезку AB и отстоящую от него на расстояние радиуса r, и дугу, из центра окружности O R радиусом R-r. Точка О r , полученная на пересечении прямой и дуги, и будет центром сопряжения.
Из центра сопряжения(точка О r ) опустим перпендикуляр на прямую AB. Точка D, полученная на основании перпендикуляра, и будет точкой сопряжения.
Для нахождения второй точки сопряжения на дуге окружности, соединим центр сопряжения Оr и центр окружности О R прямой линией. На пересечении линии с дугой окружности получим вторую точку сопряжения – точку C. Из точки О r , центра сопряжения, проведём дугу радиусом r, соединив точки сопряжения.
Видео:Внешнее сопряжение окружностей. Черчение. Тема 9. Задача 6.Скачать

Сопряжение окружностей (дуг)
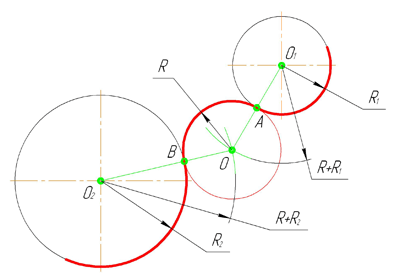
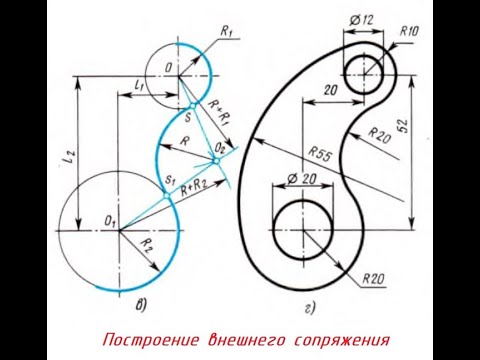
Внешнее сопряжение дуг окружностей
Внешним сопряжением считается сопряжение, при котором центры сопрягаемых окружностей(дуг) O1( радиус R1) и O2 (радиус R2) располагаются за сопрягающей дугой радиуса R. На примере рассмотрено внешнее сопряжение дуг. Сначала находим центр сопряжения. Центром сопряжения является точка пересечения дуг окружностей с радиусами R+R1 и R+R2, построенных из центров окружностей O1(R1) и O2(R2) соответственно. Затем центры окружностей O1 и O2 соединяем прямыми с центром сопряжения, точкой O, и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. После этого, из центра сопряжения строим дугу заданного радиуса сопряжения R и соединяем ей точки A и B.
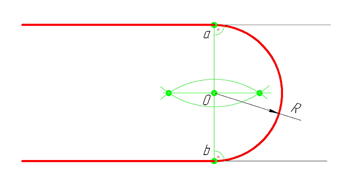
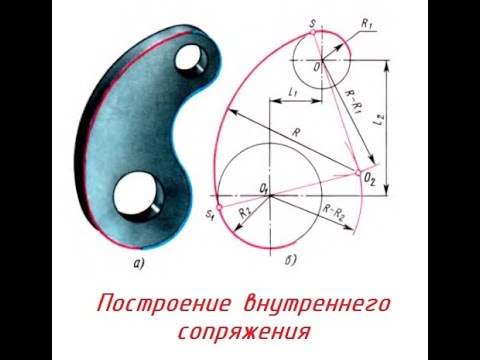
Внутреннее сопряжение дуг окружностей
Внутренним сопряжением называется сопряжение, при котором центры сопрягаемых дуг O1, радиуса R1, и O2, радиус R2, располагаются внутри сопрягающей их дуги заданного радиуса R. На картинке ниже приведён пример построения внутреннего сопряжения окружностей(дуг). Вначале мы находим центр сопряжения, которым является точка O, точка пересечения дуг окружностей с радиусами R-R1 и R-R2 проведённых из центров окружностей O1и O2 соответственно. После чего соединяем центры окружностей O1 и O2 прямыми линиями с центром сопряжения и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. Затем из центра сопряжения строим дугу сопряжения радиуса R и строим сопряжение.
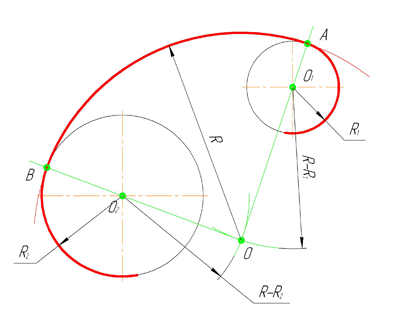
Смешанное сопряжение дуг окружностей
Смешанным сопряжением дуг является сопряжение, при котором центр одной из сопрягаемых дуг (O1) лежит за пределами сопрягающей их дуги радиуса R, а центр другой окружности(O2) – внутри её. На иллюстрации ниже приведён пример смешанного сопряжения окружностей. Сначала находим центр сопряжения, точку O. Для нахождения центра сопряжения строим дуги окружностей с радиусами R+R1, из центра окружности радиуса R1 точки O1, и R-R2, из центра окружности радиуса R2 точки O2. После чего соединяем центр сопряжения точку O с центрами окружностей O1 и O2 прямыми и на пересечении с линиями соответствующих окружностей получаем точки сопряжения A и B. Затем строим сопряжение.
Видео:Сопряжение окружностей #черчение #сопряжениеСкачать

Урок черчения в 7 классе «Построение сопряжений»
Видео:Построение ВНУТРЕННЕГО СОПРЯЖЕНИЯСкачать
«Управление общеобразовательной организацией:
новые тенденции и современные технологии»
Свидетельство и скидка на обучение каждому участнику
Описание презентации по отдельным слайдам:
Тема урока: «СОПРЯЖЕНИЯ» Геометрические построения – урок черчения в 7 классе
Цель: овладеть методикой построения сопряжений на чертежах, найти области применения графических знаний в практике. Задачи: познакомить учащихся с применением сопряжений в технических формах, предметах быта, окружающей среды; научить строить сопряжение между сторонами углов; развивать логическое мышление, познавательный интерес, умение работать чертежными инструментами; воспитывать точность, аккуратность, внимательность.
Актуализация опорных знаний 1. Какие линии называются параллельными? 2. Что такое перпендикуляр? 3. Какие геометрические фигуры вы знаете? 4. С помощью каких чертёжных инструментов можно построить перпендикуляр к прямой? 5. С помощью какого чертёжного инструмента можно провести окружность, дугу? 6. Назовите виды углов? 7. Как называются стороны угла?
Тему сегодняшнего урока вы узнаете, если отгадаете ребус СО+ПРЯЖ+ЕНИЕ ,, , , + + СОПРЯЖЕНИЕ
А знаете ли вы, что СОПРЯЖЕНИЯ встречаются в нашей жизни на каждом шагу? Посмотрите вокруг и вы увидите эти волшебные линии! Присмотримся внимательнее к архитектурным сооружениям, мебели и интерьерам квартир. Многие предметы включают в себя циркульные кривые, которые в черчении называют сопряжениями.
Старинная и современная архитектура
Так, форма поворота автотрассы – это дуга. Радиус поворота должен быть строго рассчитан с учётом скорости автомашин, едущих по дороге. Ведь если автомобилист не «впишется» в поворот, произойдёт катастрофа. Трассы автомобильные
Архитектура олимпийского СОЧИ 2014 Дворец зимнего спорта АЙСБЕРГ Конькобежный центр Адлер-арена Стадион ФИШТ Сочи
Линии, образующие поверхности сверхзвуковых самолетов, высокоскоростных поездов и автомобилей всегда плавные. Только обтекаемые корпуса дают им возможность развивать большую скорость (по законам аэродинамики).
Различная бытовая техника, оборудование, устройства также имеют элементы сопряжения. Рукояткам инструментов (отвёртка, рубанок, напильник, топор, и т. п.) также придают плавные формы, конструктор, прежде всего думает о том, чтобы они были удобны для руки. Во многих случаях сопряжения обусловлены техникой безопасности, эргономикой, технологией изготовления, расчётами на прочность.
Мебель офисная и жилая
А это наши находки! Мы гуляли по улицам нашего города и увидели много подобных линий!
Плавный переход одной линии в другую называется сопряжением. Для того, чтобы изготовить любую деталь или изделие, содержащие элементы сопряжения, необходимо овладеть алгоритмом построения сопряжений, используя чертёжные инструменты. Что же такое сопряжение?
Что нужно для построения сопряжения? 1. Знать радиус сопряжения (R) 2. Найти центр сопряжения (О) 3. Найти точки сопряжения (А, Б) АЛГОРИТМ ПОСТРОЕНИЯ 1. Пусть R=15мм, тогда от основных линий надо провести дополнительные параллельные линии на расстоянии 15мм. Пересекаясь, они образуют центр сопряжения – точку О. 2. Для того чтобы найти точки сопряжения, из найденного центра сопряжения к основным линиям проводим перпендикуляры. Пересечение перпендикуляра и основной линии образуют точку сопряжения – А, Б. 3. Из найденного центра сопряжения проводим дугу радиусом 15 мм, соединяя точки сопряжения. 4. И последний этап, обвести получившееся сопряжение сплошной толстой основной линией. Вначале обводят дугу, затем вертикальную и горизонтальную линии. Еще раз внимательно посмотрите на мониторе этапы построения сопряжения и вычертите их в тетради.
R R R О В А R=15
R R О В А R=15 R
Для закрепления материала выполним практическое задание по учебнику (рис.135): «Построить сопряжения углов в заданной фигуре радиусом 15мм».
Творческое домашнее задание 300 20 R15 200 100
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 936 человек из 80 регионов
Курс повышения квалификации
Современные методы арт-терапии: базовые техники
- Сейчас обучается 240 человек из 59 регионов
Курс повышения квалификации
Правополушарная живопись
- Сейчас обучается 401 человек из 70 регионов
Ищем педагогов в команду «Инфоурок»
- Литвинова Татьяна ВладимировнаНаписать 3057 07.06.2017
Номер материала: ДБ-538197
- 07.06.2017 261
- 07.06.2017 242
- 07.06.2017 954
- 07.06.2017 578
- 07.06.2017 236
- 07.06.2017 645
- 06.06.2017 984
Не нашли то, что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Федеральный перечень учебников будет дополнен новыми учебниками
Время чтения: 3 минуты
Первый мониторинг вузов РФ по новым показателям пройдёт в 2023 году
Время чтения: 2 минуты
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей
Время чтения: 1 минута
В Подмосковье вводят систему голосования оценки качества школьных столовых
Время чтения: 1 минута
В местах сдачи ЕГЭ будут применены антиковидные меры
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Видео:Сопряжение двух пересекающихся прямых. Урок 9. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Урок черчения в 7-м классе по теме «Сопряжения»
Разделы: Технология
Цели:
- познакомить учащихся с применением сопряжений в технических формах, предметах быта;
- научить строить сопряжение между сторонами углов;
- развивать логическое мышление, познавательный интерес, умение работать чертежными инструментами;
- воспитывать точность, аккуратность, внимательность.
Тип урока: комбинированный.
Методы проведения: фронтальный опрос, рассказ с демонстрацией, упражнения.
Материальное обеспечение: технические детали, мультимедиа.
Ход урока
I. Организационная часть (1 минута).
Проверка готовности к уроку, заполнение классного журнала.
II. Повторение пройденного материала по теме «Геометрические построения.
Деление окружностей на равные части». (5 минут).
Фронтальный опрос. Задание: разделить окружности на 3 и 5 равных частей.По окончании работы сдаются на проверку учителю.
III. Изучение нового материала.
1. Вступительная беседа. (3 минуты)
Тему сегодняшнего урока вы узнаете, если отгадаете ребус.1 слайд
Правильно, это сопряжение. Сопряжением называется плавный переход от одной линии к другой.
Сейчас мы с вами посмотрим технические детали и определим есть ли на них сопряжения. Действительно есть.
2 слайд. Посмотрите примеры применения сопряжений в технике.
Правильно: рукоятки инструментов, изгибы музыкальных инструментов, мебели, архитектурных сооружений. Вы поняли, что применение сопряжений очень разнообразно.
2. Объяснение построения сопряжения с помощью мультимедиа (10 минут). Сопряжения бывают разные
Теперь попробуем вместе с вами определить порядок построения сопряжения.
6 слайд. Вы уже поняли, что сопряжение это плавный переход, но ведь скругление может быть разным
Как вы думаете, что должно быть задано, чтобы мы начертили плавный переход нужного нам размера? Правильно, радиус. Значит, радиус должен быть задан.
Радиус задан, циркуль в руке и что? Мы не знаем куда поставить ножку циркуля с иголкой. Что нужно определить? Правильно, центр. Для этого от сторон угла мы откладываем размер, равный радиусу сопряжения и проводим линии построения параллельно сторонам угла до пересечения друг с другом. Точка пересечения и будет центром сопряжения.
Осталось провести дугу. Задумаемся, где начинается и заканчивается дуга? Значит, нам не хватает еще каких-то данных? Молодцы! Нам надо определить точки начала и конца дуги. Для этого мы опустим перпендикуляры из центра сопряжения на стороны угла. Таким образом мы определили точки сопряжения. Выполняем построение дуги, поставив ножку циркуля с иголкой в центр сопряжения, а ножку циркуля с карандашом в точку сопряжения. Чертеж сопряжения сторон угла закончен.
Мы с вами вместе составили алгоритм построения сопряжения. Запишите себе в тетрадь порядок построения сопряжения.
3. Закрепление изученного материала (24 минуты).
Выполнение упражнения (В учебнике рис. 135, стр. 105). Ученик работает у доски на заранее заготовленном чертеже детали
Во время выполнения чертежа даются необходимые пояснения.
4. Домашнее задание (2 минуты).
Страница учебника 106 , рисунок 137
Послесловие. Мои ученики выполняют по данной теме творческие работы. Я привожу примеры таких работ
Желаю всем успеха в нашей трудной, но интересной работе.
Используется учебник
Ботвинников А.Д. и др. Черчение: Учеб. для 7-8 кл. общеобразоват. Учреждений / А.Д. Ботвинников, В.Н. Виноградов, И.С. Вышнепольский. — М. Просвещение, 2005г.
🌟 Видео
Построение ВНЕШНЕГО СОПРЯЖЕНИЯСкачать
СОПРЯЖЕНИЕ ОКРУЖНОСТИ С ЛИНИЕЙ [pairing the circle with the line]Скачать
![СОПРЯЖЕНИЕ ОКРУЖНОСТИ С ЛИНИЕЙ [pairing the circle with the line]](https://i.ytimg.com/vi/oKj3m1n67wI/0.jpg)
Внешнее сопряжение двух дуг окружностей третьей дугой. Урок13.(Часть1.ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

НАЧЕРТИТЬ ЗАСОВ. ГЕОМЕТРИЧЕСКОЕ ЧЕРЧЕНИЕ. ИНЖЕНЕРНАЯ ГРАФИКА. ПЕРЕХОДЫ И СОПРЯЖЕНИЯСкачать

Внутреннее сопряжение двух дуг окружностей третьей дугой. Урок14.(Часть1.ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Сопряжение двух окружностейСкачать

СопряжениеСкачать

Построение СМЕШАННОГО СОПРЯЖЕНИЯСкачать

Внешнее сопряжение окружностей. Черчение. Тема 9. Задача 6.Скачать

Деление окружности на равные части. Урок 6. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Сопряжение двух окружностей.Скачать

ВСЯ СУТЬ СОПРЯЖЕНИЙ И ПЕРЕХОДОВ. Правило построения сопряжений. Геометрические построенияСкачать

Сопряжения. Часть 1.Скачать