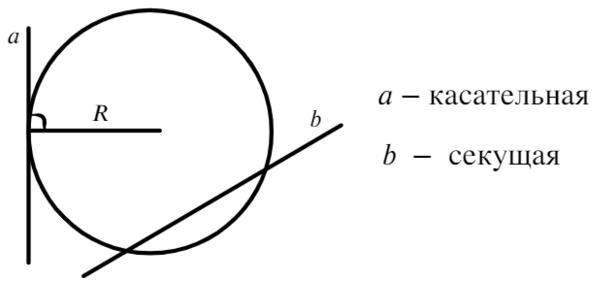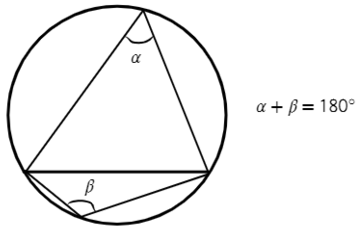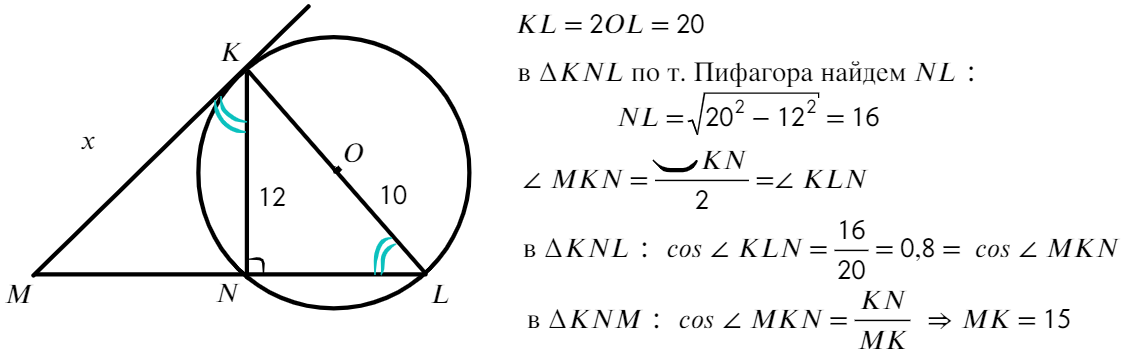- Длина окружности
- Задачи на длину окружности
- Задачи на площадь круга
- Нахождение радиуса круга: формула и примеры
- Формулы вычисления радиуса круга
- 1. Через длину окружности/периметр круга
- 2. Через площадь круга
- Примеры задач
- Теория и практика окружности
- Аналогично в каждом отрезке присутствует точка, вне окружности (О).
- Задача №1. Дано на рисунке:
- Достаточно вспомнить свойства центральных и вписанных углов.
- Ответ: 39°
- Задача №2. Дано на рисунке:
- Найти нужно меньшую дугу BD
- Ответ: 100°
- Найти меньшую дугу ВС
- Ответ: 114°
- Задача №4. Дано на рисунке:
- Найти отрезок МК
- Ответ: МК = 15.
- Задача №5. Дано на рисунке:
- Попробуй найти подобные треугольники
- Ответ: 6
- Задача №5. Дано на рисунке:
- Без свойства секущей и касательной здесь будет тяжело
- Ответ: 12√7.
- Я могу долго тебе показывать, как решать задачи, но без твоих усилий ничего не выйдет.
- О треугольниках О четырехуголниках
- 💥 Видео
Видео:Длина окружности. Практическая часть - решение задачи. 6 класс.Скачать

Длина окружности
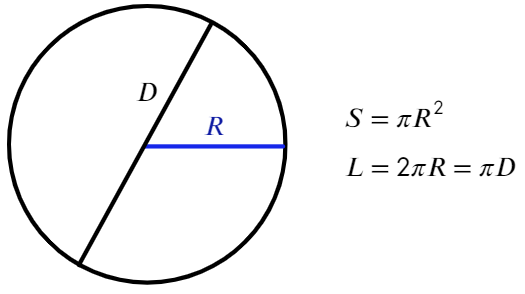
Длина любой окружности больше своего диаметра в одно и то же число раз, а именно, приблизительно в 3,14 раза. Для обозначения этой величины используется маленькая (строчная) греческая буква π (пи):
| C | = π. |
| D |
Таким образом, длину окружности (C) можно вычислить, умножив константу π на диаметр (D), или умножив π на удвоенный радиус, так как диаметр равен двум радиусам. Следовательно, формула длины окружности будет выглядеть так:
где C — длина окружности, π — константа, D — диаметр окружности, R — радиус окружности.
Так как окружность является границей круга, то длину окружности можно также назвать длиной круга или периметром круга.
Видео:Длина окружности. Площадь круга - математика 6 классСкачать

Задачи на длину окружности
Задача 1. Найти длину окружности, если её диаметр равен 5 см.
Решение: Так как длина окружности равна π умноженное на диаметр, то длина окружности с диаметром 5 см будет равна:
C ≈ 3,14 · 5 = 15,7 (см).
Задача 2. Найти длину окружности, радиус которой равен 3,5 м.
Решение: Сначала найдём диаметр окружности, умножив длину радиуса на 2:
теперь найдём длину окружности, умножив π на диаметр:
C ≈ 3,14 · 7 = 21,98 (м).
Задача 3. Найти радиус окружности, длина которой равна 7,85 м.
Решение: Чтобы найти радиус окружности по её длине, надо длину окружности разделить на 2π:
| R | = | C | , |
| 2π |
следовательно, радиус будет равен:
| R | ≈ | 7,85 | = | 7,85 | = 1,25 (м). |
| 2 · 3,14 | 6,28 |
Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Задачи на площадь круга
Задача 1. Найти площадь круга, если его радиус равен 2 см.
Решение: Так как площадь круга равна π умноженное на радиус в квадрате, то площадь круга с радиусом 2 см будет равна:
S ≈ 3,14 · 2 2 = 3,14 · 4 = 12,56 (см 2 ).
Ответ: 12,56 см 2 .
Задача 2. Найти площадь круга, если его диаметр равен 7 см.
Решение: Сначала найдём радиус круга, разделив его диаметр на 2:
теперь вычислим площадь круга по формуле:
S = πr 2 ≈ 3,14 · 3,5 2 = 3,14 · 12,25 = 38,465 (см 2 ).
Данную задачу можно решить и другим способом. Вместо того чтобы сначала находить радиус, можно воспользоваться формулой нахождения площади круга через диаметр:
| S = π | D 2 | ≈ 3,14 · | 7 2 | = 3,14 · | 49 | = |
| 4 | 4 | 4 |
| = | 153,86 | = 38,465 (см 2 ). |
| 4 |
Ответ: 38,465 см 2 .
Задача 3. Найти радиус круга, если его площадь равна 12,56 м 2 .
Решение: Чтобы найти радиус круга по его площади, надо площадь круга разделить π, а затем из полученного результата извлечь квадратный корень:
Видео:Окружность и круг, 6 классСкачать

Нахождение радиуса круга: формула и примеры
В данной публикации мы рассмотрим, как можно вычислить радиус круга (окружности) и разберем примеры решения задач для закрепления материала.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Формулы вычисления радиуса круга
1. Через длину окружности/периметр круга
Радиус круга/окружности рассчитывается по формуле:
C – это длина окружности/периметр круга; равняется удвоенному произведению числа π на его радиус:
C = 2 π R
π – число, приближенное значение которого равно 3,14.
2. Через площадь круга
Радиус круга/окружности вычисляется таким образом:
S – это площадь круга; равна числу π , умноженному на квадрат его радиуса:
S = π R 2
Видео:КАК НАЙТИ РАДИУС КРУГА (ОКРУЖНОСТИ), ЕСЛИ ИЗВЕСТНА ДЛИНА ОКРУЖНОСТИ? Примеры | МАТЕМАТИКА 6 классСкачать

Примеры задач
Задание 1
Длина окружности равняется 87,92 см. Найдите ее радиус.
Решение:
Используем первую формулу (через периметр):
Задание 2
Найдите радиус круга, если его площадь составляет 254,34 см 2 .
Решение:
Воспользуемся формулой, выраженной через площадь фигуры:
Видео:Математика 6 класс (Урок№76 - Длина окружности. Площадь круга.)Скачать

Теория и практика окружности
Свойства касательных и секущих.
Площадь, сектор, длина окружности.
Задачи на окружности.
По статистике окружности никто не любит, но при этом леденец любим, солнце любим, давай и окружность полюбим!
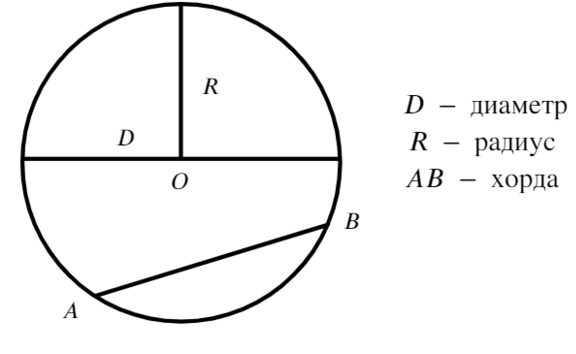
Окружность − геометрическое место точек плоскости, равноудаленных от одной ее точки (центра). На рисунке центр − точка О.
В окружности может быть проведено 3 типа отрезка:
Отрезок, проходящий через две точки окружности, но не через центр, называют хордой (AB).
Хорда, проходящая через центр окружности, называется диаметром (самая большая хорда в окружности − диаметр (D)).
Радиус − отрезок, соединяющий центр окружности с точкой на окружности. Диаметр в два раза больше радиуса (R).
А также две прямые снаружи от окружности:
Касательная имеет одну общую точку с окружностью. Сразу стоит сказать о том, что радиус, проведенный в точку касания, будет иметь с касательной угол 90°.
Секущая пересекает окружность в двух точках, внутри окружности получается хорда или, в частном случае, диаметр.
Теперь чуть-чуть об углах и дугах:
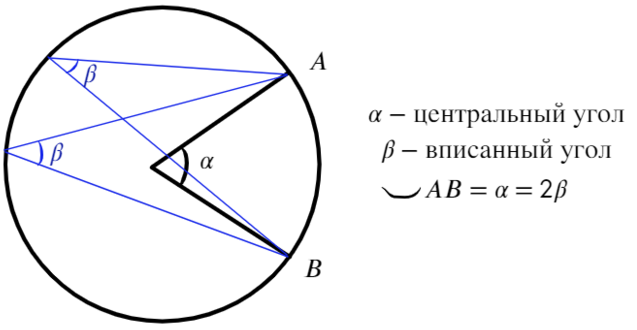
Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают ее. Он в два раза меньше дуги, на которую опирается.
Центральный угол — это угол, вершина которого находится в центре окружности, равен дуге на которую опирается.
Вписанные углы, опирающиеся на одну дугу, равны между собой (β=β=α/2) и равны половине дуги, на которую опираются.
Градусная мера дуги – величина в °, соответствует центральному углу. Длина дуги равна α.
А вот такой угол НЕвписанный, такой угол «никто и звать никак».
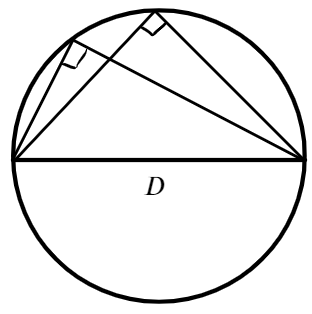
Можно сделать вывод, что вписанный угол, который опирается на половину дуги окружности, будет прямым, а также будет опираться на диаметр:
Любая пара углов, опирающихся на одну и ту же хорду, вершина которых находится по разные стороны от хорды, составляет в сумме 180°.
Запишем основные свойства углов в окружности:
Нашел что-то общее?
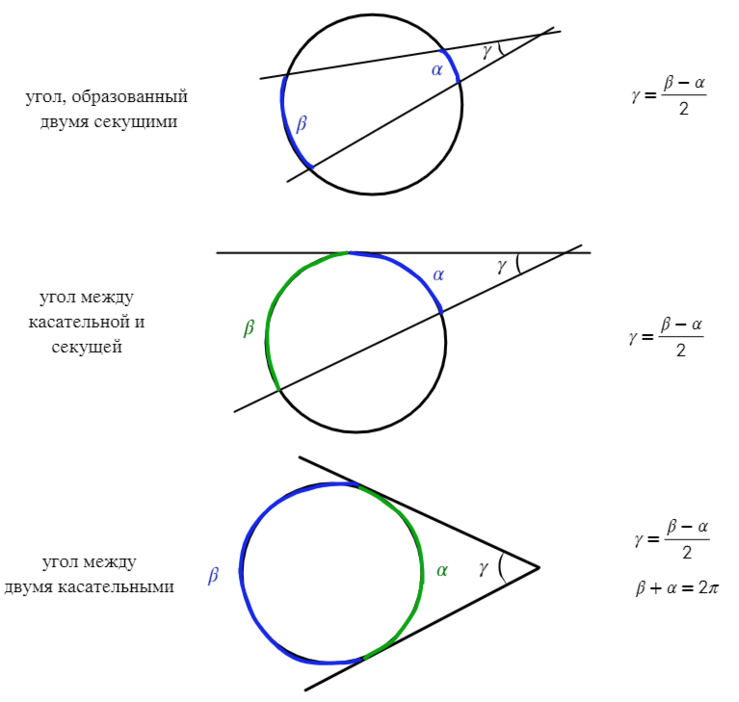
Если угол находится вне окружности, без разницы, чем он получен (касательной или секущей), то найти его можно через половину разности дуг.
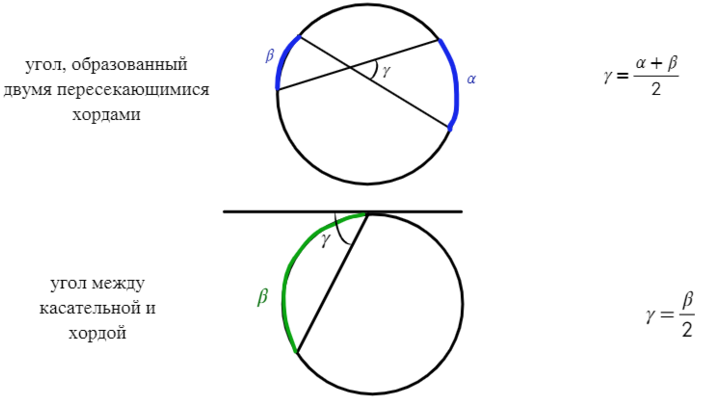
Если угол находится внутри окружности, то находим его через полусумму дуг.
Если есть одна дуга, которая находится на требуемом угле, то угол равен половине этой дуги.
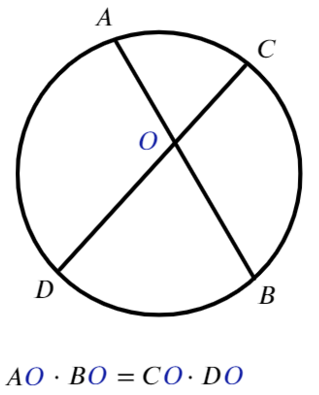
Для любых двух хорд, проходящих через некоторую точку О, выполняет равенство:
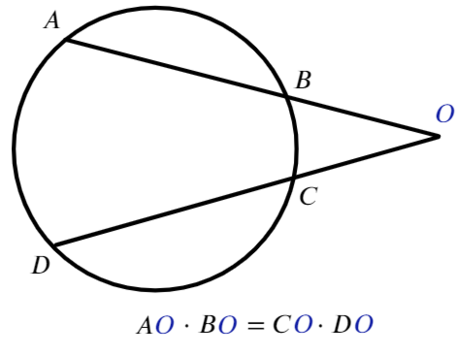
Для любых двух секущих, проходящих через некоторую точку O, выполняется равенство:
Согласен, что они похожи, особенно если не смотреть на картинки.
Как не перепутать такие равенства? В каждом отрезке должна присутствовать точка, вне окружности (О).
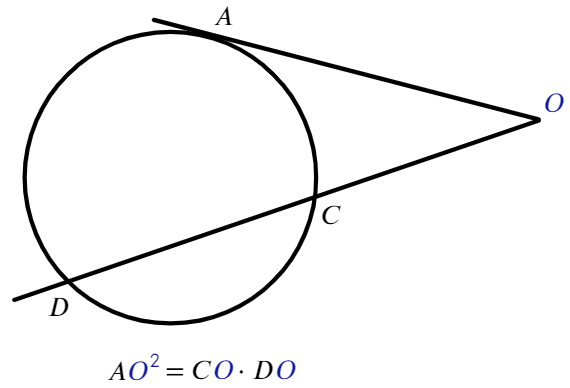
Если из точки, лежащей вне окружности, проведены касательная и секущая:
Аналогично в каждом отрезке присутствует точка, вне окружности (О).
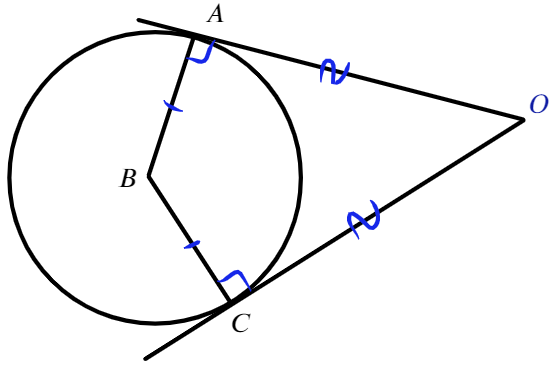
Если теперь провести две касательные из точки O, то получим такие равные отрезки:
Касательные равны, как, сообственно, и радиусы!
Площадь и длина окружности находятся по формуле:
По своему определению число π показывает, во сколько раз длина окружности больше диаметра, отсюда такая формула: L = πD
Если хочешь вывести площадь круга, можешь проинтегрировать длину окружности относительно R или вывести зависимость, как сделал Архимед!
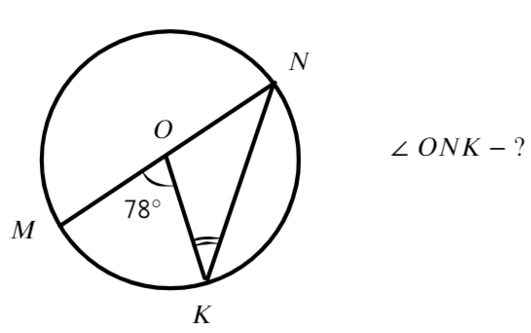
Задача №1. Дано на рисунке:
Достаточно вспомнить свойства центральных и вписанных углов.
Ответ: 39°
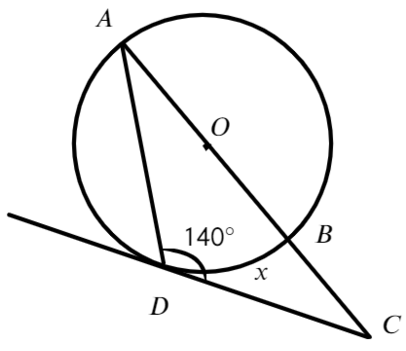
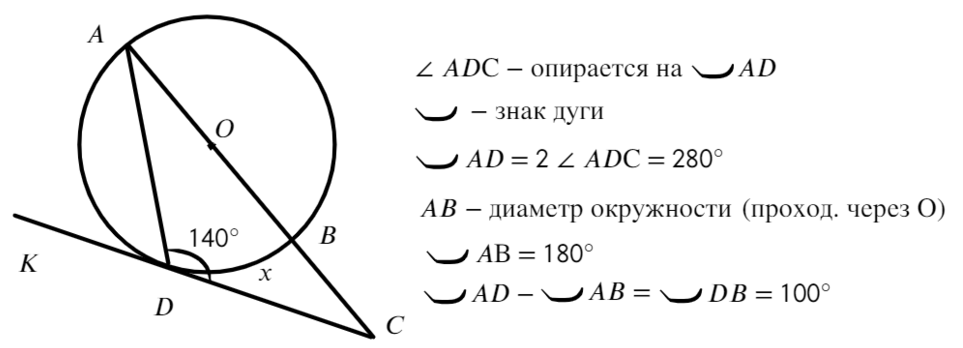
Задача №2. Дано на рисунке:
Найти нужно меньшую дугу BD
Ответ: 100°
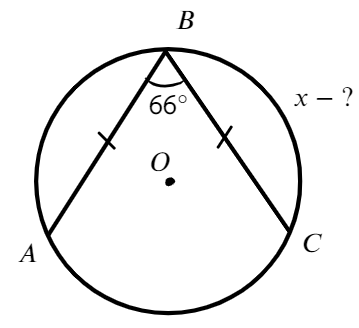
Задача №3. Дано на рисунке:
Найти меньшую дугу ВС
Ответ: 114°
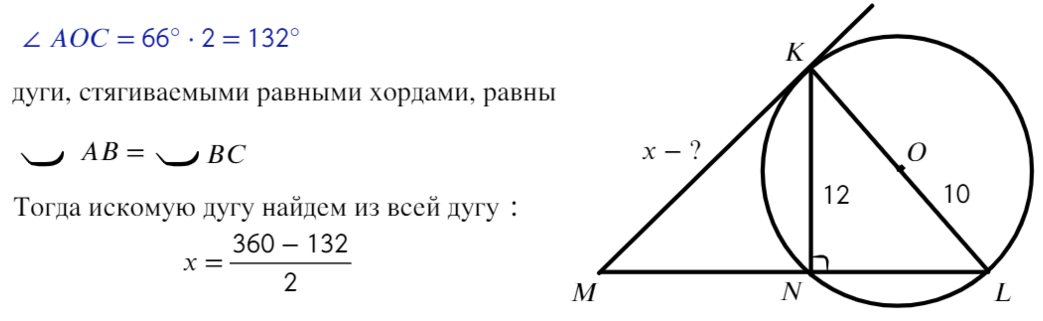
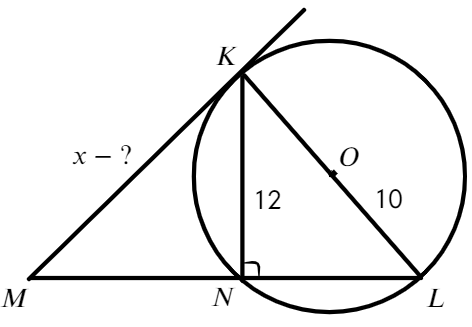
Задача №4. Дано на рисунке:
Найти отрезок МК
Ответ: МК = 15.
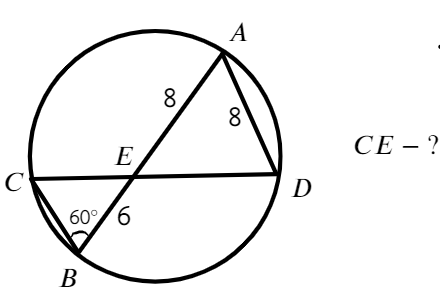
Задача №5. Дано на рисунке:
Попробуй найти подобные треугольники
Ответ: 6
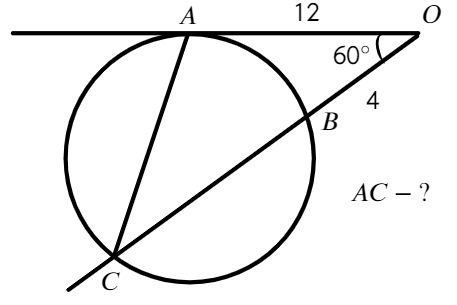
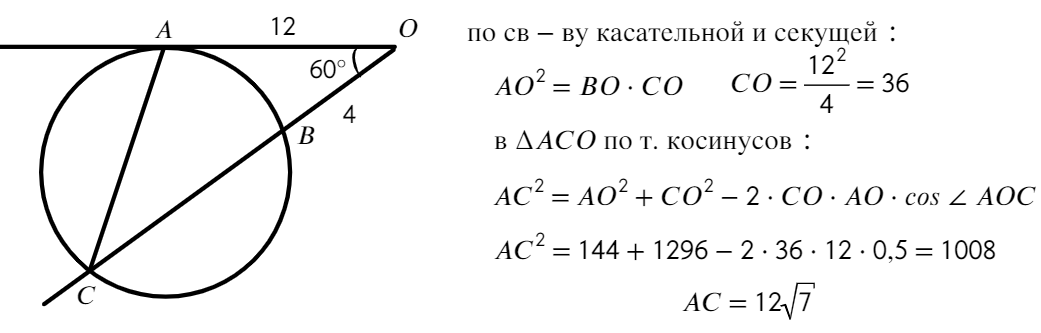
Задача №5. Дано на рисунке:
Без свойства секущей и касательной здесь будет тяжело
Ответ: 12√7.
Я могу долго тебе показывать, как решать задачи, но без твоих усилий ничего не выйдет.
О треугольниках
О четырехуголниках
p.s. Не бойся ошибаться и задавать вопросы!
Если нашел опечатку, или что-то непонятно − напиши.
💥 Видео
Длина окружности. Математика 6 класс.Скачать

Интенсив к РЭ Максвелла для 7-8 классов | Движение по окружностиСкачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

10 класс, 11 урок, Числовая окружностьСкачать

Радиус описанной окружностиСкачать

Длина окружности. Площадь круга, 6 классСкачать

Окружность. 7 класс.Скачать

КАК НАЙТИ ДЛИНУ ОКРУЖНОСТИ, ЕСЛИ ИЗВЕСТЕН ДИАМЕТР ИЛИ РАДИУС? Примеры | МАТЕМАТИКА 6 классСкачать

Площадь круга. Математика 6 класс.Скачать

КАК ИЗМЕРИТЬ ДЛИНУ ОКРУЖНОСТИ? · ФОРМУЛА + примеры · Длина окружности как найти? Математика 6 классСкачать

Радиус и диаметрСкачать

РЕШЕНИЕ ЗАДАЧИ НА НАХОЖДЕНИЕ РАДИУСА ОКРУЖНОСТИ. Задачи | МАТЕМАТИКА 6 классСкачать

Найти центр и радиус окружностиСкачать