Как найти разность нескольких векторов

В данной публикации мы рассмотрим, как найти сумму и разность векторов, приведем геометрическую интерпретацию, а также формулы, свойства и примеры этих действий.

Сумма векторов

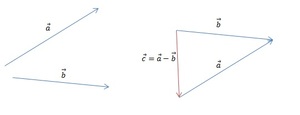
Сложение векторов выполняется по правилу треугольника.

Геометрическая интерпретация:

Суммой a и b является вектор c , начало которого совпадает с началом a , а конец – с концом b . При этом конец вектора a должен совпадать с началом вектора b .

Для сложения векторов также используется правило параллелограмма.

Два неколлинеарных вектора a и b можно привести к общему началу, и в этом случае их суммой является вектор c , совпадающий с диагональю параллелограмма и берущий начало в той же точке, что и исходные векторы.

Формула сложения векторов

Элементы вектора c равняются попарной сумме соответствующих элементов a и b .

<table data-id="250" data-view-id="250_55602" data-title="Формулы сложения векторов" data-currency-format="$1,000.00" data-percent-format="10.00%" data-date-format="DD.MM.YYYY" data-time-format="HH:mm" data-features="["after_table_loaded_script"]" data-search-value="" data-lightbox-img="" data-head-rows-count="1" data-pagination-length="50,100,All" data-auto-index="off" data-searching-settings="» data-lang=»default» data-override=»» data-merged=»[]» data-responsive-mode=»2″ data-from-history=»0″>

Для плоских задач

<td data-cell-id="B1" data-x="1" data-y="1" data-db-index="1" data-cell-type="text" data-original-value=" a + b = <a_x + b_x; a_y + b_y> » data-order=» a + b = <a_x + b_x; a_y + b_y> » style=»min-width:55.0847%; width:55.0847%;»> a + b = <a_x + b_x; a_y + b_y>Для трехмерных задач

<td data-cell-id="B2" data-x="1" data-y="2" data-db-index="2" data-cell-type="text" data-original-value=" a + b = <a_x + b_x; a_y + b_y; a_z + b_z> » data-order=» a + b = <a_x + b_x; a_y + b_y; a_z + b_z> «> a + b = <a_x + b_x; a_y + b_y; a_z + b_z>Для n-мерных векторов

<td data-cell-id="B3" data-x="1" data-y="3" data-db-index="3" data-cell-type="text" data-original-value=" a + b = <a₁ + b₁; a₂ + b₂; . a_n + b_n> » data-order=» a + b = <a₁ + b₁; a₂ + b₂; . a_n + b_n> «> a + b = <a₁ + b₁; a₂ + b₂; . a_n + b_n>

Свойства сложения векторов

1. Коммутативность: a + b = b + a

2. Ассоциативность: ( a + b ) + c = a + ( b + c )

3. Прибавление к нулю: a + 0 = a

4. Сумма противоположных векторов: a + (- a ) = 0

Примечание: Вектор – a коллинеарен и равен по длине a , но имеет противоположное направление, из-за чего называется противоположным.

Разность векторов

Для вычитания векторов также применяется правило треугольника.

Если из вектора a вычесть b , то получится c , причем должно соблюдаться условие:

Формула вычитания векторов

Элементы вектора c равны попарной разности соответствующих элементов a и b .

<table data-id="251" data-view-id="251_83403" data-title="Формулы вычитания векторов" data-currency-format="$1,000.00" data-percent-format="10.00%" data-date-format="DD.MM.YYYY" data-time-format="HH:mm" data-features="["after_table_loaded_script"]" data-search-value="" data-lightbox-img="" data-head-rows-count="1" data-pagination-length="50,100,All" data-auto-index="off" data-searching-settings="» data-lang=»default» data-override=»» data-merged=»[]» data-responsive-mode=»2″ data-from-history=»0″>

Для плоских задач

<td data-cell-id="B1" data-x="1" data-y="1" data-db-index="1" data-cell-type="text" data-original-value=" a — b = <a_x — b_x; a_y — b_y> » data-order=» a — b = <a_x — b_x; a_y — b_y> » style=»min-width:55.0847%; width:55.0847%;»> a — b = <a_x — b_x; a_y — b_y>Для трехмерных задач

<td data-cell-id="B2" data-x="1" data-y="2" data-db-index="2" data-cell-type="text" data-original-value=" a — b = <a_x — b_x; a_y — b_y; a_z — b_z> » data-order=» a — b = <a_x — b_x; a_y — b_y; a_z — b_z> «> a — b = <a_x — b_x; a_y — b_y; a_z — b_z>Для n-мерных векторов

<td data-cell-id="B3" data-x="1" data-y="3" data-db-index="3" data-cell-type="text" data-original-value=" a — b = <a₁ — b₁; a₂ — b₂; . a_n — b_n> » data-order=» a — b = <a₁ — b₁; a₂ — b₂; . a_n — b_n> «> a — b = <a₁ — b₁; a₂ — b₂; . a_n — b_n>

Примеры задач

Задание 1
Вычислим сумму векторов и .

Задание 2
Найдем разность векторов и .

Определение разности двух векторов

В математике и физике студентам и школьникам зачастую попадаются задачи на векторные величины и на выполнение различных операций над ними. В чём же отличие векторных величин от привычных нам скалярных, единственная характеристика которых — это численное значение? В том, что они обладают направлением.
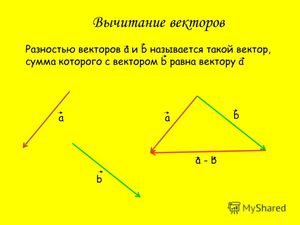
[block >

Определения векторной математики

Введём главные определения, используемые при выполнении линейных операций.

1. Вектором называют направленный (имеющий точку начала и точку конца) отрезок.
2. Длина (модуль) — это длина направленного отрезка.
3. Коллинеарными называют такие два вектора, которые либо параллельны одной и той же прямой, либо одновременно лежат на ней.
4. Противоположно направленными векторами называют коллинеарные и при этом направленные в разные стороны. Если же их направление совпадает, то они являются сонаправленными.
5. Вектора являются равными, когда они сонаправлены и одинаковы по модулю.
6. Суммой двух векторов a и b является такой вектор c, начало которого совпадает с началом первого, а конец — с концом второго при условии, что b начинается в той же точке, в которой заканчивается a.
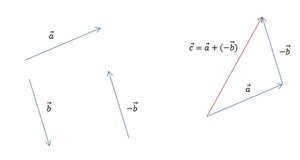
7. Разностью векторов a и b называют сумму a и (—b), где (—b) — противоположно направленный к вектору b. Также определение разности двух векторов может быть дано следующее: разностью c пары векторов a и b называют такой c, который при сложении с вычитаемым b образует уменьшаемое a.

Аналитический метод

Аналитический способ подразумевает получение координат разности по формуле без построения. Возможно выполнить вычисление для плоского (двухмерного), объёмного (трёхмерного) или же n-мерного пространства.

Для двухмерного пространства и векторных величин a <a₁; a₂> и b <b₁; b₂> расчёты будут иметь следующий вид: c <c₁; c₂> = <a₁ — b₁; a₂ — b₂>.

В случае с добавлением третьей координаты расчёт будет проводиться аналогично, и для a <a₁; a₂; a₃> и b <b₁; b₂; b₃> координаты разности будут также получены попарным вычитанием: c <c₁; c₂; c₃> = <a₁ — b₁; a₂ — b₂; a₃ — b₃>.

Вычисление разности графически

Для того чтобы построить разность графическим способом, следует воспользоваться правилом треугольника. Для этого необходимо выполнить следующую последовательность действий:

1. По заданным координатам построить векторы, для которых нужно найти разность.
2. Совместить их концы (т. е. построить два направленных отрезка, равных заданным, которые будут оканчиваться в одной и той же точке).
3. Соединить начала обоих направленных отрезков и указать направление; результирующий будет начинаться в той же точке, где начинался вектор, являющийся уменьшаемым, и заканчиваться в точке начала вычитаемого.

[block > Результат операции вычитания показан на рисунке ниже.

Также существует метод построения разности, незначительно отличающийся от предыдущего. Его суть заключается в применении теоремы о разности векторов, которая формулируется следующим образом: для того чтобы найти разность пары направленных отрезков, достаточно найти сумму первого из них с отрезком, противоположно направленным ко второму. Алгоритм построения будет иметь следующий вид:

1. Построить исходные направленные отрезки.
2. Тот, что является вычитаемым, необходимо отразить, т. е. построить противоположно направленный и равный ему отрезок; затем совместить его начало с уменьшаемым.
3. Построить сумму: соединить начало первого отрезка с концом второго.

Результат такого решения изображён на рисунке:

Решение задач

Для закрепления навыка разберём несколько заданий, в которых требуется рассчитать разность аналитически или графически.

Задача 1. На плоскости заданы 4 точки: A (1; —3), B (0; 4), C (5; 8), D (—3; 2). Определить координаты вектора q = AB — CD, а также рассчитать его длину.

Решение. Вначале следует найти координаты AB и CD. Для этого из координат конечных точек вычтем координаты начальных. Для AB началом является A (1; —3), а концом — B (0; 4). Рассчитаем координаты направленного отрезка:

Аналогичный расчёт выполняется для CD:

Теперь, зная координаты, можно найти разность векторов. Формула для аналитического решения плоских задач была рассмотрена ранее: для c = a — b координаты имеют вид <c₁; c₂> = <a₁ — b₁; a₂ — b₂>. Для конкретного случая можно записать:

Чтобы найти длину q, воспользуемся формулой | q | = √(q₁² + q₂²) = √((— 9)² + (— 1)²) = √(81 + 1) = √82 ≈ 9,06.
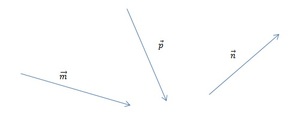
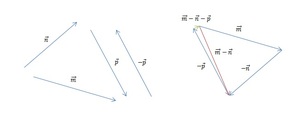
[block > Задача 2. На рисунке изображены векторы m, n и p.

Необходимо построить для них разности: p — n; m — n; m — n — p. Выяснить, какая из них обладает наименьшим модулем.

Решение. В задаче требуется выполнить три построения. Рассмотрим каждую часть задания более подробно.

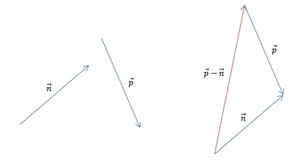
Часть 1. Для того чтобы изобразить p — n, воспользуемся правилом треугольника. Для этого при помощи параллельного переноса соединим отрезки так, чтобы совпала их конечная точка. Теперь соединим начальные точки и определим направление. В нашем случае вектор разности начинается там же, где и вычитаемый n.

Часть 2. Изобразим m — n. Теперь для решения воспользуемся теоремой о разности векторов. Для этого следует построить вектор, противоположный n, а затем найти его сумму с m. Полученный результат будет выглядеть так:

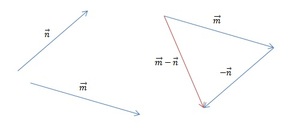
[block > Часть 3. Для того чтобы найти разность m — n — p, следует разбить выражение на два действия. Поскольку в векторной алгебре действуют законы аналогичные законам арифметики, то возможны варианты:

• m — (n + p): в этом случае вначале строится сумма n + p, которая затем вычитается из m;
• (m — n) — p: здесь сначала нужно найти m — n, а затем отнять от этой разности p;
• (m — p) — n: первым действием определяется m — p, после чего из полученного результата нужно вычесть n.

Так как в предыдущей части задачи мы уже нашли разность m — n, нам остаётся лишь вычесть из неё p. Построим разность двух данных векторов при помощи теоремы о разности. Ответ показан на изображении ниже (красным цветом обозначен промежуточный результат, а зелёным — окончательный).

Остаётся определить, модуль какого из отрезков является наименьшим. Вспомним, что понятия длины и модуля в векторной математике являются идентичными. Оценим визуально длины p — n, m — n и m — n — p. Очевидно, что самым коротким и обладающим наименьшим модулем является ответ в последней части задачи, а именно m — n — p.
[block > [block >

Вычитание векторов. Как найти разность векторов

Вы будете перенаправлены на Автор24

Откладывание вектора от данной точки

Для того, чтобы ввести разность векторов, сначала необходимо разобраться в таком понятии, как откладывание вектора от данной точки.

Введем следующую теорему:

От любой точки $K$ можно отложить вектор $overrightarrow$ и притом только один.

Доказательство.

Существование: Здесь нужно рассмотреть два случая:

В этом случае, очевидно, что искомый вектор — вектор $overrightarrow$.

Рисунок 2. Иллюстрация теоремы 1

Единственность: единственность сразу следует из построения, проведенного в пункте «существование».

Теорема доказана.

Вычитание векторов. Правило первое

Пусть нам даны векторы $overrightarrow$ и $overrightarrow$.

Готовые работы на аналогичную тему

Построение разности двух векторов рассмотрим с помощью задачи.

Решение.

Рисунок 3. Разность двух векторов

По правилу треугольника для построения суммы двух векторов видим, что

Из определения 2, получаем, что

Вычитание векторов. Правило второе

Вспомним следующее необходимое нам понятие.

Вектор $overrightarrow$ называется произвольным для вектора $overrightarrow$, если эти векторы противоположно направлены и имеют равную длину.

Для того чтобы ввести второе правило для разности двух векторов, нам необходимо в начале ввести и доказать следующую теорему.

Доказательство.

По определению 2, имеем

Прибавим к обеим частям вектор $left(-overrightarrowright)$, получим

Так как векторы $overrightarrow$ и $left(-overrightarrowright)$ противоположны, то $overrightarrow+left(-overrightarrowright)=overrightarrow$. Имеем

Теорема доказана.

Пример задачи на понятие разности векторов

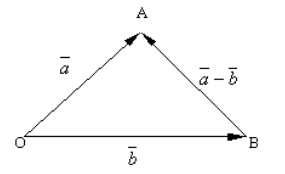
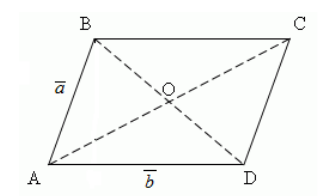
Рисунок 4. Параллелограмм

Решение.

а) Произведем сложение по правилу треугольника, получим

Из первого правила разности двух векторов, получаем

б) Так как $overrightarrow=overrightarrow$, получим

По теореме 2, имеем

Используя правило треугольника, окончательно имеем

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 01 04 2022

🌟 Видео