При исследовании поведения систем частиц, часто удобно использовать для описания движения такую точку, которая характеризует положение и движение рассматриваемой системы как единого целого. Такой точкой служит центр масс.
Для однородных тел обладающих симметрией центр масс часто совпадает с геометрическим центром тела. В однородном изотропном теле одной выделенной точке найдется симметричная ей точка.
- Радиус-вектор и координаты центра масс
- Скорость центра масс
- Примеры задач на определение центра масс
- 3.5. Центр масс
- Вектор скорости центра масс
- Вектор скорости центра масс
- Определение центра масс
- Радиус-вектор и координаты центра масс
- Скорость центра масс
- Примеры задач на определение центра масс
- Физический факультатив. Тема: «Импульс, центр масс, движение центра масс»
- 💥 Видео
Видео:Радиус векторСкачать

Радиус-вектор и координаты центра масс
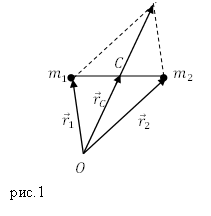
Предположим, что у нас имеются две частицы с равными массами, им соответствуют радиус-векторы: $<overline>_1 и <overline>_2$ . В этом случае центр масс расположен посередине между частицами. Центр масс (точка C) определён радиус-вектором $<overline>_C$ (рис.1).
Из рис.1 видно, что:
Можно ожидать, что вместе с геометрическим центром системы радиус-вектор, которого равен $<overline>_C,$ играет роль точка, положение которой определяет распределение массы. Ее определяют так, чтобы вклад каждой частицы был пропорционален ее массе:
Радиус -вектор $<overline>_C$, определенный выражением (2) — средне взвешенная величина радиус-векторов частиц $<overline>_1$ и $<overline>_2$. Это становится очевидным, если формулу (2) представить в виде:
Выражение (3) показывает, что радиус-вектор каждой частицы входит в $<overline>_C$ с весом, который пропорционален его массе.
Выражение (3) легко обобщается для множества материальных точек, которые расположены произвольным образом.
Если положения N материальных точек системы задано при помощи их радиус-векторов, то радиус — вектор, определяющий положение центра масс находим как:
Выражение (4) считают определением центра масс системы.
При этом абсцисса центра масс равна:
Ордината ($y_c$) центра масс и его аппликата ($z_c$):
Формулы (4-7) совпадают с формулами, которые используют для определения тяжести тела. В том случае, если размеры тела малы в сравнении с расстоянием до центра Земли, центр тяжести считают совпадающим с центром масс тела. В большинстве задач центр тяжести совпадает с центром масс тела.
Видео:3.3. Центр масс и закон его движения | Динамика | Александр Чирцов | ЛекториумСкачать

Скорость центра масс
Выражение для скорости центра масс ($<overline>_c=frac<d<overline>_c>
где $overline
$ — суммарный импульс системы частиц; $M$ масса системы. Выражение (8) справедливо при движениях со скоростями которые существенно меньше скорости света.
Если система частиц является замкнутой, то сумма импульсов ее частей не изменяется. Следовательно, скорость центра масс при этом величина постоянная. Говорят, что центр масс замкнутой системы перемещается по инерции, то есть прямолинейно и равномерно, и это движение не зависимо от движения составных частей системы. В замкнутой системе могут действовать внутренние силы, в результате их действия части системы могут иметь ускорения. Но это не оказывает влияния на движение центра масс. Под действием внутренних сил скорость центра масс не изменяется.
Видео:Урок 79. Центр масс тела и методы определения его положенияСкачать

Примеры задач на определение центра масс
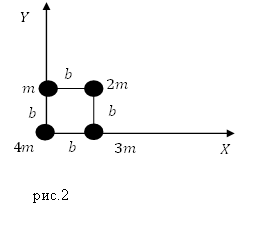
Задание. Система составлена из материальных точек (рис.2), запишите координаты ее центра масс?
Решение. Рассмотрим рис.2. Центр масс системы лежит на плоскости, значит, у него две координаты ($x_c,y_c$). Найдем их используя формулы:
Вычислим массу рассматриваемой системы точек:
Тогда абсцисса центра масс $x_ $равна:
Ответ. $x_c=0,5 b$; $y_с=0,3 b$
Задание. Космонавт, имеющий массу $m$, неподвижен относительно корабля массы $M$. Двигатель космического аппарата выключен. Человек начинает подтягиваться к кораблю при помощи легкого троса. Какое расстояние пройдет космонавт ($s_1$), какое корабль ($s_2$) до точки встречи? В начальный момент расстояние между ними равно $s$.
Решение. Центр масс корабля и космонавта лежит на прямой, соединяющей эти объекты.
В космосе, где внешние силы отсутствуют, центр масс замкнутой системы (корабль-космонавт) либо покоится, либо движется с постоянной скоростью. В избранной нами (инерциальной) системе отсчета он покоится. При этом:
Видео:2.4. Радиус-вектор и вектор перемещенияСкачать

3.5. Центр масс
Снова рассмотрим ту же систему материальных точек. Построим радиус-вектор 
где 


Радиус-вектор 
Вовсе не обязательно, что в центре масс системы окажется какая-то материальная точка.
Пример. Найдем центр масс системы, состоящей из двух маленьких шариков — материальных точек, соединенных невесомым стержнем (рис. 3.29). Такая система тел называется гантелей.
Рис. 3.29. Центр масс гантели
Из рис. видно, что
Подставляя в эти равенства выражение для радиус-вектора центра масс
Отсюда следует, что центр масс лежит на прямой, проходящей через центры шаров. Расстояния l1 и l2 между шарами и центром масс равны соответственно
Центр масс ближе к тому шарику, масса которого больше, что видно из отношения:
Определим, с какой скоростью движется центр инерции системы. Дифференцируем по времени обе части:
В числителе полученного выражения в правой части стоит сумма импульсов всех точек, то есть импульс 
Мы получили, что скорость центра инерции связана с импульсом системы и ее полной массой таким же соотношением, какое справедливо для материальной точки:
Видео 3.11. Движение центра масс двух одинаковых тележек, связанных пружиной.
Таким образом, можно считать, что скорость VC является скоростью системы как целого. Она, разумеется, может отличаться от скоростей каждого из тел, входящих в систему.
Центр масс замкнутой системы движется всегда с постоянной скоростью, поскольку импульс такой системы сохраняется.
Если продифференцировать теперь выражение для импульса системы по времени и учесть, что производная импульса системы есть равнодействующая внешних сил, то получим уравнение движения центра масс системы в общем случае:
Центр масс системы движется точно так же, как двигалась бы материальная точка с массой, равной массе всех частиц системы, под действием векторной суммы всех внешних сил, приложенных к системе.
Если имеется система материальных точек, внутреннее расположение и движение которых нас не интересует, мы вправе считать ее материальной точкой с координатами радиус-вектора центра инерции и массой, равной сумме масс материальных точек системы.
Если связать с центром масс замкнутой системы материальных точек (частиц) систему отсчета (ее называют системой центра масс), то полный импульс всех частиц в такой системе окажется равным нулю. Таким образом, в системе центра масс замкнутая система частиц как целое покоится, и существует только движение частиц относительно центра масс. Поэтому ясно выявляются свойства внутренних процессов, протекающих в замкнутой системе.
В случае, когда системой является тело с непрерывным распределением масс, определение центра масс остается по существу тем же. Окружаем произвольную точку 




Если вещество тела однородно, плотность его постоянна, и ее можно вынести из-под знака интеграла, так что она сократится в числителе и знаменателе. Тогда выражение для радиус-вектора центра масс тела принимает вид
где 
И в случае непрерывного распределения масс справедливо утверждение, что
Центр масс твердого тела движется так, как двигалась бы материальная точка с массой, равной массе тела, под действием векторной суммы всех внешних сил,приложенных к телу.
Пример. Если снаряд взрывается в некоторой точке своей параболической траектории, то осколки летят по самым различным траекториям, но его центр масс продолжает движение по параболе.
Видео:Найти центр и радиус окружностиСкачать

Вектор скорости центра масс
Видео:Радиус-векторыСкачать

Вектор скорости центра масс
Понятие центра масс .
В ряде случаев для упрощения решения задачи описания движения в системах, состоящих из большого количества частиц, полезно использовать понятие центра масс. Как мы увидим в дальнейшем понятие центра масс позволяет так же охарактеризовать движение системы как целого.
Центром масс системы называется точка, радиус-вектор которой rc задается уравнением:
где mi и ri — масса и радиус-вектор i-й частицы системы;
M — масса системы.
Другими словами, центр масс представляет собой среднее взвешенное значение радиус-векторов отдельных частиц с весовыми множителями, равными отношению соответствующих масс частиц к массе системы.
Скорость центра масс .
Скорость центра масс Vc можно найти как производную от радиус-вектора центра масс по времени, т.е. путем дифференцирования выражения (9) по времени. Следовательно ,
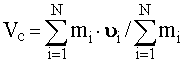
Числитель выражения (10) представляет собой импульс системы. Он равен произведению массы системы на скорость центра масс :
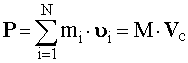
Видео:Определение центра масс #shorts #физика #егэСкачать

Определение центра масс
При исследовании поведения систем частиц, часто удобно использовать для описания движения такую точку, которая характеризует положение и движение рассматриваемой системы как единого целого. Такой точкой служит центр масс.
Для однородных тел обладающих симметрией центр масс часто совпадает с геометрическим центром тела. В однородном изотропном теле одной выделенной точке найдется симметричная ей точка.
Видео:Как найти центр и радиус нарисованной окружности #математика #егэ2023 #школа #fyp #shortsСкачать

Радиус-вектор и координаты центра масс
Предположим, что у нас имеются две частицы с равными массами, им соответствуют радиус-векторы: $ >_1 и >_2$ . В этом случае центр масс расположен посередине между частицами. Центр масс (точка C) определён радиус-вектором $ >_C$ (рис.1).
Из рис.1 видно, что:
Можно ожидать, что вместе с геометрическим центром системы радиус-вектор, которого равен $ >_C,$ играет роль точка, положение которой определяет распределение массы. Ее определяют так, чтобы вклад каждой частицы был пропорционален ее массе:
Радиус -вектор $ >_C$, определенный выражением (2) — средне взвешенная величина радиус-векторов частиц $ >_1$ и $ >_2$. Это становится очевидным, если формулу (2) представить в виде:
Выражение (3) показывает, что радиус-вектор каждой частицы входит в $ >_C$ с весом, который пропорционален его массе.
Выражение (3) легко обобщается для множества материальных точек, которые расположены произвольным образом.
Если положения N материальных точек системы задано при помощи их радиус-векторов, то радиус — вектор, определяющий положение центра масс находим как:
Выражение (4) считают определением центра масс системы.
При этом абсцисса центра масс равна:
Ордината ($y_c$) центра масс и его аппликата ($z_c$):
Формулы (4-7) совпадают с формулами, которые используют для определения тяжести тела. В том случае, если размеры тела малы в сравнении с расстоянием до центра Земли, центр тяжести считают совпадающим с центром масс тела. В большинстве задач центр тяжести совпадает с центром масс тела.
Видео:Урок 84. Теорема о движении центра массСкачать

Скорость центра масс
Выражение для скорости центра масс ($ >_c=frac >_c>
$ — суммарный импульс системы частиц; $M$ масса системы. Выражение (8) справедливо при движениях со скоростями которые существенно меньше скорости света.
Если система частиц является замкнутой, то сумма импульсов ее частей не изменяется. Следовательно, скорость центра масс при этом величина постоянная. Говорят, что центр масс замкнутой системы перемещается по инерции, то есть прямолинейно и равномерно, и это движение не зависимо от движения составных частей системы. В замкнутой системе могут действовать внутренние силы, в результате их действия части системы могут иметь ускорения. Но это не оказывает влияния на движение центра масс. Под действием внутренних сил скорость центра масс не изменяется.
Видео:Система материальных точек. Центр масс. Закон движения центра масс. Видеоурок по физике 10 классСкачать

Примеры задач на определение центра масс
Задание. Система составлена из материальных точек (рис.2), запишите координаты ее центра масс?
Решение. Рассмотрим рис.2. Центр масс системы лежит на плоскости, значит, у него две координаты ($x_c,y_c$). Найдем их используя формулы:
Вычислим массу рассматриваемой системы точек:
Тогда абсцисса центра масс $x_ $равна:
Ответ. $x_c=0,5 b$; $y_с=0,3 b$
Задание. Космонавт, имеющий массу $m$, неподвижен относительно корабля массы $M$. Двигатель космического аппарата выключен. Человек начинает подтягиваться к кораблю при помощи легкого троса. Какое расстояние пройдет космонавт ($s_1$), какое корабль ($s_2$) до точки встречи? В начальный момент расстояние между ними равно $s$.
Решение. Центр масс корабля и космонавта лежит на прямой, соединяющей эти объекты.
В космосе, где внешние силы отсутствуют, центр масс замкнутой системы (корабль-космонавт) либо покоится, либо движется с постоянной скоростью. В избранной нами (инерциальной) системе отсчета он покоится. При этом:
Видео:Движение центра масс твердого телаСкачать

Физический факультатив. Тема: «Импульс, центр масс, движение центра масс»
В работе рассмотрены некоторые задачи на движение центра масс, рассматриваемые на школьном факультативе по физике в Лицее научно-инженерного профиля города Королева. Представляется, что данная статья может быть полезной как для учителей физики школ с углубленным изучением предмета, так и для абитуриентов.
Импульс или количество движения материальной точки есть вектор, равный произведению массы этой точки m на вектор ее скорости v: 
Импульс силы – это вектор, равный произведению силы на время ее действия: 
Теорема об изменении импульса материальной точки. Пусть на материальную точку m действует постоянная сила F. Тогда


Импульс системы материальных точек равен по определению сумме импульсов всех N точек системы:
Изменение импульса системы материальных точек равно импульсу равнодействующей внешних сил, действующих на систему.
Изолированная (замкнутая) система – это такая система материальных точек, на которую не действуют внешние силы или их равнодействующая равна нулю.
Закон сохранения импульса: импульс изолированной системы материальных точек сохраняется, каково бы ни было взаимодействие между ними:
Если внешние силы, действующие на систему не равны нулю, но существует такое неизменное направление (например, ось OX), что сумма проекций внешних сил на это направление равна нулю, то проекция импульса системы на это направление сохраняется.
Центр масс системы материальных точек. Центром масс N материальных точек m1, m2,…, mN, положения которых заданы радиус-векторами 

Тогда координаты центра масс равны:



Скоростью центра масс является вектор

где 
Ускорением центра масс является вектор
где 
Теорема об ускорении центра масс системы материальных точек. Произведение суммы масс точек системы на ускорение центра масс равно сумме внешних сил, действующих на точки системы.
Если на систему материальных точек не действуют внешние силы, то скорость центра масс относительно любой инерциальной системы отсчета сохраняется, каково бы ни было взаимодействие внутри системы.
Если при этом скорость центра масс относительно некоторой инерциальной системы была равна нулю, то сохраняется и положение центра масс.
Два этих утверждения являются прямыми следствиями закона сохранения импульса.
Задача 1. Частица массы m движется со скоростью v, а частица массы 2m движется со скоростью 2v в направлении, перпендикулярном направлению движения первой частицы. На каждую частицу начинают действовать одинаковые силы. После прекращения действия сил первая частица движется со скоростью 2v направлении, обратном первоначальному. Определите скорость второй частицы. [1]
Изменение импульса частицы массой m вследствие действия импульса силы равно 3mv, следовательно вторая частица приобретает точно такой же импульс перпендикулярно направлению ее движения. Полный импульс второй частицы находится векторным сложением его составляющих по двум перпендикулярным направлениям и равен 5mv. Скорость второй частицы тогда равна 5v/2.
Задача 2. Ящик с песком массы М лежит на горизонтальной плоскости, коэффициент трения с которой равен µ. Под углом ? к вертикали в ящик со скоростью v влетает пуля массы m и почти мгновенно застревает в песке. Через какое время после попадания пули в ящик, начав двигаться, остановится? При каком значении ? он вообще не сдвинется? [1]
Решение. Изменение импульса системы материальных точек равно импульсу равнодействующей внешних сил, действующих на систему. По горизонтальной и вертикальной оси:
где u – скорость ящика сразу после того, как пуля в нем застрянет, N – реакция опоры, 
Так как пуля застревает почти мгновенно последним членом в правой части можно пренебречь. После того, как пуля застрянет, ящик тормозит под действие силы трения с ускорением 


Задача 3. По наклонной плоскости, составляющей угол а с горизонтом, с постоянной скоростью v съезжает ящик с песком массой M. В него попадает летящая горизонтально пуля массой m, и ящик при этом останавливается. С какой скоростью u летела пуля?
Решение. Вдоль наклонной плоскости изменение импульса системы
Поперек наклонной плоскости
Тогда
и с учетом того, что 
Задача 4. Обезьяна массы m уравновешена противовесом на блоке А. Блок А уравновешен грузом массы 2m на блоке В. Система неподвижна. Как будет двигаться груз, если обезьяна начнет равномерно выбирать веревку со скоростью u относительно себя? Массой блоков и трением пренебречь. [1]
Решение. Обезьяна получает импульс силы 


Задача 5. Из однородной круглой пластины радиусом R вырезали круг вдвое меньшего радиуса, касающийся края пластины. 
Решение. Пусть масса пластины до вырезания равна M. Тогда масса вырезанной части равна M/4. Предположим, что имеется в наличии вещество с отрицательной массой, Тогда вырез можно получить наложением на пластину пластинки с отрицательной массой —M/4. Тогда, поместив начало координат в центр круга и направив ось X направо, положение центра масс получаем из формулы для координаты центра масс:

Задача 6. На гладком полу стоит сосуд, заполненный водой плотности p0; объем воды V0. Оказавшийся на дне сосуда жук объема V и плотности p через некоторое время начинает ползти по дну сосуда со скоростью u относительно него. С какой скоростью станет двигаться сосуд по полу? 
Решение. Пусть скорость сосуда v, тогда скорость жука относительно пола u+v. Импульс системы по горизонтальной оси сохраняется и равен нулю. Удобно рассматривать жука как совокупность воды массой 


Задача 7. На дне маленькой запаянной пробирки, подвешенной над столом на нити, сидит муха, масса которой равна массе пробирки, а расстояние от поверхности стола равно длине пробирки l. Нить пережигают, и за время падения пробирки муха перелетает со дна в верхний конец пробирки. Определить время, за которое пробирка достигнет стола.
Решение. Ускорение центра масс системы определяется силами тяжести, действующими на пробирку и муху, и равно g. За время падения центр масс системы переместился на l/2. Отсюда время падения 
Задача 8. На нити, перекинутой через блок, подвешены два груза неравной массы (m2 > m1). Определить ускорение центра масс этой системы. Массой блока и нити пренебречь. [2]
Решение. Ускорение тяжелого груза направлено вниз и, как известно, равно 
Задача 9. В сосуде, наполненном водой плотности p, с ускорением а всплывает пузырек воздуха, объем которого V. Найдите силу давления со стороны сосуда на опору. Масса сосуда вместе с водой равна m. [1]
Решение. Будем рассматривать системы как совокупность сосуда с водой массой 



Задачи для самостоятельного решения.
Задача 10. С горы с уклоном a (


Ответ:
Задача 11. Человек, находящийся в лодке, переходит с носа на корму. На какое расстояние S переместится лодка длиной L, если масса человека m, а масса лодки M? Сопротивлением воды пренебречь.
Ответ:
Задача 12. На поверхности воды находится в покое лодка. Человек, находящийся в ней, переходит с кормы на нос. Как будет двигаться лодка, если сила сопротивления движению пропорциональна скорости лодки?
Ответ: Лодка сместится, а затем вернется в исходное положение.
Задача 13. На первоначально неподвижной тележке установлены два вертикальных цилиндрических сосуда, соединенных тонкой трубкой. Площадь сечения каждого сосуда S, расстояние между их осями l. Один из сосудов заполнен жидкостью плотности p. Кран на соединительной трубке открывают. Найдите скорость тележки в момент времени, когда скорость уровней жидкости равна v. Полная масса всей системы m. [1]
Ответ:
Задача 14. На тележке установлен цилиндрический сосуд с площадью сечения S, наполненный жидкостью плотности p. От сосуда параллельно полу отходит длинная и тонкая горизонтальная трубка, небольшой отрезок которой вблизи конца загнут по вертикали вниз. Расстояние от оси сосуда до отверстия трубки равно L. Уровень жидкости в сосуде опускается с ускорением а. Какой горизонтальной силой можно удержать тележку на месте? [1]
Ответ:
Литература.
1. Задачи по физике: Учеб. пособие/ И.И. Воробьев, П.И. Зубков, Г.А. Кутузова и др.; Под ред. О.Я. Савченко. ? 2-е изд., перераб. М.: Наука. Гл. ред. физ.-мат. лит. 1988. — 416 с.
2. Дмитриев С.Н., Васюков В.И., Струков Ю.А. Физика: Сборник задач для поступающих в вузы. Изд. 7-е, доп. М: Ориентир. 2005. – 312 с.
3. Методическое пособие для поступающих в вузы / Под. ред. Чешева Ю.В. М.: Физматкнига, 2006. – 288 с.
💥 Видео
Центростремительное ускорение. 9 класс.Скачать

Урок 80. Определение положения центра масс телаСкачать

Теорема о движении центра масс системы. Дикая теорема для решения олимпиадных задач по физикеСкачать

Центр масс. Теорема о движении центра масс. Видеоурок 16. Физика 10 классСкачать

Равновесие тел. Условие равновесия тел. Центр масс и центр тяжести. Практическая часть. 10 класс.Скачать

начертить окружность. Привести уравнение окружности к стандартному виду. Координаты центра и радиус.Скачать

Геометрия масс. Теорема о движении центра массСкачать

Центр массСкачать

Как Найти Радиус Сегмента на Потолке. Радиус Окружности По Хорде И Высоте СегментаСкачать