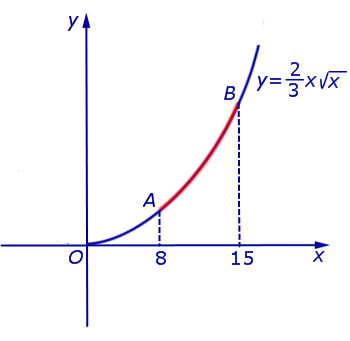
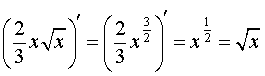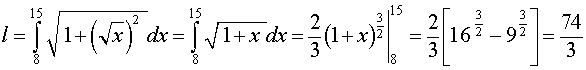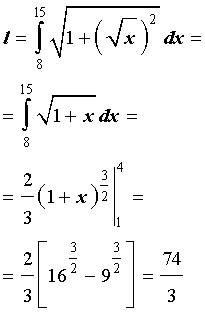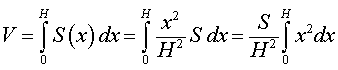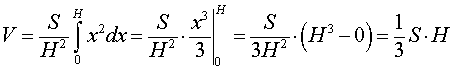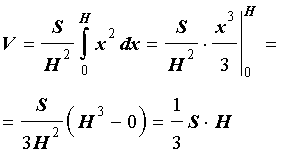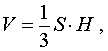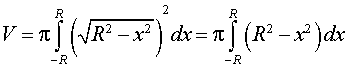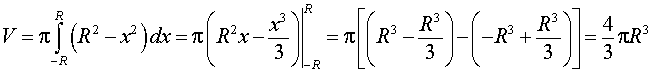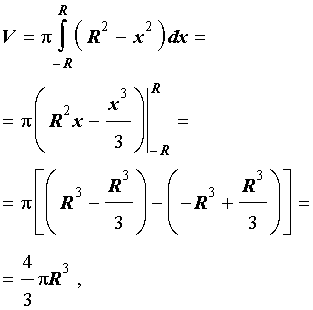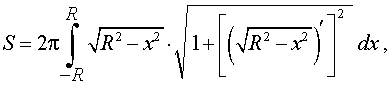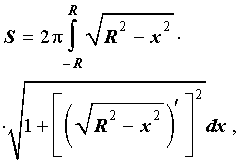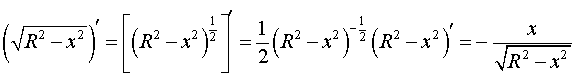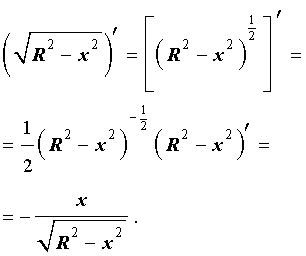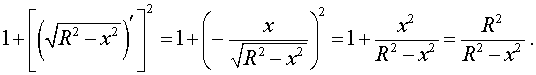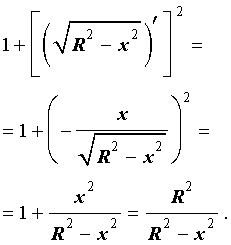Задачка это школьная, но, несмотря на то, почти 100% встретится в вашем курсе высшей математики. Поэтому со всей серьёзностью отнесёмся ко ВСЕМ примерам, и первое, что нужно сделать – это ознакомиться с Приложением Графики функций, чтобы освежить в памяти технику построения элементарных графиков. …Есть? Отлично! Типовая формулировка задания звучит так:
Пример 10
Вычислить площадь фигуры, ограниченной линиями 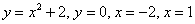
И первый важнейший этап решения состоит как раз в построении чертежа. При этом я рекомендую следующий порядок: сначала лучше построить все прямые (если они есть) и только потом – параболы, гиперболы, графики других функций.
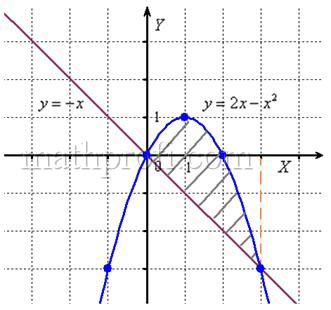
В нашей задаче: прямая 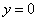
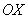
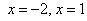
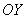
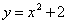
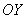
Искомую фигуру желательно штриховать:
Второй этап состоит в том, чтобы правильно составить и правильно вычислить определённый интеграл. На отрезке 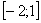
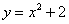
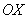
Ответ:
После того, как задание выполнено, полезно взглянуть на чертёж
и прикинуть, реалистичный ли получился ответ.
И мы «на глазок» подсчитываем количество заштрихованных клеточек – ну, примерно 9 наберётся, похоже на правду. Совершенно понятно, что если бы у нас получилось, скажем, 20 квадратных единиц, то, очевидно, где-то допущена ошибка – в построенную фигуру 20 клеток явно не вмещается, от силы десяток. Если ответ получился отрицательным, то задание тоже решено некорректно.
Пример 11
Вычислить площадь фигуры, ограниченной линиями 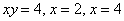
Быстренько разминаемся (обязательно!) и рассматриваем «зеркальную» ситуацию – когда криволинейная трапеция расположена под осью 
Пример 12
Вычислить площадь фигуры, ограниченной линиями 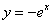
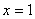
Решение: найдём несколько опорных точек для построения экспоненты: 
и выполним чертёж, получая фигуру площадью около двух клеток: 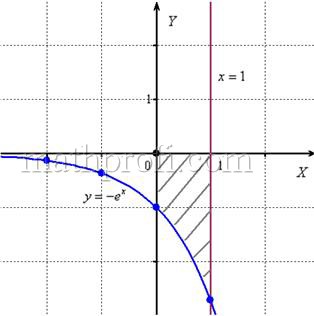
Если криволинейная трапеция расположена не выше оси 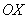
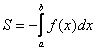
В данном случае:
Ответ: 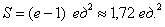
На практике чаще всего фигура расположена и в верхней и в нижней полуплоскости, а поэтому от простейших школьных задачек мы переходим к более содержательным примерам:
Пример 13
Найти площадь плоской фигуры, ограниченной линиями 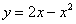
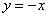
Решение: сначала нужно выполнить чертеж, при этом нас особо интересуют точки пересечения параболы 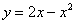
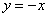
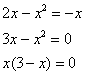
таким образом:
Достоинство аналитического способа состоит в его точности, а недостаток – в длительности (и в этом примере нам ещё повезло). Поэтому во многих задачах бывает выгоднее построить линии поточечно, при этом пределы интегрирования выясняются как бы «сами собой».
С прямой 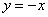
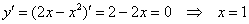
Выполним чертеж:
А теперь рабочая формула: если на отрезке 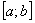
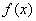
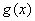
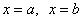
Здесь уже не надо думать, где расположена фигура – над осью или под осью, а, грубо говоря, важно, какой из двух графиков ВЫШЕ.
В нашем примере очевидно, что на отрезке 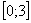
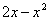
Завершение решения может выглядеть так:
На отрезке 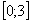
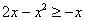
Ответ:
Следует отметить, что простые формулы, рассмотренные в начале параграфа – это частные случаи формулы 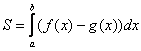
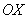
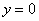
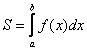
А сейчас пара типовых задач для самостоятельного решения
Пример 14
Найти площадь фигур, ограниченных линиями:
а) 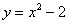
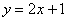
б) 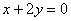
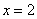
Решение с чертежами и краткими комментариями в конце книги
В ходе решения рассматриваемой задачи иногда случается забавный казус. Чертеж выполнен правильно, интеграл решён правильно, но по невнимательности… найдена площадь не той фигуры, именно так несколько раз ошибался ваш покорный слуга. Вот реальный случай из жизни:
Пример 15
Вычислить площадь фигуры, ограниченной линиями
Решение: выполним бесхитростный чертёж, 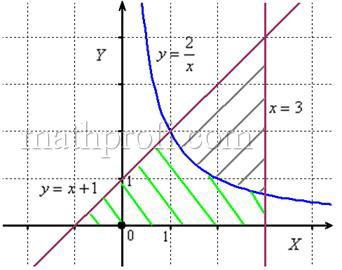
хитрость которого состоит в том, что искомая площадь заштрихована зелёным цветом (внимательно смотрИте на условие – чем ограничена фигура!). Но на практике по невнимательности нередко возникает «глюк», что нужно найти площадь фигуры, которая заштрихована серым цветом! Особое коварство состоит в том, что прямую 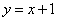
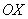
Этот пример ещё и полезен тем, что в нём площадь фигуры считается с помощью двух определённых интегралов. Действительно:
1) на отрезке 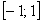
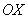
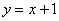
2) на отрезке 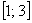
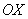
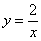
Совершенно понятно, что площади можно (и нужно) сложить:
Ответ:
И познавательный пример для самостоятельного решения:
Пример 16
Вычислить площадь фигуры, ограниченной линиями 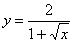
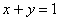
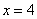
Итак, систематизируем важные моменты этой задачи:
На первом шаге ВНИМАТЕЛЬНО изучаем условие – КАКИЕ функции нам даны? Ошибки бывают даже здесь, в частности, арккотангенс 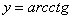
Далее следует ПРАВИЛЬНО выполнить чертёж. Сначала лучше построить прямые (если они есть), затем графики других функций (если они есть J). Последние во многих случаях выгоднее строить поточечно – найти несколько опорных точек и аккуратно соединить их линией.
Но здесь могут подстерегать следующие трудности. Во-первых, из чертежа не всегда понятны пределы интегрирования – так бывает, когда они дробные. На mathprofi.ru в соответствующей статье я рассмотрел пример с параболой 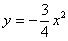
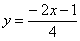
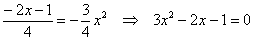
и находим его корни:
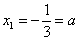
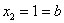
Во-вторых, не всегда понятен «внешний вид» линии, и функция 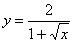
Ну и, конечно, я призываю вас повышать свои знания и навыки в графиках, в частности, приведу прямую ссылку на особо полезную статью:
http://mathprofi.ru/kak_postroit_grafik_funkcii_s_pomoshyu_preobrazovanii.html
После того, как чертёж построен, анализируем полученную фигуру – ещё раз окидываем взглядом предложенные функции и перепроверяем, ТА ЛИ это фигура. Затем анализируем её форму и расположение, бывает, что площадь достаточно сложнА и тогда её следует разделить на две, а то и на три части.
Составляем определённый интеграл или несколько интегралов по формуле 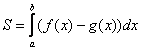
Решаем определённый интеграл (ы). При этом он может оказаться достаточно сложным, и тогда применяем поэтапный алгоритм: 1) находим первообразную и проверяем её дифференцированием, 2) используем формулу Ньютона-Лейбница.
Результат полезно проверить с помощью программного обеспечения / онлайн сервисов или просто «прикинуть» по чертежу по клеточкам. Но и то, и другое не всегда осуществимо, поэтому крайне внимательно относимся к каждому этапу решения!
Полную и свежую версию данного курса в pdf-формате ,
а также курсы по другим темам можно найти здесь.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
- Нахождение площади фигуры, ограниченной линиями y=f(x), x=g(y)
- Формула для вычисления площади фигуры, ограниченной линиями y=f(x) или x=g(y)
- Примеры вычисления площади фигуры, ограниченной линиями y=f(x) или x=g(y)
- Итоги
- Геометрические приложения определенного интеграла
- Формулы для вычисления площадей фигур на плоскости, длин дуг кривых на плоскости, площадей поверхностей тел вращения и объемов тел с помощью определенного интеграла
- Примеры решения задач на вычисление площадей фигур на плоскости
- Пример решения задачи на вычисление длины дуги кривой на плоскости
- Вывод формул для объема пирамиды и для объема шара
- Вывод формулы для площади сферы
- 📽️ Видео
Видео:Площадь треугольника с помощью интегралаСкачать

Нахождение площади фигуры, ограниченной линиями y=f(x), x=g(y)
В предыдущем разделе, посвященном разбору геометрического смысла определенного интеграла, мы получили ряд формул для вычисления площади криволинейной трапеции:
S ( G ) = ∫ a b f ( x ) d x для непрерывной и неотрицательной функции y = f ( x ) на отрезке [ a ; b ] ,
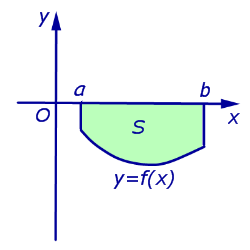
S ( G ) = — ∫ a b f ( x ) d x для непрерывной и неположительной функции y = f ( x ) на отрезке [ a ; b ] .
Эти формулы применимы для решения относительно простых задач. На деле же нам чаще придется работать с более сложными фигурами. В связи с этим, данный раздел мы посвятим разбору алгоритмов вычисления площади фигур, которые ограничены функциями в явном виде, т.е. как y = f ( x ) или x = g ( y ) .
Видео:Математика без Ху!ни. Определенные интегралы, часть 3. Площадь фигуры.Скачать

Формула для вычисления площади фигуры, ограниченной линиями y=f(x) или x=g(y)
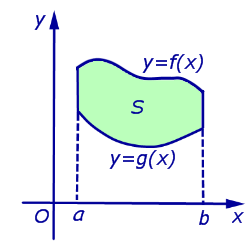
Пусть функции y = f 1 ( x ) и y = f 2 ( x ) определены и непрерывны на отрезке [ a ; b ] , причем f 1 ( x ) ≤ f 2 ( x ) для любого значения x из [ a ; b ] . Тогда формула для вычисления площади фигуры G , ограниченной линиями x = a , x = b , y = f 1 ( x ) и y = f 2 ( x ) будет иметь вид S ( G ) = ∫ a b f 2 ( x ) — f 1 ( x ) d x .
Похожая формула будет применима для площади фигуры, ограниченной линиями y = c , y = d , x = g 1 ( y ) и x = g 2 ( y ) : S ( G ) = ∫ c d ( g 2 ( y ) — g 1 ( y ) d y .
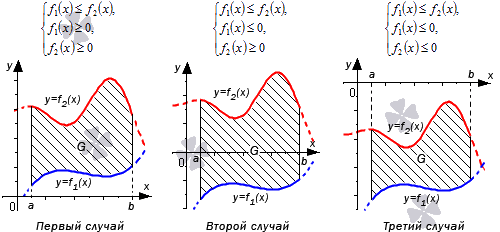
Разберем три случая, для которых формула будет справедлива.
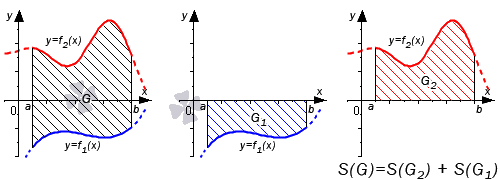
В первом случае, учитывая свойство аддитивности площади, сумма площадей исходной фигуры G и криволинейной трапеции G 1 равна площади фигуры G 2 . Это значит, что
Поэтому, S ( G ) = S ( G 2 ) — S ( G 1 ) = ∫ a b f 2 ( x ) d x — ∫ a b f 1 ( x ) d x = ∫ a b ( f 2 ( x ) — f 1 ( x ) ) d x .
Выполнить последний переход мы можем с использованием третьего свойства определенного интеграла.
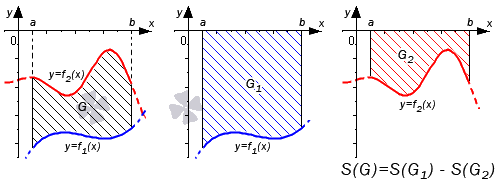
Во втором случае справедливо равенство: S ( G ) = S ( G 2 ) + S ( G 1 ) = ∫ a b f 2 ( x ) d x + — ∫ a b f 1 ( x ) d x = ∫ a b ( f 2 ( x ) — f 1 ( x ) ) d x
Графическая иллюстрация будет иметь вид:
Если обе функции неположительные, получаем: S ( G ) = S ( G 2 ) — S ( G 1 ) = — ∫ a b f 2 ( x ) d x — — ∫ a b f 1 ( x ) d x = ∫ a b ( f 2 ( x ) — f 1 ( x ) ) d x . Графическая иллюстрация будет иметь вид:
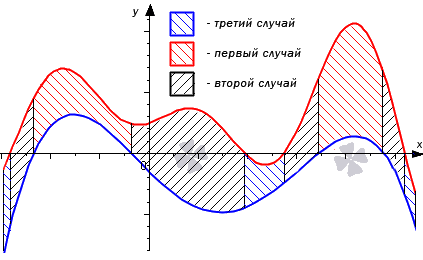
Перейдем к рассмотрению общего случая, когда y = f 1 ( x ) и y = f 2 ( x ) пересекают ось O x .
Точки пересечения мы обозначим как x i , i = 1 , 2 , . . . , n — 1 . Эти точки разбивают отрезок [ a ; b ] на n частей x i — 1 ; x i , i = 1 , 2 , . . . , n , где α = x 0 x 1 x 2 . . . x n — 1 x n = b . Фигуру G можно представить объединением фигур G i , i = 1 , 2 , . . . , n . Очевидно, что на своем интервале G i попадает под один из трех рассмотренных ранее случаев, поэтому их площади находятся как S ( G i ) = ∫ x i — 1 x i ( f 2 ( x ) — f 1 ( x ) ) d x , i = 1 , 2 , . . . , n
S ( G ) = ∑ i = 1 n S ( G i ) = ∑ i = 1 n ∫ x i x i f 2 ( x ) — f 1 ( x ) ) d x = = ∫ x 0 x n ( f 2 ( x ) — f ( x ) ) d x = ∫ a b f 2 ( x ) — f 1 ( x ) d x
Последний переход мы можем осуществить с использованием пятого свойства определенного интеграла.
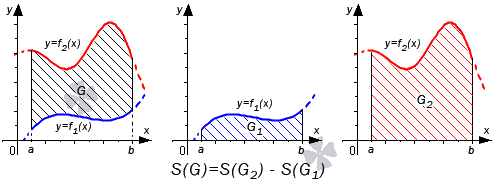
Проиллюстрируем на графике общий случай.
Формулу S ( G ) = ∫ a b f 2 ( x ) — f 1 ( x ) d x можно считать доказанной.
А теперь перейдем к разбору примеров вычисления площади фигур, которые ограничены линиями y = f ( x ) и x = g ( y ) .
Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Примеры вычисления площади фигуры, ограниченной линиями y=f(x) или x=g(y)
Рассмотрение любого из примеров мы будем начинать с построения графика. Изображение позволит нам представлять сложные фигуры как объединения более простых фигур. Если построение графиков и фигур на них вызывает у вас затруднения, можете изучить раздел об основных элементарных функциях, геометрическом преобразовании графиков функций, а также построению графиков во время исследования функции.
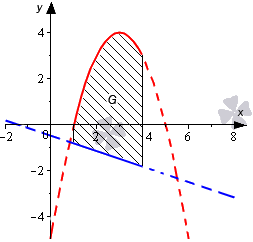
Необходимо определить площадь фигуры, которая ограничена параболой y = — x 2 + 6 x — 5 и прямыми линиями y = — 1 3 x — 1 2 , x = 1 , x = 4 .
Решение
Изобразим линии на графике в декартовой системе координат.
На отрезке [ 1 ; 4 ] график параболы y = — x 2 + 6 x — 5 расположен выше прямой y = — 1 3 x — 1 2 . В связи с этим, для получения ответа используем формулу, полученную ранее, а также способ вычисления определенного интеграла по формуле Ньютона-Лейбница:
S ( G ) = ∫ 1 4 — x 2 + 6 x — 5 — — 1 3 x — 1 2 d x = = ∫ 1 4 — x 2 + 19 3 x — 9 2 d x = — 1 3 x 3 + 19 6 x 2 — 9 2 x 1 4 = = — 1 3 · 4 3 + 19 6 · 4 2 — 9 2 · 4 — — 1 3 · 1 3 + 19 6 · 1 2 — 9 2 · 1 = = — 64 3 + 152 3 — 18 + 1 3 — 19 6 + 9 2 = 13
Ответ: S ( G ) = 13
Рассмотрим более сложный пример.
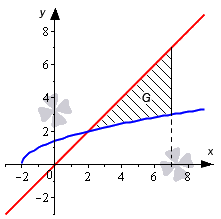
Необходимо вычислить площадь фигуры, которая ограничена линиями y = x + 2 , y = x , x = 7 .
Решение
В данном случае мы имеем только одну прямую линию, расположенную параллельно оси абсцисс. Это x = 7 . Это требует от нас найти второй предел интегрирования самостоятельно.
Построим график и нанесем на него линии, данные в условии задачи.
Имея график перед глазами, мы легко можем определить, что нижним пределом интегрирования будет абсцисса точки пересечения графика прямой y = x и полу параболы y = x + 2 . Для нахождения абсциссы используем равенства:
y = x + 2 О Д З : x ≥ — 2 x 2 = x + 2 2 x 2 — x — 2 = 0 D = ( — 1 ) 2 — 4 · 1 · ( — 2 ) = 9 x 1 = 1 + 9 2 = 2 ∈ О Д З x 2 = 1 — 9 2 = — 1 ∉ О Д З
Получается, что абсциссой точки пересечения является x = 2 .
Обращаем ваше внимание на тот факт, что в общем примере на чертеже линии y = x + 2 , y = x пересекаются в точке ( 2 ; 2 ) , поэтому такие подробные вычисления могут показаться излишними. Мы привели здесь такое подробное решение только потому, что в более сложных случаях решение может быть не таким очевидным. Это значит, что координаты пересечения линий лучше всегда вычислять аналитически.
На интервале [ 2 ; 7 ] график функции y = x расположен выше графика функции y = x + 2 . Применим формулу для вычисления площади:
S ( G ) = ∫ 2 7 ( x — x + 2 ) d x = x 2 2 — 2 3 · ( x + 2 ) 3 2 2 7 = = 7 2 2 — 2 3 · ( 7 + 2 ) 3 2 — 2 2 2 — 2 3 · 2 + 2 3 2 = = 49 2 — 18 — 2 + 16 3 = 59 6
Ответ: S ( G ) = 59 6
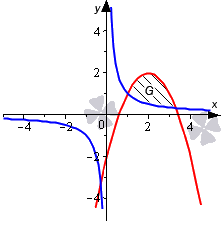
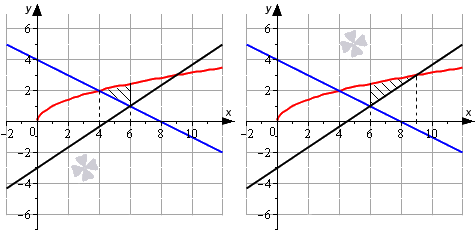
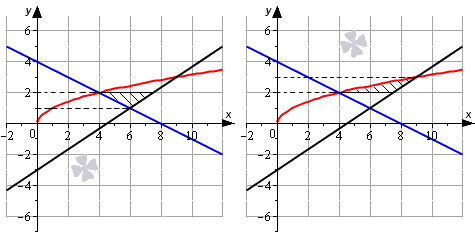
Необходимо вычислить площадь фигуры, которая ограничена графиками функций y = 1 x и y = — x 2 + 4 x — 2 .
Решение
Нанесем линии на график.
Определимся с пределами интегрирования. Для этого определим координаты точек пересечения линий, приравняв выражения 1 x и — x 2 + 4 x — 2 . При условии, что x не равно нулю, равенство 1 x = — x 2 + 4 x — 2 становится эквивалентным уравнению третьей степени — x 3 + 4 x 2 — 2 x — 1 = 0 с целыми коэффициентами. Освежить в памяти алгоритм по решению таких уравнений мы можете, обратившись к разделу «Решение кубических уравнений».
Корнем этого уравнения является х = 1 : — 1 3 + 4 · 1 2 — 2 · 1 — 1 = 0 .
Разделив выражение — x 3 + 4 x 2 — 2 x — 1 на двучлен x — 1 , получаем: — x 3 + 4 x 2 — 2 x — 1 ⇔ — ( x — 1 ) ( x 2 — 3 x — 1 ) = 0
Оставшиеся корни мы можем найти из уравнения x 2 — 3 x — 1 = 0 :
x 2 — 3 x — 1 = 0 D = ( — 3 ) 2 — 4 · 1 · ( — 1 ) = 13 x 1 = 3 + 13 2 ≈ 3 . 3 ; x 2 = 3 — 13 2 ≈ — 0 . 3
Мы нашли интервал x ∈ 1 ; 3 + 13 2 , на котором фигура G заключена выше синей и ниже красной линии. Это помогает нам определить площадь фигуры:
S ( G ) = ∫ 1 3 + 13 2 — x 2 + 4 x — 2 — 1 x d x = — x 3 3 + 2 x 2 — 2 x — ln x 1 3 + 13 2 = = — 3 + 13 2 3 3 + 2 · 3 + 13 2 2 — 2 · 3 + 13 2 — ln 3 + 13 2 — — — 1 3 3 + 2 · 1 2 — 2 · 1 — ln 1 = 7 + 13 3 — ln 3 + 13 2
Ответ: S ( G ) = 7 + 13 3 — ln 3 + 13 2
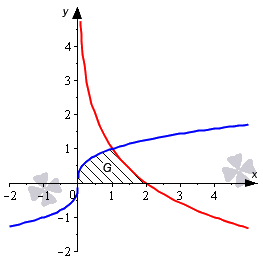
Необходимо вычислить площадь фигуры, которая ограничена кривыми y = x 3 , y = — log 2 x + 1 и осью абсцисс.
Решение
Нанесем все линии на график. Мы можем получить график функции y = — log 2 x + 1 из графика y = log 2 x , если расположим его симметрично относительно оси абсцисс и поднимем на одну единицу вверх. Уравнение оси абсцисс у = 0 .
Обозначим точки пересечения линий.
Как видно из рисунка, графики функций y = x 3 и y = 0 пересекаются в точке ( 0 ; 0 ) . Так получается потому, что х = 0 является единственным действительным корнем уравнения x 3 = 0 .
x = 2 является единственным корнем уравнения — log 2 x + 1 = 0 , поэтому графики функций y = — log 2 x + 1 и y = 0 пересекаются в точке ( 2 ; 0 ) .
x = 1 является единственным корнем уравнения x 3 = — log 2 x + 1 . В связи с этим графики функций y = x 3 и y = — log 2 x + 1 пересекаются в точке ( 1 ; 1 ) . Последнее утверждение может быть неочевидным, но уравнение x 3 = — log 2 x + 1 не может иметь более одного корня, так как функция y = x 3 является строго возрастающей, а функция y = — log 2 x + 1 строго убывающей.
Дальнейшее решение предполагает несколько вариантов.
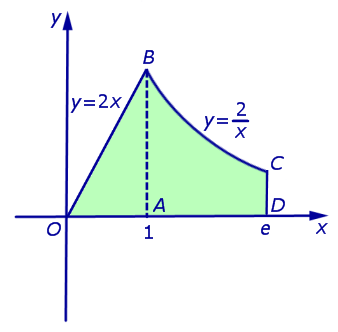
Вариант №1
Фигуру G мы можем представить как сумму двух криволинейных трапеций, расположенных выше оси абсцисс, первая из которых располагается ниже средней линии на отрезке x ∈ 0 ; 1 , а вторая ниже красной линии на отрезке x ∈ 1 ; 2 . Это значит, что площадь будет равна S ( G ) = ∫ 0 1 x 3 d x + ∫ 1 2 ( — log 2 x + 1 ) d x .
Вариант №2
Фигуру G можно представить как разность двух фигур, первая из которых расположена выше оси абсцисс и ниже синей линии на отрезке x ∈ 0 ; 2 , а вторая между красной и синей линиями на отрезке x ∈ 1 ; 2 . Это позволяет нам найти площадь следующим образом:
S ( G ) = ∫ 0 2 x 3 d x — ∫ 1 2 x 3 — ( — log 2 x + 1 ) d x
В этом случае для нахождения площади придется использовать формулу вида S ( G ) = ∫ c d ( g 2 ( y ) — g 1 ( y ) ) d y . Фактически, линии, которые ограничивают фигуру, можно представить в виде функций от аргумента y .
Разрешим уравнения y = x 3 и — log 2 x + 1 относительно x :
y = x 3 ⇒ x = y 3 y = — log 2 x + 1 ⇒ log 2 x = 1 — y ⇒ x = 2 1 — y
Получим искомую площадь:
S ( G ) = ∫ 0 1 ( 2 1 — y — y 3 ) d y = — 2 1 — y ln 2 — y 4 4 0 1 = = — 2 1 — 1 ln 2 — 1 4 4 — — 2 1 — 0 ln 2 — 0 4 4 = — 1 ln 2 — 1 4 + 2 ln 2 = 1 ln 2 — 1 4
Ответ: S ( G ) = 1 ln 2 — 1 4
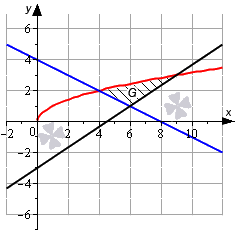
Необходимо вычислить площадь фигуры, которая ограничена линиями y = x , y = 2 3 x — 3 , y = — 1 2 x + 4 .
Решение
Красной линией нанесем на график линию, заданную функцией y = x . Синим цветом нанесем линию y = — 1 2 x + 4 , черным цветом обозначим линию y = 2 3 x — 3 .
Отметим точки пересечения.
Найдем точки пересечения графиков функций y = x и y = — 1 2 x + 4 :
x = — 1 2 x + 4 О Д З : x ≥ 0 x = — 1 2 x + 4 2 ⇒ x = 1 4 x 2 — 4 x + 16 ⇔ x 2 — 20 x + 64 = 0 D = ( — 20 ) 2 — 4 · 1 · 64 = 144 x 1 = 20 + 144 2 = 16 ; x 2 = 20 — 144 2 = 4 П р о в е р к а : x 1 = 16 = 4 , — 1 2 x 1 + 4 = — 1 2 · 16 + 4 = — 4 ⇒ x 1 = 16 н е я в л я е т с я р е ш е н и е м у р а в н е н и я x 2 = 4 = 2 , — 1 2 x 2 + 4 = — 1 2 · 4 + 4 = 2 ⇒ x 2 = 4 я в л я е т с я р е ш е н и е м у р а в н и н и я ⇒ ( 4 ; 2 ) т о ч к а п е р е с е ч е н и я y = x и y = — 1 2 x + 4
Найдем точку пересечения графиков функций y = x и y = 2 3 x — 3 :
x = 2 3 x — 3 О Д З : x ≥ 0 x = 2 3 x — 3 2 ⇔ x = 4 9 x 2 — 4 x + 9 ⇔ 4 x 2 — 45 x + 81 = 0 D = ( — 45 ) 2 — 4 · 4 · 81 = 729 x 1 = 45 + 729 8 = 9 , x 2 45 — 729 8 = 9 4 П р о в е р к а : x 1 = 9 = 3 , 2 3 x 1 — 3 = 2 3 · 9 — 3 = 3 ⇒ x 1 = 9 я в л я е т с я р е ш е н и е м у р а в н е н и я ⇒ ( 9 ; 3 ) т о ч к а п е р е с е ч а н и я y = x и y = 2 3 x — 3 x 2 = 9 4 = 3 2 , 2 3 x 1 — 3 = 2 3 · 9 4 — 3 = — 3 2 ⇒ x 2 = 9 4 н е я в л я е т с я р е ш е н и е м у р а в н е н и я
Найдем точку пересечения линий y = — 1 2 x + 4 и y = 2 3 x — 3 :
— 1 2 x + 4 = 2 3 x — 3 ⇔ — 3 x + 24 = 4 x — 18 ⇔ 7 x = 42 ⇔ x = 6 — 1 2 · 6 + 4 = 2 3 · 6 — 3 = 1 ⇒ ( 6 ; 1 ) т о ч к а п е р е с е ч е н и я y = — 1 2 x + 4 и y = 2 3 x — 3
Дальше мы можем продолжить вычисления двумя способами.
Способ №1
Представим площадь искомой фигуры как сумму площадей отдельных фигур.
Тогда площадь фигуры равна:
S ( G ) = ∫ 4 6 x — — 1 2 x + 4 d x + ∫ 6 9 x — 2 3 x — 3 d x = = 2 3 x 3 2 + x 2 4 — 4 x 4 6 + 2 3 x 3 2 — x 2 3 + 3 x 6 9 = = 2 3 · 6 3 2 + 6 2 4 — 4 · 6 — 2 3 · 4 3 2 + 4 2 4 — 4 · 4 + + 2 3 · 9 3 2 — 9 2 3 + 3 · 9 — 2 3 · 6 3 2 — 6 2 3 + 3 · 6 = = — 25 3 + 4 6 + — 4 6 + 12 = 11 3
Способ №2
Площадь исходной фигуры можно представить как сумму двух других фигур.
Тогда решим уравнение линии относительно x , а только после этого применим формулу вычисления площади фигуры.
y = x ⇒ x = y 2 к р а с н а я л и н и я y = 2 3 x — 3 ⇒ x = 3 2 y + 9 2 ч е р н а я л и н и я y = — 1 2 x + 4 ⇒ x = — 2 y + 8 с и н я я л и н и я
Таким образом, площадь равна:
S ( G ) = ∫ 1 2 3 2 y + 9 2 — — 2 y + 8 d y + ∫ 2 3 3 2 y + 9 2 — y 2 d y = = ∫ 1 2 7 2 y — 7 2 d y + ∫ 2 3 3 2 y + 9 2 — y 2 d y = = 7 4 y 2 — 7 4 y 1 2 + — y 3 3 + 3 y 2 4 + 9 2 y 2 3 = 7 4 · 2 2 — 7 4 · 2 — 7 4 · 1 2 — 7 4 · 1 + + — 3 3 3 + 3 · 3 2 4 + 9 2 · 3 — — 2 3 3 + 3 · 2 2 4 + 9 2 · 2 = = 7 4 + 23 12 = 11 3
Как видите, значения совпадают.
Ответ: S ( G ) = 11 3
Видео:Найти площадь фигуры, ограниченной линиями. Пример 1.Скачать
Итоги
Для нахождения площади фигуры, которая ограничена заданными линиями нам необходимо построить линии на плоскости, найти точки их пересечения, применить формулу для нахождения площади. В данном разделе мы рассмотрели наиболее часто встречающиеся варианты задач.
Видео:Корнеев С.А. - Комбинаторика и сложность вычислений - 13. Вычисление биномиальных коэффициентовСкачать

Геометрические приложения определенного интеграла
 Формулы для вычисления площадей фигур на плоскости, длин дуг кривых на плоскости, площадей поверхностей тел вращения и объемов тел с помощью определенного интеграла Формулы для вычисления площадей фигур на плоскости, длин дуг кривых на плоскости, площадей поверхностей тел вращения и объемов тел с помощью определенного интеграла |
 Примеры решения задач на вычисление площадей фигур на плоскости Примеры решения задач на вычисление площадей фигур на плоскости |
 Пример решения задачи на вычисление длины дуги кривой на плоскости Пример решения задачи на вычисление длины дуги кривой на плоскости |
 Вывод формул для объема пирамиды и для объема шара Вывод формул для объема пирамиды и для объема шара |
 Вывод формулы для площади сферы Вывод формулы для площади сферы |
Видео:9 класс, 12 урок, Теорема о площади треугольникаСкачать

Формулы для вычисления площадей фигур на плоскости, длин дуг кривых на плоскости, площадей поверхностей тел вращения и объемов тел с помощью определенного интеграла
В данном разделе справочника приведена таблица, содержащая формулы, с помощью которых можно вычислить:
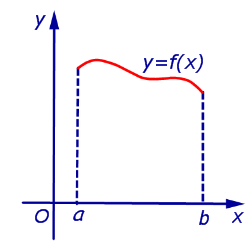
Площади криволинейных трапеций различного вида (площади фигур, ограниченных графиками функций);
Длины дуг кривых на плоскости;
Объемы тел, если известны площади их поперечных сечений;
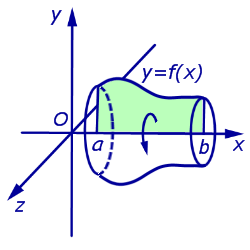
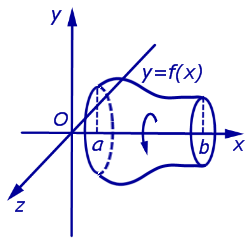
Объемы тел, полученных при вращении криволинейных трапеций вокруг оси абсцисс Ox ;
Площади поверхностей тел, полученных при вращении графиков функций вокруг оси абсцисс Ox .
| Рисунок | Формула | Описание | |||||||
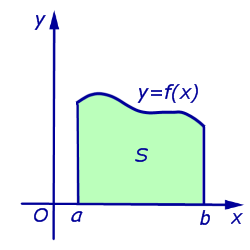 | 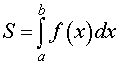 | ||||||||
 |  | ||||||||
 | 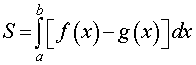 | ||||||||
 | 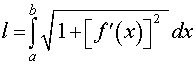 | ||||||||
 | 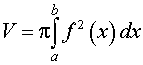 | ||||||||
 | 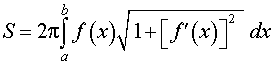 |
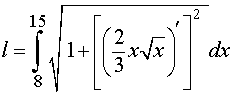 | (1) |
Подставим найденную производную в формулу (1), а затем вычислим полученные интегралы при помощи таблицы неопределенных интегралов и формулы Ньютона — Лейбница:
Ответ .
Видео:Криволинейная трапеция и ее площадь. 11 класс.Скачать

Вывод формул для объема пирамиды и для объема шара
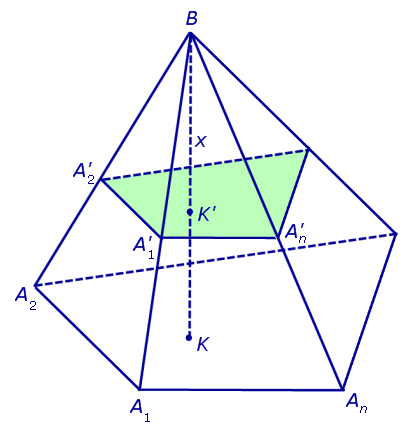
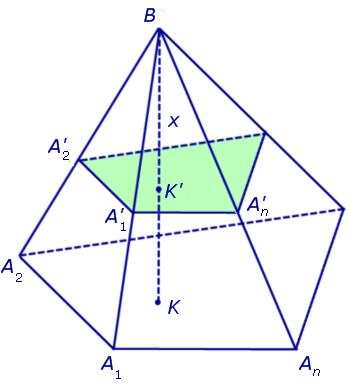
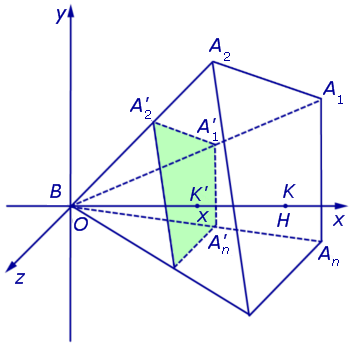
Решение . Рассмотрим произвольную n — угольную пирамиду BA1A2 . An с вершиной B, высота BK которой равна H, а площадь основания A1A2 . An равна S. Обозначим через S (x) площадь сечения 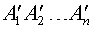
Поскольку многоугольники 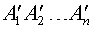
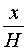
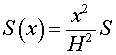 | (2) |
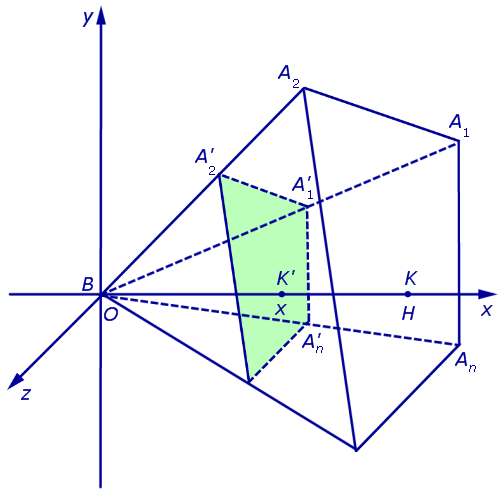
Рассмотрим теперь в пространстве систему координат Oxyz и расположим нашу пирамиду BA1A2 . An так, чтобы ее вершина B совпала с началом координат O, а высота пирамиды BK оказалась лежащей на оси Ox (рис. 5).
Тогда сечение 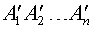
Итак, мы получили формулу для объема пирамиды
котрой пользовались в различных разделах справочника.
Замечание . Совершенно аналогично выводится формула для объема конуса. Формулы для объема прямой призмы объема прямой призмы и для объема цилиндра вывести таким способом еще проще, поскольку у них все сечения, перпендикулярные высоте, равны между собой. Мы рекомендуем провести эти выводы читателю самостоятельно в качестве полезного упражнения.
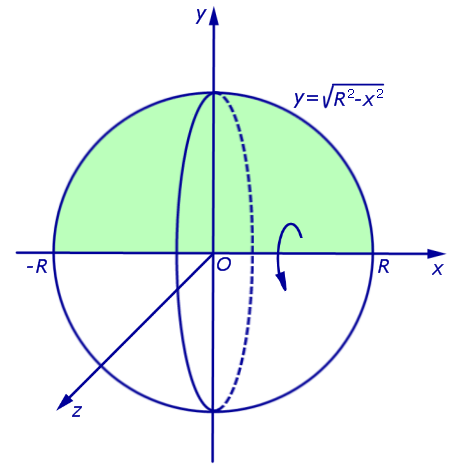
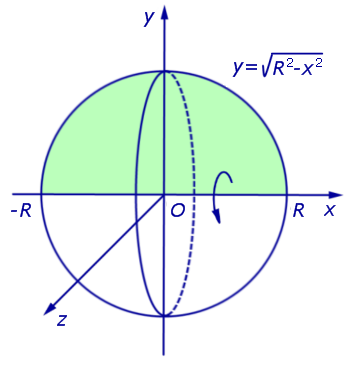
Пример 5 . Вывести формулу для объема шара радиуса R, воспользовавшись формулой для вычисления объема тела вращения.
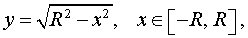 | (3) |
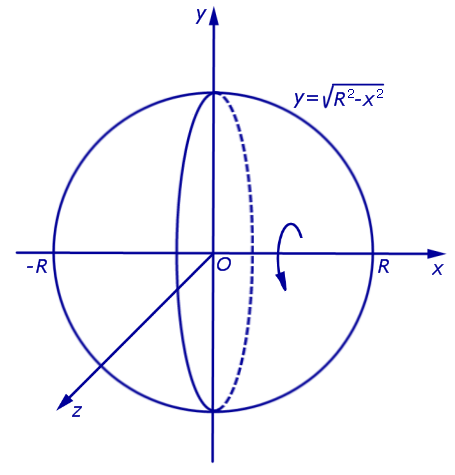
графиком которой является верхняя полуокружность радиуса R с центром в начале координат O. Шар радиуса R получается в результате вращения вокруг оси Ox криволинейной трапеции, ограниченной сверху графиком функции (3) и ограниченной снизу отрезком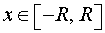
что и должно было получиться.
Видео:Интегралы №12 Вычисление площадейСкачать

Вывод формулы для площади сферы
Решение . Снова рассмотрим функцию
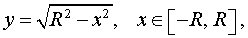 | (4) |
графиком которой является верхняя полуокружность радиуса R с центром в начале координат O (рис. 7).
Поскольку сфера радиуса R получается в результате вращения вокруг оси Ox графика функции (4), то в соответствии с формулой для вычисления площади поверхности тела вращения получаем
Подставим найденную производную в выражение, стоящее под знаком квадратного корня:
Таким образом, подынтегральная функция принимает вид:
📽️ Видео
Определённый интеграл. ПлощадьСкачать
Найдите площадь треугольника на рисунке ★ Два способа решенияСкачать

Найти площадь фигуры, ограниченной линиями. Пример 5.Скачать

Определенный интеграл. 11 класс.Скачать

Как удивить учителя математикиСкачать

Геометрия 8 класс (Урок№10 - Площадь треугольника.)Скачать

Площадь фигуры через двойной интеграл в полярных координатахСкачать

Как найти площадь этого треугольника, не зная формулы?Скачать

Площадь сферы внутри цилиндра. Поверхностный интегралСкачать

8 класс, 14 урок, Площадь треугольникаСкачать

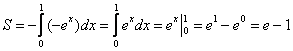
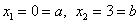
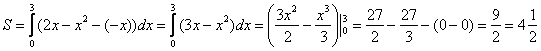
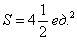
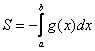
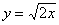
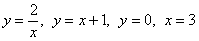
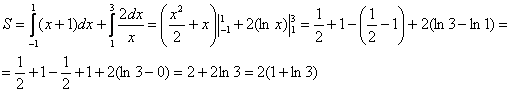
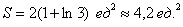

 ,
,
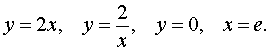
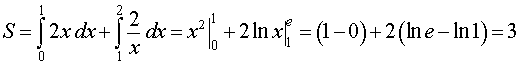
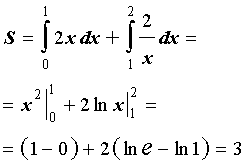
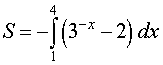 .
.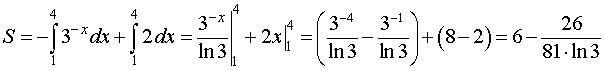
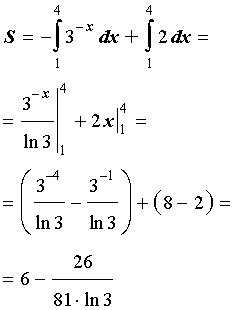
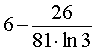 .
.
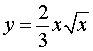 , 8 .
, 8 .