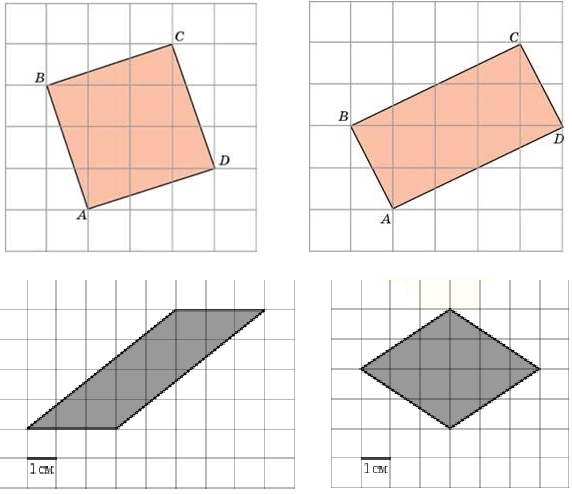
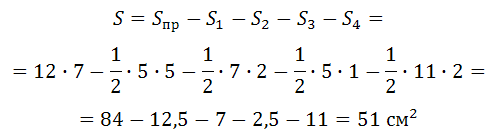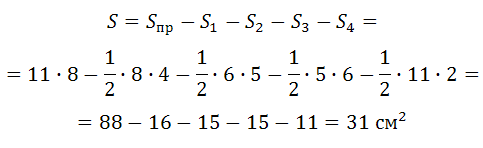Как найти площадь произвольного четырехугольника по клеткам (7 видео)

Площадь четырёхугольника на клетчатой бумаге

Площадь четырёхугольника на клетчатой бумаге. В статье « Нахождение площади треугольник а » я обещал рассмотреть задачи на вычисление площади четырёхугольника, построенного на листе в клетку. Как вы знаете, к четырёхугольникам относятся: прямоугольник , квадрат , параллелограмм , трапеция , ромб , а также произвольный четырёхугольник (выпуклый или вогнутый).

Мы с вами рассмотрим единый подход к решению всех типов таких заданий. Вот примеры рисунков из интересующих нас задач:

Фигуры построенные на листе в клетку (1×1 см)

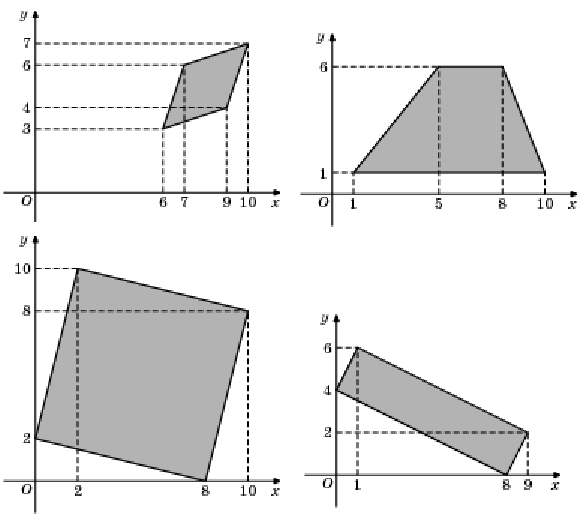
Фигуры построенные на координатной плоскости

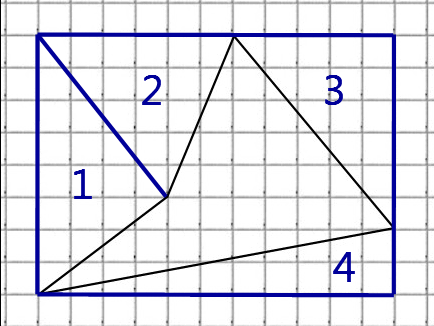
Запомните! Вокруг любого выпуклого четырёхугольника мы можем описать прямоугольник. А далее для решения необходимо воспользоваться всего двумя формулами: площади прямоугольника и площади треугольника.

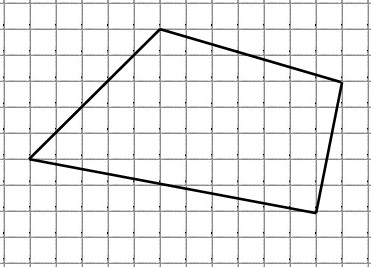
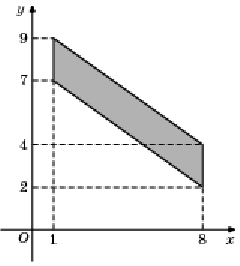
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

Около данного четырёхугольника описываем прямоугольник:

Из площади построенного прямоугольника вычтем площади четырёх прямоугольных треугольников:

Рассмотрим пример вогнутого четырёхугольника:

Найдите площадь четырёхугольника , изображенного на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

Также описываем прямоугольник, но здесь ещё строим дополнительный отрезок, соединяющий левый верхний угол прямоугольника с вогнутым углом данного четырёхугольника:

Из площади построенного прямоугольника вычтем площади четырёх треугольников:

Если четырёхугольник задан на координатной плоскости, то его легко можно построить на листе в клетку по заданным координатам вершин и применить изложенный выше подход к решению.

Конечно, данный способ нерационален абсолютно для всех задач. Но в вашем арсенале он быть должен, и им владеть необходимо, его удобно использовать во многих задачах

Например, для нахождения представленного четырёхугольника

целесообразно воспользоваться формулой площади параллелограмма, где основание будет равно 2, а высота 7. Но и представленным способом её также решать можно .

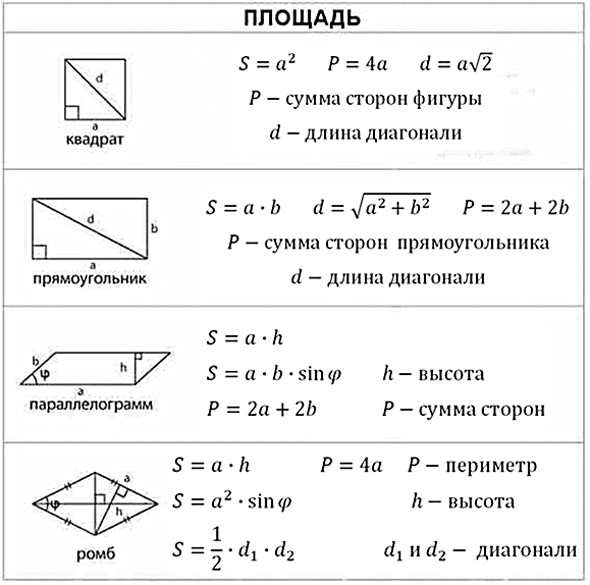
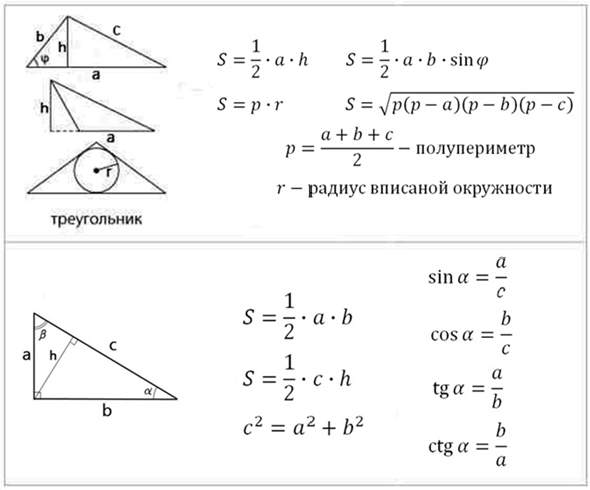
Напомню формулы площадей фигур, которые необходимо знать:

На этом всё. Надеюсь, информация была полезной. В будущем рассмотрим с вами задачи на нахождение площади круга, площади части круга и другие, где используются формулы площади круга и окружности. Также есть ещё один интересный приём, который целесообразно использовать для нахождение площади четырёхугольников вида (взяты из прототипов задач):

Содержание

Геометрия. Применение формул. Задача 5 Базового ЕГЭ по математике
Как найти площадь произвольного четырехугольника по клеткам
Вычисление площадей фигур на клетчатой бумаге разными способами
📹 Видео

Видео:Самый простой способ нахождения площадиСкачать

Геометрия. Применение формул. Задача 5 Базового ЕГЭ по математике

Чтобы уверенно решать задачи по геометрии — даже такие простые — необходимо выучить основные понятия и формулы.

Это формулы площадей фигур — треугольника (5 формул), параллелограмма, ромба, прямоугольника, произвольного четырехугольника, а также круга. Формулы для длины окружности, длины дуги и площади сектора. Для средней линии треугольника и средней линии трапеции.

Надо знать, что такое центральный и вписанный угол. Знать основные тригонометрические соотношения. В общем, учите основы планиметрии.

Больше полезных формул — в нашем ЕГЭ-Справочнике.

В этой статье — основные типы заданий №5 Базового ЕГЭ по математике. Задачи взяты из Банка заданий ФИПИ.

Вычисление длин отрезков, величин углов и площадей фигур по формулам

1. На клетчатой бумаге с размером клетки изображена трапеция. Найдите длину средней линии этой трапеции.

Средняя линия трапеции равна полусумме её оснований:

2. Найдите величину угла ABC. Ответ дайте в градусах.

Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Соединим точки А и С с центром окружности и проведем диаметры через точки А и С. Видим, что величина центрального угла АОС равна Тогда

3. Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на

Проведем из точки В перпендикуляр к прямой ОА. Из прямоугольного треугольника ОВС по теореме Пифагора:

Осталось умножить найденное значение синуса на

4. Найдите площадь ромба, изображенного на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.

Самый простой способ — воспользоваться формулой площади ромба, выраженной через его диагонали:

, где и — диагонали.

Получим:

5. Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.

Площадь трапеции равна произведению полусуммы оснований на высоту:

Основания нашей трапеции равны 4 и 8, а высота равна боковой стороне (поскольку трапеция прямоугольная), то есть 3 см. Площадь трапеции

Нахождение площадей многоугольников сложной формы

А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ и на авторских задачах.

6. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.

Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .

7. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.

Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .

Многие репетиторы рекомендуют в таких задачах пользоваться формулой Пика. В ней нет необходимости, однако эта формула довольно интересна.

Согласно формуле Пика, площадь многоугольника равна В+Г/2-1

где В — количество узлов внутри многоугольника, а Г — количество узлов на границе многоугольника.

Узлами здесь названы точки, в которых пересекаются линии нашей клетчатой бумаги.

Посмотрим, как решается задача 7 с помощью формулы Пика:

Синим на рисунке отмечены узлы внутри треугольника. Зеленым — узлы на границе.

Аккуратно посчитав те и другие, получим, что В = 9, Г = 5, и площадь фигуры равна S = 9 + 5/2 — 1 = 10,5.

Выбирайте — какой способ вам больше нравится.

8. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки

Такой четырехугольник получится, если от квадрата размером отрезать 2 прямоугольника и 4 треугольника. Найдите их на рисунке.

Площадь каждого из больших треугольников равна

Площадь каждого из маленьких треугольников равна

Тогда площадь четырехугольника

9. Авторская задача. Найдите площадь закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки

На рисунке изображен ромб с вырезанным из него квадратом.

Площадь ромба равна половине произведения его диагоналей.

Площадь вырезанного квадрата равна 4.

Площадь фигуры равна 36 — 4 = 32.

Площадь круга, длина окружности, площадь части круга

Длина дуги во столько раз меньше длины окружности, во сколько раз ее градусная мера меньше, чем полный круг, то есть 360 градусов.

Площадь сектора во столько раз меньше площади всего круга, во сколько раз его градусная мера меньше, чем полный круг, то есть 360 градусов.

10. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .

На этом рисунке мы видим часть круга. Площадь всего круга равна , так как . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.

11. На клетчатой бумаге нарисован круг площадью 2,8. Найдите площадь закрашенного сектора.

На рисунке изображен сектор, то есть часть круга. Но какая же это часть? Это четверть круга и еще круга, то есть круга.

Значит, нам надо умножить площадь круга на . Получим:

12. На клетчатой бумаге изображены два круга. Площадь внутреннего круга равна 9. Найдите площадь закрашенной фигуры.

Площадь фигуры равна разности площадей двух кругов, один из которых расположен внутри другого. По условию, площадь внутреннего круга равна 9. Радиус внешнего круга относится к радиусу внутреннего как 4 к 3. Площадь круга равна , то есть пропорциональна квадрату радиуса. Значит, площадь внешнего круга в раза больше площади внутреннего и равна 16. Тогда площадь фигуры равна 16 — 9 = 7.

Задачи на координатной плоскости

13. Найдите площадь четырехугольника, вершины которого имеют координаты (4;2), (8;4), (6;8), (2;6).

Заметим, что этот четырехугольник — квадрат. Сторона квадрата a является гипотенузой прямоугольного треугольника с катетами, равными 2 и 4. Тогда

14. Найдите площадь четырехугольника, вершины которого имеют координаты

На рисунке изображен параллелограмм (четырехугольник, имеющий две пары параллельных сторон). Площадь параллелограмма равна произведению основания на высоту. Основание равно 2, высота 8, площадь равна 16.

Видео:Найдите площадь треугольника изображенного на клетчатой бумаге с размером клетки 1х1 см.Скачать

Как найти площадь произвольного четырехугольника по клеткам

Видео:Площадь четырёхугольника на клетчатой бумагеСкачать

Вычисление площадей фигур на клетчатой бумаге разными способами

Автор работы награжден дипломом победителя II степени

Ещё в начальной школе мы освоили формулы нахождения площадей прямоугольника S = a • b, квадрата S = a2 и прямоугольного треугольника

При изучении математики в 5 классе мы тоже применяли эти формулы для вычисления площадей фигур. А также освоили основные свойства площадей: равные фигуры имеют равные площади; площадь фигуры равна сумме площадей её частей. В учебнике по математике для 5 класса есть задачи на клетчатой бумаге на нахождение площадей фигур. [1]

Мне стало очень интересно, какие способы решения таких задач существуют. При изучении литературы выявилось, что их достаточное количество. Я решила изучить их и проверить какой из них самый результативный, т.е. малозатратный по времени и дает безошибочный результат.

Проблема: Существует ли самый результативный способ нахождения площади фигуры на клетчатой бумаге?

Гипотеза: Самым эффективным способом вычисления площадей на клетчатой бумаге будет способ по формуле Пика.

Цель работы: Изучить способы решения задач на клетчатой бумаге и выбрать самый наилучший.

Изучить литературу по теме исследования.
Выбрать и изучить способы нахождения площадей фигур на клетчатой бумаге.
Подобрать задачи.
Провести эксперимент.
Сделать выводы.

Объект исследования: фигуры на клетчатой бумаге.

Предмет исследования: площадь фигур.

1) теоретический – изучение литературы;

2) эмпирический – эксперимент, анализ, сравнение;

3) математический – построение таблиц, вычисления.

Актуальность данной темы выбрана желанием показать разнообразие способов решения одной задачи. При решении олимпиадных задач я часто находилась в затруднении при встрече с задачами на клетчатой бумаге. А увидев такие задачи в КИМах ЕГЭ, ОГЭ приняла решение исследовать задачи на клетчатой бумаге и помочь выпускникам освоить их, чтобы как можно меньше времени тратить на выполнение таких заданий.

Рассмотрим основные способы решения таких задач в исследовательской работе.

2.1 Площадь фигуры как сумма площадей её частей

Задача 1. Найдём площадь фигуры АВСD (см.рис.1). Если клетки размером 1х1см.

Разобьем фигуру АВСD на части (1 и 2).

По свойству площадей:

S = S1 + S2 = (2•3):2 + 3•2 = 3 + 6 = 9 см²

Задача 2. Найдём площадь фигуры АВСD (см.рис.2). Если клетки размером 1х1см.

Разобьем фигуру АВСD на части (1, 2, 3 и 4).

По свойству площадей:

S = S1 + S2 + S3 + S4 =

= 2 + 1,5 + 1 + 1 = 5,5 см²

Задача 3. Найдём площадь фигуры АВСD (см. рис.3). Если клетки размером 1х1см.

Разобьем фигуру АВСD на части (1, 2 и 3).

По свойству площадей:

S = S1 + S2 + S3 = (1•4):2 + (3•3):2 + (1•3):2 = 2 + 4,5 + 1,5 = 8 см²

2.1 Площадь фигуры как часть площади прямоугольника

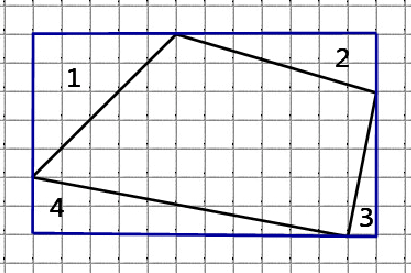
Задача 4. Найдём площадь фигуры АВСD (см. рис.4). Если клетки размером 1х1см.

Опишем около фигуры АВСD прямоугольник.

Из площади прямоугольника (в данном случае это квадрат) вычтем площади полученных простых фигур (1, 2, 3 и 4):

S = Sпр – S1 – S2 – S3 – S4 =

= 4•4 – (3•1):2 – (3•1):2 – (3•1):2 – (3•1):2 =

=16 – 1,5 – 1,5 – 1,5 – 1,5 = 10 см2. Ответ: 10 см²

Задача 5. Найдём площадь фигуры АВСD (см. рис.5). Если клетки размером 1х1см.

Опишем около фигуры АВСD прямоугольник.

Из площади прямоугольника (в данном случае это квадрат) вычтем площади полученных простых фигур (1, 2 и 3):

S = Sпр – S1 – S2 – S3 =

= 4•4 – (4•4):2 – (2•1):2 – (2•1):2 = 16 – 8 – 1 – 1 =

= 6 см². Ответ: 6 см²

Задача 6. Найдём площадь фигуры АВСD (см.рис.6). Если клетки размером 1х1см.

Опишем около фигуры АВСD прямоугольник.
Из площади прямоугольника вычтем площади полученных простых фигур (1, 2, 3 и 4):

S = Sпр – S1 – S2 – S3 – S4 =

= 3•6 – (4•1):2 – (2•2):2 – (4•1):2 – (2•2):2 =

= 18 – 2 – 2 – 2 – 2 = 10 см². Ответ: 10 см²

2.3 Формула Пика

Линии, идущие по сторонам клеток, образуют сетку, а вершины клеток – узлы этой сетки.

Нарисуем на листе многоугольник с вершинами в узлах (рис. 7) и найдем его площадь. [2]

Оказывается площади многоугольников, вершины которых расположены в узлах сетки, можно проще: есть формула, связывающая их площадь с количеством узлов, лежащих внутри и на границе многоугольника.

Пусть АВСD – прямоугольник с вершинами в узлах и сторонами, идущими по линиям сетки (рис.8). Обозначим через В — количество узлов, лежащих внутри прямоугольника, а через Г – количество узлов на его границе. Сместим сетку на полклетки вправо и полклетки вниз. Тогда территорию прямоугольника можно «распределить» между узлами следующим образом: каждый из В узлов «контролирует» целую клетку смещённой сетки, а каждый из Г узлов – 4 граничных не угловых узла – половину клетки, а каждая из угловых точек – четверть клетки. Поэтому площадь прямоугольника вычисляется по формуле:

S = В + 4 · = В + – 1.

Итак, для прямоугольников с вершинами в узлах и сторонами, идущими по линиям сетки, освоили формулу S = В + – 1. Оказывается, эта формула верна не только для прямоугольников, но и для произвольных многоугольников с вершинами в узлах сетки! Это и есть формула Пика. [5]

Она секретной не является. Информация о ней в интернете имеется. Об этой формуле обычно рассказывается применительно к нахождению площади треугольника. На примере треугольника мы её и рассмотрим. Автор этой формулы австрийский математик Георг Пик (приложение 1). [2]

Можно убедиться в том, что формула Пика верна для всех рассмотренных выше примеров. Оказывается, что если многоугольник можно разрезать на треугольники с вершинами в узлах сетки, то для него верна формула Пика.

Рассмотрим применение формулы Пика на примерах:

Задача 7. Найдем площадь треугольника (см. рис.9). Отметим узлы (пересечение линий) на границе треугольника и внутри треугольника:

В = 34 (обозначены черным), Г = 15 (обозначены серым).

S= 34 + 15/2 – 1 = 40,5 ед² Ответ: 40,5

Понятно, что находить площадь трапеции, параллелограмма, треугольника проще и быстрее по соответствующим формулам площадей этих фигур. А вот когда дан многоугольник, у которого пять и более углов эта формула работает хорошо. [7]

Задача 8. Вычислим площадь пятиугольника (см.рис.10).

Отметим узлы (пересечение линий) на границе пятиугольника и внутри пятиугольника:

В = 43 (обозначены черным),

Г = 14 (обозначены серым).

S= 43 + 14/2 – 1 = 49 ед² Ответ: 49.

Конечно, есть ещё способы нахождения фигур на клеточной бумаге. Например, можно просто считать количество целых клеток внутри фигуры, а из оставшихся кусочков «складывать» целые клетки, но это довольно долго и трудно, особенно если фигура сложной формы.

Можно находить площади фигур на клеточной бумаге, используя формулы площади произвольного треугольника, трапеции, ромба, параллелограмма. Но для этого нужно знать эти формулы и уметь ими пользоваться.

И есть такие фигуры на клеточной бумаге, для которых эти формулы применить очень трудно, да и затратно по времени. А на экзамене по математике в 9-м и в 11-м классе каждая минута дорога!

2.4 Эксперимент и исследование

Мы решили провести эксперимент для того, чтобы выяснить какой из рассмотренных способов является самым эффективным, т.е. результативным (решение без ошибок) и малозатратным по времени.

Обучающимся 9-го и 11-го классов (13 и 8 человек соответственно) мы показали и объяснили способы нахождения площадей фигур на клетчатой бумаге. Ученики решали задачи с помощью способов описанных в п.2.1, 2.2 (приложение 2) [3], [6], [7]. Каждому нужно было решить по четыре задачи и засечь время их выполнения.

Затем рассказали им о формуле Пика, показали на примерах её применение и предложили решить другие задачи на клетчатой бумаге, но по формуле Пика (снова засекали время).

Результаты эксперимента представлены в таблицах (приложение 3).

Общие результаты эксперимента:

Затраченное время — среднее значение (мин)

Количество уч-ся, допустивших ошибки

Выполненный эксперимент показал, что:

Из двух классов почти никто не знал формулу Пика.
17 из 21 учащихся допустили ошибки при вычислении площадей фигур, используя одно из свойств площадей – площадь фигуры равна сумме площадей ее частей;
16 из 21 учащихся допустили ошибки при вычислении площадей фигур на клетчатой бумаге, используя правило площади фигуры, как части площади прямоугольника;
12 из 21 учащихся допустили ошибки при решении задач, используя формулу Пика;
количество ошибок, допущенных при решении задач по формуле Пика, сократилось;
количество безошибочных работ увеличилось;
время, затраченное на решение по формуле Пика, сократилось.

Существует достаточное количество способов нахождения площадей фигур на клетчатой бумаге. Мы рассмотрели основные из них. Задачи, поставленные в самом начале нашей работой, выполнили. Все способы нахождения площадей фигур на клетчатой бумаге хороши, но самым результативным оказался способ решения по формуле Пика!

Наша гипотеза подтвердилась. А тем выпускникам, которые недостаточно знают формулы площадей фигур или имеют проблемы с геометрией, эта работа – неоспоримая помощь в подготовке к выполнению таких заданий.

Список использованных источников и литературы

Виленкин В.Я. Математика 5 класс: учебник для учащихся общеобразовательных школ / В.Я. Виленкин. – М. : Мнемозина, 2016. – 280 с.
Смирнова И.М. Геометрия на клетчатой бумаге: учебно-методическое пособие / И.М. Смирнова, В.А. Смирнов – М: Чистые пруды, 2009. – 32 с.
Смирнова И.М. Геометрические задачи с практическим содержанием: пособие для учащихся / И.М. Смирнова, В.А. Смирнов – М.: Чистые пруды, 2010. – 136 с.
Википедия. Пик. Георг. [Электронный ресурс]. – Режим доступа: https://ru.wikipedia, свободный. – Загл. с экрана.
Жарковская Н.М., Рисс Е.А. Геометрия клетчатой бумаги. Формула Пика // Математика, 2009, № 17. – [Электронный ресурс]. – Режим доступа: http://mat.1september.ru/2009/23/gazeta_23_09.pdf, свободный. – Загл. с экрана.
ФИПИ. Открытый банк заданий ЕГЭ 2017-2018 по математике. – [Электронный ресурс]. – Режим доступа: http://www.fipi.ru/content/otkrytyy-bank-zadaniy-ege, свобоный. – Загл. с экрана.
Математика? Легко. Площади фигур. – [Электронный ресурс]. – Режим доступа: https://matematikalegko.ru/category/plocshadi-figur, свободный. – Загл. с экрана.
Фигуры на квадратной решётке — «РЕШУ ОГЭ»: математика. ОГЭ — [Электронный ресурс]. – Режим доступа: https://oge.sdamgia.ru/test?theme=14, свободный. Загл. с экрана.

Георг Алекса?ндр Пик (нем. Georg Alexander Pick; 10 августа 1859 г. – 13 июля 1942 г.) – австрийский математик. В 16 лет Георг окончил школу и поступил в Венский университет. В 20 лет получил право преподавать физику и математику. 16 апреля 1880 года под руководством Лео Кёнигсбергера Пик защитил докторскую диссертацию «О классе абелевых интегралов». В 1881 году он получил место ассистента у Эрнста Маха, который занял кафедру физики в Пражском университете. Чтобы получить право чтения лекций, Георгу необходимо было пройти хабилитацию. Для этого он написал работу «Об интеграции гиперэллиптических дифференциалов логарифмами». Это произошло в 1882 году, вскоре после разделения Пражского университета на чешский (Карлов университет) и немецкий (Университет Карла-Фердинанда). Пик остался в Немецком университете. В 1884 году Пик уехал в Лейпцигский университет к Феликсу Клейну. Там он познакомился с другим учеником Клейна, Давидом Гильбертом. Позже, в 1885 г., он вернулся в Прагу, где и прошла оставшаяся часть его научной карьеры. Преподавательская деятельность в Немецком университете в Праге в 1888 г. Пик получил место экстраординарного профессора математики, затем в 1892г. стал ординарным профессором. В 1910 г. Георг Пик был в комитете, созданном Немецким университетом Праги для рассмотрения вопроса о принятии Альберта Эйнштейна профессором в университет. Пик и физик Антон Лампа были главными инициаторами этого назначения, и благодаря их усилиям Эйнштейн, с которым Пик впоследствии сдружился, в 1911г. возглавил кафедру теоретической физики в Немецком университете в Праге. Круг математических интересов Пика был чрезвычайно широк. В частности, им написаны работы в области функционального анализа и дифферен-циальной геометрии, эллиптических и абелевых функций, теории дифференциальных уравнений и комплексного анализа, всего более 50 тем. С его именем связаны матрица Пика, интерполяция Пика — Неванлинны, лемма Шварца-Пика. Широкую известность получила открытая им в 1899 году теорема Пика для расчёта площади многоугольника. В Германии эта теорема включена в школьные учебники. [4]

Вычислить площадь фигуры, используя одно из свойств площадей – площадь фигуры равна сумме площадей ее частей.

Найдите площадь трапеции ABCD, считая стороны квадратных клеток равными 1.

Найдите площадь трапеции ABCD, считая стороны квадратных клеток равными 1.

Найдите площадь четырехугольника ABCD, считая стороны квадратных клеток равными 1.

Найдите площадь четырехугольника ABCD, считая стороны квадратных клеток равными 1.

Вычислить площадь фигуры, используя правило пощади фигуры как части площади прямоугольника.

Найдите площадь параллелограмма ABCD, считая стороны квадратных клеток равными 1.

Найдите площадь треугольника ABC, считая стороны квадратных клеток равными 1.

Найдите площадь трапеции ABCD, считая стороны квадратных клеток равными 1.

Найдите площадь четырехугольника ABCD, считая стороны квадратных клеток равными 1.

Вычислить площадь фигуры, используя формулу Пика.

Найдите площадь параллелограмма ABCD, считая стороны квадратных клеток равными 1.
Найдите площадь треугольника ABC, считая стороны квадратных клеток равными 1.
Найдите площадь трапеции ABCD, считая стороны квадратных клеток равными 1.
Найдите площадь четырехугольника ABCD, считая стороны квадратных клеток равными 1.