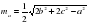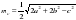Длина чевианы треугольника формула (5 видео)

Все формулы для треугольника

Содержание

1. Как найти неизвестную сторону треугольника
2. Как узнать сторону прямоугольного треугольника
3. Формулы сторон равнобедренного треугольника
4. Найти длину высоты треугольника
Чевианы треугольника
Просмотр содержимого документа «Чевианы треугольника»
Просмотр содержимого презентации «Чевианы треугольника»
Теорема Чевы: формулировка и пример с решением
Формулировка теоремы
Пример задачи
📽️ Видео

Видео:Длина медианы. Вывод формулыСкачать

1. Как найти неизвестную сторону треугольника

Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.

a , b , c — стороны произвольного треугольника

α , β , γ — противоположные углы

Формула длины через две стороны и угол (по теореме косинусов), ( a ):

* Внимательно , при подстановке в формулу, для тупого угла ( α >90), cos α принимает отрицательное значение

Формула длины через сторону и два угла (по теореме синусов), ( a):

Видео:Теорема Стюарта | формулы для биссектрисы треугольника и медианыСкачать

2. Как узнать сторону прямоугольного треугольника

Есть следующие формулы для определения катета или гипотенузы

a , b — катеты

c — гипотенуза

α , β — острые углы

Формулы для катета, ( a ):

Формулы для катета, ( b ):

Формулы для гипотенузы, ( c ):

Формулы сторон по теореме Пифагора, ( a , b ):

Видео:ЧевианаСкачать

3. Формулы сторон равнобедренного треугольника

Вычислить длину неизвестной стороны через любые стороны и углы

b — сторона (основание)

a — равные стороны

α — углы при основании

β — угол образованный равными сторонами

Формулы длины стороны (основания), (b ):

Формулы длины равных сторон , (a):

Видео:#189 ЧЕВИАНЫ // ТРЕУГОЛЬНИКСкачать

4. Найти длину высоты треугольника

Высота— перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).

Высоты треугольника пересекаются в одной точке, которая называется — ортоцентр.

H — высота треугольника

a — сторона, основание

b, c — стороны

β , γ — углы при основании

p — полупериметр, p=(a+b+c)/2

R — радиус описанной окружности

S — площадь треугольника

Формула длины высоты через стороны, ( H ):

Формула длины высоты через сторону и угол, ( H ):

Формула длины высоты через сторону и площадь, ( H ):

Формула длины высоты через стороны и радиус, ( H ):

Видео:Как найти длину биссектрисы, медианы и высоты? | Ботай со мной #031 | Борис ТрушинСкачать

Чевианы треугольника

Данная разработка — конспект факультативного занятия по теме «Чевианы треугольника» с презентацией. Цель занятия — систематизация знаний и введение дополнительных сведений о медианах, высотах и биссектрисах треугольника, применение полученных знаний для решения задач повышенной сложности, предлагаемых на ГИА и ЕГЭ.

Просмотр содержимого документа
«Чевианы треугольника»

Внеклассное мероприятие для учащихся 9-10 классов в рамках подготовки к ГИА и ЕГЭ

Софронова Н.А., учитель математики МОУ «Упшинская ООШ» Оршанского района РМЭ

Форма проведения – факультативное занятие

Обучающая: Систематизация знаний и введение дополнительных сведений о медианах, высотах и биссектрисах треугольника.

Развивающая: Применение полученных знаний для решения задач повышенной сложности.

Воспитательная: Формирование культуры умственного труда и интереса к предмету, установки на самообразование, коммуникабельности.

Презентация к уроку

Раздаточный материал: тексты задач, справочная информация

Комментарии к слайду

1. Организационный момент

Меня зовут Н.А. Я – учитель математики УООШ.

Сегодня, в рамках подготовки к ЕГЭ, мы поговорим о самой замечательной, на мой взгляд, геометрической фигуре – треугольнике.

Тема нашего занятия – ЧЕВИАНЫ ТРЕУГОЛЬНИКА. Я не буду объяснять вам значение слова ЧЕВИАНА. Я предполагаю, что к концу этого урока вы сами дадите ему толкование.

Эпиграф к уроку: «Три пути ведут к знанию: путь размышлений – самый благодарный, путь подражания – самый легкий и путь опыта – это путь самый горький.» (Конфуций)

Пусть этот час будет для вас дорогой размышления, приобретения нового опыта и использования старого с новых позиций.

Работа с презентацией.

2. Актуализация знаний

Итак – главный герой нашего занятия – треугольник. А что это такое? Перед вами несколько высказываний о треугольнике. Какое из них можно считать определением треугольника?

Треугольник – это фигура, состоящая из трех точек

Треугольник – это фигура, состоящая из трех отрезков

Треугольник – это фигура, состоящая из трех углов

Треугольник – это фигура, состоящая из трех точек и трех отрезков, соединяющих эти точки.

Работа с презентацией.

Каков правильный ответ?

На слайде нет верного определения треугольника.

Треугольник – это фигура, состоящая из трех точек, не лежащих на одной прямой, и трех отрезков, соединяющих эти точки.

Для понимания материала сегодняшнего занятия повторим метрические соотношения в треугольнике. А чтобы процесс повторения не был скучным, проведем его в виде игры «Банкиры».

В ходе игры участвуют две команды, каждая из которых представляет правление банка. Игроки выбирают президента банка. Президент от имени правления отвечает на предложенные в ходе игры задания различной стоимости (либо посоветовавшись с правлением, либо самостоятельно), тем самым увеличивая активы своего банка.

Банки – конкурирующие организации. У банков общая денежная единица — 1 «ум». У каждого банка – начальный стартовый капитал – 5 «умов».

Командам предлагаются по очереди задания различной стоимости. Если команда дает правильный ответ, то ее стартовый капитал увеличивается на стоимость задания. В противном случае – капитал уменьшается на стоимость задания, если на предложенный вопрос ответила другая команда и на половину стоимости задания, если на предложенный вопрос никто не ответил.

А сейчас проведем отборочный тур с целью выяснить, какая из команд начнет игру первой.

Работа с презентацией.

Раздать листочек со словами: ВД – это ….

Допустимы сокращения слова вплоть до одной буквы. Скорость и правильность .

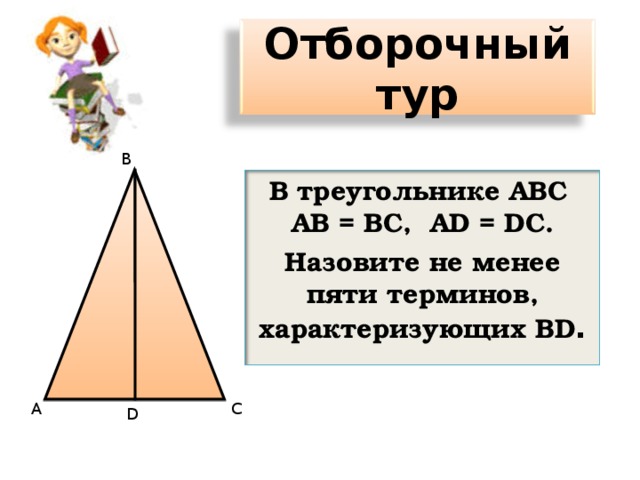
Задание отборочного тура

Напишите не менее пяти терминов, характеризующих В D .

Работа с презентацией.

P . S . Если количество ответов совпадает – жеребьевка (орел, решка)

высота, ось симметрии, ГМТ, равноудал. от А и С,

сер перпендикуляр к АС, чевиана, недиана,

Задание 1 стоимостью в 1 ум

Исключи лишнее слово в классификации треугольников

А. Остроугольные Б. Равнобедренные

В. Прямоугольные Г. Тупоугольные

Работа с презентацией.

Задание 2 стоимостью в 1 ум

Отрезок, соединяющий вершину треугольника с серединой противолежащей стороны —

А. высота Б. би ссектриса В. ср. линия Г. медиана

Работа с презентацией.

У вас есть возможность заработать еще по 1 «уму», если вы ответите на вопросы: что такое высота, медиана, биссектриса треугольн.

Б. – это отрезок биссектрисы угла тр-ка, соединяющий вершину с точкой противоположной стороны.

В. – перпендикуляр, проведенный из вершины к прямой, содерж, прот. стор.

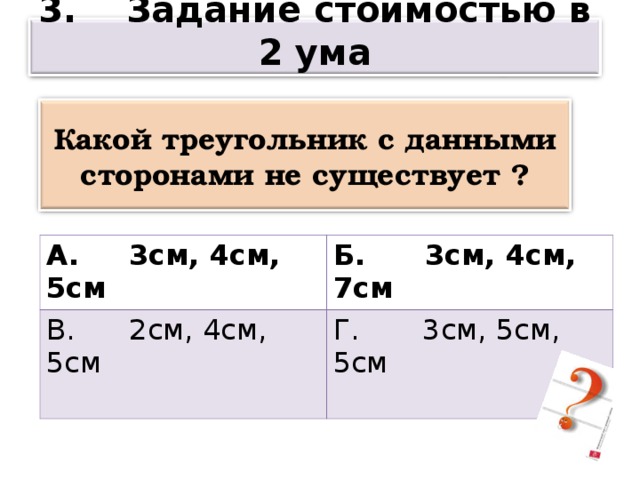
Задание 3 стоимостью в 2 ума

Какой треугольник с данными сторонами не существует ?

Работа с презентацией.

Напомнить неравенство треугольника

Задание 4 стоимостью в 2 ума

Какие числа соответствуют сторонам египетского треугольника?

А. 10, 15, 20 Б. 7, 8, 11

Работа с презентацией.

Уточнить, как по длинам сторон определить вид треугольника

Задание 5 стоимостью в 3 ума

Для треугольника АВС справедливо равенство:

Теорема косинусов для ВС

Работа с презентацией.

Дополнительный вопрос на 1 «ум» о нахождении углов по теореме косинусов.

Задание 6 стоимостью в 3 ума

По теореме синусов

А. стороны треугольника обр. пропор синусам противолеж углов

Б. стороны треугольника пропорцион синусам прилежащих углов

В. стороны треугольника пропорцион синусам противол. углов

Г. стороны треугольника обр. пропорц. синусам прилежащ углов

Работа с презенацией.

Задание 7 стоимостью в 3 ума

Какая из приведенных ниже формул не является формулой для нахождения площади треугольника?

Работа с презентацией.

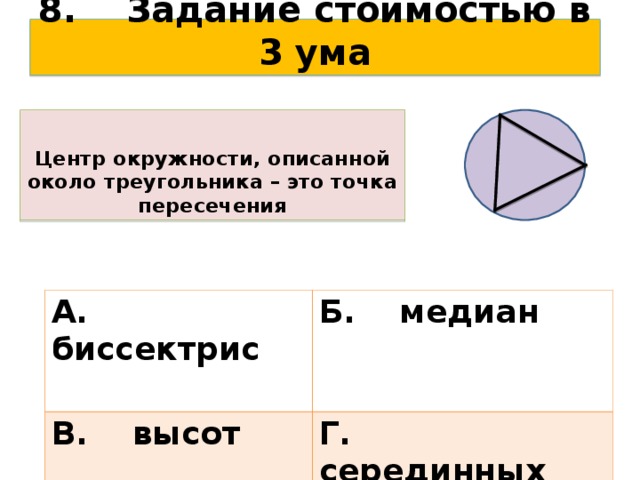
Задание 8 стоимостью в 3 ума

Центр окружности, описанной около треугольника – это точка пересечения

Г. серединных перпендикуляров

Работа с презентацией.

Уточнить: точка пересечения биссектрис – центр вписанной окр.

Дополнительные вопросы на 1 «ум»

Какими свойствами обладают медианы и биссектрисы треугольника?

Задание 9 стоимостью в 4 ума

Кто открыл формулу Герона?

«Метрика» ( Μετρική ) Герона — справочник по прикладной математике. Среди содержащихся в «Метрике» сведений: Формула Герона для расчёта площади треугольника по длинам его сторон, открытая Архимедом

Работа с презентацией.

Ответ: Б (Архимед)

Задание 10 стоимостью в 4 ума

Кто автор изречения: «Природа говорит языком математики, буквы этого языка – круги, треугольники и иные математические фигуры» ?

Работа с презентацией.

3. Постановка целей урока

Итак, в ходе игры мы повторили материал, относящийся к решению треугольников.

Однако при решении многих задач на «треугольник» этих знаний бывает недостаточно. Полезно взять на вооружение еще несколько формул на количественные соотношения в треугольнике, связанные с медианами, высотами и биссектрисами треугольника, а также формулы для вычисления их длин высот, медиан и биссектрис.

Раздать справочный материал по треугольнику

4.1. Свойства медианы треугольника

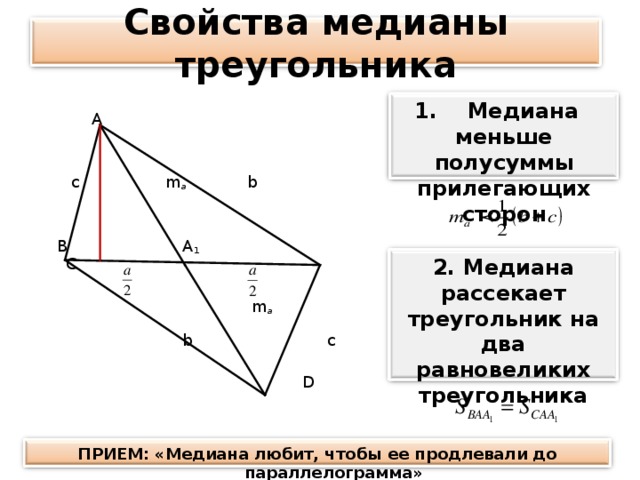
Свойства медианы треугольника

Медиана меньше полусуммы прилегающих сторон.

Медиана рассекает треугольник на два равновеликих треугольника

Работа с презентацией.

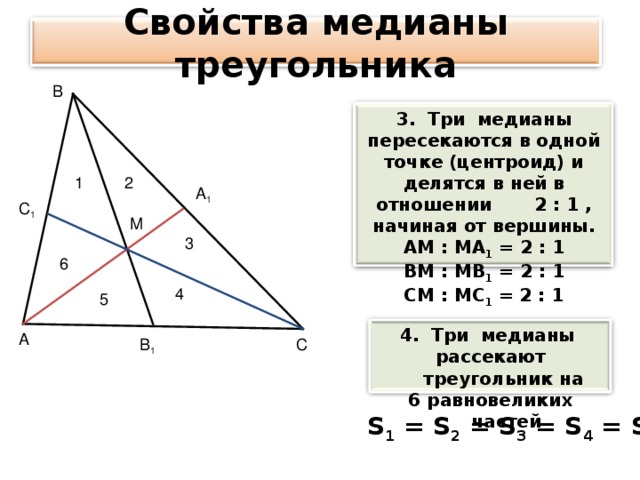
Три медианы пересекаются в одной точке и делятся в ней в отношении 2 : 1 , начиная от вершины.

Три медианы рассекают треугольник на

6 равновеликих частей

Работа с презентацией.

Задача: Медианы треугольника равны 9 см, 12 см и 15 см.

Найти отрезки, на которые они делятся точкой пересечения

2ч + 1 ч = 9 6 см и 3 см

2ч + 1 ч = 9 8 см и 4 см

2ч + 1 ч = 9 10 см и 5 см

Решение задач на свойства медианы

Дан треугольник АВ C со сторонами ВС = а, АС = b , АВ = c . Найти медиану, проведенную к стороне ВС

Работа с презентацией.

Совместный вывод формулы

У учеников РАЗДАТОЧНЫЙ МАТЕРИАЛ:

Записывают вывод формулы длины медианы

Дан треугольник АВ C со сторонами ВС = 9, АС = 7, АВ = 8. Найти медиану, проведенную к стороне АВ

АВ = с Найти m _c

Работа с презентацией.

Решают предложенные задачи: Задача 2.

АВ = с Найти m _c

Записывают формулу для m _c

Медианы треугольника равны 9, 12 и 15. Найдите площадь треугольника.

Основание треугольника равно 20 см, медианы боковых сторон равны 24 и 18 см. Найти площадь треугольника

Порекомендовать самостоятельно решить задачу 4 (д/з)

Реш.ение задачи 3.

Прием – до парал.ВАСД

Стороны тр. ВМД – 6,8 и 10 , он прямоугольн., Его площадь 24 см 2

Площадь тр. ВМА₁ — 12

Площадь тр.АВС — 72

Свойства биссектрисы треугольника

Биссектриса треугольника делит противоположную сторону на части, пропорциональные прилежащим к ней сторонам.

ВЕ – биссектриса. АЕ:ЕС = ВА : ВС

Найти отрезки, на которые биссектриса угла В треугольника АВС делит сторону АС, если а = 6,

Ответ: 4 см и 3 см

Работа с презентацией.

Вспоминаем еще раз свойства биссектрис треугольника

Три биссектрисы треугольника пересекаются в одной точке, называемой инцентром.

Точка пересечения биссектрис является центром вписанной в треугольник окружности.

ВЕ – биссектриса. АЕ:ЕС = ВА : ВС

Записывают реш. зад 5

Вывод формулы длины биссектрисы

Вывод формулы длины биссектрисы (план)

Работа с презентацией.

Составить формулы для двух других биссектрис

Работа с презентацией.

Вернуться к слайду 19

Проверить формулу для задачи 5

В треугольнике PQR длина биссектрисы РО равна 6, отношение длин отрезков QO и OR равно 3:4, периметр треугольника PQR равен 21. Чему равен косинус угла QPR ?

Работа с презентацией.

В треугольнике АВС длина стороны АВ равна 18, длина биссектрисы АЕ равна 4√15, а длина отрезка ЕС равна 5.

Определите периметр треугольника АВС.

предложить решить самостоятельно

Итоги соревнований банков

И еще мне хочется вернуться к словам великого Конфуция относительно дорог к знаниям и услышать от вас

Каков был ваш путь к знаниям на сегодняшнем занятии: подражания, опята или размышления?

Работа с презентацией.

Весь урок говорили о медианах, биссектрисах. К сожалению, время не позволило нам поговорить о высотах треугольника.

Почему же тема нашего мероприятия — ЧЕВИАНЫ ТРЕУГОЛЬНИКА?

Чевиана – это отрезок, соединяющий вершину и точку на противоположной стороне.

Просмотр содержимого презентации
«Чевианы треугольника»

Три пути ведут к знанию:

путь подражания – самый легкий

и путь опыта – это путь самый горький.

Треугольник – это фигура, состоящая из трех точек.
Треугольник – это фигура, состоящая из трех отрезков.
Треугольник – это фигура, состоящая из трех углов.
Треугольник – это фигура, состоящая из трех точек и трех отрезков, соединяющих эти точки.
Треугольник – это фигура, состоящая из трех точек,не лежащих на одной прямой, и трех отрезков, соединяющих эти точки.

В ходе игры участвуют две команды, каждая из которых представляет правление банка. Игроки выбирают президента банка. Президент от имени правления отвечает на предложенные в ходе игры задания (либо посоветовавшись с правлением, либо самостоятельно).
Банки – конкурирующие организации. У банков общая денежная единица — 1 «ум». У каждого банка – начальный стартовый капитал – 5 «умов».
Командам предлагаются по очереди задания различной стоимости. Если команда дает правильный ответ, то ее стартовый капитал увеличивается на стоимость задания . В противном случае – капитал уменьшается на стоимость задания, если на предложенный вопрос ответила другая команда и на половину стоимости задания, если на предложенный вопрос никто не ответил.

Назовите не менее пяти терминов, характеризующих В D .

1. Задание стоимостью в 1 ум

Исключи лишнее слово в классификации треугольников

2. Задание стоимостью в 1 ум

Отрезок, соединяющий вершину треугольника с серединой противолежащей стороны —

3. Задание стоимостью в 2 ума

Какой треугольник с данными сторонами не существует ?

4. Задание стоимостью в 2 ума

Какие числа соответствуют сторонам египетского треугольника?

5. Задание стоимостью в 3 ума

Для треугольника АВС справедливо равенство:

6. Задание стоимостью в 3 ума

По теореме синусов

А. стороны треугольника обратно пропорциональны синусам противолежащих углов

Б. стороны треугольника пропорциональны синусам прилежащих углов

В. стороны треугольника пропорциональны синусам противолежащих углов

Г. стороны треугольника обратно пропорциональны синусам прилежащих углов

7. Задание стоимостью в 3 ума

Какая из приведенных ниже формул не является формулой для нахождения площади треугольника?

8. Задание стоимостью в 3 ума

Центр окружности, описанной около треугольника – это точка пересечения

Г. серединных перпендикуляров

9. Задание стоимостью в 4 ума

Кто открыл формулу Герона?

8. Задание стоимостью в 3 ума

10. Задание стоимостью в 4 ума

Свойства медианы треугольника

меньше полусуммы прилегающих сторон

2. Медиана рассекает треугольник на два равновеликих треугольника

ПРИЕМ: «Медиана любит, чтобы ее продлевали до параллелограмма»

Свойства медианы треугольника

3. Три медианы пересекаются в одной точке (центроид) и делятся в ней в отношении 2 : 1 , начиная от вершины.

Видео:✓ Новая формула площади треугольника | Ботай со мной #108 | Борис ТрушинСкачать

Теорема Чевы: формулировка и пример с решением

В данной публикации мы рассмотрим одну из классических теорем аффинной геометрии – теорему Чевы, которая получила такое название в честь итальянского инженера Джованни Чевы. Также разберем пример решения задачи, чтобы закрепить представленный материал.

Видео:9 класс. Геометрия. Теорема Чевы.Скачать

Формулировка теоремы

Дан треугольник ABC, в котором каждая вершина соединена с точкой на противоположной стороне.

Таким образом, мы получаем три отрезка (AA’, BB’ и CC’), которые называются чевианами.

Данные отрезки пересекаются в одной точке тогда и только тогда, когда выполняется следующее равенство:

Теорему можно, также, представить в таком виде (определяется, в каком соотношении точки делят стороны):

Тригонометрическая теорема Чевы

Примечание: все углы – ориентированные.

Видео:Математика-954. Чевиана и площади.Скачать

Пример задачи

Дан треугольник ABC с точками A’, B’ и C’ на сторонах BC, AC и AB, соответственно. Вершины треугольника соединены с данным точками, и образованные отрезки проходят через одну точку. При этом точки A’ и B’ взяты на серединах соответствующих противоположных сторон. Выясните, в каком соотношении точка C’ делит сторону AB.

Решение
Нарисуем чертеж согласно условиям задачи. Для нашего удобства примем следующие обозначения:

Остается только составить соотношение отрезков согласно теореме Чевы и подставить в него принятые обозначения:

После сокращения дробей получаем:

Значит, AC’ = C’B, т.е. точка C’ делит сторону AB пополам.

Следовательно, в нашем треугольнике отрезки AA’, BB’ и CC’ являются медианами. Решив задачу мы доказали, что они пересекаются в одной точке (справедливо для любого треугольника).

Примечание: с помощью теоремы Чевы можно доказать, что в треугольнике в одной точке, также, пересекаются биссектрисы или высоты.