- Найдите координаты точек числовой окружности : 45П / 4 = 45 / 4 * П = (10 + 5 / 4) * П — 37П / 3 = — 37 / 3 * П = (12 + 1 / 3) * П Не понятно действие в скобках, откуда взялось 10 и 5 / 4?
- Центр окружности А(4?
- (ТРИГОНОМЕТРИЯ) Объяснить действия в примере?
- Не выполняя построений, найдите координаты точек пересечения параболы у = х² — 5 и окружности х² + у² = 25?
- Не выполняя построений, найдите координаты точек пересечения окружности Х в квадрате + у в квадрате = 86 3х + у = 10 и все это в большой скобке?
- Решите эти уравнение ?
- Найдите координаты точек пересечения прямой у = 3 + х и окружности х2 + у2 = 9?
- Как определить координаты точки на числовой окружности, под углом 60 °?
- Не выполняя построение, найдите координаты точек пересечения окружности х² + у² = 10 и прямой х + 2у = 5?
- Откуда взялся корень из 2 в третье строчки?
- Как связаны между собой абсциссы точек числовой окружности : а)t и — t б) t и t + П Как связаны между собой ординаты точек числовой окружности а) t и — t б)t и t + П?
- Единичная числовая окружность на координатной плоскости
- п.1. Понятие тригонометрии
- п.2. Числовая окружность
- п.3. Градусная и радианная мера угла
- п.4. Свойства точки на числовой окружности
- п.5. Интервалы и отрезки на числовой окружности
- п.6. Примеры
- Найти координаты точек числовой окружности 45п
- Найти координаты точек числовой окружности 45п
- Как написать хороший ответ?
- Единичная числовая окружность на координатной плоскости
- п.1. Понятие тригонометрии
- п.2. Числовая окружность
- п.3. Градусная и радианная мера угла
- п.4. Свойства точки на числовой окружности
- п.5. Интервалы и отрезки на числовой окружности
- п.6. Примеры
- Числовая окружность
- Длина числовой окружности равна (2π) или примерно (6,28).
- Какие точки соответствуют числам (1), (2) и т.д?
- Чтобы отметить на числовой окружности точку соответствующую числу 1, нужно от 0 пройти расстояние равное радиусу в положительном направлении.
- Главное свойство числовой окружности
- Одному числу на числовой окружности соответствует одна точка, но одной точке соответствует множество чисел.
- Все значения одной точки на числовой окружности можно записать с помощью формулы:
- 🎥 Видео
Видео:Координаты точек на числовой окружности, часть 5. Алгебра 10 класс.Скачать
Найдите координаты точек числовой окружности : 45П / 4 = 45 / 4 * П = (10 + 5 / 4) * П — 37П / 3 = — 37 / 3 * П = (12 + 1 / 3) * П Не понятно действие в скобках, откуда взялось 10 и 5 / 4?
Алгебра | 10 — 11 классы
Найдите координаты точек числовой окружности : 45П / 4 = 45 / 4 * П = (10 + 5 / 4) * П — 37П / 3 = — 37 / 3 * П = (12 + 1 / 3) * П Не понятно действие в скобках, откуда взялось 10 и 5 / 4?
Аналогично и со вторым, объясните.
45П / 4 = 45 / 4 * П = (10 + 5 / 4) * П = 5 / 4 * π = π + π / 4 3 четверть,
координаты ( — √2 / 2 ; — √2 / 2)
45 / 4 = 10 5 / 4 = 10 + 5 / 4 — 37П / 3 = — 37 / 3 * П = — (12 + 1 / 3) * П = — π / 3 4 четверть,
координата х определяется по косинусу угла, а координата у по синусу угла.
Видео:10 класс, 11 урок, Числовая окружностьСкачать
Центр окружности А(4?
Центр окружности А(4.
Найдите координаты точек пересечения этой окружности с координатными осями.
Видео:Координаты точек на числовой окружности. Алгебра 10 класс.Скачать
(ТРИГОНОМЕТРИЯ) Объяснить действия в примере?
(ТРИГОНОМЕТРИЯ) Объяснить действия в примере.
Обратить особое внимание на выделенный красным момент.
Куда пропали и откуда взялись цифры?
Видео:Как найти координаты точек на тригонометрической окружностиСкачать
Не выполняя построений, найдите координаты точек пересечения параболы у = х² — 5 и окружности х² + у² = 25?
Не выполняя построений, найдите координаты точек пересечения параболы у = х² — 5 и окружности х² + у² = 25.
Видео:Координаты точек на числовой окружности, часть 2. Алгебра 10 класс.Скачать
Не выполняя построений, найдите координаты точек пересечения окружности Х в квадрате + у в квадрате = 86 3х + у = 10 и все это в большой скобке?
Не выполняя построений, найдите координаты точек пересечения окружности Х в квадрате + у в квадрате = 86 3х + у = 10 и все это в большой скобке.
Видео:Точки на числовой окружностиСкачать
Решите эти уравнение ?
Решите эти уравнение .
Что откуда взялось обьяснить.
Видео:Координаты точек на числовой окружности, часть 3. Алгебра 10 класс.Скачать
Найдите координаты точек пересечения прямой у = 3 + х и окружности х2 + у2 = 9?
Найдите координаты точек пересечения прямой у = 3 + х и окружности х2 + у2 = 9.
Видео:Как искать точки на тригонометрической окружности.Скачать
Как определить координаты точки на числовой окружности, под углом 60 °?
Как определить координаты точки на числовой окружности, под углом 60 °.
Видео:10 класс, 12 урок, Числовая окружность на координатной плоскостиСкачать
Не выполняя построение, найдите координаты точек пересечения окружности х² + у² = 10 и прямой х + 2у = 5?
Не выполняя построение, найдите координаты точек пересечения окружности х² + у² = 10 и прямой х + 2у = 5.
Видео:§22 Поворот точки вокруг начала координатСкачать
Откуда взялся корень из 2 в третье строчки?
Откуда взялся корень из 2 в третье строчки?
Видео:Алгебра. Декартовы координаты точек числовой окружности. (10 класс)Скачать
Как связаны между собой абсциссы точек числовой окружности : а)t и — t б) t и t + П Как связаны между собой ординаты точек числовой окружности а) t и — t б)t и t + П?
Как связаны между собой абсциссы точек числовой окружности : а)t и — t б) t и t + П Как связаны между собой ординаты точек числовой окружности а) t и — t б)t и t + П.
Перед вами страница с вопросом Найдите координаты точек числовой окружности : 45П / 4 = 45 / 4 * П = (10 + 5 / 4) * П — 37П / 3 = — 37 / 3 * П = (12 + 1 / 3) * П Не понятно действие в скобках, откуда взялось 10 и 5 / 4?, который относится к категории Алгебра. Уровень сложности соответствует учебной программе для учащихся 10 — 11 классов. Здесь вы найдете не только правильный ответ, но и сможете ознакомиться с вариантами пользователей, а также обсудить тему и выбрать подходящую версию. Если среди найденных ответов не окажется варианта, полностью раскрывающего тему, воспользуйтесь «умным поиском», который откроет все похожие ответы, или создайте собственный вопрос, нажав кнопку в верхней части страницы.
Видео:Координаты точек на числовой окружности, часть 4, супер важная часть. Алгебра 10 класс.Скачать
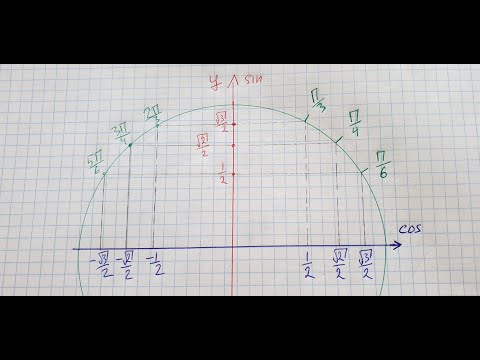
Единичная числовая окружность на координатной плоскости
п.1. Понятие тригонометрии
Тригонометрия берёт своё начало в Древней Греции. Само слово «тригонометрия» по-гречески означает «измерение треугольников». Эта наука в течение тысячелетий используется землемерами, архитекторами и астрономами.
Начиная с Нового времени, тригонометрия заняла прочное место в физике, в частности, при описании периодических процессов. Например, переменный ток в розетке генерируется в периодическом процессе. Поэтому любой электрический или электронный прибор у вас в доме: компьютер, смартфон, микроволновка и т.п., — спроектирован с использованием тригонометрии.
Базовым объектом изучения в тригонометрии является угол.
Предметом изучения тригонометрии как раздела математики выступают:
1) взаимосвязи между углами и сторонами треугольника, которые называют тригонометрическими функциями;
2) использование тригонометрических функций в геометрии.
п.2. Числовая окружность
Мы уже знакомы с числовой прямой (см. §16 справочника для 8 класса) и координатной плоскостью (см. §35 справочника для 7 класса), с помощью которых создаются графические представления числовых промежутков и функций. Это удобный инструмент моделирования, с помощью которого можно провести анализ, начертить график, найти область допустимых значений и решить задачу.
Для работы с углами и их функциями существует аналогичный инструмент – числовая окружность.
 | Числовая окружность (тригонометрический круг) – это окружность единичного радиуса R=1 с центром в начале координат (0;0). Точка с координатами (1;0) является началом отсчета , ей соответствует угол, равный 0. Углы на числовой окружности отсчитываются против часовой стрелки. Направление движения против часовой стрелки является положительным ; по часовой стрелке – отрицательным . |
| Отметим на числовой окружности углы 30°, 45°, 90°, 120°, 180°, а также –30°, –45°, –90°, –120°, –180°. |  |
п.3. Градусная и радианная мера угла
Углы можно измерять в градусах или в радианах.
Известно, что развернутый угол, дуга которого равна половине окружности, равен 180°. Прямой угол, дуга которого равна четверти окружности, равен 90°. Тогда полная, замкнутая дуга окружности составляет 360°.
Приписывание развернутому углу меры в 180°, а прямому 90°, достаточно произвольно и уходит корнями в далёкое прошлое. С таким же успехом это могло быть 100° и 50°, или 200° и 100° (что, кстати, предлагалось одним из декретов во времена французской революции 1789 г.).
В целом, более обоснованной и естественной для измерения углов является радианная мера.
 | Найдем радианную меру прямого угла ∠AOB=90°. Построим окружность произвольного радиуса r с центром в вершине угла – точке O. Длина этой окружности: L=2πr. Длина дуги AB: (l_=frac=frac=frac.) Тогда радианная мера угла: $$ angle AOB=frac<l_>=frac=frac $$ |
| 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° | 270° | 360° |
| (frac) | (frac) | (frac) | (frac) | (frac) | (frac) | (frac) | (pi) | (frac) | (2pi) |
п.4. Свойства точки на числовой окружности
Построим числовую окружность. Обозначим O(0;0), A(1;0)
 | Каждому действительному числу t на числовой окружности соответствует точка Μ(t). При t=0, M(0)=A. При t>0 двигаемся по окружности против часовой стрелки, описывая дугу ⌒ AM=t. Точка M — искомая. При t Например: |
| Отметим на числовой окружности точки, соответствующие (frac, frac, frac, frac, pi), а также (-frac, -frac, -frac, -frac, -pi) Для этого нужно отложить углы 30°, 45°, 90°, 120°, 180° и –30°, –45°, –90°, –120°, –180° с вершиной в начале координат и отметить соответствующие дуги на числовой окружности. |  |
| Отметим на числовой окружности точки, соответствующие (frac, frac, frac), и (-frac). Все четыре точки совпадают, т.к. begin Mleft(fracright)=Mleft(frac+2pi kright)\ frac-2pi=-frac\ frac+2pi=frac\ frac+4pi=frac end |  |
п.5. Интервалы и отрезки на числовой окружности
Каждому действительному числу соответствует точка на числовой окружности. Соответственно, числовые промежутки (см. §16 справочника для 8 класса) получают свои отображения в виде дуг.
| Числовой промежуток | Соответствующая дуга числовой окружности |
| Отрезок | |
$$ -frac lt t lt frac $$  а также, с учетом периода $$ -frac+2pi klt tltfrac+2pi k $$ |  |
| Интервал | |
$$ -frac leq t leq frac $$  а также, с учетом периода $$ -frac+2pi kleq tleqfrac+2pi k $$ |  |
| Полуинтервал | |
$$ -frac leq t ltfrac $$  а также, с учетом периода $$ -frac+2pi kleq tltfrac+2pi k $$ |  |
п.6. Примеры
Пример 1. Точка E делит числовую окружность во второй четверти в отношении 1:2.
Чему равны дуги AE, BE, EC, ED в градусах и радианах?
Угловая мера четверти 90°. При делении в отношении 1:2 получаем дуги 30° и 60° соответственно: begin BE=30^=frac.\ EC=60^=frac.\ AE=EC+CD=90^+30^=120^=frac.\ ED=EC+CD=60^+90^=150^=frac. end
Пример 2. Найдите на числовой окружности точку, соответствующую данному числу: (-frac; frac; frac; frac).
| Находим соответствующие углы в градусах и откладываем с помощью транспортира (положительные – против часовой стрелки, отрицательные – по часовой стрелке), отмечаем соответствующие точки на числовой окружности. begin -frac=-90^, frac=135^\ frac=210^, frac=315^ end |  |
Пример 3. Найдите на числовой окружности точку, соответствующую данному числу: (-frac; 5pi; frac; frac).
| Выделяем из дроби целую часть, отнимаем/прибавляем один или больше полных оборотов (2πk — четное количество π), чтобы попасть в промежуток от 0 до 2π. Далее – действуем, как в примере 2. begin -frac=fraccdotpi=-6pi+fracrightarrow frac=90^\ 5pi=4pi+pirightarrow pi=180^\ frac=fracpi=3pi-fracrightarrow pi-frac=frac\ frac=fracpi=7pi-fracrightarrow pi-frac=frac end |  |
Пример 4. В какой четверти числовой окружности находится точка, соответствующая числу: 2; 4; 5; 7.
 | Сравниваем каждое число с границами четвертей: begin 0, fracpi2approxfrac=1,57, piapprox 3,14\ 3pi 3cdot 3,14\ fracapprox frac=4,71, 2piapprox 6,28 end |
(fracpi2lt 2lt pi Rightarrow ) угол 2 радиана находится во 2-й четверти
(pilt 4lt frac Rightarrow ) угол 4 радиана находится в 3-й четверти
(fraclt 5lt 2pi Rightarrow ) угол 5 радиана находится в 4-й четверти
(7gt 2pi), отнимаем полный оборот: (0lt 7-2pilt fracpi2Rightarrow) угол 7 радиан находится в 1-й четверти.
Пример 5. Изобразите на числовой окружности множество точек ((kinmathbb)), запишите количество полученных базовых точек.
| $$ frac $$ | $$ -frac+2pi k $$ |
 Четыре базовых точки, через каждые 90° |  Две базовых точки, через каждые 180° |
| $$ frac+frac $$ | $$ -frac $$ |
 Три базовых точки, через каждые 120° |  Пять базовых точек, через каждые 72° |
Пример 6. Изобразите на числовой окружности дуги, соответствующие числовым промежуткам.
Видео:Тригонометрическая окружность. Как выучить?Скачать
Найти координаты точек числовой окружности 45п
Видео:Найти координаты точки единичной окружности полученной при повороте точки Ро(1;0) на угол π, 450°...Скачать
Найти координаты точек числовой окружности 45п
Вопрос по алгебре:
Найдите координаты точек числовой окружности:
45П/4= 45/4* П= (10+5/4)*П
-37П/3= -37/3* П= (12+1/3)* П
Не понятно действие в скобках, откуда взялось 10 и 5/4? Аналогично и со вторым, объясните.
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!
Ответы и объяснения 1
45П/4= 45/4* П= (10+5/4)*П=5/4*π=π+π/4 3 четверть,
координаты (-√2/2;-√2/2)
45/4=10 5/4=10+5/4
-37П/3= -37/3* П=- (12+1/3)* П=-π/3 4 четверть,
координаты (1/2;-√3/2)
————————————————-
координата х определяется по косинусу угла,а координата у по синусу угла
Знаете ответ? Поделитесь им!
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
- Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
- Писать без грамматических, орфографических и пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
- Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
- Использовать мат — это неуважительно по отношению к пользователям;
- Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Алгебра.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!
Алгебра — раздел математики, который можно нестрого охарактеризовать как обобщение и расширение арифметики.
Видео:Косинус на числовой окружности. Алгебра 10 класс.Скачать
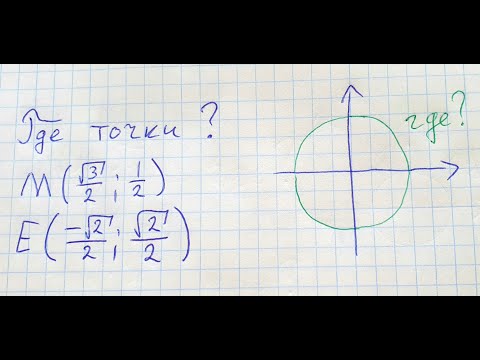
Единичная числовая окружность на координатной плоскости
п.1. Понятие тригонометрии
Тригонометрия берёт своё начало в Древней Греции. Само слово «тригонометрия» по-гречески означает «измерение треугольников». Эта наука в течение тысячелетий используется землемерами, архитекторами и астрономами.
Начиная с Нового времени, тригонометрия заняла прочное место в физике, в частности, при описании периодических процессов. Например, переменный ток в розетке генерируется в периодическом процессе. Поэтому любой электрический или электронный прибор у вас в доме: компьютер, смартфон, микроволновка и т.п., — спроектирован с использованием тригонометрии.
Базовым объектом изучения в тригонометрии является угол.
Предметом изучения тригонометрии как раздела математики выступают:
1) взаимосвязи между углами и сторонами треугольника, которые называют тригонометрическими функциями;
2) использование тригонометрических функций в геометрии.
п.2. Числовая окружность
Мы уже знакомы с числовой прямой (см. §16 справочника для 8 класса) и координатной плоскостью (см. §35 справочника для 7 класса), с помощью которых создаются графические представления числовых промежутков и функций. Это удобный инструмент моделирования, с помощью которого можно провести анализ, начертить график, найти область допустимых значений и решить задачу.
Для работы с углами и их функциями существует аналогичный инструмент – числовая окружность.
| Числовая окружность (тригонометрический круг) – это окружность единичного радиуса R=1 с центром в начале координат (0;0). Точка с координатами (1;0) является началом отсчета , ей соответствует угол, равный 0. Углы на числовой окружности отсчитываются против часовой стрелки. Направление движения против часовой стрелки является положительным ; по часовой стрелке – отрицательным . |
| Отметим на числовой окружности углы 30°, 45°, 90°, 120°, 180°, а также –30°, –45°, –90°, –120°, –180°. | |
п.3. Градусная и радианная мера угла
Углы можно измерять в градусах или в радианах.
Известно, что развернутый угол, дуга которого равна половине окружности, равен 180°. Прямой угол, дуга которого равна четверти окружности, равен 90°. Тогда полная, замкнутая дуга окружности составляет 360°.
Приписывание развернутому углу меры в 180°, а прямому 90°, достаточно произвольно и уходит корнями в далёкое прошлое. С таким же успехом это могло быть 100° и 50°, или 200° и 100° (что, кстати, предлагалось одним из декретов во времена французской революции 1789 г.).
В целом, более обоснованной и естественной для измерения углов является радианная мера.
| Найдем радианную меру прямого угла ∠AOB=90°. Построим окружность произвольного радиуса r с центром в вершине угла – точке O. Длина этой окружности: L=2πr. Длина дуги AB: (l_=frac =frac =frac .) Тогда радианная мера угла: $$ angle AOB=frac =frac =frac $$ |
| 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° | 270° | 360° |
| (frac ) | (frac ) | (frac ) | (frac ) | (frac ) | (frac ) | (frac ) | (pi) | (frac ) | (2pi) |
п.4. Свойства точки на числовой окружности
Построим числовую окружность. Обозначим O(0;0), A(1;0)
| Каждому действительному числу t на числовой окружности соответствует точка Μ(t). При t=0, M(0)=A. При t>0 двигаемся по окружности против часовой стрелки, описывая дугу ⌒ AM=t. Точка M — искомая. При t Например: |
| Отметим на числовой окружности точки, соответствующие (frac , frac , frac , frac , pi), а также (-frac , -frac , -frac , -frac , -pi) Для этого нужно отложить углы 30°, 45°, 90°, 120°, 180° и –30°, –45°, –90°, –120°, –180° с вершиной в начале координат и отметить соответствующие дуги на числовой окружности. | |
| Отметим на числовой окружности точки, соответствующие (frac , frac , frac ), и (-frac ). Все четыре точки совпадают, т.к. begin Mleft(frac right)=Mleft(frac +2pi kright)\ frac -2pi=-frac \ frac +2pi=frac \ frac +4pi=frac end | |
п.5. Интервалы и отрезки на числовой окружности
Каждому действительному числу соответствует точка на числовой окружности. Соответственно, числовые промежутки (см. §16 справочника для 8 класса) получают свои отображения в виде дуг.
| Числовой промежуток | Соответствующая дуга числовой окружности |
| Отрезок | |
| $$ -frac lt t lt frac $$ а также, с учетом периода $$ -frac +2pi klt tltfrac +2pi k $$ | |
| Интервал | |
| $$ -frac leq t leq frac $$ а также, с учетом периода $$ -frac +2pi kleq tleqfrac +2pi k $$ | |
| Полуинтервал | |
| $$ -frac leq t ltfrac $$ а также, с учетом периода $$ -frac +2pi kleq tltfrac +2pi k $$ | |
п.6. Примеры
Пример 1. Точка E делит числовую окружность во второй четверти в отношении 1:2.
Чему равны дуги AE, BE, EC, ED в градусах и радианах?
Угловая мера четверти 90°. При делении в отношении 1:2 получаем дуги 30° и 60° соответственно: begin BE=30^ =frac .\ EC=60^ =frac .\ AE=EC+CD=90^ +30^ =120^ =frac .\ ED=EC+CD=60^ +90^ =150^ =frac . end
Пример 2. Найдите на числовой окружности точку, соответствующую данному числу: (-frac ; frac ; frac ; frac ).
| Находим соответствующие углы в градусах и откладываем с помощью транспортира (положительные – против часовой стрелки, отрицательные – по часовой стрелке), отмечаем соответствующие точки на числовой окружности. begin -frac =-90^ , frac =135^ \ frac =210^ , frac =315^ end | |
Пример 3. Найдите на числовой окружности точку, соответствующую данному числу: (-frac ; 5pi; frac ; frac ).
| Выделяем из дроби целую часть, отнимаем/прибавляем один или больше полных оборотов (2πk — четное количество π), чтобы попасть в промежуток от 0 до 2π. Далее – действуем, как в примере 2. begin -frac =frac cdotpi=-6pi+frac rightarrow frac =90^ \ 5pi=4pi+pirightarrow pi=180^ \ frac =frac pi=3pi-frac rightarrow pi-frac =frac \ frac =frac pi=7pi-frac rightarrow pi-frac =frac end | |
Пример 4. В какой четверти числовой окружности находится точка, соответствующая числу: 2; 4; 5; 7.
| Сравниваем каждое число с границами четвертей: begin 0, fracpi2approxfrac =1,57, piapprox 3,14\ 3pi 3cdot 3,14\ frac approx frac =4,71, 2piapprox 6,28 end |
(fracpi2lt 2lt pi Rightarrow ) угол 2 радиана находится во 2-й четверти
(pilt 4lt frac Rightarrow ) угол 4 радиана находится в 3-й четверти
(frac lt 5lt 2pi Rightarrow ) угол 5 радиана находится в 4-й четверти
(7gt 2pi), отнимаем полный оборот: (0lt 7-2pilt fracpi2Rightarrow) угол 7 радиан находится в 1-й четверти.
Пример 5. Изобразите на числовой окружности множество точек ((kinmathbb )), запишите количество полученных базовых точек.
| $$ frac $$ | $$ -frac +2pi k $$ |
Четыре базовых точки, через каждые 90° | Две базовых точки, через каждые 180° |
| $$ frac +frac $$ | $$ -frac $$ |
Три базовых точки, через каждые 120° | Пять базовых точек, через каждые 72° |
Пример 6. Изобразите на числовой окружности дуги, соответствующие числовым промежуткам.
Видео:45 Где лежат на единичной окружности точки π/4, 3π/4Скачать
Числовая окружность
В этой статье мы очень подробно разберем определение числовой окружности, узнаем её главное свойство и расставим числа 1,2,3 и т.д. Про то, как отмечать другие числа на окружности (например, (frac , frac , frac , 10π, -frac )) разбирается в этой статье .
Числовой окружностью называют окружность единичного радиуса, точки которой соответствуют действительным числам , расставленным по следующим правилам:
1) Начало отсчета находится в крайней правой точке окружности;
2) Против часовой стрелки — положительное направление; по часовой – отрицательное;
3) Если в положительном направлении отложить на окружности расстояние (t), то мы попадем в точку со значением (t);
4) Если в отрицательном направлении отложить на окружности расстояние (t), то мы попадем в точку со значением (–t).
Почему окружность называется числовой?
Потому что на ней обозначаются числа. В этом окружность похожа на числовую ось – на окружности, как и на оси, для каждого числа есть определенная точка.
Зачем знать, что такое числовая окружность?
С помощью числовой окружности определяют значение синусов, косинусов, тангенсов и котангенсов. Поэтому для знания тригонометрии и сдачи ЕГЭ на 60+ баллов, обязательно нужно понимать, что такое числовая окружность и как на ней расставить точки.
Что в определении означают слова «…единичного радиуса…»?
Это значит, что радиус этой окружности равен (1). И если мы построим такую окружность с центром в начале координат, то она будет пересекаться с осями в точках (1) и (-1).
Ее не обязательно рисовать маленькой, можно изменить «размер» делений по осям, тогда картинка будет крупнее (см. ниже).
Почему радиус именно единица? Так удобнее, ведь в этом случае при вычислении длины окружности с помощью формулы (l=2πR) мы получим:
Длина числовой окружности равна (2π) или примерно (6,28).
А что значит «…точки которой соответствуют действительным числам»?
Как говорили выше, на числовой окружности для любого действительного числа обязательно найдется его «место» — точка, которая соответствует этому числу.
Зачем определять на числовой окружности начало отсчета и направления?
Главная цель числовой окружности — каждому числу однозначно определить свою точку. Но как можно определить, где поставить точку, если неизвестно откуда считать и куда двигаться?
Тут важно не путать начало отсчета на координатной прямой и на числовой окружности – это две разные системы отсчета! А так же не путайте (1) на оси (x) и (0) на окружности – это точки на разных объектах.
Видео:Координаты точек на числовой окружности, часть 6. Алгебра 10 класс.Скачать
Какие точки соответствуют числам (1), (2) и т.д?
Помните, мы приняли, что у числовой окружности радиус равен (1)? Это и будет нашим единичным отрезком (по аналогии с числовой осью), который мы будем откладывать на окружности.
Чтобы отметить на числовой окружности точку соответствующую числу 1, нужно от 0 пройти расстояние равное радиусу в положительном направлении.
Чтобы отметить на окружности точку соответствующую числу (2), нужно пройти расстояние равное двум радиусам от начала отсчета, чтобы (3) – расстояние равное трем радиусам и т.д.
При взгляде на эту картинку у вас могут возникнуть 2 вопроса:
1. Что будет, когда окружность «закончится» (т.е. мы сделаем полный оборот)?
Ответ: пойдем на второй круг! А когда и второй закончится, пойдем на третий и так далее. Поэтому на окружность можно нанести бесконечное количество чисел.
2. Где будут отрицательные числа?
Ответ: там же! Их можно так же расставить, отсчитывая от нуля нужное количество радиусов, но теперь в отрицательном направлении.
К сожалению, обозначать на числовой окружности целые числа затруднительно. Это связано с тем, что длина числовой окружности будет равна не целому числу: (2π). И на самых удобных местах (в точках пересечения с осями) тоже будут не целые числа, а доли числа (π) : ( frac ),(-frac ),(frac ), (2π). Поэтому при работе с окружностью чаще используют числа с (π). Обозначать такие числа гораздо проще (как это делается можете прочитать в этой статье ).
Видео:№976. Найдите координаты точки пересечения прямых 4x + 3y-6 = 0 и 2х+у-4 = 0.Скачать
Главное свойство числовой окружности
Одному числу на числовой окружности соответствует одна точка, но одной точке соответствует множество чисел.
Такая вот математическая полигамия.
И следствие из этого правила:
Все значения одной точки на числовой окружности можно записать с помощью формулы:
Если хотите узнать логику этой формулы, и зачем она нужна, посмотрите это видео .
В данной статье мы рассмотрели только теорию о числовой окружности, о том как расставляются точки на числовой и окружности и принципе, как с ней работать вы можете прочитать здесь .
Что надо запомнить про числовую окружность:
🎥 Видео
Соответствие чисел точкам числовой окружностиСкачать
ЧТО НАДО ГОВОРИТЬ ЕСЛИ НЕ СДЕЛАЛ ДОМАШКУ!Скачать
