Как найти нормальный вектор по трем точкам (5 видео)

Нормальный вектор плоскости, координаты нормального вектора плоскости

Существует ряд заданий, которым для решения необходимо нормальный вектор на плоскости, чем саму плоскость. Поэтому в этой статье получим ответ на вопрос определения нормального вектора с примерами и наглядными рисунками. Определим векторы трехмерного пространства и плоскости по уравнениям.

Содержание

Нормальный вектор плоскости – определение, примеры, иллюстрации
Координаты нормального вектора плоскости – нахождение координат нормального вектора плоскости из уравнения плоскости
Как найти нормаль к плоскости по 3 точкам?
Уравнение плоскости по трем точкам
Общее уравнение плоскости и его исследование
🎥 Видео

Видео:Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать

Нормальный вектор плоскости – определение, примеры, иллюстрации

Чтобы материал легко усваивался, необходимо предварительно изучить теорию о прямой в пространстве и представление ее на плоскости и векторы.

Нормальным вектором плоскости считается любой ненулевой вектор, который лежит на перпендикулярной к данной плоскости прямой.

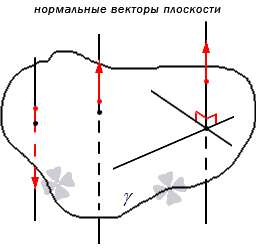
Отсюда следует, что имеет место существование большого количества нормальных векторов в данной плоскости. Рассмотрим на рисунке, приведенном ниже.

Нормальные векторы располагаются на параллельных прямых, поэтому они все коллинеарны. То есть, при нормальном векторе n → , расположенном в плоскости γ , вектор t · n → , имея ненулевое значение параметра t , также нормальный вектор плоскости γ . Любой вектор может быть рассмотрен как направляющий вектор прямой, которая перпендикулярна этой плоскости.

Имеются случаи совпадения нормальных векторов плоскостей из-за перпендикулярности одной из параллельных плоскостей, так как прямая перпендикулярна и второй плоскости. Отсюда следует, что нормальные векторы перпендикулярных плоскостей должны быть перпендикулярными.

Рассмотрим на примере нормального вектора на плоскости.

Задана прямоугольная система координат О х у z в трехмерном пространстве. Координатные векторы i → , j → , k → считаются нормальными векторами плоскостей O y z , O x z и O x y . Это суждение верно, так как i → , j → , k → ненулевые и расположены на координатных прямых O x , O y и O z . Эти прямые перпендикулярны координатным плоскостям O y z , O x z и O x y .

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Координаты нормального вектора плоскости – нахождение координат нормального вектора плоскости из уравнения плоскости

Статья предназначена для того, чтобы научить находить координаты нормального вектора плоскости при известном уравнении плоскости прямоугольной системы координат О х у z . Для определения нормального вектора n → = ( A , B , C ) в плоскости необходимо наличие общего уравнения плоскости, имеющее вид A x + B y + C z + D = 0 . То есть достаточно иметь уравнение плоскости, тогда появится возможность для нахождения координат нормального вектора.

Найти координаты нормального вектора, принадлежащего плоскости 2 x — 3 y + 7 z — 11 = 0 .

По условию имеем уравнение плоскости. Необходимо обратить внимание на коэффициенты, так как они и являются координатами нормального вектора заданной плоскости. Отсюда получаем, что n → = ( 2 , — 3 , 7 ) — это нормальный вектор плоскости. Все векторы плоскости задаются при помощи формулы t · n → = 2 · t , — 3 · t , 7 · t , t является любым действительным числом не равным нулю.

Ответ: n → = ( 2 , — 3 , 7 ) .

Определить координаты направляющих векторов заданной плоскости x + 2 z — 7 = 0 .

По условию имеем, что дано неполное уравнение плоскости. Чтобы увидеть координаты, необходимо преобразовать уравнение x + 2 z — 7 = 0 к виду 1 · x + 0 · y + 2 z — 7 = 0 . Отсюда получим, что координаты нормального вектора данной плоскости равны ( 1 , 0 , 2 ) . Тогда множество векторов будет иметь такую форму записи ( t , 0 , 2 · t ) , t ∈ R , t ≠ 0 .

Ответ: ( t , 0 , 2 · t ) , t ∈ R , t ≠ 0 .

При помощи уравнения плоскости в отрезках, имеющего вид x a + y b + z c = 1 , и общего уравнения плоскости возможна запись нормального вектора этой плоскости, где координаты равны 1 a , 1 b , 1 c .

Знания о нормальном векторе позволяют с легкостью решать задачи. Часто встречающимися задачами являются задания с доказательствами параллельности или перпендикулярности плоскостей. Заметно упрощается решение задач на составление уравнений заданной плоскости. Если имеется вопрос о нахождении угла между плоскостями или между прямой и плоскостью, то формулы нормального вектора и нахождения его координат помогут в этом.

Видео:Видеоурок "Уравнение плоскости по трем точкам"Скачать

Как найти нормаль к плоскости по 3 точкам?

Простой 1 комментарий

В вашем случае, если у вас есть 3 точки, принадлежащие плоскости

ну а дальше просто подставляете эти значения в формулу выше)))

ЗЫ: остается лишь определится с направлением нормали, которое зависит от соглашения по выбору и предоставлению точек A,B,C, которое к слову вы тут не озвучили.

Видео:1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

Уравнение плоскости по трем точкам

Содержание:

Вектором нормали к плоскости называется вектор, перпендикулярный к этой плоскости. Обозначать его будем буквой а буквами А, В, С будем обозначать координаты этого вектора (рис. 17). Составим уравнение плоскости, проходящей через известную точку с заданным нормальным вектором Пусть — текущая точка плоскости.

Т. к. вектор

Это уравнение плоскости по точке и нормальному вектору.

Если в (2.9) менять параметры А, В, С, т. е. менять координаты вектора нормали плоскости, то каждый раз будем получать уравнение другой плоскости, содержащей точку Множество всех таких плоскостей называется связкой плоскостей, проходящих через точку

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Пример 1:

Составить уравнение плоскости, проходящей через точку перпендикулярно к прямой Решение:

Т. к. плоскость должна быть перпендикулярна заданной прямой, то в качестве вектора нормали плоскости можно взять направляющий вектор прямой и тогда уравнение плоскости будет таким: или

Общее уравнение плоскости и его исследование

Рассмотрим уравнение плоскости по точке и нормальному вектору

и преобразуем его, собрав в одно слагаемое все постоянные

и, обозначив выражение в скобках одной буквой D, получим:

Возможно вам будут полезны данные страницы:

Это общее уравнение плоскости.

Равенство нулю отдельных коэффициентов этого уравнения вносит особенности в расположение плоскости.

1. D = 0. Уравнение принимает вид:

откуда ясно, что точка лежит на плоскости. Другими словами, плоскость проходит через начало координат.

2. А = 0. В таком случае Получилось, что направляющий вектор оси (вектор ) ортогонален вектору, т. е. плоскость параллельна оси Ох (рис. 18).

плоскость параллельна оси

плоскость парал- х лельна оси .

3. Плоскость параллельна и оси , и оси значит, она параллельна плоскости

— плоскость параллельна плоскости ;

— плоскость параллельна плоскости .

4. Первое условие означает, что плоскость параллельна оси , второе — что она проходит через начало координат. Значит, плоскость проходит через ось . — плоскость проходит через ось ;

— плоскость проходит через ось .

5. — координатные плоскости.

Пример 2:

Решение:

Т. к. в уравнении отсутствует перемещенная то плоскость параллельна оси .

Для построения этой плоскости сначала изобразим ее

«след» на плоскости Это — прямая, проходящая через две точки (5; 0; 0) и (0; 3; 0). Затем через полученную прямую проведем плоскость, параллельную оси (рис. 19).

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.