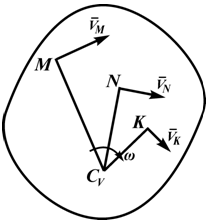
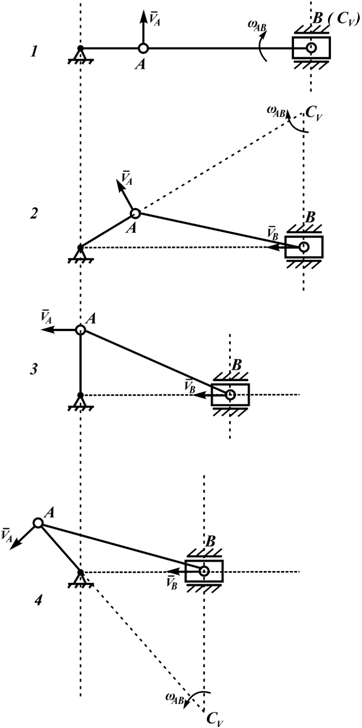
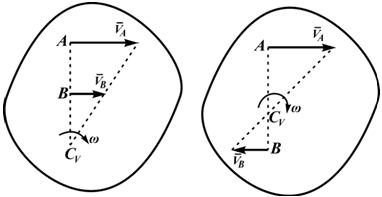
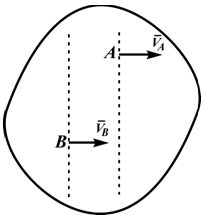
Как найти мгновенный центр скоростей если векторы этих скоростей параллельны (5 видео)

iSopromat.ru

Рассмотрим формулы и примеры определения положения мгновенного центра скоростей (МЦС) для различных твердых тел и механизмов при плоскопараллельном движении.

Теорема Эйлера-Шаля доказывает, что любое непоступательное перемещение фигуры в плоскости можно осуществить поворотом вокруг некоторого неподвижного центра.

В соответствии с этим легко доказывается, что при плоскопараллельном движении в каждый момент времени существует точка, неизменно связанная с плоской фигурой, скорость которой в этот момент равна нулю.

Эту точку называют мгновенным центром скоростей (МЦС). В учебниках эту точку пишут с индексом V, например P_V, C_V.

При определении положения МЦС скорость любой точки может быть записана: V_M = V_Cv + V_MCv , где точка C_V выбрана за полюс. Поскольку это МЦС и V_Cv=0, то скорость любой точки определяется как скорость при вращении вокруг мгновенного центра скоростей:

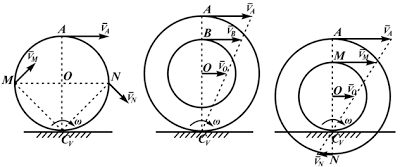
Из рисунка 2.16 видно, что МЦС лежит в точке пересечения перпендикуляров, проведённых к скоростям точек, при этом всегда справедливо соотношение:

На рисунке 2.17 показаны примеры определения положения МЦС детали кривошипно-шатунного механизма и приведены формулы для расчета скоростей точек.

На рисунках 2.18 — 2.21 приведены примеры определения положения МЦС.

В этом случае МЦС находится в «бесконечности», т.е.

V_A/2R=V₀/R=V_M/(R√2)=ω,
V_A/2R=V₀/R=V_B/(R+r)=ω,
V_A/(R+r)=V₀/r=V_N/(R-r)=ω

Формулы справедливы при отсутствии проскальзывания в точке C_V.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Содержание

Решение задач, контрольных и РГР
Набор студента для учёбы
Мгновенный центр скоростей (МЦС)
ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ. МГНОВЕННЫЙ ЦЕНТР СКОРОСТЕЙ. МГНОВЕННЫЙ ЦЕНТР УСКОРЕНИЙ
🌟 Видео

Видео:Мгновенный центр скоростейСкачать

Решение задач, контрольных и РГР

Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.

Если стоимость устроит вы сможете оформить заказ.

Видео:9.5. Мгновенный центр скоростейСкачать

Набор студента для учёбы

— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку

Видео:Мгновенный центр скоростейСкачать

Мгновенный центр скоростей (МЦС)

Зависимость (8.4) позволяет получить простую картину распределения скоростей точек плоской фигуры. Это распределение оказывается точно таким же, как и в случае тела, вращающегося вокруг неподвижной оси. Разница лишь в том, что точка, вокруг которой вращается плоская фигура, со временем изменяет свое положение, т.е. является мгновенным центром вращения.

Мгновенным центром скоростей (или мгновенным центром вращения) называют ту точку плоской фигуры, скорость которой в данный момент времени равна нулю. Покажем, что если угловая скорость фигуры отлична от нуля (со Ф 0), то такая точка существует и единственна.

Пусть в некоторый момент времени известна скорость _А точки А фигуры и угловая скорость фигуры со Ф 0.

Проведем прямую AN, перпендикулярную вектору Уд, и отложим на ней (рис. 8.8) отрезок

Найдем скорость точки Р фигуры при помощи векторной формулы (8.4):

Оба вектора в правой части этого равенства перпендикулярны к AN, т.с. параллельны друг другу, и направлены в противоположные стороны (рис. 8.8). Модули их равны, т.к. согласно (8.5)

Поэтому vр = у_л + у_Рд = 0, следовательно, точка Р является мгновенным центром скоростей (МЦС) фигуры. Единственность МЦС следует из процедуры его построения.

Пусть точка Р — мгновенный центр скоростей плоской фигуры, тогда скорость любой точки фигуры выражается в виде

Здесь _ВР — это вектор скорости точки В при вращении фигуры вокруг центра Р с угловой скоростью со, вектор _в = _ВР направлен перпендикулярно отрезку РВ в сторону вращения фигуры (рис. 8.9), а его величина согласно (8.5)

Это значит, что скорость любой точки фигуры находится так, как если бы фигура вращалась в своей плоскости с угловой скоростью со вокруг МЦС (рис. 8.9).

Из равенств v_B = со ? ВР и v_c = со- СР следует пропорция

т.е. величина скорости точки плоской фигуры пропорциональна её расстоянию от МЦС.

Для решения задач кинематики плоского движения удобно пользоваться следующими правилами построения МЦС.

1. Как видно из рис. 8.9, МЦС — это точка пересечения перпендикуляров к скоростям точек плоской фигуры. Поэтому для построения МЦС достаточно знать направления скоростей двух точек фигуры (при условии, что эти скорости непараллельны).

2. Если скорости двух точек фигуры параллельны, а сами эти точки лежат на общем перпендикуляре к скоростям (рис. 8.10), то положение МЦС можно установить при помощи пропорции (8.9), если известны величины и направления скоростей. Решение пропорции (8.9) можно заменить простым геометрическим построением, показанным на рис. 8.9 штриховой линией: МЦС находится как точка пересечения общего перпендикуляра ВС и линии, соединяющей концы векторов скоростей точек В и С.

3. Если перпендикуляры к скоростям точек параллельны, т.е. не имеют пи одной общей точки (рис. 8.11), то МЦС построить невозможно. Построения (п.8.4) допускают такую ситуацию лишь в том случае, когда угловая скорость фигуры со = 0. Тогда из (8.4) и (8.5) следует, что все точки фигуры имеют одинаковые скорости.

4. Если известна скорость _А какой-нибудь точки А фигуры и угловая скорость фигуры со, то можно найти МЦС, повторяя построения п. 4.4.
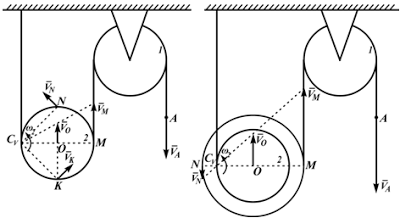
5. При качении фигуры по неподвижной кривой без проскальзывания МЦС фигуры находится в точке К её касания с этой кривой (рис. 8.12), так как скорость точки касания фигуры равна нулю.

Продемонстрируем использование МЦС для расчета скоростей.

Пример 2. Стержень АВ длиной 0,6 м совершает плоскопараллельное движение так, что его концы А и В перемещаются вдоль вертикальРешение. Найдем положение МЦС стержня АВ. Для этого построим перпендикуляры к скоростям точек А и В (рис. 8.14). Точка пересечения Р этих перпендикуляров и является МЦС стержня.

ной и горизонтальной направляющих (рис. 8.13). Известно, что точка А движется с постоянной скоростью гд = 2 м/с.

Найти угловую скорость стержня АВ и скорость точки В в тот момент времени, когда угол (р= 30°.

Согласно описанным выше свойствам МЦС (и. 8.4) имеем:

Из первого равенства находим угловую скорость стержня

Из второго равенства определяем величину скорости точки В:

Направления скоростей у_д , v_в и направление вращения стержня А В согласованы так, как показано на рис. 8.14.

Видео:Мгновенный центр скоростей и кинетическая энергия колесаСкачать

ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ. МГНОВЕННЫЙ ЦЕНТР СКОРОСТЕЙ. МГНОВЕННЫЙ ЦЕНТР УСКОРЕНИЙ

Плоскопараллельным/плоским движением ATT называется такое движение, при котором все точки тела движутся в плоскостях, параллельных некоторой неподвижной плоскости.

При таком движении все точки тела, расположенные на одном перпендикуляре к неподвижной плоскости, движутся одинаково (рис. 3.1). Поэтому для изучения движения всего тела достаточно изучить, как движется сечение S тела плоскостью Оху, параллельной неподвижной плоскости П. В дальнейшем плоскость сечения изображается плоскостью рисунка, а вместо всего тела изображается только сечение S (рис. 3.2). Положение сечения S можно определить положением любого отрезка АВ этого сечения, а положение такого отрезка можно определить, зная три величины: х_А, у_А, z_A— Точка А, выбранная для определения положения плоской фигуры S, называется полюсом движения. На рис. 3.2 дана неподвижная СО Оху и подвижная СО Аrj, жестко связанная с изучаемым сечением (начало этой СО закреплено в выбранном полюсе движения, в точке А), ср — угол поворота подвижной оси абсцисс At, относительно неподвижной оси абсцисс Ох.

Рис. 3.1. К определению плоского движения

Рис. 3.2. Кинематические характеристики плоского движения

Таким образом, чтобы знать закон плоского движения, надо знать зависимости:

которые называются (кинематическими) уравнениями плоского движения [1] твердого тела.

В частности, можно задать эти уравнения в виде:

Перемещение плоской фигуры в ее плоскости можно осуществить путем поступательного перемещения вместе с полюсом и вращения вокруг этого полюса (или, можно сказать, вокруг оси, проходящей через полюс перпендикулярно плоскости движения). При этом угол поворота не зависит от выбора полюса. Эти утверждения являются фактически формулировкой основной теоремы кинематики для частного случая плоского движения. Следовательно, все формулы гл. К. 2 для вычисления положений, скоростей и ускорений точек остаются справедливыми и в случае плоского движения, в частности:

Таким образом, скорость любой точки А/тела складывается геометрически из скорости полюса v_A и скорости вращения вокруг этого полюса v_AM (рис. 3.3). Поэтому v_AM всегда перпендикулярна линии ЛМ,

а по модулю v_AM = со • АМ. Ускорение точки а_м складывается из геометрической суммы трех векторов: ускорения а_А поступательного движения полюса и ускорения а_АМ вращения этой точки вокруг полюса, которое раскладывается на две составляющие — осестремительное [2] а°_А с _м и вращательное a’J_M. При этом вектор а°_АМ направлен всегда от точки М к полюсу — точке А, а вектор а_А р _м направлен перпендикулярно АМ в сторону движения точки, если точка движется ускоренно, и в противоположную сторону, если точка движется замедленно.

Рис. 3.3. Сложение скоростей при плоском движении

? Часто бывает удобным пользоваться теоремой о проекциях скоростей двух точек тела:

Проекции скоростей любых двух точек ATT на прямую, соединяющую эти точки, всегда равны друг другу. Щ>_аву_{а = np_ABv_B, или в других обозначениях (у_А)_ЛВ} = (v_B)_AB.

Доказательство проведем от противного (рис. 3.4). Если бы v_A cos а не равнялось v_ficos (3, то точки А и В двигались бы вдоль прямой АВ с разными скоростями и, следовательно, ав * const. Но это невозможно, так как это означало бы, что ATT деформируется. ?

Рис. 3.4. К теореме о проекциях скоростей двух точек ATT на прямую, соединяющую их

Эта теорема позволяет легко находить скорость любой точки тела, если известны ее направление и скорость любой другой точки тела.

? Мгновенным центром скоростей называется точка Р тела или жестко связанная с ним, скорость которой равна нулю в данный момент времени.

Легко убедиться, что если тело движется не поступательно, то такая точка в каждый данный момент времени существует, и притом она единственная. Пусть в момент времени t точка А тела имеет скорость v_A и точка В — v_B, при этом эти скорости не параллельны друг другу (рис. 3.5).

Рис. 3.5. Частный случай определения мгновенного центра скоростей точки Р

Тогда точка Р пересечения перпендикуляров, восстановленных к скоростям v_A и v_B в точках А и В, и будет мгновенным центром скоростей тела в этот момент времени. Действительно, если допустить, что v_p ф 0, то по теореме о проекциях скоростей двух точек необходимо, чтобы v_P ± АР и v_P ± ВР. Но это невозможно, так как АР не параллельна ВР.

Если принять за полюс мгновенный центр скоростей — точку Р, то имеем v_M = v_p + v_PM = v_PM. Следовательно, скорость любой точки тела равна ее вращательной скорости вокруг мгновенного центра скоростей. При этом модули скоростей точек тела прямо пропорциональны их расстояниям до мгновенного центра скоростей (рис. 3.6), так как v_M = со • РМ.

Способы нахождения мгновенного центра скоростей

1. Если плоское движение — качение без скольжения подвижного цилиндрического тела по поверхности другого неподвижного цилиндрического тела (рис. 3.7), то мгновенный центр скоростей — точка касания этих тел (так как при отсутствии скольжения точки касания тел должны иметь одинаковые скорости, а второе тело неподвижно).

Рис. 3.6. Мгновенное распределение скоростей вокруг мгновенного центра скоростей

Рис. 3.7. Способ определения мгновенного центра скоростей: при качении по неподвижной опоре

2. Если заданы направления скоростей двух точек и при этом эти направления не параллельны (рис. 3.8), то мгновенный центр скоростей — точка пересечения перпендикуляров, восстановленных к направлениям скоростей в самих точках.

Рис. 3.8. Один из способов определения мгновенного центра скоростей: при непараллельных скоростях точек тела

3. Если заданы скорости двух точек и при этом направления скоростей параллельны, модули различны и ЛВ перпендикулярна линиям скоростей (рис. 3.9), то мгновенный центр скоростей — точка пересечения прямых, проведенных через начала и концы векторов скоростей (начало — с началом, конец — с концом).

Рис. 3.9. Один из способов определения мгновенного центра скоростей: при параллельных скоростях двух точек тела

4. Если заданы скорости двух точек и при этом направления скоростей параллельны, а ЛВ не перпендикулярна линиям скоростей, то мгновенный центр скоростей находится в бесконечности, т.е. тело движется поступательно в этот момент времени (со = 0). Это следует из теоремы о проекциях скоростей двух точек: v_B = v_Aи скорости всех точек параллельны скорости v_A.
5. Если задана скорость одной точки плоской фигуры v_M и мгновенная угловая скорость со, то имеем для мгновенного центра скоростей формулы v_M = v_PM и v_M = со • РМ (рис. ЗЛО). Следовательно, мгновенный центр скоростей находится на перпендикуляре, восстановленном из точки М, на расстоянии PM = v_M/co.

Рис. 3.10. Один из способов определения мгновенного центра скоростей: по скорости одной точки и модулю угловой скорости тела

? Поскольку скорости сечения S распределены в каждый момент времени так, как если бы движение S представляло собой вращение вокруг неподвижной точки Р (являющейся мгновенным центром скоростей), то точку неподвижной плоскости, совпадающую с Р, часто называют мгновенным центром вращения, а ось P_z, перпендикулярную плоскости сечения 5, — мгновенной осью вращения тела. От неподвижной оси и центра мгновенная ось и центр отличаются тем, что они все время меняют свое положение в пространстве. Если наклеить на фигуру, совершающую плоское движение, лист бумаги и в каждый момент времени прокалывать иглой мгновенный центр скоростей, то получатся две серии отметок: одна на неподвижной плоскости, другая на листе, связанном с фигурой.

Геометрическое место мгновенных центров скоростей, отмеченных на неподвижной плоскости, называется неподвижной центрои- дой/полодией/полоидой.

Геометрическое место мгновенных центров скоростей, отмеченных на подвижной плоскости, жестко связанной с фигурой, называется подвижной центроидой/полодией/полоидой.

При качении цилиндра по горизонтальной плоскости (рис. 3.11) неподвижная центроида — горизонтальная прямая, а подвижная — окружность. В каждый момент времени подвижная и неподвижная центроиды имеют общую точку касания — мгновенный центр скоростей Р, т.е. точку, скорость которой равна нулю. Поэтому плоское движение можно представить как качение без скольжения подвижной центроиды по неподвижной (теорема Пуансо, которая часто применяется в кинематике машин и механизмов).

Рис. 3.11. Неподвижная (точки с индексом н) и подвижная (точки без индекса) центроиды/полоиды, образующиеся при качении цилиндра

по горизонтальной плоскости. Соответственно — прямая и окружность

Чтобы составить уравнение центроиды, продифференцируем уравнения (3.1а), учтя, что v_p = 0:

Откуда получаем уравнения неподвижной центроиды в параметрической форме:

Подставляя эти значения х_р и у_р в уравнения (3.1а), найдем уравнения подвижной центроиды в параметрической форме:

? Мгновенным центром ускорений называется точка Q тела или жестко связанная с ним, ускорение которой равно нулю в данный момент времени: a_Q = 0.

Если принять за полюс мгновенный центр ускорений — точку Q, то имеем а_м = a_Q + a_QM = a_QM. Следовательно, ускорение любой точки тела равно ее вращательному ускорению вокруг мгновенного центра ускорений. При этом модули ускорений точек тела прямо пропорциональны их расстояниям до мгновенного центра ускорений.

Рассмотрим способы нахождения мгновенного центра ускорений:

1) пусть задано ускорение полюса А и мгновенные угловые скорость со и ускорение ? (рис.3.12). Тогда a_Q = а_А + a_AQ = 0, откуда а_А = —a_AQ = 0 и . Следовательно, отрезок

и составляет угол а с ускорением полюса, тангенс

которого равен Угол ос откладывается от ускорения полюса а_А в сторону вращения тела в случае ускоренного вращения, если е > 0, и в противоположную сторону, если ? Ъ Ав +а °Ав) • В этом уравнении вектор а_А известен. Известен также вектор а°_АМ, который направлен от точки В к точке А, а его модуль равен

где ab берется на плане скоростей. Направления векторов и aJ_B известны: направление а_в задано, вектор а_А р _в направлен перпендикулярно АВ. Поэтому уравнение плоского движения для а_в можно решить графически следующим образом.

Из полюса построения q проводим вектор qa_x = а_А. От его конца откладываем вектор qb™=a Q _AB. Через точку Ь™ проводим прямую, перпендикулярную АВ (вдоль которой направлен вектор а в _А р _в), а через точку q проводим прямую, параллельную заданному направлению В В’ вектора а_в, до их взаимного пересечения в точке А,. Тогда А^А, = а™_в и qb_x = а_в.

Для определения ускорения точки С можно написать два уравнения:

В первом уравнении нам известен вектор а_А и вектор а°_АС (он направлен от С к И, а его модуль равен , где ас берется на плане

скоростей), а также направление вектора а_А р _с (он направлен перпендикулярно АС). Но вектор а_с не известен ни по модулю, ни по направлению. Поэтому первое уравнение нельзя решить графически. Точно так же нельзя решить и второе уравнение: в него входит искомый вектор а_с и вектор а^_с, неизвестный по модулю.

Поэтому преобразуем систему (*.1):

В этом уравнении известны векторы а, а_в, а°_АС, а°_вс (последний направлен от С к В, а его модуль равен , где Ас берется

на плане скоростей) и известно направление векторов а_А р _с и a R _B p _c. Следовательно, уравнение (*.2) можно решить графически.

От вектора qa_x = а_л откладываем вектор а,с“ = а°_АВ и через с™ проводим прямую, перпендикулярную АС (вдоль этой прямой будет направлен вектор а»_АС и, следовательно, на этой прямой будет лежать конец вектора а_с). Аналогично от вектора qb_i = а_и откладываем вектор Ь_хс™ = а°_вс и через с” с проводим прямую, перпендикулярную ВС (вдоль этой прямой будет направлен вектор а в ^_с и, следовательно, на этой прямой будет лежать конец вектора а_с). На пересечении этих прямых — точке с, — и лежит конец вектора а_с. То есть qc_x = а_с.

На плане ускорений векторы я,А, = а_АВ, а,с, = а_АС и А,с, = а_вс суть ускорения точек В и С, обусловленные вращением фигуры вокруг соответственных полюсов, причем:

Построив план ускорений, легко показать, что фигура оДс, подобна фигуре АВС и повернута относительно нее на угол (л — а), где а определяется из формулы:

Действительно, согласно (*.3) отрезки треугольника а_хЬ_хс_х пропорциональны отрезкам треугольника ЛВС, следовательно, Да_хЬ_хс_х

Если из плана скоростей можно определить угловую скорость плоской фигуры, то из плана ускорений можно определить угловое ускорение плоской фигуры. Действительно, так как b_x^b_x = а_А р _в = е ? АВ, то