Как найти косинус бета для вектора (7 видео)

Направляющие косинусы вектора.

Содержание

Определение направляющих косинусов
Формулы вычисления направляющих косинусов вектора
Формула вычисления направляющих косинусов вектора для плоских задач
Формула вычисления направляющих косинусов вектора для пространственных задач
Примеры задач с направляющими косинусами вектора
Примеры плоских задач с направляющими косинусами вектора
Примеры пространственных задач с направляющими косинусами вектора
Нахождение угла между векторами
Нахождение угла между векторами
Как найти косинус угла между векторами
Формула
Примеры вычисления косинуса угла между векторами
🎥 Видео

Видео:Косинус угла между векторами. Коллинеарность векторовСкачать

Определение направляющих косинусов

Направляющие косинусы однозначно задают направление вектора.

Соответственно, координаты единичного вектора равны его направляющим косинусам.

Видео:§7 Направляющие косинусы вектораСкачать

Формулы вычисления направляющих косинусов вектора

Формула вычисления направляющих косинусов вектора для плоских задач

В случае плоской задачи (рис. 1) направляющие косинусы вектора a = < a_x ; a_y > можно найти воспользовавшись следующей формулой

cos α =	a_x	;	cos β =	a_y
	\| a \|			\| a \|

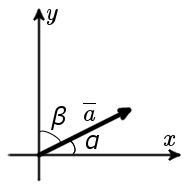рис. 1

Формула вычисления направляющих косинусов вектора для пространственных задач

В случае пространственной задачи (рис. 2) направляющие косинусы вектора a = < a_x ; a_y ; a_z > можно найти воспользовавшись следующей формулой

cos α =	a_x	;	cos β =	a_y	;	cos γ =	a_z
	\| a \|			\| a \|			\| a \|

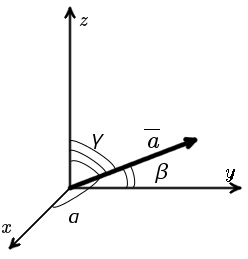рис. 2

Видео:Угол между векторами | МатематикаСкачать

Примеры задач с направляющими косинусами вектора

Примеры плоских задач с направляющими косинусами вектора

Найдем модуль вектора a :
| a | = √ 3 2 + 4 2 = √ 9 + 16 = √ 25 = 5.

Найдем направляющие косинусы вектора a :

cos α =	a_x	=	3	= 0.6
	\| a \|		5

cos β =	a_y	=	4	= 0.8
	\| a \|		5

Ответ: направляющие косинусы вектора cos α = 0.6, cos β = 0.8.

a_x = | a | · cos α = 26 · 5 13 = 10
a_y = | a | · cos β = 26 · (- 12 13 ) = -24

Примеры пространственных задач с направляющими косинусами вектора

Найдем модуль вектора a :
| a | = √ 2 2 + 4 2 + 4 2 = √ 4 + 16 + 16 = √ 36 = 6.

Найдем направляющие косинусы вектора a :

cos α =	a_x	=	2	=	1
	\| a \|		6		3

cos β =	a_y	=	4	=	2
	\| a \|		6		3

cos γ =	a_z	=	4	=	2
	\| a \|		6		3

Ответ: направляющие косинусы вектора cos α = 1 3 , cos β = 2 3 , cos γ = 2 3 .

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Видео:#вектор Разложение вектора по ортам. Направляющие косинусыСкачать

Нахождение угла между векторами

Длина вектора, угол между векторами – эти понятия являются естественно-применимыми и интуитивно понятными при определении вектора как отрезка определенного направления. Ниже научимся определять угол между векторами в трехмерном пространстве, его косинус и рассмотрим теорию на примерах.

Для рассмотрения понятия угла между векторами обратимся к графической иллюстрации: зададим на плоскости или в трехмерном пространстве два вектора a → и b → , являющиеся ненулевыми. Зададим также произвольную точку O и отложим от нее векторы O A → = b → и O B → = b →

Углом между векторами a → и b → называется угол между лучами О А и О В .

Полученный угол будем обозначать следующим образом: a → , b → ^

Очевидно, что угол имеет возможность принимать значения от 0 до π или от 0 до 180 градусов.

a → , b → ^ = 0 , когда векторы являются сонаправленными и a → , b → ^ = π , когда векторы противоположнонаправлены.

Векторы называются перпендикулярными, если угол между ними равен 90 градусов или π 2 радиан.

Если хотя бы один из векторов является нулевым, то угол a → , b → ^ не определен.

Видео:Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать

Нахождение угла между векторами

Косинус угла между двумя векторами, а значит и собственно угол, обычно может быть определен или при помощи скалярного произведения векторов, или посредством теоремы косинусов для треугольника, построенного на основе двух данных векторов.

Согласно определению скалярное произведение есть a → , b → = a → · b → · cos a → , b → ^ .

Если заданные векторы a → и b → ненулевые, то можем разделить правую и левую части равенства на произведение длин этих векторов, получая, таким образом, формулу для нахождения косинуса угла между ненулевыми векторами:

cos a → , b → ^ = a → , b → a → · b →

Данная формула используется, когда в числе исходных данных есть длины векторов и их скалярное произведение.

Исходные данные: векторы a → и b → . Длины их равны 3 и 6 соответственно, а их скалярное произведение равно — 9 . Необходимо вычислить косинус угла между векторами и найти сам угол.

Решение

Исходных данных достаточно, чтобы применить полученную выше формулу, тогда cos a → , b → ^ = — 9 3 · 6 = — 1 2 ,

Теперь определим угол между векторами: a → , b → ^ = a r c cos ( — 1 2 ) = 3 π 4

Ответ: cos a → , b → ^ = — 1 2 , a → , b → ^ = 3 π 4

Чаще встречаются задачи, где векторы задаются координатами в прямоугольной системе координат. Для таких случаев необходимо вывести ту же формулу, но в координатной форме.

Длина вектора определяется как корень квадратный из суммы квадратов его координат, а скалярное произведение векторов равно сумме произведений соответствующих координат. Тогда формула для нахождения косинуса угла между векторами на плоскости a → = ( a x , a y ) , b → = ( b x , b y ) выглядит так:

cos a → , b → ^ = a x · b x + a y · b y a x 2 + a y 2 · b x 2 + b y 2

А формула для нахождения косинуса угла между векторами в трехмерном пространстве a → = ( a x , a y , a z ) , b → = ( b x , b y , b z ) будет иметь вид: cos a → , b → ^ = a x · b x + a y · b y + a z · b z a x 2 + a y 2 + a z 2 · b x 2 + b y 2 + b z 2

Исходные данные: векторы a → = ( 2 , 0 , — 1 ) , b → = ( 1 , 2 , 3 ) в прямоугольной системе координат. Необходимо определить угол между ними.

Решение

Для решения задачи можем сразу применить формулу:

cos a → , b → ^ = 2 · 1 + 0 · 2 + ( — 1 ) · 3 2 2 + 0 2 + ( — 1 ) 2 · 1 2 + 2 2 + 3 2 = — 1 70 ⇒ a → , b → ^ = a r c cos ( — 1 70 ) = — a r c cos 1 70

Также можно определить угол по формуле:

cos a → , b → ^ = ( a → , b → ) a → · b → ,

но предварительно рассчитать длины векторов и скалярное произведение по координатам: a → = 2 2 + 0 2 + ( — 1 ) 2 = 5 b → = 1 2 + 2 2 + 3 2 = 14 a → , b → ^ = 2 · 1 + 0 · 2 + ( — 1 ) · 3 = — 1 cos a → , b → ^ = a → , b → ^ a → · b → = — 1 5 · 14 = — 1 70 ⇒ a → , b → ^ = — a r c cos 1 70

Ответ: a → , b → ^ = — a r c cos 1 70

Также распространены задачи, когда заданы координаты трех точек в прямоугольной системе координат и необходимо определить какой-нибудь угол. И тогда, для того, чтобы определить угол между векторами с заданными координатами точек, необходимо вычислить координаты векторов в виде разности соответствующих точек начала и конца вектора.

Исходные данные: на плоскости в прямоугольной системе координат заданы точки A ( 2 , — 1 ) , B ( 3 , 2 ) , C ( 7 , — 2 ) . Необходимо определить косинус угла между векторами A C → и B C → .

Решение

Найдем координаты векторов по координатам заданных точек A C → = ( 7 — 2 , — 2 — ( — 1 ) ) = ( 5 , — 1 ) B C → = ( 7 — 3 , — 2 — 2 ) = ( 4 , — 4 )

Теперь используем формулу для определения косинуса угла между векторами на плоскости в координатах: cos A C → , B C → ^ = ( A C → , B C → ) A C → · B C → = 5 · 4 + ( — 1 ) · ( — 4 ) 5 2 + ( — 1 ) 2 · 4 2 + ( — 4 ) 2 = 24 26 · 32 = 3 13

Ответ: cos A C → , B C → ^ = 3 13

Угол между векторами можно определить по теореме косинусов. Отложим от точки O векторы O A → = a → и O B → = b → , тогда, согласно теореме косинусов в треугольнике О А В , будет верным равенство:

A B 2 = O A 2 + O B 2 — 2 · O A · O B · cos ( ∠ A O B ) ,

b → — a → 2 = a → + b → — 2 · a → · b → · cos ( a → , b → ) ^

и отсюда выведем формулу косинуса угла:

cos ( a → , b → ) ^ = 1 2 · a → 2 + b → 2 — b → — a → 2 a → · b →

Для применения полученной формулы нам нужны длины векторов, которые несложно определяются по их координатам.

Хотя указанный способ имеет место быть, все же чаще применяют формулу:

Видео:Задача 3. Найти косинус угла между векторами.Скачать