Как найти длину разности векторов изображенных на клетчатой бумаге

Геометрия | 5 — 9 классы

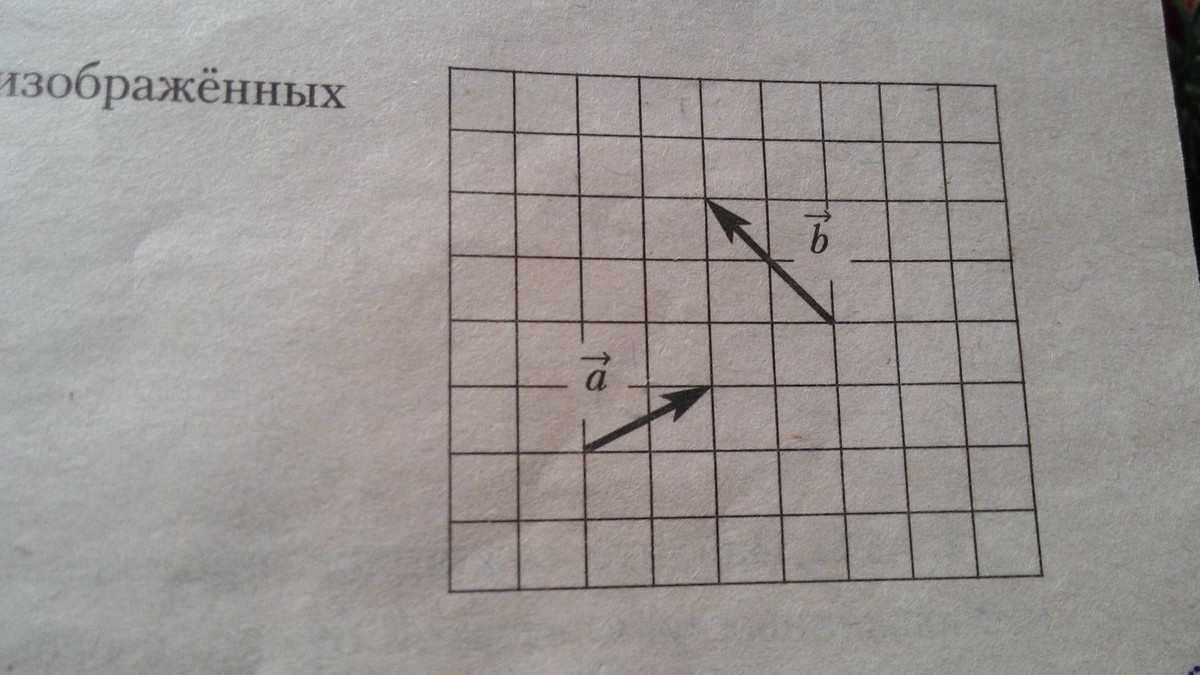
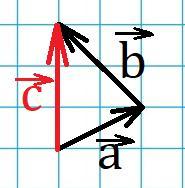
Найдите длину суммы векторов a и b, изображенных на клетчатой бумаге с размером клетки 1 на 1.

Длина $displaystyle vec$ равна 3·1 = 3 т.

К. размер клетки 1 на 1.

Видео:ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать

Найдите площадь трапеции , изображенной на клетчатой бумаге с размером клетки 1см× 1см Ответ дайте в квадратных см?

Найдите площадь трапеции , изображенной на клетчатой бумаге с размером клетки 1см× 1см Ответ дайте в квадратных см.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см х 1 см?

Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см х 1 см.

Видео:Вычитание векторов. 9 класс.Скачать

На клетчатой бумаге с размером клетки 1×1 изоброжена трапеция ?

На клетчатой бумаге с размером клетки 1×1 изоброжена трапеция .

Найдите длину ее средней линии.

Видео:Найдите площадь треугольника изображенного на клетчатой бумаге с размером клетки 1х1 см.Скачать

На клетчатой бумаге с размером клетки 1х1 изображена трапеция?

На клетчатой бумаге с размером клетки 1х1 изображена трапеция.

Найдите длину её средней линии.

Видео:Самый простой способ нахождения площадиСкачать

Найдите (в см ^ 2) площадь многоугольника, изображенного на клетчатой бумаге с размером клетки 1 см× 1 см?

Найдите (в см ^ 2) площадь многоугольника, изображенного на клетчатой бумаге с размером клетки 1 см× 1 см.

Видео:егэ векторы решу егэ все задания №2 профильСкачать

Найдите (в см ^ 2) площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1× 1 см?

Найдите (в см ^ 2) площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1× 1 см.

Видео:Построить разность векторов.Скачать

Найдите (в см ^ 22) площадь многоугольника, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см?

Найдите (в см ^ 22) площадь многоугольника, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см.

Видео:Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать

Найдите (в см ^ 2) площадь многоугольника, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см?

Найдите (в см ^ 2) площадь многоугольника, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см.

Видео:Нахождение длины вектора. Практическая часть. 9 класс.Скачать

Найдите (в см ^ 2) площадь многоугольника, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см?

Найдите (в см ^ 2) площадь многоугольника, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см.

Видео:ОГЭ 2019 Задание 19. Геометрия на клетчатой бумаге. Площади.Скачать

На клетчатой бумаге с размером клетки 1х1 изображён прямоугольный треугольник Найдите длину его гипотенузы?

На клетчатой бумаге с размером клетки 1х1 изображён прямоугольный треугольник Найдите длину его гипотенузы.

На этой странице вы найдете ответ на вопрос Найдите длину суммы векторов a и b, изображенных на клетчатой бумаге с размером клетки 1 на 1?. Вопрос соответствует категории Геометрия и уровню подготовки учащихся 5 — 9 классов классов. Если ответ полностью не удовлетворяет критериям поиска, ниже можно ознакомиться с вариантами ответов других посетителей страницы или обсудить с ними интересующую тему. Здесь также можно воспользоваться «умным поиском», который покажет аналогичные вопросы в этой категории. Если ни один из предложенных ответов не подходит, попробуйте самостоятельно сформулировать вопрос иначе, нажав кнопку вверху страницы.

Видео:Выразить векторы. Разложить векторы. Задачи по рисункам. ГеометрияСкачать

Задание по геометрии — вектора.

Эта страница посвящена группе задач по геометрии, связанной с векторами, и является продолжением рассмотрения серии геометрических заданий, характерных для ЕГЭ и ОГЭ по математике.
Если вы не занимались другими типами этого задания, перейдите по ссылкам в конце страницы.

Видео:Сложение векторов. 9 класс.Скачать

Задачи на вектора.

Длина отрезка называется модулем вектора. Два вектора равны, если они имеют равные модули и одинаково направлены.
Вектора обозначают либо строчными латинскими буквами a, b, c . , либо указанием концов отрезка AB, CD, MN. Чтобы отличить обозначение вектора от обозначения просто отрезка, эти символы сверху дополняются черточками или стрелочками. В печатном тексте строчные латинские буквы часто выделяют только полужирным шрифтом.

Если вектор обозначен двумя буквами (концами отрезка), то на первом месте всегда стоит начало вектора.

Задать вектор можно разными способами:
1. Графически — изобразить на координатной сетке.
2. Задать начальную и конечную точки и их координаты.
3. Задать длину отрезка и направление. Направление определяют углы с осями координат (направляющие косинусы).
4. Задать координаты вектора.

Уточним понятие координаты вектора.

На рисунке вектор AB имеет координаты (9;5). Обратите внимание, что эти числа фактически задают катеты прямоугольного треугольника, гипотенузой которого является отрезок АВ. Длина этих катетов не изменится, если мы переместим параллельным переносом отрезок, а с ним и весь треугольник, в другое место. Координаты вектора не зависят от его положения на плоскости, а только от длины отрезка и направления. Если направление вектора не совпадает с направлением оси координат, то соответствующая координата вектора будет равна длине катета со знаком «минус».

Вектора можно складывать, вычитать, умножать на число. Для векторов также определены специальные виды умножения — скалярное произведение, результатом которого является число, и — векторное произведение, результатом которого является вектор. (Векторное произведение не входит в обязательную школьную программу по математике, но частично встречается на уроках физики, когда изучают законы индукции магнитного поля.) Операции над векторами можно производить либо координатным методом, либо графическим (правило параллелограмма, правило треугольника. ). Повторите эти правила по учебнику или справочнику и выберите себе «любимое». Я привожу решение тем методом, который короче для конкретной задачи.

Для следующей группы задач чертёж в условии, вообще говоря, не обязателен. Если решать задачи координатным методом, то и в решении можно обойтись без чертежа, тем более, не нужна сетка. Однако лучше чертежи делать всегда, чтобы избежать нечаянных ошибок. А сетка помогает зрительно контролировать своё решение. Конечно, в том случае, если масштаб данных позволяет.

Две стороны прямоугольника ABCD равны 6 и 8.
Найдите длину вектора AC .

Длина вектора AC — равна длине отрезка AC, который является гипотенузой прямоугольного треугольника ABC с известными катетами.
AC 2 = AB 2 + BC 2 = 8 2 + 6 2 = 64 + 36 = 100; AC = 10.

Ответ: 10

Две стороны прямоугольника ABCD равны 6 и 8.
Найдите длину суммы векторов AB и AD .

По правилу параллелограмма: сумма векторов совпадает с диагональю параллелограмма, проходящей через точку, в которой совмещены начала векторов-слагаемых; начало вектора-суммы находится в точке начала обоих векторов. На рисунке это вектор AC — . Его длину мы находили в предыдущей задаче:
AC 2 = AB 2 + BC 2 = 8 2 + 6 2 = 64 + 36 = 100; AC = 10.

Ответ: 10

Две стороны прямоугольника ABCD равны 6 и 8.
Найдите длину разности векторов AB и AD .

По правилу параллелограмма: разность векторов совпадает с другой диагональю параллелограмма (соединяющей концы векторов-слагаемых, если их начала совмещены в одной точке); вектор разности направлен от вычитаемого к уменьшаемому. На рисунке это вектор DB — , направлен от D к B, так как я нахожу разность AB — − AD — .
DB 2 = AB 2 + AD 2 = 8 2 + 6 2 = 64 + 36 = 100; DB = 10.

Ответ: 10

Замечание: Ответы совпали, потому что дан один и тот же прямоугольник, а диагонали в прямоугольнике, как известно, равны.

Две стороны прямоугольника ABCD равны 6 и 8.
Найдите скалярное произведение векторов AB и AD .

Скалярное произведение двух векторов a и b находится по любой из двух формул.
1) Через координаты по формуле (a,b) = a₁·b₁ + a₂·b₂
2) Через длины векторов и угол между ними по формуле (a,b) = |a|·|b|·cosα

Способ I.
Координаты вектора AB — равны (8;0), вектора AD — равны (0;6).
Значит ( AB — , AD — ) = 8·0 + 0·6 = 0.
Способ II.
| AB — | = AB = 8, | AD — | = AD = 6, cosα = cos∠DAB = cos90° = 0.
Значит ( AB — , AD — ) = | AB — |·| AD — |·cos∠DAB = 8·6·0 = 0.

Ответ: 0

Замечание: Есть несколько способов обозначения скалярного произведения. Можно со скобками (a,b) или без них a·b _ _ , как обычное умножение.

Две стороны прямоугольника ABCD равны 6 и 8.
Диагонали пересекаются в точке O. Найдите длину суммы векторов AO и BO .

Вспомним, что диагонали прямоугольника пересекаются в его центре и в точке пересечения делятся пополам.

Способ I.
Координаты вектора AO — равны (4;3), обе положительны, потому что вектор направлен вверх, как ось Oy и вправо, как ось Ox. Координаты вектора BO — равны (-4;3), вектор направлен вверх, как ось Oy, но влево, противоположно оси Ox. Чтобы найти сумму векторов, воспользуемся тем, что при сложении векторов их соответствующие координаты складываются. Пусть вектор s(s₁;s₂) — сумма, тогда s₁ = 4 + (- 4) = 4 — 4 = 0; s₂ = 3 + 3 = 6. Квадрат длины вектора |s| 2 = s₁ 2 + s₂ 2 = 0 2 + 6 2 = 36;
длина вектора |s| = 6.

Способ II.
Чтобы решить задачу графически, надо применить к одному или к обоим векторам параллельный перенос. Для применения правила параллелограмма надо сместить их так, чтобы обе начальные точки совпали. Для применения правила треугольника надо начало одного из векторов-слагаемых совместить с концом другого. Здесь сместили вектор BO — вдоль линии ВD. На рисунке показан результат графического сложения — это вектор AD — . Как видно непосредственно по рисунку, его длина равна 6.

Ответ: 6

Две стороны прямоугольника ABCD равны 6 и 8.
Диагонали пересекаются в точке O. Найдите длину разности векторов AO и BO .

‘Способ I.
Координаты вектора AO — равны (4;3), вектора BO — равны (-4;3). Чтобы найти разность векторов, нужно найти разность их соответствующих координат. Пусть вектор d(d₁;d₂) — разность, тогда d₁ = 4 — (- 4) = 4 + 4 = 8; d₂ = 3 — 3 = 0. Квадрат длины вектора |d| 2 = d₁ 2 + d₂ 2 = 8 2 + 0 2 = 64; длина вектора |d| = 8.

Способ II.
Чтобы решить задачу графически, совмещаем начала векторов параллельным переносом обоих векторов вдоль диагоналей прямоугольника. На рисунке показан результат графического вычитания — это вектор DС — . Как видно непосредственно по рисунку, его длина равна 8.

Ответ: 8

Продолжить и повторить решение типовых задач ЕГЭ по математике на темы:

Перейдите по стрелке, чтобы найти ссылки на другие задачи ЕГЭ по математике.

Видео:9 класс, 2 урок, Координаты вектораСкачать

Векторы на плоскости Работу выполнила Нина Саидзода. — презентация

Презентация была опубликована 8 лет назад пользователемКирилл Самошин

Похожие презентации

Видео:Координаты вектора. 9 класс.Скачать

Презентация на тему: » Векторы на плоскости Работу выполнила Нина Саидзода.» — Транскрипт:

1 Векторы на плоскости Работу выполнила Нина Саидзода

2 Содержание I.ТеорияТеория II.Задачи на тему: «Векторы на плоскости» Задача 1 Задача 2 Задача 3 III.Проверь себяПроверь себя

3 Теория «Векторы на плоскости» Сложение Правило треугольника Правило параллелограмма Свойство сложения Вычитание Правило трех точек

5 А B C Для любых трех точек А, В и С справедливо равенство:

6 Правило параллелограмма А B C

8 Вычитание векторов Разностью векторов и называется такой вектор, сумма которого с вектором равна вектору

9 Вычитание B A C

10 Правило трех точек Любой вектор можно представить как разность двух векторов, проведенных из одной точки. А B K

11 Задача 1 ОТВЕТ: 3

12 Задача 2 2. Найдите длину суммы векторов и изображенных на клетчатой бумаге с размером клетки 1×1 Ответ: 5

13 Задача 3 3.Найдите длину разности векторов и, изображенных на клетчатой бумаге с размером клетки 1×1 Ответ: 4

14 Упростите выражения: а) б) в) г) Проверь себя показать

💥 Видео

ПРОСТОЙ СПОСОБ, как запомнить Векторы за 10 минут! (вы будете в шоке)Скачать

Равенство векторов, Длина вектора.Как найти длину вектора?Скачать

Разложение вектора по базису. 9 класс.Скачать

Нахождение координат вектора. Практическая часть. 9 класс.Скачать

Длина вектора через координаты. 9 класс.Скачать

Все типы 2 задание векторы ЕГЭ по математике профиль 2024Скачать