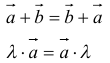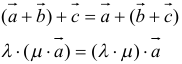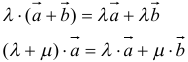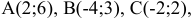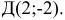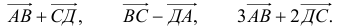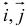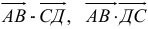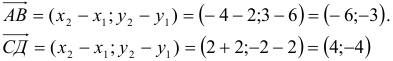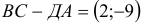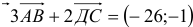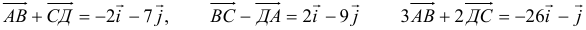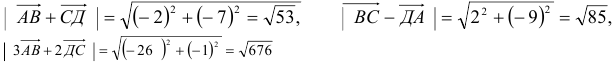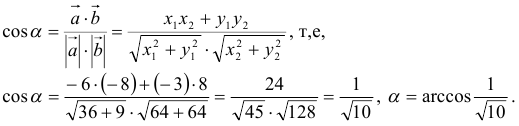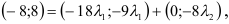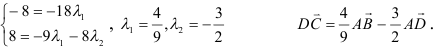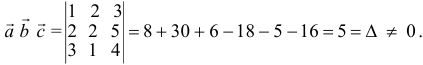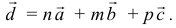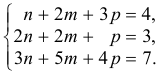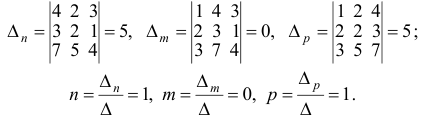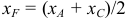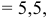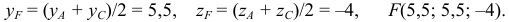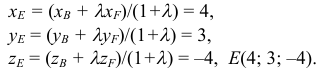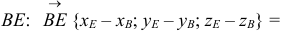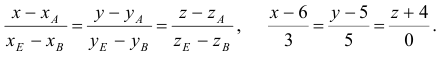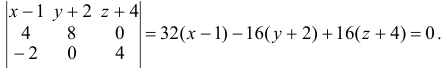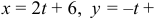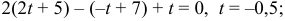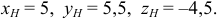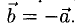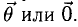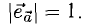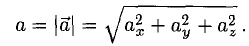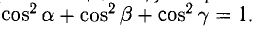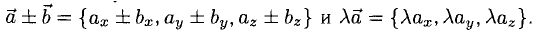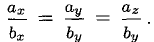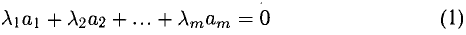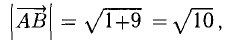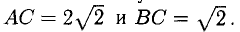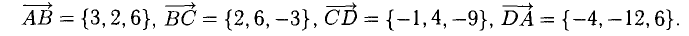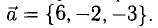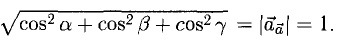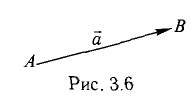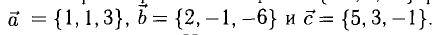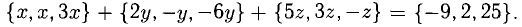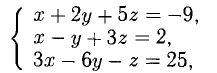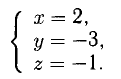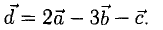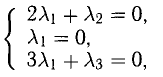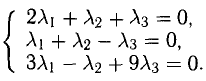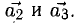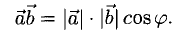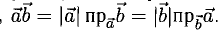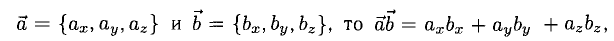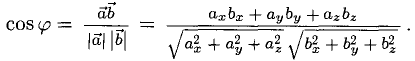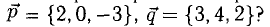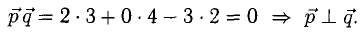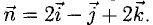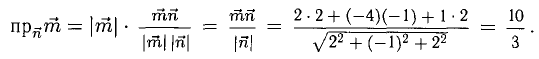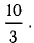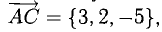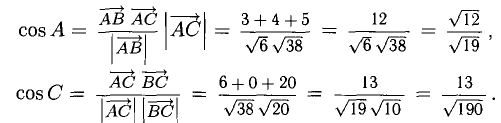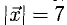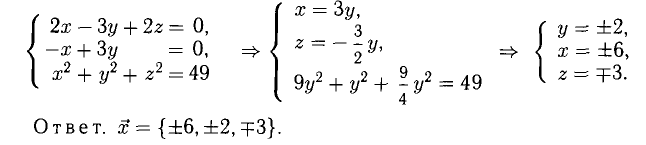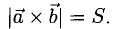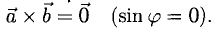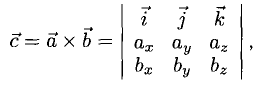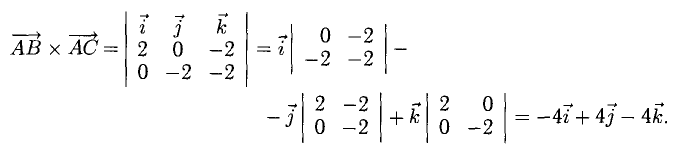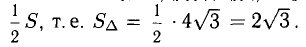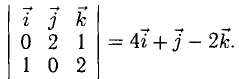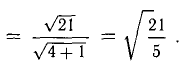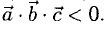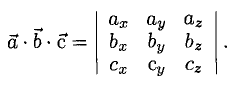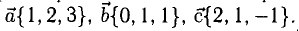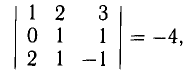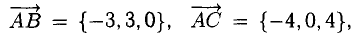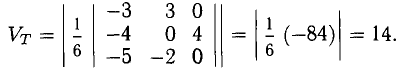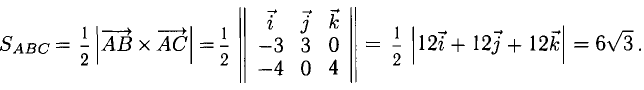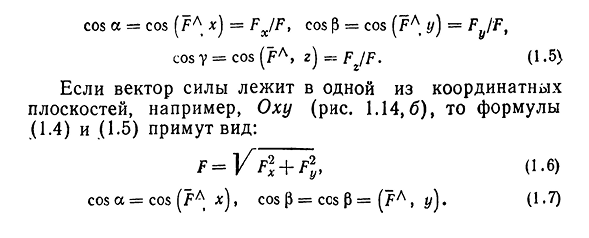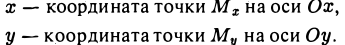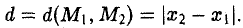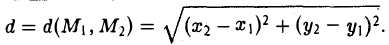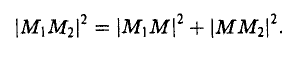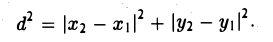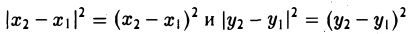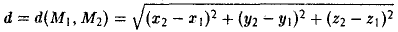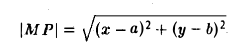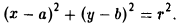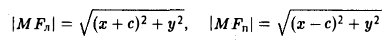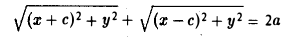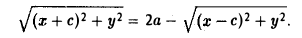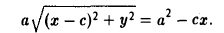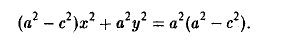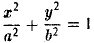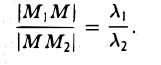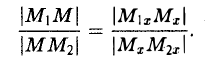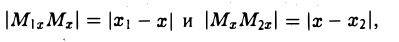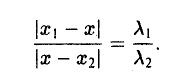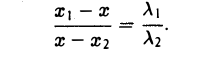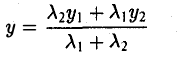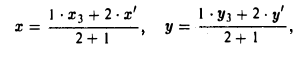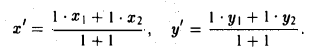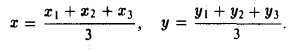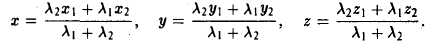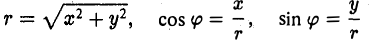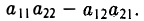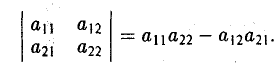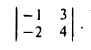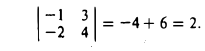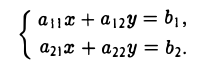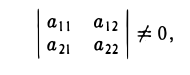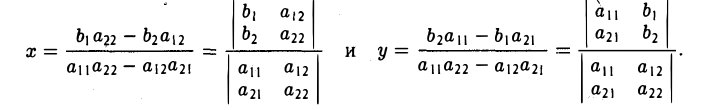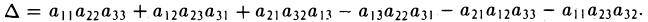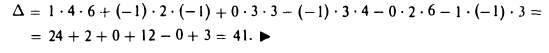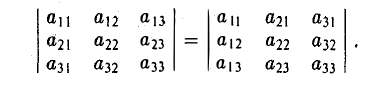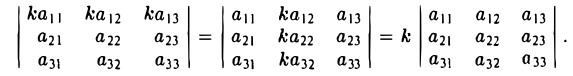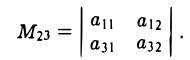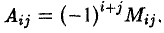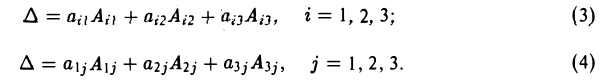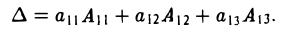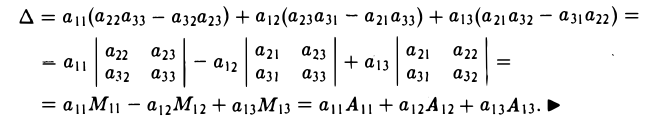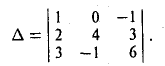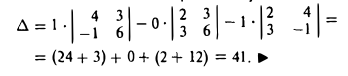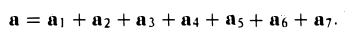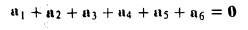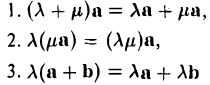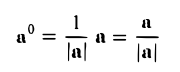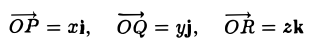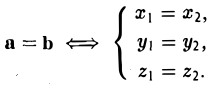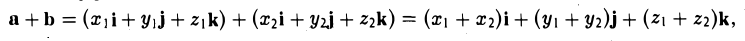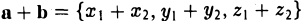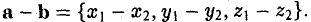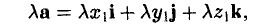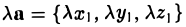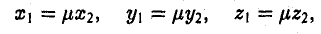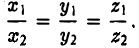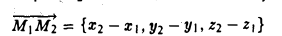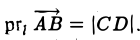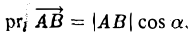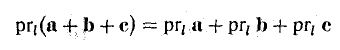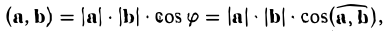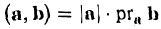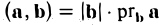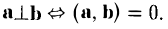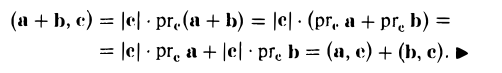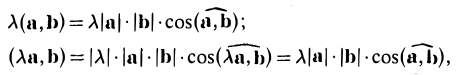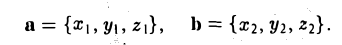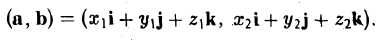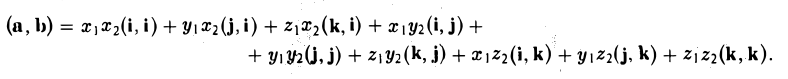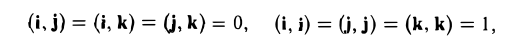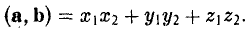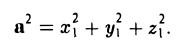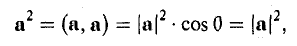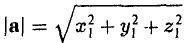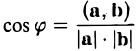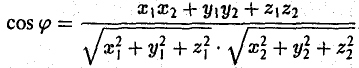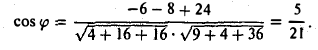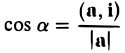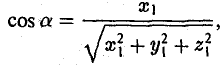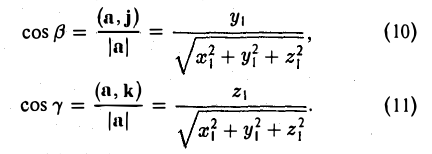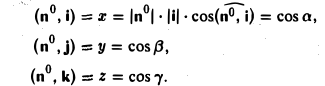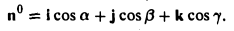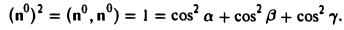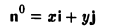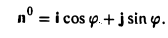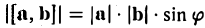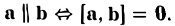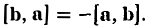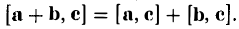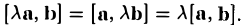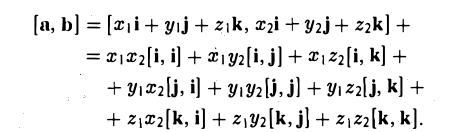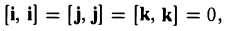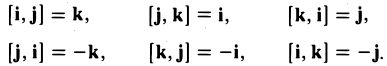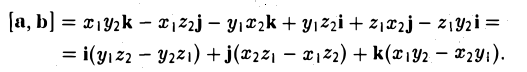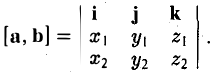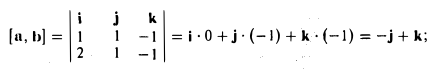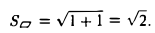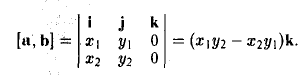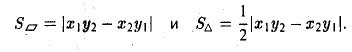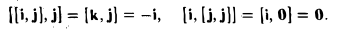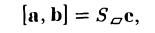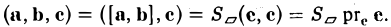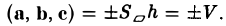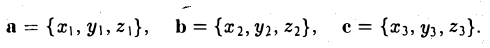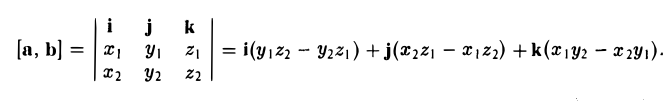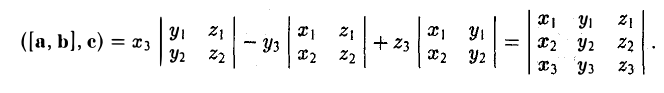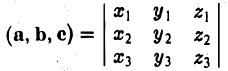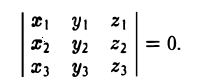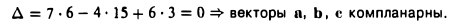Единичный вектор (орты координатных осей) — это вектор, длина которого равна единице.
i — единичный вектор оси абсцисс;
j — единичный вектор оси ординат;
k — единичный вектор оси аппликат.
i⊥j⊥k, i=j=k=1
В прямоугольной системе координат в пространстве координаты векторов равны:
i(1;0;0), j(0;1;0), k(0;0;1)
Единичные векторы являются некомпланарными.
Любой вектор можно разложить в виде вектора по ортам координатных осей, формула ниже.
a=xi+уj+zk
где x, y, z — координаты вектора проекции на соответствующие координатные оси.
Эта формула называется разложением вектора по ортам координатных осей.
Единичный вектор определяется по формуле:
Дан вектор а = (1; 2; -2)
Требуется найти длину (модуль) и единичный вектор e направления вектора а
Находим длину вектора a
затем вычисляем единичный вектор e
- Векторное произведения единичных векторов
- Единичные векторы: характеристики, как получить, примеры
- Содержание:
- Модуль, направление и смысл
- Характеристики единичного вектора
- Единичные векторы в пространстве
- Как получить / рассчитать единичный вектор?
- Произвольный вектор через единичный вектор
- Графическое представление
- Примеры единичных векторов
- Перпендикулярные единичные векторы i, j и k
- Закон Кулона
- Упражнение решено
- Решение
- Ссылки
- Векторная алгебра — основные понятия с примерами решения и образцами выполнения
- Примеры задач решаемых с применением векторной алгебры
- Векторная алгебра — решение заданий и задач по всем темам с вычислением
- Понятие вектора. Линейные операции над векторами
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Основные понятия векторной алгебры
- Прямоугольные декартовы координаты
- Координатная ось
- Прямоугольные декартовы координаты на плоскости
- Прямоугольные декартовы координаты в пространстве
- Полярные координаты
- Определители 2-го и 3-го порядков
- Понятия связанного и свободного векторов
- Линейные операции над векторами
- Сложение векторов
- Умножение вектора на число
- Координаты и компоненты вектора
- Линейные операции над векторами в координатах
- Проекция вектора на ось
- Основные свойства проекций
- Скалярное произведение векторов
- Свойства скалярного произведения
- Скалярное произведение векторов, заданных координатами
- Косинус угла между векторами. Направляющие косинусы
- Векторное произведение векторов
- Свойства векторного произведения
- Векторное произведение векторов, заданных координатами
- Смешанное произведение векторов
- Геометрический смысл смешанного произведения
- Смешанное произведение в координатах
- Двойное векторное произведение
Видео:Орт вектора. Нормировать вектор. Найти единичный векторСкачать

Векторное произведения единичных векторов
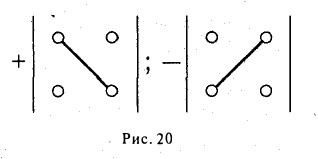
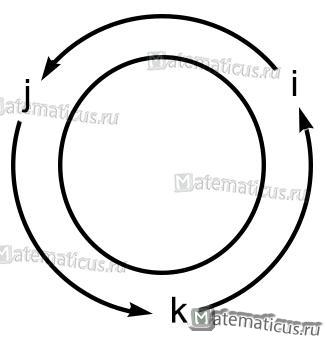
Если направление кратчайшего пути от первого вектора ко второму вектору совпадает с направлением стрелки, то произведение равно третьему вектору, а если не совпадает, то третий вектор берется со знаком «минус» . Смотрите схему 1.
На основании схемы получаем таблицу векторного произведения единичных векторов
Пример 1
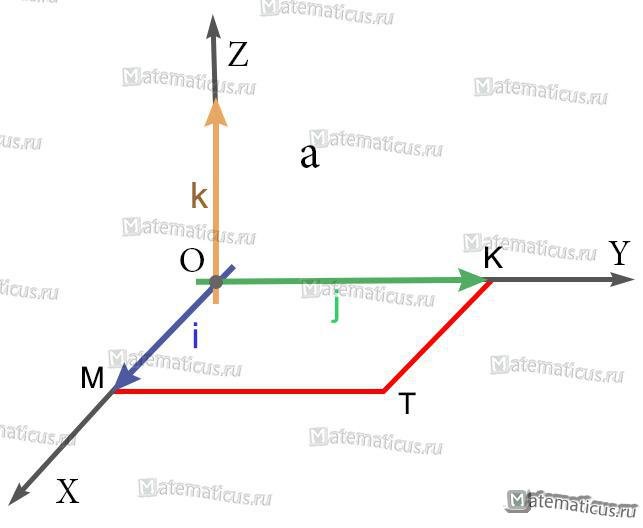
Найти векторное произведение iхj, где i, j — единичные векторы (орты) правой системы координат.
Решение
1) Так как длины основных векторов равны единице масштаба, то площадь параллелограмма MOKT численно равна единице. Значит, модуль векторного произведения равен единице.
2) Так как перпендикуляр к плоскости MOKT есть ось OZ, то искомое векторное произведение есть вектор, коллинеарный с вектором k; а так как оба они имеют модуль 1, то искомое векторное произведение равно либо k, либо -k.
3) Из этих двух возможных векторов надо выбрать первый, так как векторы i, j, k образуют правую систему (а векторы i, j, -k — левую).
iхj=k
Пример 2
Найти векторное произведение jхi.
Решение
Как в примере 1, заключаем, что вектор jхi равен либо k, либо —k. Но теперь надо выбрать -k, ибо векторы j, i, —k образуют правую систему (а векторы i, j, —k -левую).
jхi = −k
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 3.5 / 5. Количество оценок: 4
Видео:Разложение вектора по базису. 9 класс.Скачать

Единичные векторы: характеристики, как получить, примеры
Видео:Единичный векторСкачать

Содержание:
В единичные векторы — это те, модуль, величина или размер которых равны числовому значению. Единичные векторы полезны для указания направления других неединичных векторов.
Помните, что векторы — это математические объекты, которые математически представляют физические величины, зависящие от направления, такие как сила, скорость, ускорение и другие.
Независимо от физической величины, с которой они связаны, единичные векторы лишены единиц измерения, и их размер всегда равен 1, чистому числу.
Например, скорость частицы, движущейся со скоростью 3 м / с в положительном направлении декартовой оси X, обозначается: v = (3 м / с) я, где жирным шрифтом обозначены векторные величины. В этом примере модуль v составляет 3 м / с, а модуль единичного вектора я равно 1 (без единиц).
Видео:Единичные векторы Декартовой системы координатСкачать

Модуль, направление и смысл
Учитывая, насколько важно установить ориентацию этих величин для того, чтобы узнать их влияние, векторы имеют три важные характеристики: величину или модуль, связанный с размером вектора, направление и смысл. При представлении векторной величины необходимо четко указать эти аспекты.
Теперь единичный вектор может иметь любое направление и любое значение, но величина всегда должна быть равна 1.
Единичные векторы используются для обозначения конкретного направления в пространстве или на плоскости. Если, например, нам нужно работать со всеми силами, которые действуют вдоль горизонтальной оси, то единичный вектор в этом направлении помогает нам отличать эти силы от других, направленных в другом направлении.
А чтобы отличить их от неединичных векторов, в печатных буквах обычно используется жирный шрифт, а сверху ставится каретка, например:
Видео:2 37 Нахождение орта вектораСкачать

Характеристики единичного вектора
Математически единичный вектор:
Итак, мы можем установить, что:
-Модуль единичного вектора всегда равен 1, не имеет значения, является ли это силой, скоростью или другим вектором.
-Унитарные векторы имеют определенное направление, а также смысл, например единичный вектор в вертикальном направлении, который может иметь смысл вверх или вниз.
-Единичные векторы имеют точку происхождения. Когда она представлена декартовой системой координат, эта точка совпадает с началом системы: (0,0), если это плоскость, или (0,0,0), если вектор находится в трехмерном пространстве.
-Также с единичными векторами вы можете выполнять все операции сложения, вычитания и умножения векторов, которые выполняются с использованием обычных векторов. Следовательно, можно умножать единичный вектор на скаляр, а также выполнять точечное произведение и кросс-произведение.
-С помощью единичного вектора в определенном направлении могут быть выражены другие векторы, которые также ориентированы в этом направлении.
Видео:найти угол между единичными векторамиСкачать

Единичные векторы в пространстве
Чтобы выразить любой вектор в пространстве или на плоскости, можно использовать набор единичных векторов, перпендикулярных друг другу, которые образуют ортонормированный базис. Каждое из трех предпочтительных направлений пространства имеет собственный единичный вектор.
Вернемся к примеру сил, направленных по горизонтальной оси. Это ось абсцисс, которая имеет две возможности: вправо и влево. Предположим, у нас есть единичный вектор на оси x, направленный вправо, который мы можем обозначить любым из следующих способов:
Любой из них действителен. Теперь предположим, что сила F1 величиной 5 Н вдоль этой оси и направленной вправо такую силу можно выразить как:
Если бы сила была направлена вдоль оси x, но в противоположном направлении, то есть влево, то для установления этой разницы можно было бы использовать отрицательный знак.
Например, сила величиной 8 Н, расположенная по оси x и направленная влево, будет выглядеть так:
А для векторов, которые не направлены вдоль декартовых осей, также есть способ представить их в терминах ортогональных единичных векторов, используя их декартовы компоненты.
Видео:Координаты вектора. 9 класс.Скачать

Как получить / рассчитать единичный вектор?
Чтобы вычислить единичный вектор в направлении любого произвольного вектора v, применяется следующая формула:
Это модуль или величина вектора v, квадрат которого рассчитывается так:
Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Произвольный вектор через единичный вектор
В качестве альтернативы вектор v можно выразить так:
То есть произведение его модуля и соответствующего единичного вектора. Именно это и было сделано ранее, когда говорилось о силе величиной 5 Н, направленной вдоль положительной оси x.
Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Графическое представление
Графически это видно на этом изображении, где вектор v он синего цвета, а соответствующий единичный вектор в его направлении — красным.
В этом примере вектор v его величина больше, чем у единичного вектора, но объяснение справедливо, даже если это не так. Другими словами, у нас могут быть векторы, которые, например, в 0,25 раза больше единичного вектора.
Видео:Понятие вектора. Коллинеарные вектора. 9 класс.Скачать

Примеры единичных векторов
Видео:Единичные векторы и инженерная запись (видео 34) | Криволинейное движение | ФизикаСкачать

Перпендикулярные единичные векторы i, j и k
Как мы видели ранее, перпендикулярные единичные векторы я, j Y k они очень полезны для представления любого другого вектора на плоскости или в пространстве, а также для выполнения векторных операций. В терминах этих векторов произвольный вектор v представлен как:
v = vИкся + vYj + vzk
Где VИкс, vY и Vz — прямоугольные компоненты вектора v, которые являются скалярами — жирным шрифтом они не выделяются в печатном тексте.
Видео:Найдите разложение вектора по векторам (базису)Скачать

Закон Кулона
Единичные векторы часто появляются в физике. Вот, например, закон Кулона, который количественно описывает взаимодействие двух точечных электрических зарядов.
В нем говорится, что сила F Притяжение или отталкивание между указанными зарядами пропорционально их произведению, обратно пропорционально квадрату расстояния, которое их разделяет, и направлено в направлении единичного вектора, соединяющего заряды.
Этот вектор обычно представлен:
А закон Кулона в векторной форме выглядит так:
Видео:Нахождение координат вектора. Практическая часть. 9 класс.Скачать

Упражнение решено
Найдите единичный вектор в направлении вектора v = 5я + 4j -8kв условных единицах.
Видео:Векторное произведение векторов | Высшая математикаСкачать

Решение
Применяется определение единичного вектора, данное выше:
Но сначала мы должны вычислить модуль вектора, который, поскольку он состоит из трех компонентов, определяется:
|v| 2 = (5) 2 + (4) 2 + (-8) 2 = 25 + 16 + 64 = 105
Поэтому модуль v это:
Искать единичный вектор просто:
Что в конечном итоге приводит нас к следующему:
v = 0.488 я + 0.390 j – 0.781 k
Видео:Собственные векторы и собственные значения матрицыСкачать

Ссылки
- Бауэр, В. 2011. Физика для инженерии и науки. Том 1. Мак Гроу Хилл.
- Бедфорд, 2000. А. Инженерная механика: Статика. Эддисон Уэсли.
- Фигероа, Д. (2005). Серия: Физика для науки и техники. Том 1. Кинематика. Отредактировал Дуглас Фигероа (USB).
- Джамбаттиста, А. 2010. Физика. 2-й. Эд. Макгроу Хилл.
- Резник, Р. (1999). Физический. Том 1. 3-е изд. На испанском языке. Compañía Editor Continental S.A. de C.V.
История машин: от истоков до наших дней
Каковы жизненно важные функции живых существ?
Видео:11 класс, 2 урок, Координаты вектораСкачать

Векторная алгебра — основные понятия с примерами решения и образцами выполнения
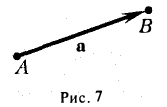
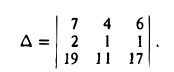
Вектором называется направленный отрезок. Вектор обозначается либо символом 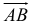
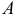
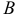

2. Длиной (модулем) вектора 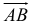
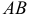
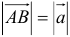
3.Вектор называется единичным, если его длина равна «1»; единичный вектор 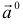


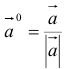
4. Вектор называется нулевым, если его начало и конец совпадают 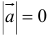
5. Векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых. Коллинеарность векторов обозначается: 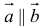

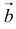
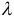
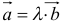
6. Два вектора называются равными, если они коллинеарны, имеют одинаковую длину и направление.
7. Вектор 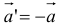

8. Векторы называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.
Для решения задач необходимо уметь выполнять линейные операции над вектором в геометрической форме, то есть над вектором, как над
направленным отрезком: сложение, вычитание векторов и умножение вектора на число.
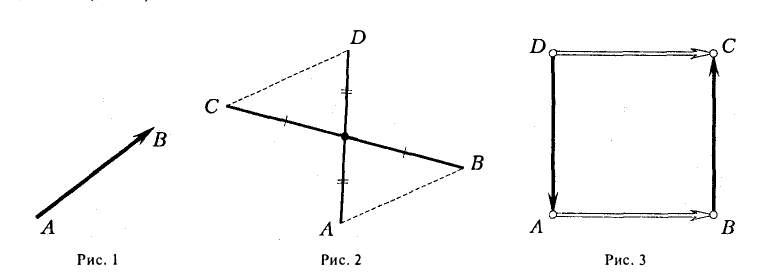
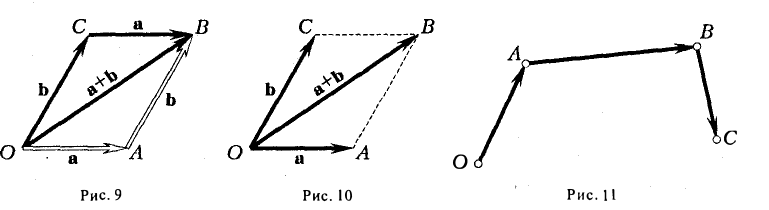
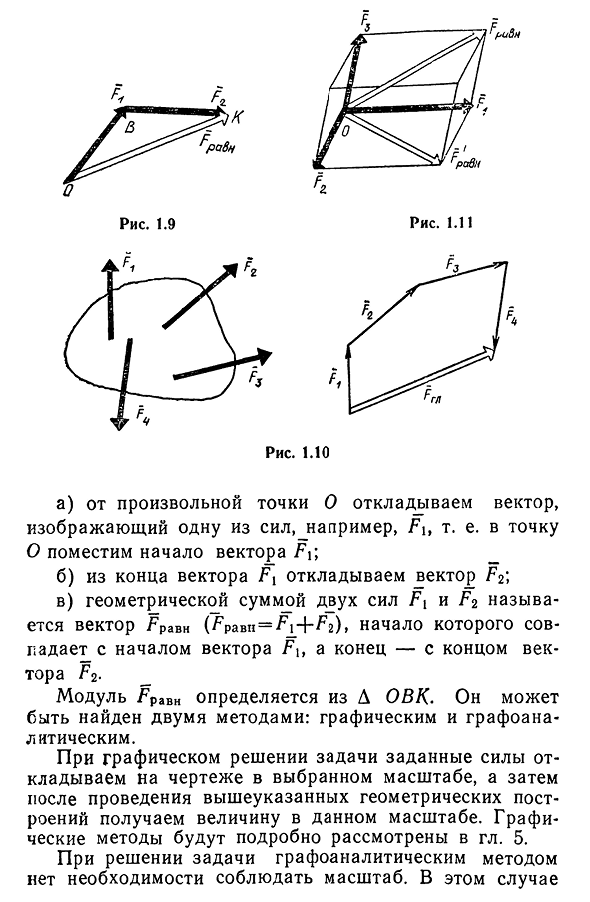
9. Сложение двух векторов можно выполнить по правилу параллелограмма (рис. 1) или по правилу треугольника (рис. 2).
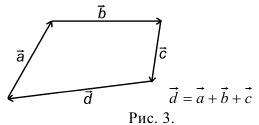
При сложении более двух векторов, лежащих в одной плоскости, используется правило «замыкающей линии многоугольника» (рис. 3).
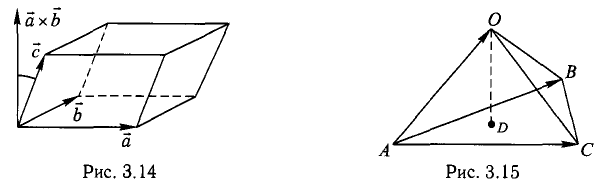
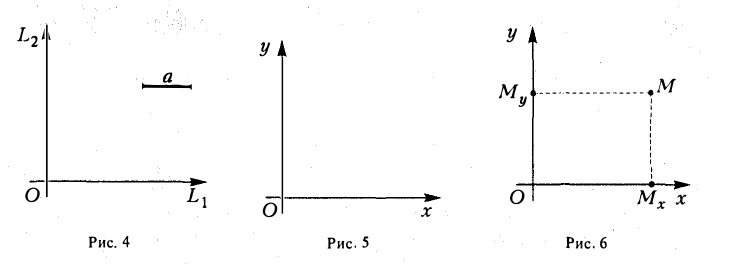
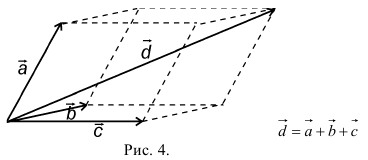
При сложении трех некомпланарных векторов удобно пользоваться правилом «параллелепипеда» (рис. 4).
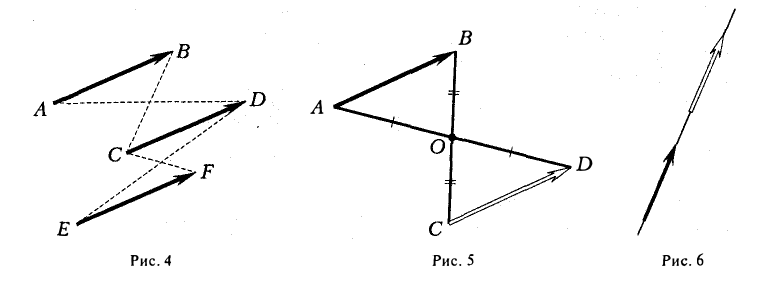
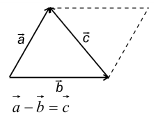
10. Действие вычитания двух векторов связано с действием сложения (рис.5).
Разностью двух векторов называется вектор, проведенный из конца вычитаемого в конец уменьшаемого. Заметим, что разностью является вектор, служащий второй диагональю параллелограмма.
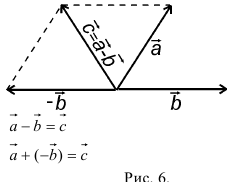
Разность можно также представить в виде сложения с противоположным вектором (рис. 6).
11. Произведением вектора 
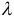
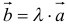
- модуль, равный
;
- направление, одинаковое с
, если
.
- направление, противоположное с
, если
.
12. Для решения задач полезно знать также следующие законы и свойства:
- переместительный:
- сочетательный:
- распределительный:
Видео:СКАЛЯРНОЕ УМНОЖЕНИЕ ВЕКТОРОВ ЧАСТЬ I #математика #егэ #огэ #формулы #профильныйегэ #векторыСкачать

Примеры задач решаемых с применением векторной алгебры
Задача:
Пусть даны точки
1) Найти координаты векторов
2) Написать разложение этих векторов по базису
3) Найти длины этих векторов
4) Найти скалярное произведение
5) Найти угол между векторами 

6) Найти разложение вектора 

Решение:
1) Вычислим координаты векторов 
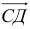
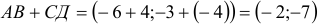
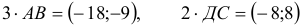
2)
4) Для вычисления угла между векторами воспользуемся формулой:
5) Разложить вектор 

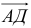


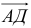
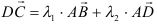
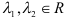
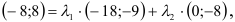
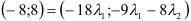
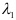
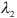
Задача:
а). Даны векторы 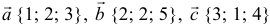
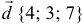
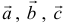
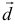
Решение:
Три вектора образуют базис, если 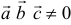
Найдем координаты вектора 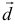
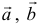
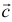
Два вектора равны, если их соответствующие координаты равны.
Решим систему методом Крамера:
Ответ: 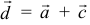
Задача:
Даны координаты вершин тетраэдра 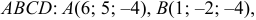
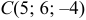
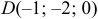
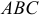

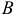
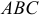


Решение:
1) Найдем координаты т. 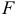
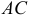
Точка 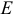
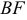
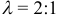
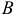
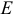
2) Найдем направляющий вектор прямой 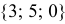

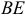
3) Найдем уравнение плоскости 
Найдем каноническое уравнение прямой, перпендикулярной плоскости 

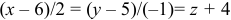
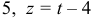
Найдем координаты точки 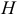

Координаты точки 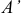


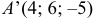
Ответ: 1) координаты точки пересечения медиан 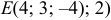
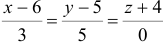
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Возможно вам будут полезны эти страницы:
Видео:Координаты вектора, перпендикулярного векторамСкачать

Векторная алгебра — решение заданий и задач по всем темам с вычислением
Понятие вектора. Линейные операции над векторами
1°. Любые две точки 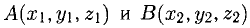
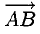
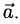
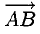
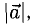
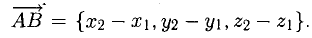
Векторы, расположенные на одной прямой или на параллельных прямых, называются коллинеарными.
Два вектора 
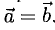
Векторы 
Вектор называется нулевым, если его модуль равен нулю, и обозначается
2°. Линейными называются действия сложения, вычитания векторов и умножения вектора на число.
1.Если начало 

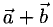


2.Если начала векторов 




3.При умножении вектора 
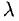
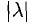
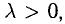
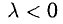
Вектор 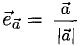

3°. Запись ci — 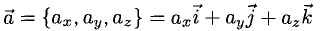

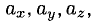

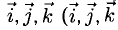
4°. Числа 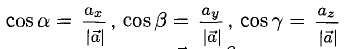
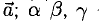

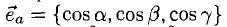

5°. Линейные операции над векторами, которые заданы своими координатами, определяются так: пусть 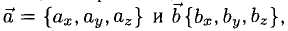
Следовательно, при сложении векторов складываются их соответствующие координаты, а при умножении вектора на число умножаются на число все координаты вектора.
6°. Необходимое и достаточное условие коллинеарности векторов 
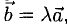
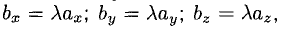
Если один из членов какого-нибудь из этих отношений равен нулю, то и второй член того же отношения должен быть нулем. Геометрически это значит, что в этом случае оба вектора перпендикулярны соответствующей координатной оси (например, если 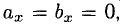
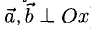
7°. Система векторов 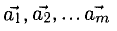
( 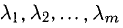

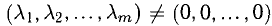
Примеры с решениями
Пример:
Доказать, что треугольник с вершинами в точках A(1,2), B(2,5), С(3,4) прямоугольный.
Решение:
Построим векторы, совпадающие со сторонами треугольника (см. п. 1°): 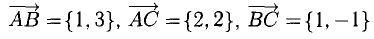
Найдем длины сторон: 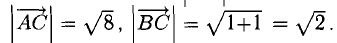
Нетрудно видеть, что 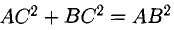
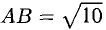
Пример:
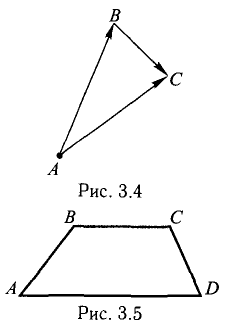
Проверить, что точки А( 2,-4,3), В(5, —2,9), С( 7,4,6) и D(6,8, -3) являются вершинами трапеции.
Решение:
Составим векторы-стороны с целью обнаружения коллинеарности векторов (в трапеции ВС || AD) (рис. 3.5):
Имеем 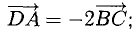
Пример:
Найти орт и направляющие косинусы вектора
Решение:
Имеем 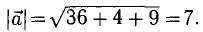
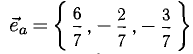
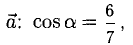
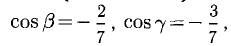
Пример:
Определить точку В, которая является концом вектора 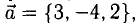
Решение:
Пусть точка В имеет координаты B(x,y,z) (рис. 3.6). Тогда координа- ^ ты вектора (п. 1°)
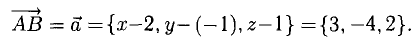
Следовательно, 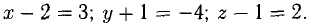
Пример:
Вектор 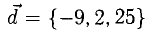
Решение:
Необходимо найти такие числа х, у, z, что 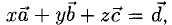
Имея в виду, что при сложении векторов складываются их координаты и равные векторы имеют равные координаты, приходим к системе уравнений
Ответ.
Пример:
Показать, что система векторов 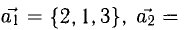
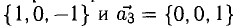
Решение:
В данном случае равенство (1) имеет вид 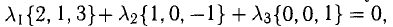
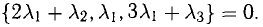
из которой следует, что 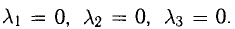
Пример:
Показать, что система векторов 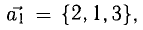
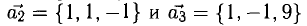
Решение:
Равенство (1) равносильно системе уравнений
Она имеет ненулевое решение, например, 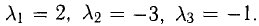
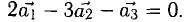
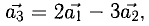
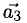
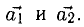
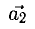
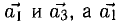
Скалярное произведение векторов
1°. Скалярным произведением двух ненулевых векторов а и b называется число, равное произведению их длин на косинус угла 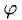
Из 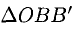
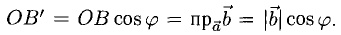
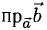


Итак,
т.е. скалярное произведение векторов равно сумме произведений одноименных координат этих векторов.
При этом 
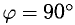
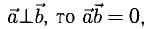
3°. Из определения скалярного произведения следует формула для вычисления угла между двумя векторами:
Примеры с решениями
Пример:
Перпендикулярны ли векторы 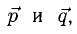
Решение:
Условие перпендикулярности векторов (п. 2°) 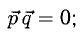
Пример:
Найти проекцию вектора 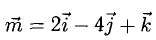
Решение:
Имеем 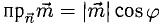
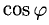
Ответ
Пример:
Зная векторы, совпадающие с двумя сторонами: 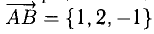
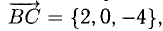
Решение:
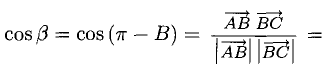
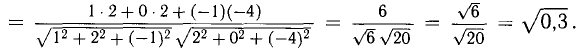
При помощи таблиц находим 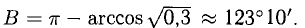
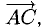
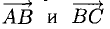
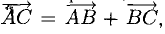
Ответ. 123° 10′, 19°29′, 37°21′.
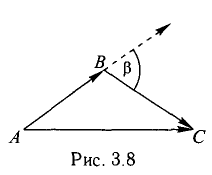
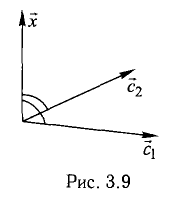
Пример:
Найти координаты вектора 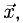
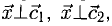
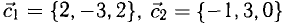
Решение:
На рис. 3.9 имеем 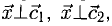
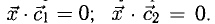
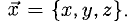
Векторное произведение векторов
1°. Векторы 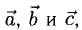

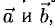
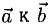
2°. Векторным произведением ненулевых векторов 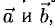

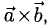
1) 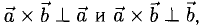
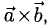
2) Вектор 
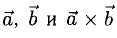
3) 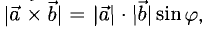
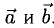
Если векторы 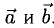

3°. Если известны координаты векторов-сомножителей 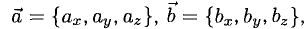
в которой определитель следует разложить по элементам первой строки.
Примеры с решениями
Пример:
Найти площадь треугольника, вершины которого находятся в точках А(1,2,3), В<3,2,1), С(1,0,1).
Решение:
Найдем координаты векторов 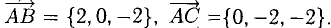
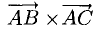
Найдем длину этого вектора, которая равна численно площади параллелограмма S (п. 2°): 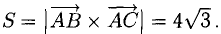
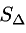
Пример:
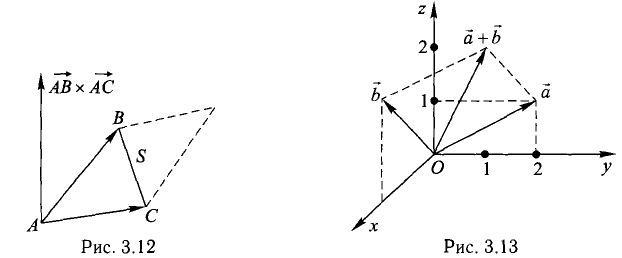
Построить параллелограмм на векторах 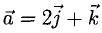
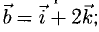

Сделаем чертеж (рис. 3.13). Имеем 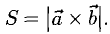
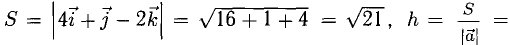
Смешанное произведение векторов
1°. Смешанным произведением трех ненулевых векторов 


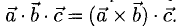

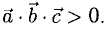

Модуль смешанного произведения векторов 
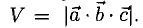
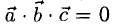

Объем тетраэдра с вершинами в точках 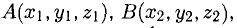
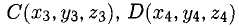
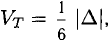
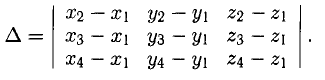
2°. Условие 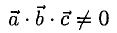

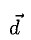
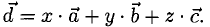
Примеры с решениями
Пример:
Найти объем параллелепипеда, построенного на векторах
Решение:
Искомый объем 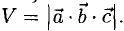
Пример:
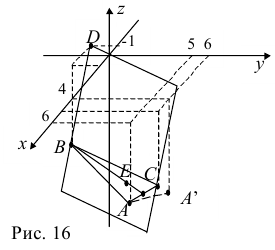
В точках 0(0,0,0), А(5,2,0), В(2,5,0) и С(1,2,4) находятся вершины пирамиды. Вычислить ее объем, площадь грани ABC и высоту пирамиды, опущенную на эту грань.
Решение:
1) Сделаем схематический чертеж (рис. 3.15).
2) Введем векторы 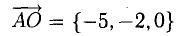
3) Площадь грани ABC
4) Объем пирамиды 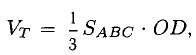
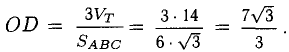
Ответ.
Видео:Координаты вектора в пространстве. 11 класс.Скачать

Основные понятия векторной алгебры




Видео:#вектор Разложение вектора по ортам. Направляющие косинусыСкачать

Прямоугольные декартовы координаты
Координатная ось
Пусть на плоскости или в пространстве задана произвольная прямая L: Ясно, что по этой прямой L сы можем перемещаться в oднoм из двух противоположных направлений. Выбор любого (одного) из этих направлений будем называть ориентацией прямой L.
Оnределение:
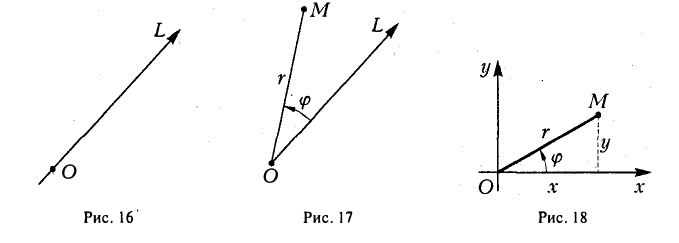
Прямая с заданной на ней ориентацией называется осью. На чертеже ориентация оси указывается стрелкой (рис. 1 ) . Фиксируем на оси 
Пусть М — произвольная точка оси 
Оnределение:
Ось 
Прямоугольные декартовы координаты на плоскости
Пусть П — произвольная плоскость. Возьмем на ней некоторую точку О и проведем через эту точку взаимно перпендикулярные прямые L 1 и L 2. Зададим на каждой из nрямых L 1 и L 2 ориентацию и выберем единый масштабный отрезок а. Тогда эти прямые nревратятся в координатные оси с общей точкой отсчета О (рис. 4).
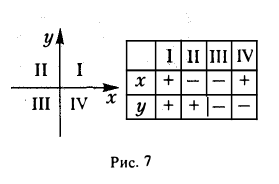
Назовем одну из координатных осей осью абсцисс (осью Ох), друrую —осью ординат (осью Оу) (рис. 5). Точка О называется началом координат. Пусть М — произвольная точка плоскости П (рис. 6). Проведем через точку М прямые, перпендикулярные координатным осям, и поставим ей в соответствие упорядоченную пару чисел (х, у) по следующему nравилу:
Числа х и у называются прямоугольными декартовыми при этом х называется ее абсциссой, а у — ординатой. координатами точки М; Обозначение: М(х, у). Чтобы кратко охарактеризовать описанную конструкцию, говорят, что на плоскости П задана прямоугольная декартова система координат Ох у. Координатные оси разбивают плоскость на четыре части, называемые четвертями или квадрантами. На рисунке и в таблице показано, как эти квадранты нумеруются (рис. 7).
Замечание:
Масштабные от резки на координатных осях могут быть и разной длины. В этом случае координатная система называется просто прямоугольной.
Прямоугольные декартовы координаты в пространстве
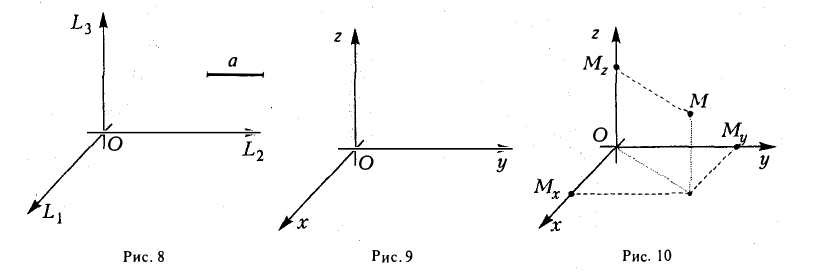
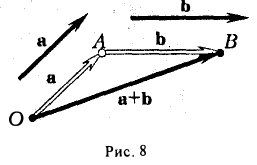
Возьмем в пространстве некоторую точку О и проведем через нее три взаимно перпендикулярные прямые L 1 , L 2 и L 3 . Выберем на каждой из nрямых ориентацию и единый масштаб. Прямые L 1 , L 2 и L 3 превратятся в координатные оси с общей точкой отсчета О (рис. 8).
Назовем одну из этих осей осью абсцисс (осью Ох), вторую — осью ординат (осью Оу) и третью — осью аппликат (осью Oz) (рис. 9). Точка О называется началом координат. Пусть М — nроизвольная точка (рис. 10). Проведем через точку М nлоскости, перпендикулярные координатным осям, и поставим ей в соответстnие упорядоченную тройку чисел (х, у, z) по следующему правилу:
Числа х, у и z называются прямоугольными декартовыми координатами точки М; при этом х называется абсциссой точки М, у — ее ординатой, а z —аппликатой. Обозначение: М(х, у, z). Таким образом, в пространстве введена прямоугольная декартова система координат.
Оnределение:
Плоскость, проходящая через любую пару координатных осей, называется координатной плоскостью.
Координатных плоскостей три: Оху, Oyz и Oxz. Эти плоскости разбивают пространство на восемь частей — октантов. 1 .4. Простейшие задачи аналитической геометрии А. Расстояние между точками Пусть М 1 (х 1 ) и М 2 (х 2 )- две точки на координатной оси. Тогда расстояние d между ними вычисляется по формуле
Если на плоскости задана прямоугольная декартова система координат Оху, то расстояние d между любыми двумя точками М 1 (х 1 , у1 и М2 (х2 , y2) вычисляется по следующей формуле
Рассмотрим прямоугольный треугольник ∆MM1M2 (pиc. l l). По теореме Пифагора
,и извлекая из обеих частей равенства квадратный корень, приходим к требуемой формуле .
Замечание:
Расстояние между точками 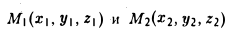
Задача:
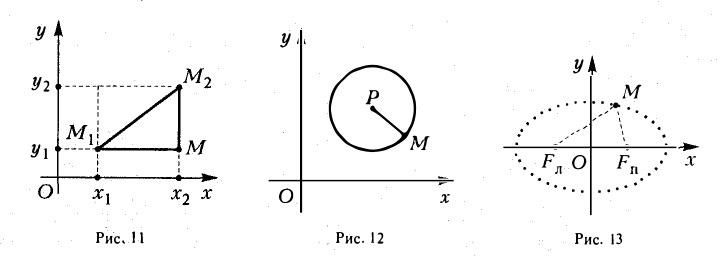
Написать уравнение окружности радиуса т с центром в точке Р(а, b).
Пусть М(х, у) — точка окружности (рис. 12). Это означает, что |M P| = r. Заменим |M P|его выражением
и возведем обе части полученного равенства в квадрат:
Это есть каноническое уравнение окружности радиуса r с центром в точке Р(а, b) .
Задача:
Пусть F л (-с, 0) и F n (c, 0) -фиксированные точки плоскости, а -заданное число (а > с ≥ 0). Найти условие, которому удовлетворяют координаты х и у точки М, обладающей следующим свойством: сумма расстояний от точки М до Fл и до F n равна 2а.
Вычислим расстояния между точками М и F л и между точками М и F n . Имеем
Перенесем второй корень в правую часть
Возводя обе части в квадрат, после простых преобразований получим
С целью дальнейших упрощений вновь возводим обе части в квадрат. В результате nриходим к равенству
Полагая b 2 = а 2 — с 2 и деля обе части nоследнего соотноwения на а 2 b 2 , nолучаем уравнение эллипса
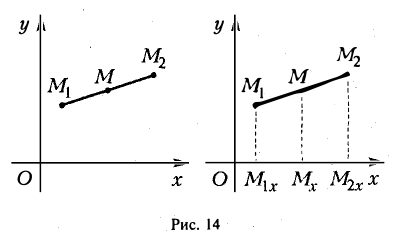
Деление отрезка в данном отношении:
Требуется выразить координаты х и у этой точки через координаты концов отрезка М1М2 и числа λ 1 и λ 2 . Предположим сначала, что отрезок М1М2 не параллелен оси ординат Оу (рис. 14). Тогда
то из последних двух соотношений получаем, что
Точка М лежит между точками М1 и М2 , поэтому либо х 1 х > х 2 . В любом из этих случаев разности х1 — х и х — х 2 имеют одинаковые знаки. Это позволяет переписать последнее равенство в следующей форме
В случае, когда отрезок М1М2 параллелен оси Оу, х 1 = х 2 = х. Заметим, что тот же результат дает формула (*), если nоложить в ней х 1 = х 2 . Справедливость формулы
доказывается аналогичным рассуждением .
Задача:
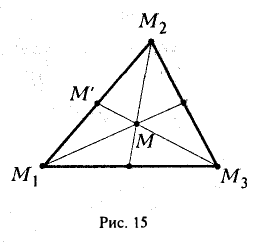
Найти координаты центра тяжести М треугольника с вершинами в точках . М1 ( х 1 , у 1 ), М2 ( х 2 , у 2 ) и М3 ( х 3 , у 3 ). Восnользуемся тем, что центр тяжести треугольника совпадает с точкой пересечения его медиан. Точка М делит каждую медиану в отношении 2 : 1, считая от вершины (рис. 15). Тем самым, ее координаты х и у можно найти по формулам
где х’ и у’ — координаты второго конца М’ медианы М3 М’. Так как М’ — середина отрезка М1М2, то
Полученные соотношения позволяют выразить координаты z и у центра тяжести М треугольника ∆М1М2М3 через координаты его вершин:
Замечание:
Полярные координаты
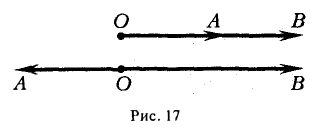
Предположим, что задана точка О, ось 
Пусть М — произвольная точка плоскости, отличная от точки О (рис.17). Ее положение на плоскости однозначно определяется двумя числами: расстоянием г между точками О и М и отсчитываемым против часовой стрелки углом φ между положительным лучом оси 
Точка О называется полюсом, 
Ясно, что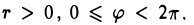
Таким образом, на плоскости можно задать еще одну координатную систему — полярную.
Прямоугольную декартову систему координат Оху будем называть согласованной с заданной полярной, если начало координат 0(0, 0) — полюс, ось Ох — полярная ось, а ось Оу составляете осью Ох угол, равный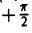
(рис.18). В свою очередь
Пример:
Пусть R > О — заданное число. Множество точек плоскости, полярные координаты (г,
Определители 2-го и 3-го порядков
Определителем второго порядка называется число
Обозначение:
Тем самым, для вычисления определителя второго порядка нужно из произведения а11, а22 элементов главной диагонали вычесть произведение а12, а21 элементов его побочной диагонали (рис. 20).
Пример:
По правилу (1) имеем
С определителями второго порядка мы встречаемся уже при отыскании решения системы двух линейных алгебраических уравнений с двумя неизвестными
Решая эту систему методом исключения неизвестных при условии, что
Пусгь теперь даны девять чисел aij (i = I, 2, 3; j = I, 2, 3).
Определителем третьего порядка называется число, обозначаемое символом
и вычисляемое по следующему правилу:
Первый индекс i элемента aij указывает номер строки, в которой он расположен, а второй индекс j — номер столбца.
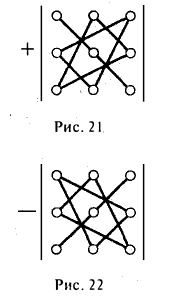
Чтобы разобраться с распределением знаков в правой части формулы (2), обратим внимание на следующее: произведение элементов а11, а22, а33 главной диагонали входит в формулу со своим знаком, также как и произведение а11, а22, а33 и а11, а22, а33 элементов, расположенных в вершинах треугольников, основания которых параллельны главной диагонали (рис. 21); с другой стороны, произведение а13, а22, а31 элементов побочной диагонали, а также произведения а12, а21, а33 и а11, а23, а32 — с противоположным знаком (рис.22). Такой подход к вычислению определителя третьего порядка называется правилом треугольника.
Пример:
Применяя правило треугольника, находим
Установим некоторые свойства определителей 3-го порядка, легко проверяемые при помощи разложений (1) и (2).
Свойство:
Величина определителя не изменится, если все его строки заменить его столбцами с теми же номерами
Свойство:
При перестановке любых двух строк (или любых двух столбцов) определителя он изменяет свой знак на противоположный.
Свойство:
Общий множитель всех элементов одной строки (или одного столбца) определителя можно вынести за знак определителя
Следующие три свойства определителя вытекают из свойств 1-3. Впрочем, в их справедливости можно убедиться и непосредственно, пользуясь формулами (1) и (2).
Свойство:
Если определитель имеет две равные строки (или дна равных столбца), то он равен нулю.
Свойство:
Если все элементы некоторой строки (или некоторого столбца) равны нулю, то и сам определитель равен нулю.
Свойство:
Если соответствующие элементы двух строк (или двух столбцов) пропорциональны, то определитель равен нулю.
Укажем еще один способ вычисления определителя 3-го порядка
Минором Mij элемента aij определителя ∆ называется определитель, получаемый изданного путем вычеркивания элементов i-й строки и j-ro столбца, на пересечении которых находится этот элемент. Например, минором элемента a23 будет определитель
Алгебраическим дополнением элемента Aij называется минор Mij — этого элемента, взятый со своим знаком, если сумма i + j номеров строки и столбца, на пересечении которых расположен элемент aij, есть число четное, и с противоположным знаком, если это число нечетное:
Теорема:
Определитель равен сумме произведений элементов любой его строки (любого его столбца) на их алгебраические дополнения, так что имеют место следующие равенства
Покажем, например, что
Пользуясь формулой (2), получаем, что
Правило (3) называется разложением определителя по элементам i-й строки, а правило (4) — разложением определителя по элементам j -го столбца.
Пример:
Раскладывая определитель по элементам 1-ой строки, получим
Понятия связанного и свободного векторов
Рассмотрим две точки А и В. По соединяющему их отрезку можно перемещаться в любом из двух противоположных направлений. Если считать, например, точку А начальной, а точку В конечной, то тогда получаем направленный отрезок АВ, в другом случае — направленный отрезок В А. Направленные отрезки часто называют связанными или закрепленными векторами. На чертеже заданное направление указывается стрелкой (рис. 1).
В случае, когда начальная и конечная точки совпадают, А = В, связанный вектор называется нулевым.
Определение:
Будем говорить, что связанные векторы АВ и CD равны, если середины отрезков AD и ВС совпадают (рис. 2).
Обозначение:
Заметим, что в случае, когда точки А, В, С и D не лежат на одной прямой, это равносильно тому, что четырехугольник ABCD — параллелограмм. Ясно, что равные связанные векторы имеют равные длины.
Пример:
Рассмотрим квадрат и выберем векторы, как указано на рис.3. Векторы АВ и DC равны, а векторы ВС и DA не равны.
Укажем некоторые свойства равных связанных векторов:
- Каждый связанный вектор равен самому себе: АВ = АВ.
- Если АВ = CD, той CD = АВ.
- Если АВ = CD и CD = EF,то АВ = EF (рис.4).
Пусть АВ — заданный связанный вектор и С — произвольная точка. Ясно, что, опираясь на определение, всегда можно построить точку D так, чтобы
CD = АВ.
Тем самым, от каждой точки можно отложить связанный вектор, равный исходному (рис. 5).
Мы будем рассматривать свободные векторы, т. е. такие векторы, начальную точку которых можно выбирать произвольно, или, что то же самое, которые можно произвольно переносить параллельно самим себе. Ясно, что свободный вектор 
Если в качестве начальных выбирать лишь те точки, которые лежат на прямой, определяемой заданным (ненулевым) связанным вектором, то мы приходим к понятию скользящего вектора (рис. 6).
Связанные и скользящие векторы широко используются в теоретической механике.
Для обозначен ия свободных векторов будем пользоваться полужирными строчными латинскими буквами — а, b, с,… ; нулевой вектор обозначается через 0.
Пусть заданы вектор а и точка А. Существует ровно одна точка В, для которой

(рис.7). Операция построения связанного вектора АВ, для которого выполняется это равенство, называется откладыванием свободного вектора а от точки А.
Заметим, что связанные векторы, получаемые в результате описанной операции откладывания, равны между собой и, значит, имеют одинаковую дли ну. Это позволяет ввести длину свободного вектора а, которую мы будем обозначать символом |а. Длина нулевого вектора равна нулю. Если а = b, то |а| = |b; обратное неверно.
Линейные операции над векторами
Сложение векторов
Пусть заданы два вектора а и b. Возьмем какую-нибудь точку О и отложим от нее вектор a: 


Нетрудно заметить, что сложение векторов коммутативно, т. е. для любых векторов а и b справедливо равенство
а + b = b + а
Если отложить векторы а и 1» от обшей точки О и построить на них как на сторонах параллелограмм, то вектор 
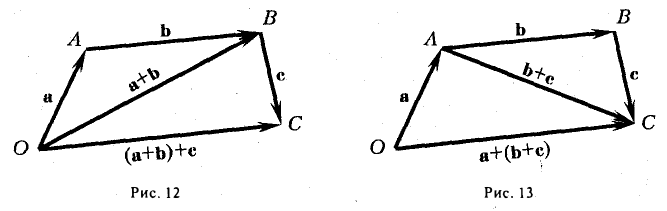
Пусть заданы три вектора, например, a, b и с. Отложим от произвольной точки О вектор a: 

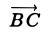

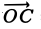
(а +b) + с = а + (b + с),
т. е. сложение векторов ассоциативно. Опуская скобки, можно говорить о сумме трех векторов и записывать ее так:
а + b + с.
Аналогично определяется сумма любого числа векторов: это есть вектор, который замыкает ломаную, построенную из заданных векторов. На рис. 14 показан», как построить сумму семи векторов:
Приведенный способ сложения произвольного числа векторов называется правилом замыкающего ломаную.
Пример:
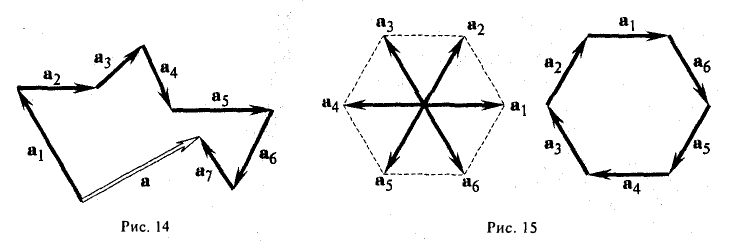
Найти сумму векторов, идущих из центра правильного шестиугольника в его вершины.
По правилу замыкающего ломаную получаем
Умножение вектора на число
Определение:
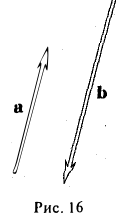
Свободные векторы а и b называются коллинеарными, если определяющие их связанные векторы лежат на параллельных или на совпадающих прямых (рис. 16).
Обозначение: а||b.
Замечание:
Из определения следует, что если хотя бы один из векторов a и b нулевой, то они коллинеарны.
Если отложить коллинеарные векторы а и b от обшей точки О, 

Если векторы имеют равные длины и одинаково направлены, то они равны. Пусть а — вектор, λ — вещественное число.
Определение:
Произведением вектора а на число λ называется вектор b такой, что
2) векторы а и b одинаково (соответственно, противоположно) направлены, если λ > 0 (соответственно, λ
(здесь λ и μ — любые действительные числа, а и Ь — произвольные векторы).
Определение:
Вектор, длина которого равна единице, называется единичным вектором, или ортом, и обозначается а° (читается: а с нуликом), |а°| = 1.
Если а ≠ 0, то вектор
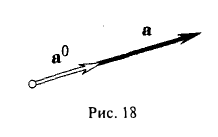
есть единичный вектор (орт) направления вектора а (рис. 18).
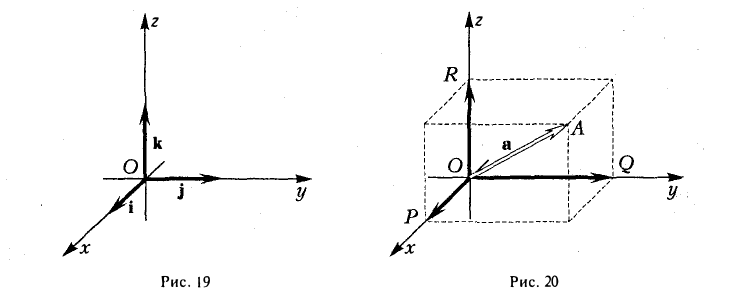
Координаты и компоненты вектора
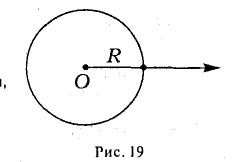
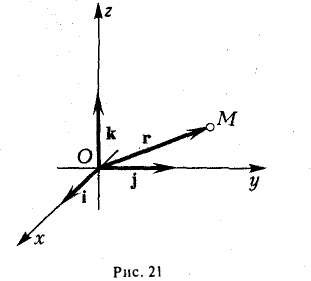
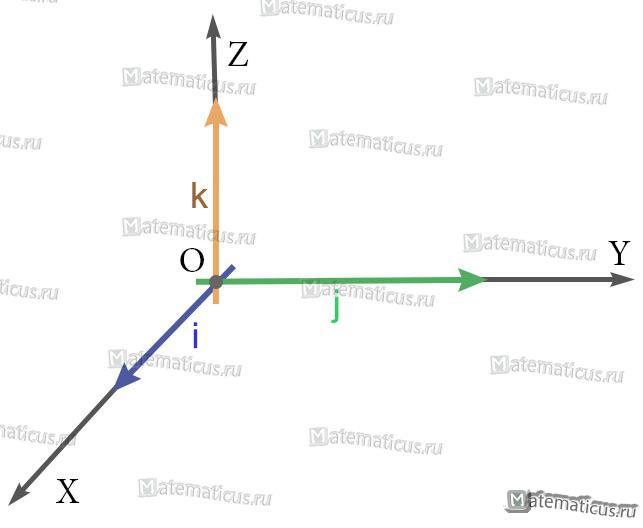
Выберем в пространстве прямоугольную декартову систему координат. Обозначим через i, j, к единичные векторы (орты) положительных направлений осей Ox, Оу, Oz (рис. 19). Рассмотрим произвольный вектор п, начало которого лежит в начале координат О, а конец — в точке А. Проведем через точку А плоскости, перпендикулярные осям Ох, Оу и Oz. Эти плоскости пересекут координатные оси в точках Р, Q и R соответственно. Из рис. 20 видно, что
Векторы 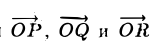
поэтому найдутся числа х, у, z такие, что
а = xi + yj + zk. (2)
Формула (2) называется разложением вектора а по векторам i, j, к. Указанным способом всякий вектор может быть разложен по векторам i, j, k.
Векторы i, j, к попарно ортогональны, и их длины равны единице. Тройку i, j, k называют ортонормированным (координатным) базисом (ортобазисом).
Можно показать, что для каждого вектора а разложение (2) по базису i, j, к единственно, т. е. коэффициенты х, у, z в разложении вектора а по векторам i, j, к определены однозначно. Эти коэффициенты называются координатами вектора а. Они совпадают с координатами х, у, z точки А — конца вектора а. Мы пишем в этом случае
а = .
Эта запись означает, что свободный вектор а однозначно задастся упорядоченной тройкой своих координат. Векторы xi, yj, zk, сумма которых равна вектору а, называются компонентами вектора а.
Из вышеизложенного следует, что два вектора а = < х1, у1, z1 > и b = <х2, у2, z2> равны тогда и только тогда, когда соответственно равны их координаты, т. е.
Радиус-вектором точки М(х,у, z) называется вектор г = xi + yj + zk, идущий из начала координат О в точку М (рис. 21).
Линейные операции над векторами в координатах
— при сложении векторов их координаты попарно складываются. Аналогично получаем
— при умножении вектора на число все его координаты умножаются на это число.
Пусть а = < х1, у1, z1>, b = < х2, у2, z2 > — коллинеарные векторы, причем b ≠ 0. Тогда а = μb, т.е.
Обратно, если выполняются соотношения (3), то а = μb, т. е. векторы a и b коллинеарны.
Таким образом, векторы а и b коллинеарны тогда и только тогда, когда их координаты пропорциональны.
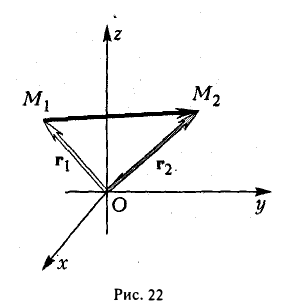
Пример:
Найти координаты вектора 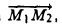
Из рис. 22 видно, что 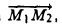
— координаты вектора ММг равны разностям одноименных координат конечной М2 и начальной М точек этого вектора.
Проекция вектора на ось
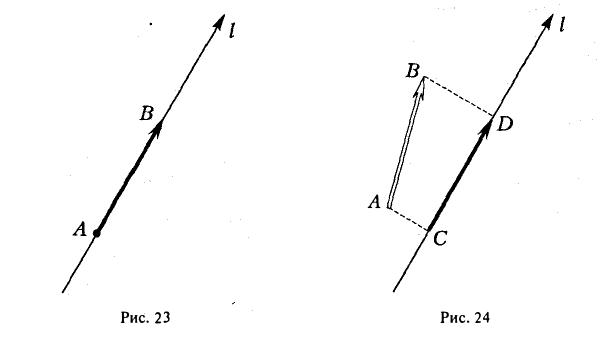
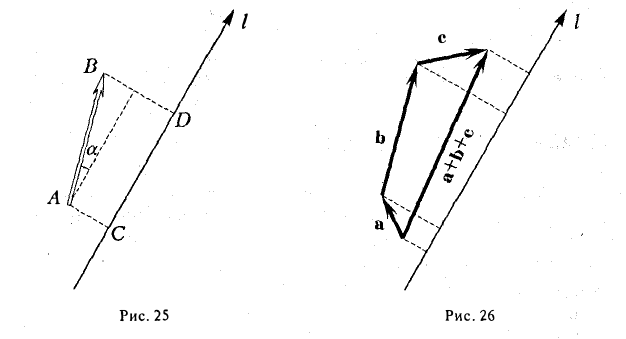
Рассмотрим на оси l ненулевой направленный отрезок АВ (рис.23). Величиной направленного отрезка АВ на оси l называется число, равное длине отрезка АВ, взятой со знаком «+», если направление отрезка АВ совпадаете направлением оси l, и со знаком «-», если эти направления противоположны.
Рассмотрим теперь произвольный вектор 
Определение:
Проекцией вектора 
Обозначение:
Основные свойства проекций
- Проекция вектора АВ на какую-либо ось l равна произведению длины вектора на косинус угла между осью и этим вектором (рис. 25)
- Проекция суммы векторов на какую-либо ось l равна сумме проекций векторов на ту же ось.
Скалярное произведение векторов
Пусть имеем два вектора a и b.
Определение:
Скалярным произведением вектора а на вектор b называется число, обозначаемое символом (а, b) и определяемое равенством
(1)
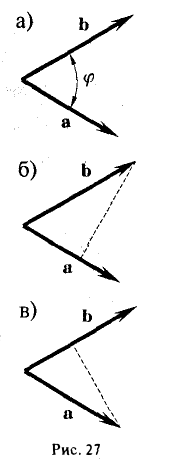
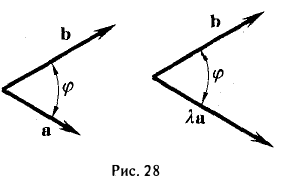
где φ, или в иной записи (
Заметив, что |b| cos φ есть проекция вектора b на направление вектора а, можем написать
(рис. 27 б) и, аналогично,’ (2)
(рис. 27 в), т.е. скалярное произведение двух векторов равно длине одного из них, помноженной на проекцию на него другого вектора. В случае, если один из векторов а или b — нулевой, будем считать, что
(a, b) = 0.
Свойства скалярного произведения
- Скалярное произведение обращается в нуль в том и только в том случае, когда по крайней мере один из перемножаемых векторов является нулевым или когда векторы а и b ортогональны, a ⊥ b.
Это следует из формулы (1), определяющей скалярное произведение.
Поскольку направление нулевого вектора не определено, мы можем его считать ортогональным любому вектору. Поэтому указанное свойство скалярного произведения можно сформулировать так:
2. Скалярное произведение коммутативно:
(а, b) = (b, а).
Справедливость утверждения вытекает из формулы (I), если учесть четность функции cos φ: cos(- φ) = cos φ.
3. Скалярное произведение обладает распределительным свойством относительно сложения:
(а + b, с) = (а, с) + (b, c).
4. Числовой множитель А можно выносить за знак скалярного произведения
(λа, b) = (а, λb) = λ (а, b).
- Действительно, пусть λ > 0. Тогда
поскольку при λ > 0 углы (

Аналогично рассматривается случай λ
Замечание:
В общeм случае (а, b)c ≠ a(b, c).
Скалярное произведение векторов, заданных координатами
Пусть векторы а и b заданы своими координатами в ортонормированном базисе i, j, k:
Рассмотрим скалярное произведение векторов а и b:
Пользуясь распределительным свойством скалярного произведения, находим
То есть, если векторы а и b заданы своими координатами в ортонормированном базисе, то их скалярное произведение равно сумме произведений одноименных координат.
Пример:
Найти скалярное произведение векторов n = 4i — 2j + k и b = 6i + 3j + 2k.
(a, b) = 4 • 6 + (-2) • 3 + 1 • 2 = 20.
Скалярное произведение вектора на себя называется скалярным квадратом:
(а, а) = а 2 .
Применяя формулу (4) при b = а, найдем (5)
С другой стороны,
так что из (5) следует, что (6)
— в ортонормированном базисе длина вектора равна квадратному корню из суммы квадратов его координат.
Косинус угла между векторами. Направляющие косинусы
Согласно определению
(а, b) = |а| • |b| • cos φ,
где φ — у гол между векторами а и b. Из этой формулы получаем
(7)
(предполагается, что векторы а и b — ненулевые).
Пример:
Найти угол между векторами a = и d = . Пользуясь формулой (8), находим
или, в координатной записи, (9)
где а есть угол, образованный вектором я с осью Ох. Аналогично получаем формулы
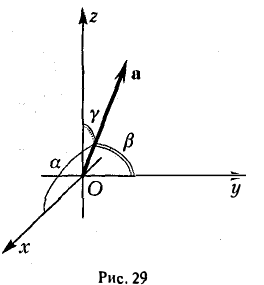
Формулы (9)-(11) определяют направляющие косинусы вектора а, т. е. косинусы углов, образуемых вектором n с осями координат (рис. 29).
Пример:
Найти координаты единичного вектора n°. По условию | n°| = 1. Пусть n° = zi+ yj+ zk. Тогда
Таким образом, координатами единичного вектора являются косинусы углов, образованных этим вектором с осями координат:
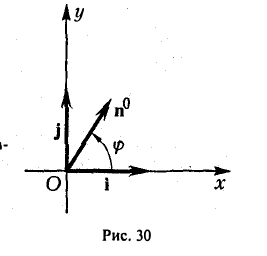
Пример:
Пусть единичный вектор n° ортогонален оси z:
(рис. 30). Тогда его координаты г и у соответственно равны
x=cos φ, y = sin φ.
Векторное произведение векторов
Определение:
Векторным произведением вектора а на вектор b называется вектор, обозначаемый символом [a, b] (или a х b), такой, что
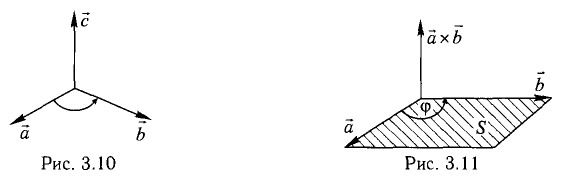
1) длина вектора [а, b] равна |а| • |Ь| • sin φ, где φ — угол между векторами а и b (рис.31);
2) вектор [а, b] перпендикулярен векторам а и b, т.е. перпендикулярен плоскости этих векторов;
3) вектор [а, Ь] направлен так, что из конца этого вектора кратчайший поворот от л к Ь виден происходящим против часовой стрелки (рис. 32).
Иными словами, векторы я, b и [a, b] образуют правую тройку векторов, т.е. расположены так, как большой, указательный и средний пальцы правой руки. В случае, если векторы a и b коллинеарны, будем считать, что [a, b] = 0.
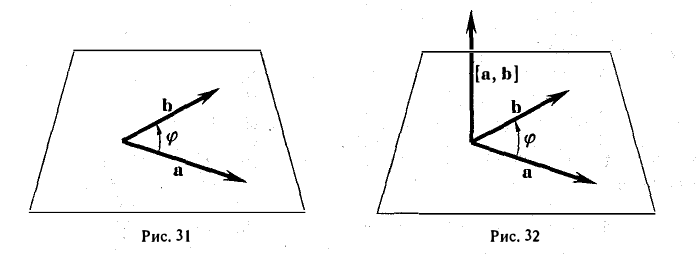
По определению длина векторного произведения (1)
численно равна площади 
|[a, b]| = 
Свойства векторного произведения
- Векторное произведение равно нулевому вектору тогда и только тогда, когда по крайней мере один из перемножаемых векторов является нулевым или когда эти векторы коллинеарны (если векторы я и b коллинеарны, то угол между ними равен либо 0, либо тг).
Это легко получить из того, что |[a, b]| = |a| • |b| • sin φ.
Если считать нулевой вектор коллинеарным любому вектору, то условие коллинеарности векторов a и b можно выразить так
2. Векторное произведение антикоммутативно, т. е. всегда (2)
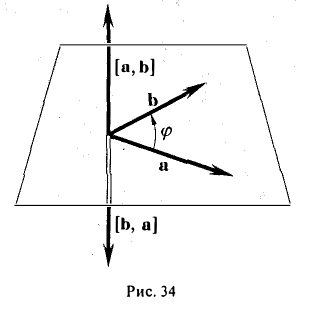
В самом деле, векторы [а, b] и [b, а] имеют одинаковую длину и коллинеарны. Направления же этих векторов противоположны, так как из конца вектора [a, b] кратчайший поворот от a к b будет виден происходящим против часовой стрелки, а из конца вектора [b, a] — почасовой стрелке (рис. 34).
3. Векторное произведение обладает распределительным свойством по отношению к сложению
4. Числовой множитель λ можно выносить за знак векторного произведения
Векторное произведение векторов, заданных координатами
Пусть векторы a и b заданы своими координатами в базисе i,j, k: а = < х1, у1, z1>, b = < х2, у2, z2 >. Пользуясь распределительным свойством векторного произведения, находим (3)
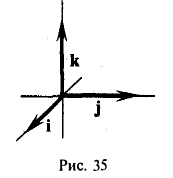
Выпишем векторные произведения координатных ортов (рис. 35):
Поэтому для векторного произведения векторов a и b получаем из формулы (3) следующее выражение (4)
Формулу (4) можно записать в символической, легко запоминающейся форме, если воспользоваться определителем 3-го порядка: (5)
Разлагая этот определитель по элементам 1-й строки, получим (4). Примеры:
- Найти площадь параллелограмма, построенного на векторах а = i + j- k, b = 2i + j- k.
Искомая площадь 
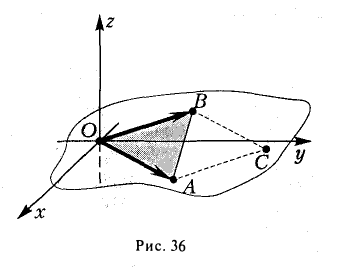
2. Найти площадь треугольника ОАВ (рис.36).
Ясно, что площадь S∆ треугольника ОАВ равна половине площади S параллелограмма О АС В. Вычисляя векторное произведение [a, b] векторов a= 

Замечание:
Векторное произведение не ассоциативно, т.е. равенство [[а, b], с] = [а, b,с]] в общем случае неверно. Например, при а = i, b = j. c= j имеем
Смешанное произведение векторов
Пусть имеем три вектора а, b и с. Перемножим векторы а и b векторно. В результате получим вектор [а, b). Умножим его скалярно на вектор с:
([a, b], с).
Число ([а, b], с) называется смешанным произведением векторов а, b, с и обозначается символом (а, b, с).
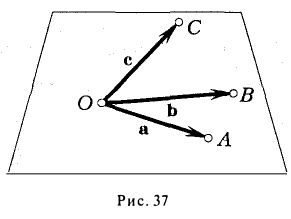
Геометрический смысл смешанного произведения
Отложим векторы а, b и с от общей точки О (рис. 37). Если все четыре точки О, А, В, С лежат в одной плоскости (векторы a, b и с называются в этом случае компланарными), то смешанное произведение ([а, b], с) = 0. Это следует из того, что вектор [а, b] перпендикулярен плоскости, в которой лежат векторы а и b, а значит, и вектору с.
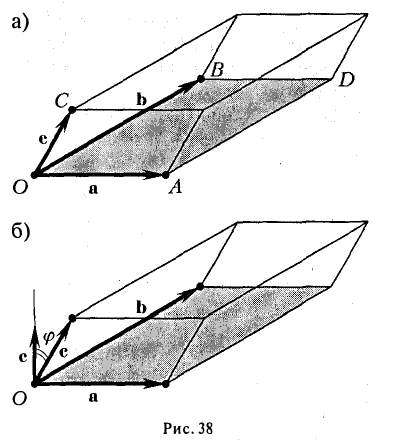
Если же точки О, А, В, С не лежат в одной плоскости (векторы a, b и с некомпланарны), построим на ребрах OA, OB и ОС параллелепипед (рис. 38 а). По определению векторного произведения имеем
где 
Умножая обе части последнего равенства справа скалярно на вектор с, получаем, что
Число ргe с равно высоте h построенного параллелепипеда, взятого со знаком « + », если угол ip между векторами с и с острый (тройка а, b, с — правая), и со знаком «-», если угол — тупой (тройка а, b, с — левая), так что
Тем самым, смешанное произведение векторов a, b и с равно объему V параллелепипеда, построенного на этих векторах как на ребрах, если тройка а, b, с — правая, и -V, если тройка а, b, с — левая.
Исходя из геометрического смысла смешанного произведения, можно заключить, что, перемножая те же векторы a, b и с в любом другом порядке, мы всегда будем О получать либо +V, либо -V. Знак произведения будет зависеть лишь от того, какую тройку образуют перемножаемые векторы — правую или левую. Если векторы а, b, с образуют правую тройку, то правыми будут также тройки b, с, а и с, а, b. В то же время все три тройки b, а, с; а, с, b и с, b, а — левые. Тем самым,
(а, b, с) = (b, с, а) = (с, a,b) = -(b, а, с) = -(а, с, b) = -(с, b, а).
Еще раз подчеркнем, что смешанное произведение векторов равно нулю тогда и только тогда, когда перемножаемые векторы а, b, с компланарны:
Смешанное произведение в координатах
Пусть векторы а, b, с заданы своими координатами в базисе i, j, k:
Найдем выражение для их смешанного произведения (а, b, с). Имеем
— смешанное произведение векторов, заданных своими координатами в базисе i, j, k, равно определителю третьего порядка, строки которого составлены соответственно из координат первого, второго и третьего из перемножаемых векторов.
Пример:
Проверить, компланарны ли векторы
Рассматриваемые векторы будут компланарны или некомпланарны в зависимости от того, будет равен нулю или нет определитель
Разлагая его по элементам первой строки, получим
Двойное векторное произведение
Двойное векторное произведение [а, [b, с]] представляет собой вектор, перпендикулярный к векторам а и [b, с]. Поэтому он лежит в плоскости векторов b и с и может быть разложен по этим векторам. Можно показать, что справедлива формула
[а, [b, с]] = b(а, с) — с(а, b).
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
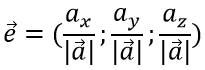
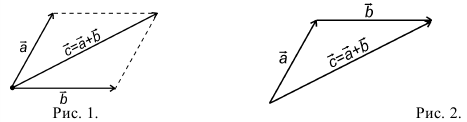
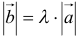 ;
;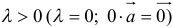 .
.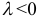 .
.