1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;
2) система линейных неравенств, определяющих треугольник;
2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;
3) внутренние углы по теореме косинусов;
4) площадь треугольника;
5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;
10) параметры вписанной и описанной окружностей и их уравнения.
Внимание! Этот сервис не работает в браузере IE (Internet Explorer).
Запишите координаты вершин треугольника и нажмите кнопку.
| A ( ; ), B ( ; ), C ( ; ) | Примечание: дробные числа записывайте Округлять до -го знака после запятой. Содержание Видео:Уравнения стороны треугольника и медианыСкачать  Расчет треугольника по координатам вершинЭтот онлайн калькулятор по введенным координатам вершин вычисляет параметры треугольника: длины сторон, углы, периметр и площадь. Этот онлайн калькулятор предназначен для быстрого вычисления ряда характеристик треугольника по координатам его вершин. Вы вводите координаты вершин A, B и C. Калькулятор рассчитывает по координатам следующие величины:
Если нужно что-то еще, пишите в комментариях, добавим. Формулы расчета значений треугольника описаны под калькулятором. Видео:Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать  Уравнение длины сторон треугольника – по координатам и сторонамУравнение длин сторон треугольника – это первые вкрапления высшей математики в математику школьного курса. Понимание данной тематики приближает ученика к университетскому уровню, вместе с тем делая более понятной тему функции. Видео:Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать  ФункцияЧто такое функция? Это зависимость одной величины от другой. В математической функции чаще всего две неизвестных: независимая и зависимая или х и у соответственно. Что это значит? Это значит, что х может принимать абсолютно любое значение, а у будет под него подстраиваться, меняясь в соответствии с коэффициентами функции. Существуют ситуации, когда функция имеет несколько переменных. Зависимая у всегда 1, но факторов, которые влияют на неё может быть несколько. Не всегда такую функцию получается отразить на графике. В лучшем случае графически можно отобразить зависимость у от 2 переменных. Как проще всего представить зависимость у(х)? Да очень просто. Представьте себе избалованного ребенка и богатую любящую мать. Они вместе приходят в магазин и начинают клянчить конфеты. Кто знает, сколько конфет мальчик потребует сегодня? Никто, но в зависимости от количества конфет увеличится сумма, которую мама оплатит на кассе. В этом случае, зависимой величиной является сумма в чеке, а независимой – количество конфет, которое захочет мальчик сегодня. Очень важно понимать, что одному значению функции у, всегда соответствует 1 значение аргумента х. Но, как и с корнями квадратного уравнения, эти значения могут совпадать. Видео:№942. Найдите медиану AM треугольника ABC, вершины которого имеют координаты: А(0; 1), В(1; -4)Скачать  Уравнение прямой линииЗачем нам нужно уравнение прямой, если мы говорим об уравнении длин сторон треугольника? Да затем, что каждая из сторон треугольника это отрезок. А отрезок это ограниченная часть прямой. То есть мы можем задать уравнения прямых. А в точках их пересечения ограничить линии, тем самым обрезав прямые и превратив их в отрезки. Уравнение прямой выглядит следующим образом: Видео:Математика без Ху!ни. Смешанное произведение векторовСкачать  Уравнение сторон треугольникаНеобходимо найти уравнение длин сторон треугольника с вершинами в точках А(3,7) ; В(5,3); С(12;9)
Поочередно составим уравнения каждой из линий треугольника.
Из первого уравнения выразим b и подставим во второе. 🌟 ВидеоКоординаты вектора. 9 класс.Скачать  Вычисляем высоту через координаты вершин 1Скачать  Метод координат. Как найти медиану треугольника, если известны координаты его вершин?Скачать  №1049. Найдите углы треугольника с вершинами А (-1; √3), В(1;-√3 )Скачать  Нахождение длины отрезка по координатамСкачать  Вычисляем угол через координаты вершинСкачать  Вычисление медианы, высоты и угла по координатам вершинСкачать  Длина вектора через координаты. 9 класс.Скачать  Нахождение координат вектора. Практическая часть. 9 класс.Скачать  Координаты середины отрезкаСкачать  Даны вершины пирамиды A, B, C, D. Найдите объём пирамиды и высоту, опущенную на грань ACDСкачать  Угол между векторами | МатематикаСкачать  Координаты точки и координаты вектора 1.Скачать  Площадь треугольника, построенного на векторахСкачать  Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать  | ||
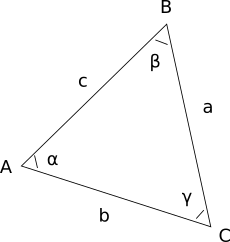 Обозначения треугольника
Обозначения треугольника