Как найти длины диагоналей параллелограмма построенного по векторам

Математика | 10 — 11 классы

Вычислите длины диагоналей параллелограмма, построенного на векторах a = 2m + n и b = m — 2n , где m и n ― единичные векторы, угол между которыми o 60 .

d1 = 2m + n + m — 2n = 3m — n

|d1|² = (3m — n)(3m — n) = 9m² — 6mn + n² = 9|m|² — 6|m||n|cosa + |n|² = 9 * 1 — 6 * 1 * 1 * 1 / 2 + 1 = 9 — 3 + 1 = 7

d2 = 2m + n — m + 2n = m + 3n

|d2|² = (m + 3n(m + 3n) = m² + 6mn + 9n² = |m|² + 6|m||n|cosa + 9|n|² = 1 + 6 * 1 * 1 * 1 / 2 + 9 * 1 = 1 + 3 + 9 = 13.

Видео:Найти угол между векторами и площадь параллелограмма, построенного на этих векторахСкачать

Вычислить длины диагоналей и площадь параллелограмма, построенного на векторах : Полное решение?

Вычислить длины диагоналей и площадь параллелограмма, построенного на векторах : Полное решение.

Видео:Площадь параллелограмма, построенного на данных векторахСкачать

Параллелограмм построен на векторах а = (1 ; 2 ; — 3) b = (2 ; — 1 ; — 1), нужно определить косинус угла между диагоналями и найти длину высоты, опущенной на вектор а?

Параллелограмм построен на векторах а = (1 ; 2 ; — 3) b = (2 ; — 1 ; — 1), нужно определить косинус угла между диагоналями и найти длину высоты, опущенной на вектор а.

Видео:Найдите длины диагоналей параллелограмма, построенного на векторах a=(1;-1;-4) и b=(-5;3;8)Скачать

Найдите координаты вектора единичной длины, коллинеарного прямой 3x — 2y + 1 = 0?

Найдите координаты вектора единичной длины, коллинеарного прямой 3x — 2y + 1 = 0.

Видео:Площадь параллелограмма по векторамСкачать

Дан параллелограмм ABCD?

Дан параллелограмм ABCD.

Найдите сумму векторов вектор АВи АD.

Видео:Сумма квадратов диагоналей параллелограммаСкачать

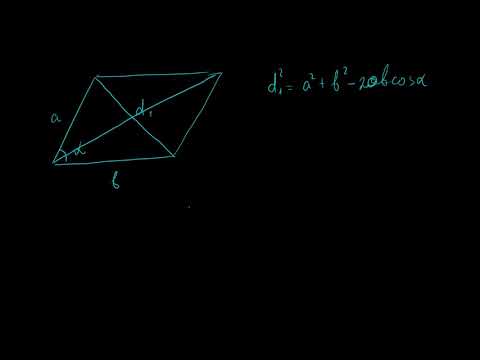
Вычислить длину вектора а?

Вычислить длину вектора а.

Видео:Найдите площадь параллелограмма, построенного на векторахСкачать

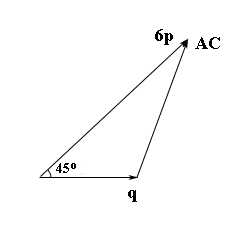
Найдите а вектор * в вектор если угол между векторами равен 45° ?

Найдите а вектор * в вектор если угол между векторами равен 45° .

Вектор а = √2, вектор в = 6.

Видео:1. Векторы и параллелограмм задачи №1Скачать

Четырехугольник АВСD — параллелограмм , О — точка пересечения его диагоналей?

Четырехугольник АВСD — параллелограмм , О — точка пересечения его диагоналей.

Назовите вектор с началом О , равный вектору — OD.

Видео:Задача 4. Вычислить площадь параллелограмма, построенного на векторах.Скачать

Дана система координат Oe1e2 , причем |e1| = 2, |e2| = корень из 3 , угол между ними равен 5pi / 6 ?

Дана система координат Oe1e2 , причем |e1| = 2, |e2| = корень из 3 , угол между ними равен 5pi / 6 .

Найти угол между векторами a(1 ; 2) и b(2 ; 2) и площадь параллелограмма, построенного на векторах a и b.

Видео:2. Векторы в параллелограмме Решение задач №2Скачать

Найдите угол между диагоналями параллелограмма построенного на векторах p = 2a — b b q = a + b как на сторонах если a и b единичные векторы и угол между векторами a и b = 60°?

Найдите угол между диагоналями параллелограмма построенного на векторах p = 2a — b b q = a + b как на сторонах если a и b единичные векторы и угол между векторами a и b = 60°.

Видео:§20 Нахождение объёма параллелипипедаСкачать

Дан параллелограмм ABCD?

Дан параллелограмм ABCD.

Выразите вектор ba через векторы bc и ac.

На этой странице сайта размещен вопрос Вычислите длины диагоналей параллелограмма, построенного на векторах a = 2m + n и b = m — 2n , где m и n ― единичные векторы, угол между которыми o 60 ? из категории Математика с правильным ответом на него. Уровень сложности вопроса соответствует знаниям учеников 10 — 11 классов. Здесь же находятся ответы по заданному поиску, которые вы найдете с помощью автоматической системы. Одновременно с ответом на ваш вопрос показаны другие, похожие варианты по заданной теме. На этой странице можно обсудить все варианты ответов с другими пользователями сайта и получить от них наиболее полную подсказку.

Решение на фото. Сначала посчитана разность в скобках, а потом все остальное.

Видео:Математика без Ху!ни. Смешанное произведение векторовСкачать

Математический портал

Видео:как найти площадь параллелограмма построенного на векторахСкачать

Nav view search

Navigation

Search

• Вы здесь:
• Home
• Векторная алгебра.
• Высшая математика.
• Векторная алгебра.
• Скалярное произведение векторов, свойства. Длина вектора. Угол между векторами.

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Скалярное произведение векторов, свойства. Длина векторов. Угол между векторами.

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

Видео:Угол между векторами | МатематикаСкачать

Длина вектора.

Пусть вектор $overline a=(x, y, z)$ представлен своими координатами в прямоугольном базисе. Тогда его длину можно вычислить по формуле $$|overline a|=sqrt.$$

Видео:Свойства диагоналей параллелограмма | Геометрия 8-9 классыСкачать

Скалярное произведение векторов.

Если заданы координаты точек $A(x_1, y_1, z_1) $ и $B(x_2, y_2, z_2),$ то координаты вектора $overline$ можно найти по формулам $$overline=(x_2-x_1, y_2-y_1, z_2-z_1).$$ Скалярным произведением ненулевых векторов $a_1$ и $a_2$ называется число $$(a_1, a_2)=|a_1||a_2|cos(widehat).$$

Для скалярного произведения наряду с обозначением $(a_1,a_2)$ используется также обозначение $a_1a_2.$

Видео:Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Геометрические свойства скалярного произведения:

1) $a_1perp a_2Leftrightarrow a_1a_2=0$ (условие перпендикулярности векторов).

2) Если $varphi=(widehat),$ то $$0leqvarphi 0; qquadqquad frac

Видео:Площадь треугольника, построенного на векторахСкачать

Алгебраические свойства скалярного произведения:

2) $(lambda a_1)a_2=lambda (a_1 a_2);$

Если векторы $a_1(X_1, Y_1, Z_1)$ и $a_2(X_2, Y_2, Z_2)$ представлены своими координатами в прямоугольном базисе, то скалярное произведение равно $$a_1a_2=X_1X_2+Y_1Y_2+Z_1Z_2. $$

Видео:6 способов построения параллелограмма.Скачать

Из этой формулы, в частности, следует формула для определения косинуса угла между векторами:

Решение.

а) $$a_1^2=(a_1, a_1)=|a_1||a_1|cos(widehat)=|a_1|^2=3^2=9.$$

б) $(3a_1-2a_2)(a_1+2a_2);$

Поскольку скалярное произведение зависит от длин векторов и угла между ними, то заданные векторы можно выбрать произвольно учитывая эти характеристики. Пусть $a_1=(3; 0). $ Тогда вектор $a_2,$ имея длину $|a_2|=4,$ и, образуя угол $frac$ с положительной полуосью оси $OX,$ имеет координаты $x=|a_2|cosfrac=-frac=-2; $

$3a_1-2a_2=3(3;0)-2(-2;2sqrt 3)=(9;0)-(-4; 4sqrt 3)=(13;-4sqrt 3);$

$a_1+2a_2=(3; 0)+2(-2;2sqrt 3) = (3; 0)+ (-4; 4sqrt 3)= (-1; 4sqrt 3).$

$(3a_1-2a_2)(a_1+2a_2)=(13; -4sqrt 3)(-1; 4sqrt 3) =-13-48=-61.$

в) $(a_1+a_2)^2.$

$a_1+a_2$=$(3; 0)+(-2; 2sqrt 3)=(1; 2sqrt 3).$

$(a_1+a_2)^2=(1; 2sqrt3) (1; 2sqrt 3)=1+12=13.$

Ответ: a) 9; б) -61; в) 13.

2.67. Вычислить длину диагоналей параллелограмма, построенного на векторах $a=p-3q, $ $b=5p+2q,$ если известно, что $|p|=2sqrt, |q|=3, (widehat

)=frac.$

Решение.

Способ 1.

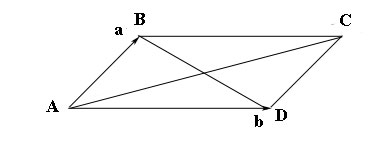
Из треугольника $ABC$ имеем $AC=AB+BC=a+b=p-3q+5p+2q=6p-q.$

Зная длину векторов $p$ b $q$ и угол между этими векторами, можно найти длину вектора $AC$ по теореме косинусов:

Из треугольника $ABD$ имеем: $BD=AD-AB=b-a=5p+2q-p+3q=4p+5q.$

По теореме косинусов находим длину вектора $BD:$

$|BD|^2=|4p|^2+|5q|^2-8p5qcos widehat=$ $128+225+240=593.$

Пусть $q=(3; 0). $ Тогда вектор $p,$ имея длину $|p|=2sqrt 2,$ и образуя угол $frac$ с положительной полуосью оси $OX$ имеет координаты

Из треугольника $ABC$ имеем

Из треугольника $ABD$ имеем

$BD=AD-AB=b-a=5p+2q-p+3q=4p+5q=$ $=4(2; 2)+5(3;0)=(8; 8)+(15; 0)=(23; 8).$

Ответ: $15, sqrt .$

2.68. Определить угол между векторами $a$ и $b$ если известно, что $(a-b)^2+(a+2b)^2=20$ и $|a|=1, |b|=2.$

Ответ: $2pi/3$

$|a_1|=3; |a_2|=5. $ Определить, при каком значении $alpha$ векторы $a_1+alpha a_2$ и $a_1-alpha a_2$ будут перпендикулярны.

Ответ: $alpha=pmfrac$

В треугольнике $ABC$ $overline=3e_1-4e_2;$ $overline=e_1+5e_2.$ Вычислить длину его высоты $overline,$ если известно, что $e_1$ и $e_2$ взаимно перпендикулярные орты.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Задача 32233 Определить длины диагоналей.

Условие

Определить длины диагоналей параллелограмма, построенного на векторах [b]a=2m+n[/b] и [b]b=m-2n[/b], где [b]m[/b] и [b]n[/b]-единичные векторы, угол между которыми 60 градусов.

Все решения

=(3vector-vector)^2=9vector*vector-6vectorvector+
vector*vector=9*1*1cos0^(o)-6*1*1*cos60^(o)+1*1*cos0^(o)=
=9-3+1=7
|vector|=sqrt(7)

=(vector+3vector)^2=vector*vector+6vectorvector+
9vector*vector=*1*1cos0^(o)+6*1*1*cos60^(o)+9*1*1*cos0^(o)=
=1+3+9=13
|vector|=sqrt(13)

🔥 Видео

№497. Одна из диагоналей параллелограмма является его высотой. Найдите эту диагональ, если периметрСкачать