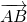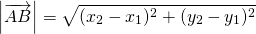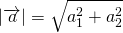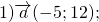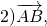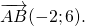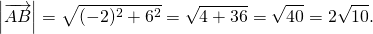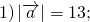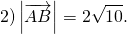Как найти абсолютную величину вектора по его координатам (6 видео)

Планиметрия. Страница 8

1 2 3 4 5 6 7 8 9 10 11 12

Как найти абсолютную величину вектора по его координатам

Содержание

1.Вектор и его абсолютная величина
Координаты вектора
2.Сложение векторов
3.Умножение вектора на число
6.Пример 1
Пример 2
Пример 3
Пример 4
Пример 5
Вектор. Модуль вектора. Длина вектора.
Длина вектора
🔍 Видео

Видео:Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать

1.Вектор и его абсолютная величина

Вектором называется направленный отрезок определенной длины. Любой вектор имеет начальную и конечную точки. Начало и конец вектора обозначаются заглавными буквами, например вектор

. Сам вектор обозначается прописной буквой, например:

. Каждый вектор имеет определенную длину и направление. Например, вектора

имеют одинаковое направление. А вектора

Абсолютной величиной вектора или модулем вектора называется длина отрезка, представляющего собой вектор.

Если начало вектора совпадает с его концом, то такой вектор называется нулевым.

Если два вектора имеют одинаковое направление и равные абсолютные величины, то такие векторы называются равными.

Рис.1 Обозначение векторов.

Видео:Тема 7.2. Координаты вектора. Абсолютная величина.Скачать

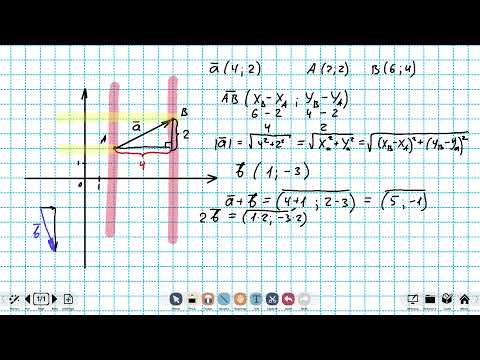
Координаты вектора

Любой вектор имеет свои координаты. Координатами вектора называются числа x₂-x₁ и y₂-y₁. Например, координаты вектора

с начальной точкой А (1;1) и конечной точкой В (4;3) будут:

Координаты нулевого вектора равны нулю.

Абсолютная величина вектора — это его длина. А следовательно, ее можно определить как расстояние между двумя точками, начальной и конечной. Т.е.

Два вектора называются равными, если у них соответствующие координаты равны.

Рис.2 Координаты вектора.

Видео:Абсолютная величина вектора. Равенство векторов.Скачать

2.Сложение векторов

Пусть заданы два вектора со своими координатами

(b₁;b₂). Тогда суммой двух векторов будет вектор с координатами

В векторной форме можно записать так:

Для сложения векторов используются два метода: метод треугольника и метод параллелограмма.

Для сложения векторов методом треугольника необходимо перенести вектор

параллельным переносом так, чтобы конец вектора

совпадал с началом вектора

. Тогда начало вектора

и конец вектора

и будет сумма векторов

По методу параллелограмма, если два вектора

имеют общее начало, то суммой двух векторов будет диагональ параллелограмма, построенного на этих векторах, т.е. вектор

Разностью двух векторов

называется такой вектор

, который нужно прибавить к вектору

, чтобы получить вектор

Рис.3 Сложение векторов.

Видео:Абсолютная величина вектораСкачать

3.Умножение вектора на число

Любой вектор с координатами (x;y) можно умножить на простое число, например λ. (Рис.3) Тогда произведением вектора на число λ будет называться вектор с координатами (λx;λy). Абсолютная величина вектора будет равна:

Для любых двух векторов

число λ можно вынести за скобку λ (

Если λ > 0, то направление вектора не изменяется, а если λ 2 и называется скалярным квадратом. Отсюда следует, что

Теорема. Скалярное произведение двух векторов равно произведению их абсолютных величин на косинус угла между ними.

Доказательство. Пусть даны два вектора а и b и угол между ними α. Тогда квадрат суммы двух векторов равен:

Следовательно, скалярное произведение двух векторов не зависит от выбора системы координат, а зависит только от их абсолютных величин. (Рис.5)

Так как координаты вектора

(b cos α; b sin α), то скалярное произведение двух векторов

Рис.5 Скалярное произведение векторов.

Отсюда вытекает следующий вывод:

если два вектора перпендикулярны, то их скалярное произведение равно нулю.

если скалярное произведение двух ненулевых векторов равно нулю, то векторы перпендикулярны.

6.Пример 1

Четырехугольник ABCD — параллелограмм. Докажите равенство векторов

Доказательство:

Пусть ABCD данный параллелограмм (Рис.6). Необходимо доказать, что вектора

параллельному переносу таким образом, чтобы точка А совпала с точкой D. При таком перемещении точка А смещается по прямой AD и переходит в точку D. Это значит, что точка В переместится по параллельной прямой ВС в точку С.

Таким образом, при параллельном переносе прямая АВ переходит в параллельную прямую DC, а вектор

переходит в вектор

. А это значит, что эти вектора равны.

Действительно, так как при перемещении прямая АВ переходит в параллельную прямую DC, а точка А переходит в точку D, то на луче DC можно отложить только один вектор, равный вектору

Рис.6 Задача. Четырехугольник ABCD — параллелограмм.

Пример 2

Даны точки А(1;1), B(3;1), C(2;-2), D(4;-2). Докажите равенство векторов

Доказательство:

Найдем координаты векторов

Таким образом, координаты векторов следующие:

А так как равные вектора имеют равные соответствующие координаты и x_AB = x_CD, y_AB = y_CD, то вектора

Рис.7 Задача. Даны точки А(1;1), B(3;1), C(2;-2), D(4;-2).

Пример 3

В треугольнике АВС проведена медиана AM. Докажите, что

Доказательство:

, равный и параллельный вектору

от точки С. И отложим вектор

, равный и параллельный вектору

от точки В (Рис.8).

Тодга получим параллелограмм, в котором вектор

, так же как вектор

. А так как диагонали параллелограмма пересекаются в точке М и делятся этой точкой пополам, то

Отсюда можно сделать вывод: так как

Рис.8 Задача. В треугольнике АВС проведена медиана AM.

Пример 4

(-3;-2). Найдите вектор

и его абсолютную величину.

Решение:

, то найдем его координаты:

Теперь найдем его абсолютную величину:

| 2 = (-1) 2 + (-4) 2 = 17

| =

(-3;-2). » alt=»Задача. Даны векторы

Рис.9 Задача. Даны векторы

Пример 5

Найдите угол между векторами

Решение:

По определению, скалярное произведение двух векторов равно произведению их абсолютных величин на косинус угла между ними. Отсюда можно найти косинус угла между ними по формуле:

Следовательно, cos α = 2 / 2 = 1 /

Таким образом, угол между векторами

(1;-1) и b (2;0).» alt=»Задача. Найдите угол между векторами

(1;-1) и b (2;0).» src=»http://www.mathtask.ru/page-0056/pl21.png»/>

Рис.10 Задача. Найдите угол между векторами

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Вектор. Модуль вектора. Длина вектора.

Длина вектора и модуль вектора это тождественные понятия выражающее числовое значение длины направленного отрезка.

Квадрат длины любого вектора равен сумме квадратов его координат.

Для доказательства этой теоремы возьмем произвольный вектор . Затем опустим перпендикуляр на ось абсцисс и ось ординат. Получим проекции выбранного вектора на координатной оси и прямоугольный треугольник в котором гипотенуза заданный нами вектор. Далее применим теорему Пифагора, согласно которой квадрат гипотенузы равен сумме квадратов катетов.