Как находить векторы в параллелограмме

Видео:Сложение векторов. Правило параллелограмма. 9 класс.Скачать

Правило параллелограмма — что это такое

Чтобы сложить два вектора можно воспользоваться правилом параллелограмма.

Правило параллелограмма: если два неколлинеарных вектора a и b привести к общему началу, то вектор c=a+b совпадает с диагональю параллелограмма, построенного на векторах a и b. Начало вектора c совпадает с началом этих векторов.

Кроме того, по правилу параллелограмма можно осуществлять вычитание.

Видео:1. Векторы и параллелограмм задачи №1Скачать

Сложение векторов по правилу параллелограмма

Для того чтобы сложить два вектора по правилу параллелограмма, необходимо:

1. Взять произвольную точку А.
2. Отложить от точки векторы a и b.
3. Построить на векторах a и b параллелограмм.
4. Диагональ параллелограмма и будет суммой векторов a+b

Также существуют еще два правила нахождения векторной суммы:

1. Правило треугольника.

Чтобы сложить два вектора, нужно из произвольной точки отложить первый вектор, из его конца отложить второй вектор и построить вектор, который соединит начало первого с концом второго. Полученный вектор — искомая сумма.

2. Правило многоугольника.

Чтобы сложить несколько векторов, нужно от произвольной точки отложить первый вектор, из его конца — второй вектор, из конца второго — третий, и так далее. Затем соединить начальную точку с концом последнего вектора, полученный вектор — искомая сумма.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Переместительный и сочетательный законы, доказательство

Для более ясного понимания правила параллелограмма, важно знать законы сложения векторов.

Переместительный закон: от перемены мест слагаемых сумма не меняется a+b=b+a.

От произвольной точки A отложим векторы AB=a и AD=b.

Построим параллелограмм ABCD.

По правилу треугольника заметим: AC=AB+BC, то есть равен сумме векторов a+b.

AC=AB+BC, AC=a+b⇒ a+b=b+a.

С другой стороны, AC=AD+DC, AC=b+a.

Что и требовалось доказать.

Именно переместительный закон применяется в правиле параллелограмма.

Сочетательный закон: (a+b)+c=a+(b+c).

От произвольной точки A отложим вектор AB=a, от точки B вектор BC=b, от точки C вектор CD=c.

Запишем сумму (a+b)+c через векторы:

Сумма AB+BC=AC (по правилу треугольника).

Запишем сумму a+(b+c) через векторы:

Что и требовалось доказать.

Видео:8 класс, 44 урок, Законы сложения векторов. Правило параллелограммаСкачать

Примеры решения задач

Дан параллелограмм, построенный на векторах AB=6 см, BC=8 см. ∠B=90º. Найти сумму векторов AB+BC.

По правилу параллелограмма сумма векторов AB+BC=BD.

BD-диагональ параллелограмма. Диагональ можно найти по формуле:

B D = √ ( A B ² + B C ² — 2 * A B * B C * cos B ) .

ABCD — прямоугольник, так как ∠B=90º ⇒cosB=0.

Видео:№770. Дан параллелограмм ABCD. Выразите вектор АС через векторы а и b , если:Скачать

Векторы на ЕГЭ по математике. Действия над векторами

Стандартное определение: «Вектор — это направленный отрезок». Обычно этим и ограничиваются знания выпускника о векторах. Кому нужны какие-то «направленные отрезки»?

А в самом деле, что такое векторы и зачем они?
Прогноз погоды. «Ветер северо-западный, скорость 18 метров в секунду». Согласитесь, имеет значение и направление ветра (откуда он дует), и модуль (то есть абсолютная величина) его скорости.

Величины, не имеющие направления, называются скалярными. Масса, работа, электрический заряд никуда не направлены. Они характеризуются лишь числовым значением — «сколько килограмм» или «сколько джоулей».

Физические величины, имеющие не только абсолютное значение, но и направление, называются векторными.

Скорость, сила, ускорение — векторы. Для них важно «сколько» и важно «куда». Например, ускорение свободного падения направлено к поверхности Земли, а величина его равна 9,8 м/с 2 . Импульс, напряженность электрического поля, индукция магнитного поля — тоже векторные величины.

Вы помните, что физические величины обозначают буквами, латинскими или греческими. Стрелочка над буквой показывает, что величина является векторной:

Вот другой пример.
Автомобиль движется из A в B . Конечный результат — его перемещение из точки A в точку B , то есть перемещение на вектор .

Теперь понятно, почему вектор — это направленный отрезок. Обратите внимание, конец вектора — там, где стрелочка. Длиной вектора называется длина этого отрезка. Обозначается: или

До сих пор мы работали со скалярными величинами, по правилам арифметики и элементарной алгебры. Векторы — новое понятие. Это другой класс математических объектов. Для них свои правила.

Когда-то мы и о числах ничего не знали. Знакомство с ними началось в младших классах. Оказалось, что числа можно сравнивать друг с другом, складывать, вычитать, умножать и делить. Мы узнали, что есть число единица и число ноль.
Теперь мы знакомимся с векторами.

Понятия «больше» и «меньше» для векторов не существует — ведь направления их могут быть разными. Сравнивать можно только длины векторов.

А вот понятие равенства для векторов есть.
Равными называются векторы, имеющие одинаковые длины и одинаковое направление. Это значит, что вектор можно перенести параллельно себе в любую точку плоскости.
Единичным называется вектор, длина которого равна 1 . Нулевым — вектор, длина которого равна нулю, то есть его начало совпадает с концом.

Удобнее всего работать с векторами в прямоугольной системе координат — той самой, в которой рисуем графики функций. Каждой точке в системе координат соответствуют два числа — ее координаты по x и y , абсцисса и ордината.
Вектор также задается двумя координатами:

Здесь в скобках записаны координаты вектора — по x и по y .
Находятся они просто: координата конца вектора минус координата его начала.

Если координаты вектора заданы, его длина находится по формуле

Видео:Выразить векторы. Разложить векторы. Задачи по рисункам. ГеометрияСкачать

Сложение векторов

Для сложения векторов есть два способа.

1 . Правило параллелограмма. Чтобы сложить векторы и , помещаем начала обоих в одну точку. Достраиваем до параллелограмма и из той же точки проводим диагональ параллелограмма. Это и будет сумма векторов и .

Помните басню про лебедя, рака и щуку? Они очень старались, но так и не сдвинули воз с места. Ведь векторная сумма сил, приложенных ими к возу, была равна нулю.

2 . Второй способ сложения векторов — правило треугольника. Возьмем те же векторы и . К концу первого вектора пристроим начало второго. Теперь соединим начало первого и конец второго. Это и есть сумма векторов и .

По тому же правилу можно сложить и несколько векторов. Пристраиваем их один за другим, а затем соединяем начало первого с концом последнего.

Представьте, что вы идете из пункта А в пункт В , из В в С , из С в D , затем в Е и в F . Конечный результат этих действий — перемещение из А в F .

При сложении векторов и получаем:

Видео:Площадь параллелограмма, построенного на данных векторахСкачать

Вычитание векторов

Вектор направлен противоположно вектору . Длины векторов и равны.

Теперь понятно, что такое вычитание векторов. Разность векторов и — это сумма вектора и вектора .

Видео:2. Векторы в параллелограмме Решение задач №2Скачать

Умножение вектора на число

При умножении вектора на число k получается вектор, длина которого в k раз отличается от длины . Он сонаправлен с вектором , если k больше нуля, и направлен противоположно , если k меньше нуля.

Видео:Вычитание векторов. 9 класс.Скачать

Скалярное произведение векторов

Векторы можно умножать не только на числа, но и друг на друга.

Скалярным произведением векторов называется произведение длин векторов на косинус угла между ними.

Обратите внимание — перемножили два вектора, а получился скаляр, то есть число. Например, в физике механическая работа равна скалярному произведению двух векторов — силы и перемещения:

Если векторы перпендикулярны, их скалярное произведение равно нулю.
А вот так скалярное произведение выражается через координаты векторов и :

Из формулы для скалярного произведения можно найти угол между векторами:

Эта формула особенно удобна в стереометрии. Например, в задаче 14 Профильного ЕГЭ по математике нужно найти угол между скрещивающимися прямыми или между прямой и плоскостью. Часто векторным методом задача 14 решается в несколько раз быстрее, чем классическим.

В школьной программе по математике изучают только скалярное произведение векторов.
Оказывается, кроме скалярного, есть еще и векторное произведение, когда в результате умножения двух векторов получается вектор. Кто сдает ЕГЭ по физике, знает, что такое сила Лоренца и сила Ампера. В формулы для нахождения этих сил входят именно векторные произведения.

Векторы — полезнейший математический инструмент. В этом вы убедитесь на первом курсе.

Онлайн-курс «Математика 10+11 100 баллов»

— Теория: учебник Анны Малковой + 70 ч. видеоразборов.
— 144 ч. мастер-классов: 8 онлайн мастер-классов с Анной Малковой в месяц.
— Тренажер для отработки задач ЕГЭ (800+ задач): автоматическая + ручная проверки.
— Связь с Анной Малковой (чаты и почта).
— 9 репетиционных ЕГЭ: ежемесячно.
— Контроль: страница личных достижений учащегося, отчеты родителям.
— Личный кабинет.

Видео:ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать

Сложение и вычитание векторов

Теорема 1 От любой точки ( K ) можно отложить вектор единственный ( overrightarrow ) .

Существование: Имеем два следующих случая:

Здесь получаем, что искомый нами вектор совпадает с вектором ( overrightarrow ) .

Из данного выше построения сразу же будет следовать единственность данного вектора.

Видео:Найдите площадь параллелограмма, построенного на векторахСкачать

Сумма векторов. Сложение векторов. Правило треугольника

Сложение векторов выполняется по правилу треугольника или по правилу параллелограмма.

Суммой нескольких векторов ( vec ) , ( vec ) , ( vec,;ldots ) называется вектор ( vec ) , получающийся в результате последовательного сложения данных векторов.

Такая операция выполняется по правилу многоугольника.

Сумма векторов в координатах
При сложении двух векторов соответствующие координаты складываются.
( vec + vec = left( <+ , + , + > right) )

Отметим несколько свойств сложения двух векторов:

Для произвольного вектора ( overrightarrow ) выполняется равенство

Для произвольных точек ( A, B и C ) справедливо следующее равенство

Замечание Таким способом также можно строить сумму любого числа векторов. Тогда оно будет носить название правила многоугольника.

Видео:№933. Найдите координаты вершины D параллелограмма ABCD, если А (0; 0), B (5; 0), С (12; -3.).Скачать

Разность векторов. Вычитание векторов

Разность двух одинаковых векторов равна нулевому вектору :
( vec — vec = vec )

Длина нулевого вектора равна нулю:
( left| vec right| = 0 )

Разность векторов в координатах
При вычитании двух векторов соответствующие координаты также вычитаются.
( vec — vec = left( <- , — , — > right) )

Видео:Площадь параллелограмма по векторамСкачать

Умножение вектора на число

Пусть нам дан вектор ( overrightarrow ) и действительное число ( k ) .

Определение Произведением вектора ( overrightarrow ) на действительное число ( k ) называется вектор ( overrightarrow ) удовлетворяющий следующим условиям:

Длина вектора ( overrightarrow ) равна ( left|overrightarrowright|=left|kright||overrightarrow| ) ;

Векторы ( overrightarrow ) и ( overrightarrow ) сонаправлены, при ( kge 0 ) и противоположно направлены, если ( kle 0 )

Обозначение: ( overrightarrow=koverrightarrow ) .

🔍 Видео

как найти площадь параллелограмма построенного на векторахСкачать

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

№748. Диагонали параллелограмма ABCD пересекаются в точке O. Равны ли векторы?Скачать

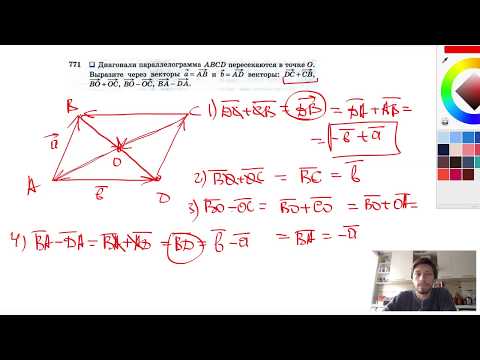
№771. В параллелограмме ABCD диагонали пересекаются в точке ОСкачать

Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Сложение векторов. 9 класс.Скачать

Угол между векторами. 9 класс.Скачать