Как находить вектор нормали плоскости

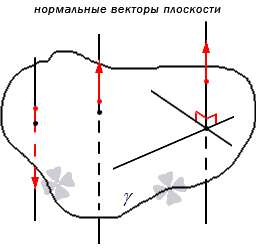
Существует ряд заданий, которым для решения необходимо нормальный вектор на плоскости, чем саму плоскость. Поэтому в этой статье получим ответ на вопрос определения нормального вектора с примерами и наглядными рисунками. Определим векторы трехмерного пространства и плоскости по уравнениям.

Видео:Репетитор по математике ищет нормаль к плоскостиСкачать

Нормальный вектор плоскости – определение, примеры, иллюстрации

Чтобы материал легко усваивался, необходимо предварительно изучить теорию о прямой в пространстве и представление ее на плоскости и векторы.

Нормальным вектором плоскости считается любой ненулевой вектор, который лежит на перпендикулярной к данной плоскости прямой.

Отсюда следует, что имеет место существование большого количества нормальных векторов в данной плоскости. Рассмотрим на рисунке, приведенном ниже.

Нормальные векторы располагаются на параллельных прямых, поэтому они все коллинеарны. То есть, при нормальном векторе n → , расположенном в плоскости γ , вектор t · n → , имея ненулевое значение параметра t , также нормальный вектор плоскости γ . Любой вектор может быть рассмотрен как направляющий вектор прямой, которая перпендикулярна этой плоскости.

Имеются случаи совпадения нормальных векторов плоскостей из-за перпендикулярности одной из параллельных плоскостей, так как прямая перпендикулярна и второй плоскости. Отсюда следует, что нормальные векторы перпендикулярных плоскостей должны быть перпендикулярными.

Рассмотрим на примере нормального вектора на плоскости.

Задана прямоугольная система координат О х у z в трехмерном пространстве. Координатные векторы i → , j → , k → считаются нормальными векторами плоскостей O y z , O x z и O x y . Это суждение верно, так как i → , j → , k → ненулевые и расположены на координатных прямых O x , O y и O z . Эти прямые перпендикулярны координатным плоскостям O y z , O x z и O x y .

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Координаты нормального вектора плоскости – нахождение координат нормального вектора плоскости из уравнения плоскости

Статья предназначена для того, чтобы научить находить координаты нормального вектора плоскости при известном уравнении плоскости прямоугольной системы координат О х у z . Для определения нормального вектора n → = ( A , B , C ) в плоскости необходимо наличие общего уравнения плоскости, имеющее вид A x + B y + C z + D = 0 . То есть достаточно иметь уравнение плоскости, тогда появится возможность для нахождения координат нормального вектора.

Найти координаты нормального вектора, принадлежащего плоскости 2 x — 3 y + 7 z — 11 = 0 .

По условию имеем уравнение плоскости. Необходимо обратить внимание на коэффициенты, так как они и являются координатами нормального вектора заданной плоскости. Отсюда получаем, что n → = ( 2 , — 3 , 7 ) — это нормальный вектор плоскости. Все векторы плоскости задаются при помощи формулы t · n → = 2 · t , — 3 · t , 7 · t , t является любым действительным числом не равным нулю.

Ответ: n → = ( 2 , — 3 , 7 ) .

Определить координаты направляющих векторов заданной плоскости x + 2 z — 7 = 0 .

По условию имеем, что дано неполное уравнение плоскости. Чтобы увидеть координаты, необходимо преобразовать уравнение x + 2 z — 7 = 0 к виду 1 · x + 0 · y + 2 z — 7 = 0 . Отсюда получим, что координаты нормального вектора данной плоскости равны ( 1 , 0 , 2 ) . Тогда множество векторов будет иметь такую форму записи ( t , 0 , 2 · t ) , t ∈ R , t ≠ 0 .

Ответ: ( t , 0 , 2 · t ) , t ∈ R , t ≠ 0 .

При помощи уравнения плоскости в отрезках, имеющего вид x a + y b + z c = 1 , и общего уравнения плоскости возможна запись нормального вектора этой плоскости, где координаты равны 1 a , 1 b , 1 c .

Знания о нормальном векторе позволяют с легкостью решать задачи. Часто встречающимися задачами являются задания с доказательствами параллельности или перпендикулярности плоскостей. Заметно упрощается решение задач на составление уравнений заданной плоскости. Если имеется вопрос о нахождении угла между плоскостями или между прямой и плоскостью, то формулы нормального вектора и нахождения его координат помогут в этом.

Видео:Направляющий и нормальный вектор прямой на плоскости | Векторная алгебраСкачать

Нормальный вектор плоскости

Вы будете перенаправлены на Автор24

Нормальный вектор плоскости — наиболее компактный и наглядный способ определить плоскость в трехмерной системе координат.

Вектор нормали к плоскости — любой ненулевой вектор, принадлежащий прямой, перпендикулярной к рассматриваемой плоскости. По отношению к такой прямой нормальный вектор является направляющим.

Для каждой плоскости существует бесконечное множество коллинеарных друг по отношению к другу нормальных векторов.

В качестве примера плоскостей, задаваемых нормальными векторами, можно рассматривать координатные плоскости системы координат $Oxyz$: $Oxy$, $Oxz$, $Oyz$. Для них нормальными векторами будут, векторы, направляющие оси, т.е., соответственно, $Oz$, $Oy$ и $Ox$ ($vec, vec, vec$).

Рисунок 1. Векторы в трехмерной системе координат. Автор24 — интернет-биржа студенческих работ

Рассмотрим основные математические закономерности, показываюшие как найти вектор нормали к плоскости.

Формула нормального вектора выводится из общего уравнения плоскости, которое имеет вид $Ax + By + Cz + D = 0$.

Плоскости, в уравнениях которых один из коэффициентов равен $0$, соответствуют базовым плоскостям системы координат ($Oxy, Oxz, Oyz$).

$Ax + D = 0 \ By + D = 0 \ Cz + D = 0$

описывают плоскости, параллельные $Oxy, Oxz, Oyz$ и отстоящие от них на расстояние, равное отношению свободного члена $D$ к соответствующему коэффициенту, например:

Нормальный вектор плоскости $Ax + By + Cz + D = 0$ можно выразить как $bar(A; B; C)$. Существует бесконечное множество плоскостей, перпендикулярных данному вектору. Для определения плоскости нужна еще точка на ней. Через любую точку также можно провести бесконечное количество плоскостей (их совокупность называется связкой). Нормальный вектор и точка взаимодополняют друг друга, определяя единственную плоскость.

Готовые работы на аналогичную тему

Точку на плоскости можно обозначить как $M_1(x; y; z)$. Вектор, соединяющий ее с любой другой точкой $M$ данной плоскости, при скалярном умножении на вектор нормали к плоскости $N$ дает ноль:

$overline cdot N = 0$

Переписав уравнение через проекции, получим

$overline cdot N = A(x — x_1) + B(y — y_1) + C(z — z_1) = 0$

Это дает нам возможность выводить уравнение плоскости через координаты точки и параметры нормального вектора плоскости.

Определить плоскость в пространстве можно и другими способами, например, с помощью указания координат трех ее точек, не лежащих на одной прямой, двух неколлинеарных векторов и точки и т.д. Однако форма записи с помощью нормального вектора плоскости и точки наиболее компактна. К ней другие методы задания плоскости можно привести путем алгебраических преобразований.

С помощью нормального вектора плоскости как ее определителя могут быть решены задачи на доказательство параллельности или перпендикулярности плоскостей, на составление уравнения плоскости, на нахождение угла между прямой и плоскостью, на нахождение угла между плоскостями.

Сформулируем уравнение плоскости, проходящей через точку с координатами $M(1; -2; 3)$ и перпендикулярной вектору $N = 2i + 4k$.

Для начала найдем коэффициенты, соответствующие координатам:

$A = 2 \ B = 0 \ C = 4$

Заметим, что $B = 0$ следует из того, что направляющий вектор $vec$ оси $Oy$ в исходном уравнении не упоминается.

Подставим значения в формулу:

$2(x — 1) + 0(y + 2) + 4(z — 3) = 0$

После стандартных преобразований получим ответ:

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 04 03 2022

Видео:1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

Вектор нормали: расчет и пример

Видео:Вектор нормали к поверхности поля в точкеСкачать

Содержание:

В нормальный вектор Он определяет направление, перпендикулярное рассматриваемому геометрическому объекту, который может быть, например, кривой, плоскостью или поверхностью.

Это очень полезная концепция для позиционирования движущейся частицы или какой-либо поверхности в пространстве. На следующем графике можно увидеть, как вектор нормали к произвольной кривой C:

Рассмотрим точку P на кривой C. Точка может представлять движущуюся частицу, которая движется по траектории C. Касательная линия к кривой в точке P нарисована красным.

Обратите внимание, что вектор Т касается C в каждой точке, а вектор N перпендикулярно Т y указывает на центр воображаемого круга, дуга которого является сегментом C. Векторы выделены жирным шрифтом в печатном тексте, чтобы отличать их от других не векторных величин.

Вектор Т он всегда указывает, куда движется частица, следовательно, указывает ее скорость. Вместо вектора N всегда указывает в том направлении, в котором вращается частица, отмечая, таким образом, вогнутость кривой C.

Видео:Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать

Как получить вектор нормали к плоскости?

Вектор нормали не обязательно является единичным вектором, то есть вектором с модулем 1, но если это так, он называется нормальный единичный вектор.

Во многих приложениях необходимо знать вектор нормали к плоскости вместо кривой. Этот вектор показывает ориентацию указанной плоскости в пространстве. Например, рассмотрим самолет п (желтый) рисунка:

К этой плоскости есть два нормальных вектора: п₁ Y п₂. Использование того или другого будет зависеть от контекста, в котором находится упомянутый самолет. Получить вектор нормали к плоскости очень просто, если вы знаете его уравнение:

ах + по + cz + d = 0, с участием к, б, c Y d вещественные числа.

Ну, нормальный вектор к указанной плоскости задается следующим образом:

N = а я + b j + c k

Здесь вектор N Он выражается через единичные векторы и перпендикулярно друг другу. я, j Y k, направленных по трем направлениям, определяющим пространство X и Zсм. рисунок 2 справа.

Видео:Геометрия. 9 класс. Уравнение прямой. Направляющий вектор и вектор нормали прямой /22.10.2020/Скачать

Вектор нормали из векторного произведения

Очень простая процедура нахождения вектора нормали использует свойства векторного произведения между двумя векторами.

Как известно, три разные точки, не лежащие на одной прямой, определяют плоскость Р. Теперь можно получить два вектора или Y v которые принадлежат упомянутой плоскости, имеющей эти три точки.

Когда у вас есть векторы, векторный продуктили Икс v — операция, результатом которой, в свою очередь, является вектор, который имеет свойство быть перпендикулярным плоскости, определяемой или Y v.

Известный этот вектор, он обозначается как N, и из него можно будет определить уравнение плоскости благодаря уравнению, указанному в предыдущем разделе:

N = или Икс v

На следующем рисунке показана описанная процедура:

Видео:Математика Без Ху!ни. Касательная плоскость и нормаль к поверхности.Скачать

пример

Найти уравнение плоскости, определяемой точками A (2,1,3); В (0,1,1); С (4.2.1).

Видео:Математический анализ, 33 урок, Касательная плоскость и нормаль к поверхностиСкачать

Решение

Это упражнение иллюстрирует описанную выше процедуру. Имея 3 точки, одна из них выбирается как общее начало двух векторов, которые принадлежат плоскости, определенной этими точками. Например, точка A устанавливается в качестве начала координат и строятся векторы AB Y AC.

Вектор AB — вектор, начало которого — точка A, а конец — точка B. Координаты вектора AB определяются соответственно вычитанием координат B из координат A:

AB = (0-2) я + (1-1) j + (1-3) k = -2я + 0j -2 k

Таким же образом поступаем и находим вектор AC:

AC = (4-2) я + (2-1) j + (1-3) k = 2я + j -2 k

Видео:Координаты вектора в пространстве. 11 класс.Скачать

Расчет векторного произведения AB x AC

Существует несколько процедур для нахождения векторного произведения между двумя векторами. В этом примере используется мнемоническая процедура, которая использует следующий рисунок для поиска векторных произведений между единичными векторами. я, j Y k:

Для начала следует помнить, что векторные произведения между параллельными векторами равны нулю, поэтому:

я Икс я = 0; j Икс j = 0; k Икс k = 0

А поскольку векторное произведение — это еще один вектор, перпендикулярный участвующим векторам, двигаясь в направлении красной стрелки, мы имеем:

я Икс j = k ; j Икс k = я; k Икс я = j

Если вам нужно двигаться в направлении, противоположном стрелке, добавьте знак (-):

j Икс я = – k; k Икс j = –я; я Икс k = –j

Всего можно составить 9 векторных произведений с единичными векторами. я, j Y k, из которых 3 будут нулевыми.

AB Икс AC = (-2я + 0j -2 k) х (2я + j -2 k)= -4(я Икс я) -2(я Икс j)+4 (я Икс k)+0 (j Икс я) + 0 (j Икс j) – 0 (j Икс k) – 4 (k Икс я)-2 (k Икс j) + 4 (k Икс k) = -2k-4j-4j+2я = 2я -8j-2k

Видео:Орт вектора. Нормировать вектор. Найти единичный векторСкачать

Уравнение плоскости

Вектор N был определен с помощью предварительно рассчитанного векторного произведения:

N = 2я -8j-2k

Следовательно, a = 2, b = -8, c = -2, искомая плоскость:

ах + по + cz + d = 0 → 2x-8y-2z + d = 0

Значение d. Это легко сделать, если значения любой из имеющихся точек A, B или C подставить в уравнение плоскости. Выбор C, например:

2,4 — 8,2 — 2,1 + d = 0

Вкратце, искомая карта:

Пытливый читатель может задаться вопросом, был бы такой же результат, если бы вместо выполнения AB Икс AC они бы предпочли произвести AC Икс AB. Ответ: да, плоскость, определяемая этими тремя точками, уникальна и имеет два вектора нормали, как показано на рисунке 2.

Что касается точки, выбранной в качестве исходной точки векторов, нет проблем с выбором любого из двух других.

Видео:Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисеСкачать

Ссылки

1. Фигероа, Д. (2005). Серия: Физика для науки и техники. Том 1. Кинематика. Отредактировал Дуглас Фигероа (USB). 31-62.
2. Нахождение нормали к плоскости. Получено с: web.ma.utexas.edu.
3. Ларсон, Р. (1986). Исчисление и аналитическая геометрия. Мак Гроу Хилл. 616-647.
4. Линии и плоскости в R 3. Получено с: math.harvard.edu.
5. Нормальный вектор. Получено с сайта mathworld.wolfram.com.

Политическая философия: история, объект исследования, проблемы

Переменные для понимания членовредительства у подростков

📽️ Видео

Уравнение плоскости через 2 точки параллельно векторуСкачать

Аналитическая геометрия, 1 урок, Векторы в пространствеСкачать

Координаты вектора. 9 класс.Скачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

5. Нормальное уравнение плоскости выводСкачать

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Метод координат Урок №2 2 Нахождение уравнения плоскости по трем точкамСкачать