Часто при изображении на чертеже контура детали приходится выполнять плавный переход одной линии в другую (плавный переход между прямыми линиями или окружностями) для выполнения конструктивных и технологических требований. Плавный переход одной линии в другую называют сопряжением.
Для построения сопряжений необходимо определить:
- • центры сопряжений (центры, из которых проводят дуги);
- • точки касания/точки сопряжения (точки, в которых одна линия переходит в другую);
- • радиус сопряжения (если он нс задан).
Рассмотрим основные типы сопряжений.
- Сопряжение (касание) прямой и окружности
- Касательная к окружности
- Свойство касательной
- Теорема, обратная теореме о свойстве касательной
- Построение касательной к окружности
- Сопряжения в инженерной графике на чертежах с примерами
- Сопряжение двух пересекающихся прямых линий
- Сопряжения прямой с окружностью
- Сопряжение двух окружностей
- Построение касательных
- 📸 Видео
Видео:Сопряжение прямой с окружностьюСкачать

Сопряжение (касание) прямой и окружности
Построение прямой, касательной к окружности. При построении сопряжения прямой и окружности используется известный признак касания этих линий: прямая, касательная к окружности, составляет прямой угол с радиусом, проведенным в точку касания (рис. 1.12).
Рис. 1.12. Касание прямой и окружности:
К — точка касания
Для проведения касательной к окружности через точку Л, лежащую вне окружности, необходимо:
- 1) соединить заданную точку А (рис. 1.13) с центром окружности О;
- 2) отрезок ОА разделить пополам (ОС = СА, см. рис. 1.7) и провести вспомогательную окружность радиусом СО (или СА);
Рис. 1.13. Построение касательной прямой к окружности
3) точку /С, (или К.» поскольку задача имеет два решения) соединить с точкой А.
Линия АК^ (или АК.,) является касательной к заданной окружности. Точки Ki и К2— точки касания.
Следует отметить, что рис. 1.13 иллюстрирует также один из способов точного графического построения двух перпендикулярных прямых (касательной и радиуса).
Построение прямой, касательной к двум окружностям. Обращаем внимание читателя на то, что задачу построения прямой, касательной к двум окружностям, можно рассматривать как обобщенный случай предыдущей задачи (построение касательной из точки к окружности). Сходство этих задач прослеживается из рис. 1.13 и 1.14.
Внешнее касание двух окружностей. При внешнем касании (см. рис. 1.14) обе окружности лежат но одну сторону от прямой.
На рис. 1.14 изображены малая окружность радиусом R с центром в точке А и большая окружность радиусом R< с центром в точ-
Рис. 1.14. Построение внешней касательной к двум окружностям ке О. Чтобы построить внешнюю касательную к этим окружностям, необходимо выполнить следующие действия:
- 1) через центр О большей окружности провести вспомогательную окружность радиусом (/?, — R);
- 2) построить касательные к вспомогательной окружности из точки А (центр малой окружности). Точки К< и К., — точки касания прямых и окружности (заметим, что задача имеет два решения);
- 3) точки К< и К2 соединить с центром О и продолжить эти линии до пересечения с окружностью радиусом Rv Точки пересечения Кли /С, являются точками касания (сопряжения);
- 4) через точку А провести радиусы, параллельные линиям ()КЛи ОКг Точки пересечения этих радиусов с малой окружностью — точки К-и Кл являются точками касания (сопряжения);
- 5) соединив точки Кл и /С(;, а также Кл и К5, получить искомые касательные.
Внутреннее касание двух окружностей (окружности лежат по разные стороны от прямой, рис. 1.15) выполняется по аналогии с внешнем касанием, с той лишь разницей, что через центр О большей окружности проводится вспомогательная окружность радиусом /?, + R. Па рис. 1.15 изображено два возможных решения задачи.
Рис. 1.1 5. Построение внутренней касательной к двум окружностям
Сопряжение пересекающихся прямых дугой окружности заданным радиусом. Построение (рис. 1.16) сводится к построению окружности радиусом R, касающейся одновременно обеих заданных линий.
Для нахождения центра этой окружности проводим две вспомогательные прямые, параллельные заданным, на расстоянии R от каждой из них. Точка пересечения этих прямых является центром О дуги сопряжения. Перпендикуляры, опущенные из центра О на заданные прямые, определяют точки сопряжения (касания) /С, и К2.
Рис. 1.16. Сопряжение пересекающихся прямых дугой окружности
Рис. 1.17. Построение сопряжения окружности и прямой дугой заданным радиусом R:
а — внутреннее касание; б — внешнее касание
Сопряжение окружности и прямой дугой заданным радиусом.
Примеры построения сопряжений окружности и прямой дугой заданным радиусом R приведены на рис. 1.17.
Видео:Окружность. 7 класс.Скачать

Касательная к окружности
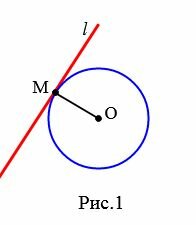
Определение 1. Прямая, которая имеет с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.
На рисунке 1 прямая l является касательной к окружности с центром O, а точка M является точкой касания прямой и окружности.
 |
Видео:Уравнение окружности (1)Скачать

Свойство касательной
Теорема 1 (Теорема о свойстве касательной). Касательная к окружности перпендикулярна к радиусу, проведенному из центра окружности к точке касания прямой и окружности.
Доказательство. Пусть l касательная к окружности с центром O и M − точка касания прямой и окружности (Рис.1). Докажем, что ( small l ⊥ OM .)
Предположим, что радиус OM является наклонной к прямой l. Поскольку перпендикуляр, проведенной из точки O к прямой l меньше наклонной OM, от центра окружности до прямой l меньше радиуса окружности. Тогда прямая l и окружность имеют две общие точки (см. статью Взаимное расположение прямой и окружности). Но касательная не может иметь с окружностью две общие точки. Получили противоречие. Следовательно прямая l пенрпендикулярна к радиусу OM.
Рассмотрим две касательные к окружности с центром O, которые проходят через точку A и касаются окружности в точках B и C (Рис.2). Отрезки AB и AC называются отрезками касательных, проведенных из точки A.
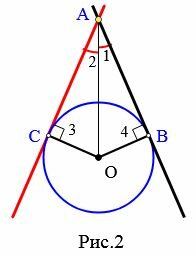 |
Теорема 2. Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через данную точку и центр окружности.
Доказательство. Рассмотрим рисунок 2. По теореме 1 касательные AC и AB перпендикулярны радиусам OC и OB, соответственно. Тогда углы 3 и 4 прямые, а треугольники ACO и ABO, прямоугольные. Эти треугольники равны по катету (OC=OB) и гипотенузе (сторона AO− общая) (подробнее см. в статье Прямоугольный треугольник. Онлайн калькулятор). Тогда AB=AC и ( small angle 1=angle 2 .) Что и требовалось доказать.
Видео:Внутреннее сопряжение дуги и прямой дугой заданного радиуса.Урок17.(Часть1.ГЕОМЕТРИЧЕСКИЕПОСТРОЕНИЯ)Скачать

Теорема, обратная теореме о свойстве касательной
Теорема 3. Если прямая проходит через конец радиуса, лежащей на окружности и перпенжикулярна к этому радиусу, то эта прямая является касательной.
Доказательство. По условию теоремы данный радиус является перпендикуляром от центра окружности к данной прямой. То есть расстояние от центра окружности до прямой равно радиусу окружности, и, следовательно, прямая и окружность имеют только одну общую точку (теорема 2 статьи Взаимное расположение прямой и окружности). Но это означает, что данная прямая является касательной к окружности (Определение 1).
Видео:Геометрия 7 класс (Урок№16 - Окружность. Задачи на построение.)Скачать

Построение касательной к окружности
Задача 1. Через точку M окружности с центром O провести касательную этой окружности (Рис.3).
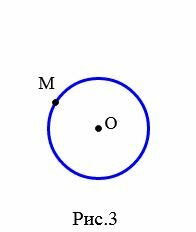 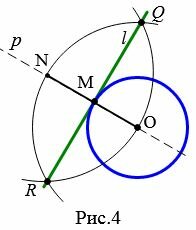 |
Решение. Проведем прямую p через точки O и M. На прямой p из точки M отложим отрезок MN равной OM. Построим две окружности с центрами O и N и одинаковыми радиусами ON. Через точки пересечения этих окружностей проведем прямую l. Полученная прямая является касательным к окружности с центром O и радиусом OM.
Задача 2. Через точку A не принадлежащая к окружности с центром O провести касательную этой окружности (Рис.5).
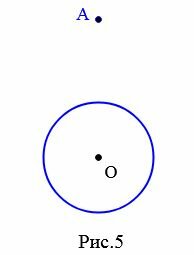 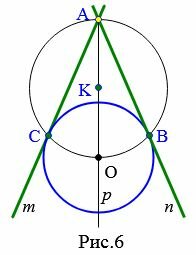 |
Решение. Проведем прямую p через точки O и A (Рис.6). Найдем среднюю точку отрезка OA и обозначим буквой K. Постоим окружность с центром K радиусом KO=KA. Найдем точки пересечения этой окружности с окружностью с центром O. Получим точки B и C. Через точки A и C проведем прямую m. Через точки A и B проведем прямую n. Прямые m и n являются касательными к окружности с центром O.
Видео:9 класс, 6 урок, Уравнение окружностиСкачать

Сопряжения в инженерной графике на чертежах с примерами
Содержание:
В очертаниях технических форм часто встречаются плавные переходы от од- ной линии к другой. Плавный переход одной линии в другую, выполненный при помощи промежуточной линии, называется сопряжением. Построение сопряжений основано на следующих положениях геометрии.
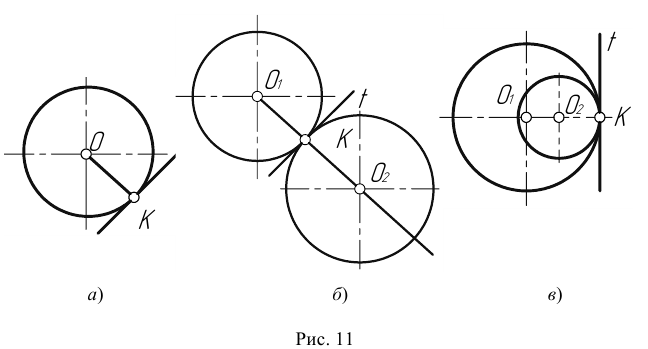
- Переход окружности в прямую будет плавным только тогда, когда заданная прямая является касательной к окружности (рис. 11а). Радиус окружности, проведенный в точку касания К, перпендикулярен к касательной прямой.
- Переход от одной окружности к другой в точке К только тогда будет плавным, когда окружности имеют в данной точке общую касательную (рис. 11б).
Точка касания К и центры окружностей
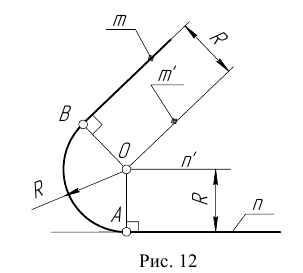
- Центром сопряжения О называется точка, равноудаленная от сопрягаемых линий (рис. 12).
- Точкой сопряжения А (В) называется точка касания двух сопрягаемых линий (рис. 12).
- Дуга сопряжения АВ – это дуга окружности, с помощью которой выполняется сопряжение (рис. 12).
- Радиус сопряжения R – это радиус дуги сопряжения (рис. 12).
Для выполнения сопряжений необходимо определить три элемента построения: 1) радиус сопряжения; 2) центр сопряжения; 3) точки сопряжения.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Сопряжение двух пересекающихся прямых линий
Пусть даны две пересекающиеся прямые m, n и радиус сопряжения R (рис. 12). Необходимо построить сопряжение данных прямых дугой окружности радиусом R.
Выполним следующие построения:
- Построим множество точек центров сопряжения, удаленных от прямой n на расстояние радиуса R сопряжения. Таким множеством является прямая
параллельная данной прямой n и отстоящая от неё на расстояние R.
- Построим множество точек центров сопряжения, удаленных от прямой m на расстояние радиуса сопряжения. Таким множеством является прямая
параллельная m и отстоящая от последней на расстояние R.
- В пересечении построенных прямых
найдем центр сопряжения О.
- Определим точку А сопряжения на прямой n. Для этого опустим из центра О перпендикуляр на прямую n . Для определения точки сопряжения В на прямой m необходимо опустить соответственно перпендикуляр из центра О на прямую m.
Проведем дугу сопряжения AB. Теперь будут определены все элементы сопряжения: радиус, центр и точки сопряжения.
Видео:1 2 4 сопряжение окружностейСкачать

Сопряжения прямой с окружностью
Сопряжение прямой с окружностью может быть внешним или внутренним. Рассмотрим построение внешнего сопряжения прямой с окружностью.
Пример 1. Пусть задана окружность радиусом R с центром в точке 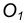
Для решения задачи выполним следующие построения:
- Построим множество точек центров сопряжения, удаленных от сопрягаемой прямой на расстояние R. Это множество задает прямая
параллельная m и отстоящая от неё на расстояние R.
- Множество точек центров сопряжения, удаленных от окружности n на рас- стояние R, есть окружность
проведенная радиусом
- Центр сопряжения О находим как точку пересечения линий
- Точку сопряжения А находим как основание перпендикуляра, проведенного из точки О на прямую m. Чтобы построить точку сопряжения В, необходимо про- вести линию центров
т.е. соединить центры сопряженных дуг. В пересечении линии центров с заданной окружностью определим точку В.
- Проведем дугу сопряжения АВ.
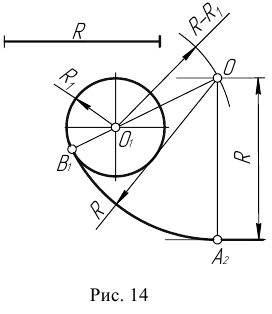
Пример 2. При построении внутреннего сопряжения (рис. 14) последовательность построений остается та же, что и в примере 1. Однако центр сопряжения определяется с помощью вспомогательной дуги окружности, проведенной из центра 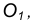
Видео:начертить окружность. Привести уравнение окружности к стандартному виду. Координаты центра и радиус.Скачать

Сопряжение двух окружностей
Сопряжение двух окружностей может быть внешним, внутренним и смешанным. Пусть задан радиус сопряжения R, а центры сопряжения и точки сопряжения следует найти.
Пример 1. Построим сопряжение с внешним касанием двух данных окружностей m и n с радиусами 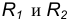
- Для нахождения центра сопряжения О проведем окружность
удаленную от данной окружности m на расстояние R . Так как сопряжение с внешним касанием, то радиус окружности
равен
- Радиусом
проведем окружность
, удаленную от данной окружности n на расстояние R.
- Найдем центр сопряжения О как точку пересечения окружностей
.
- Найдем точку сопряжения А как пересечение линии центров
с дугой m.
- Аналогично найдем точку В как пересечение линии центров
с дугой n .
- Проведем дугу сопряжения АВ.
Пример 2. Построим сопряжение с внутренним касанием двух данных окружностей m и n с радиусами 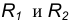
- Для нахождения центра сопряжения О проведем окружность
на расстоянии
от данной окружности m.
- Проведем окружность
на расстоянии
от данной окружности n.
- Центр сопряжения О найдем как точку пересечения окружностей
- Точку сопряжения А найдем как точку пересечения линии центров
с заданной окружностью m.
- Точку сопряжения В найдем как точку пересечения линии центров
c заданной окружностью n.
- Проведем дугу сопряжения AВ с центром в точке O.
Пример 3. На рис. 16 приведен пример построения сопряжения с внешне- внутренним касанием.
Видео:УРАВНЕНИЯ ОКРУЖНОСТИ И ПРЯМОЙ 9 класс геометрияСкачать

Построение касательных
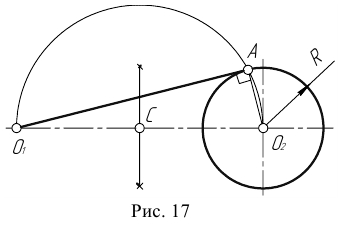
Пример 1. Дана окружность с центром в точке 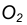
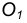
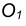
Для решения задачи выполним следующие построения.
- Соединим точку
с центром окружности
- Находим середину С отрезка
- Из точки С, как из центра, проведем вспомогательную окружность радиусом
- В точке пересечения вспомогательной окружности с заданной получим точку касания А. Соединим точку
с точкой А.
Пример 2. Построим общую касательную АВ к двум заданным окружностям радиусов 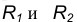
- Находим середину С отрезка
- Из точки С, как из центра, радиусом
проведем вспомогательную окружность.
- Из центра большей окружности
проведем вторую вспомогательную окружность радиусом
- Пересечение двух вспомогательных окружностей определяет точку К, через которую проходит радиус
идущий в точку касания В. 5. Для построения второй точки касания А проведем
- Соединим точки А и В отрезком прямой линии.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Нанесение размеров на чертежах
- Резьба на чертеже
- Соединения разъемные и неразъемные в инженерной графике
- Виды конструкторских документов
- Виды в инженерной графике
- Разрезы в инженерной графике
- Сечения в инженерной графике
- Выносные элементы в инженерной графике
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
📸 Видео
Окружность и круг, 6 классСкачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

ГЕОМЕТРИЯ 9 класс: Уравнение окружности и прямойСкачать

Деление окружности на 3; 6; 12 равных частейСкачать

УРАВНЕНИЕ ОКРУЖНОСТИСкачать

Построить описанную окружность (Задача 1)Скачать

Строим вписанную в данный треугольник окружность (Задача 2).Скачать

10 класс, 11 урок, Числовая окружностьСкачать

Построение окружности по трём точкам.Скачать








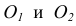
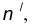 параллельная данной прямой n и отстоящая от неё на расстояние R.
параллельная данной прямой n и отстоящая от неё на расстояние R.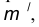 параллельная m и отстоящая от последней на расстояние R.
параллельная m и отстоящая от последней на расстояние R.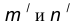 найдем центр сопряжения О.
найдем центр сопряжения О.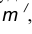 параллельная m и отстоящая от неё на расстояние R.
параллельная m и отстоящая от неё на расстояние R.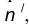 проведенная радиусом
проведенная радиусом 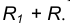
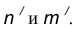
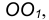 т.е. соединить центры сопряженных дуг. В пересечении линии центров с заданной окружностью определим точку В.
т.е. соединить центры сопряженных дуг. В пересечении линии центров с заданной окружностью определим точку В.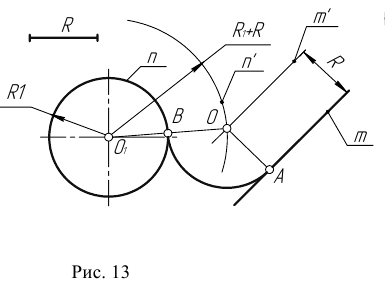
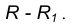
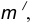 удаленную от данной окружности m на расстояние R . Так как сопряжение с внешним касанием, то радиус окружности
удаленную от данной окружности m на расстояние R . Так как сопряжение с внешним касанием, то радиус окружности 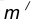 равен
равен 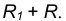
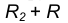 проведем окружность
проведем окружность 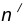 , удаленную от данной окружности n на расстояние R.
, удаленную от данной окружности n на расстояние R.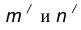 .
.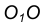 с дугой m.
с дугой m. с дугой n .
с дугой n .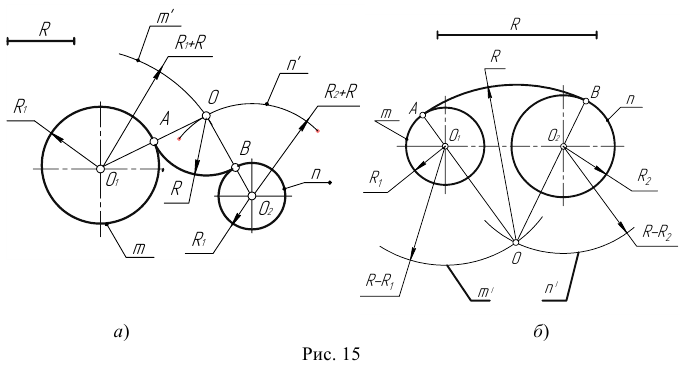
 на расстоянии
на расстоянии 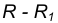 от данной окружности m.
от данной окружности m.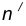 на расстоянии
на расстоянии 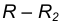 от данной окружности n.
от данной окружности n.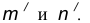
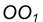 с заданной окружностью m.
с заданной окружностью m. c заданной окружностью n.
c заданной окружностью n.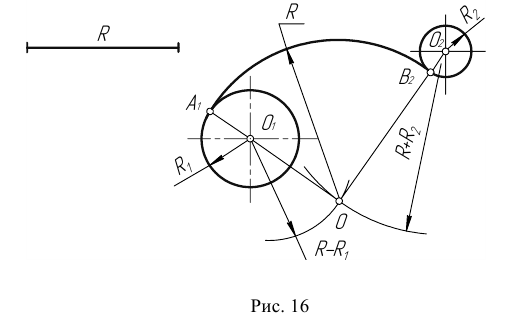
 с центром окружности
с центром окружности 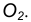
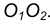
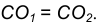
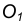 с точкой А.
с точкой А.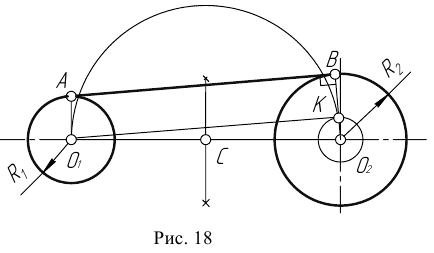
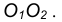
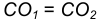 проведем вспомогательную окружность.
проведем вспомогательную окружность.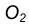 проведем вторую вспомогательную окружность радиусом
проведем вторую вспомогательную окружность радиусом 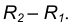
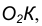 идущий в точку касания В. 5. Для построения второй точки касания А проведем
идущий в точку касания В. 5. Для построения второй точки касания А проведем