Как изображаются на чертеже параллельные прямые (5 видео)

Параллельные прямые

Две прямые называются параллельными, если они лежат на одной плоскости и не пересекаются, сколько бы их ни продолжали:

Для обозначения параллельности двух прямых используется знак || , обозначающий параллельность. Запись AB || CD (или a || b) читается так: прямая AB параллельна прямой CD (или прямая a параллельна прямой b ).

Содержание

Пересечение параллельных прямых
Построение параллельных прямых
Как изображаются на чертеже параллельные прямые
Геометрия. 7 класс
🎥 Видео

Видео:Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

Пересечение параллельных прямых

Если несколько параллельных прямых пересечь прямой линией, то эта прямая пересечёт каждую из параллельных прямых под одним и тем же углом:

Если прямые перпендикулярны одной и той же прямой, то они параллельны.

Обе прямые m и n перпендикулярны прямой a, значит прямые m и n параллельны.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Построение параллельных прямых

На свойстве пересечения прямой линией параллельных прямых основан способ их построения с помощью угольника и линейки.

Если прямая линия уже построена, то для постройки второй линии, параллельной первой, надо расположить сторону угольника вдоль построенной линии и зафиксировать это положение линейкой:

Передвинув угольник вдоль линейки, можно провести ещё одну прямую, которая будет параллельна первой.

Видео:6 .7 кл Построение параллельных прямых.Как построить параллельные прямыеСкачать

Как изображаются на чертеже параллельные прямые

Проекцией прямой, которая не перпендикулярна плоскости проекций, является прямая. Её положение определяется двумя точками, следовательно, для того чтобы построить проекцию прямой, достаточно построить проекции двух её точек.

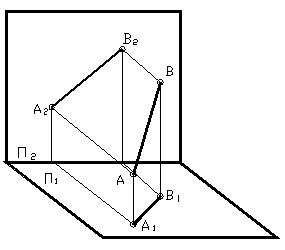
Рисунок 8

а) Прямой общего положения называется прямая, которая не параллельна и не перпендикулярна ни одной из плоскости проекций. Пример такой прямой изображён на рисунке 8. Комплексный чертёж этой прямой будет выглядеть следующим образом.

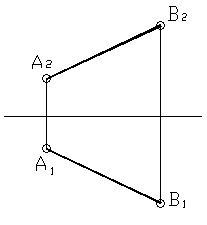
Рисунок 9

б) Прямые частного положения – это прямые, занимающие по отношению к плоскостям проекций особое положение, т.е. либо параллельные, либо перпендикулярные плоскостям проекций.

Первый подкласс прямых частного положения – прямые уровня. Это прямые, параллельные какой-либо плоскости проекций.

Горизонталь – прямая параллельная горизонтальной плоскости П1. Комплексный чертёж такой прямой изображён на рисунке 10.

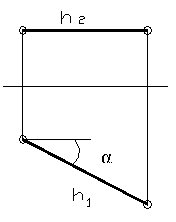
Рисунок 10

Фронтальная проекция горизонтали всегда параллельна прямой Х, а угол между осью Х и горизонтальной проекцией горизонтали составляет угол между прямой и фронтальной плоскостью проекций. Символическая запись: h // П1; α = Ð h П2.

Фронталь – прямая параллельная фронтальной плоскости П2. Комплексный чертёж фронтали изображён на рисунке 11.

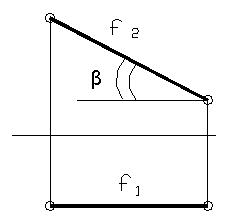
Рисунок 11

Горизонтальная проекция фронтали параллельна оси Х, а угол β — угол наклона фронтали к горизонтальной плоскости проекций; f₂ // П2, β= Ð f1 П1.

Профильная прямая – это прямая, параллельная профильной плоскости П 3 . Комплексный чертёж профильной прямой изображён на рисунке 12. Горизонтальная и фронтальная проекции профильной прямой перпендикулярны оси Х, а углы α и β — соответственно, углы наклона прямой к плоскостям П 1 и П2.

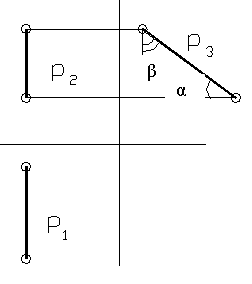
Рисунок 12.

Истинная величина прямых уровня или, так называемая натуральная величина, отображена на тех плоскостях, которым параллельны эти прямые.

Второй подкласс прямых частного положения – проецирующие прямые. Это прямые, перпендикулярные какой-либо плоскости проекций. К таким прямым относятся: горизонтально–проецирующая, фронтально-проецирующая и профильно-проецирующая прямые.

Их комплексные чертежи изображены соответственно на рисунке 13 (а, б, в).

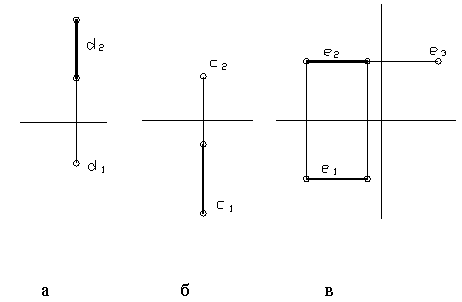
Рисунок 13

Натуральная величина горизонтально-проецирующей прямой – её фронтальная проекция, фронтально-проецирующей прямой – её горизонтальная проекция, а профильно-проецирующей прямой – её горизонтальная и фронтальная проекции.

а) три точки, не лежащие на одной прямой;

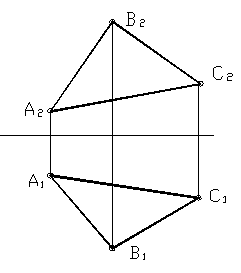
Рисунок 14

б) прямая и точка, не лежащая на ней;

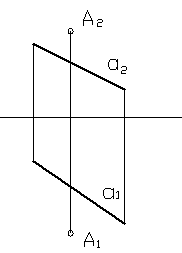
Рисунок 15

в) две параллельные прямые;

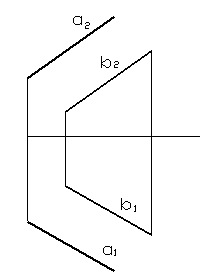
Рисунок 16

г) две пересекающиеся прямые;

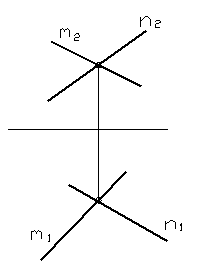
Рисунок 17

д) плоская фигура (многоугольник, круг и т.д.).

Плоскость общего положения не параллельна и не перпендикулярна ни одной из плоскостей проекций.

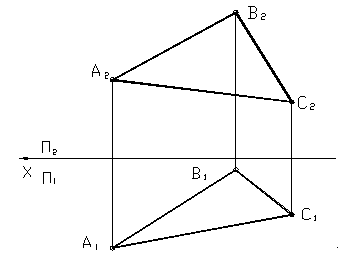
Рисунок 18

Плоскости частного положения аналогично прямой подразделяются на плоскости уровня и проецирующие плоскости. На рисунке 19 (а,б,в) изображены, соответственно, горизонтальная, фронтальная и профильная плоскости. Причём горизонтальная плоскость задана двумя параллельными прямыми, фронтальная и профильная плоскости – двумя пересекающимися прямыми.

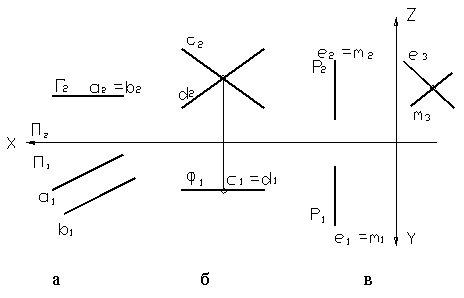
Рисунок 19

На рисунке 20 (а, б, в) показаны проецирующие плоскости. Горизонтально-проецирующая (рис. 20а) задана треугольником, фронтально-проецирующая (рис. 20б) — параллельными прямыми и профильно-проецирующая (рис. 20в) – пересекающимися прямыми.

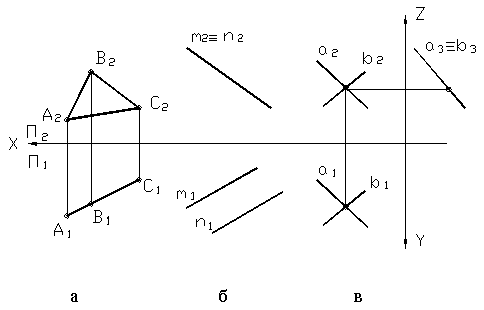
Рисунок 20

1. Как образуется комплексный чертеж прямой линии?

2. Прямые какого положения вы знаете?

3. Назовите прямые уровня.

4. Как называется прямая, проекцией которой на горизонтальной плоскости будет точка?

5. Перечислите способы задания плоскости.

6. Дайте определение плоскости общего положения.

7. Какие бывают плоскости частного положения? Как они называются и как выглядят на комплексном чертеже?

Видео:Параллельные прямые циркулемСкачать

Геометрия. 7 класс

Конспект урока

Перечень рассматриваемых вопросов:

Формулировка определения параллельных прямых.
Изображение параллельных прямых различными методами.
Как распознать на чертежах параллельные прямые?
Нахождение на рисунке пары накрест лежащих односторонних углов.

Параллельные прямые – две прямые на плоскости называются параллельными, если они не пересекаются.

Параллельные отрезки – два отрезка называются параллельными, если они лежат на параллельных прямых.

Параллельные лучи – два луча называются параллельными, если они лежат на параллельных прямых.

Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.

Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
Иченская М. А. Геометрия: Самостоятельные и контрольные работы 7–9 классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.

Теоретический материал для самостоятельного изучения.

Вы уже знаете, что на плоскости бывают пересекающиеся и непересекающиеся прямые, вы знаете, как их строить на чертеже. Теперь давайте рассмотрим прямые, которые называются параллельными, и научимся их строить различными способами.

Для начала дадим определение параллельным прямым.

Две прямые на плоскости называются параллельными, если они не пересекаются.

Параллельные прямые имеют своё обозначение: a ║ b.

Рассмотрим прямые а и b, перпендикулярные прямой c. Ранее мы выяснили, что такие прямые не пересекаются, следовательно, прямые а и b параллельны.

Очень часто рассматриваются не только параллельные прямые, но и параллельные отрезки.

Дадим им определение.

Два отрезка называются параллельными, если они лежат на параллельных прямых.

Два луча называются параллельными, если они лежат на параллельных прямых.

Рассмотрим прямую с, пересекающую прямые а и b.

Прямая c называется секущей по отношению к прямым a и b, если она пересекает каждую из них.

Как видно из рисунка, при пересечении прямых а и b секущей c образуются 8 углов. Пронумеруем полученные углы.

Оказывается, некоторые пары образованных углов имеют свои названия.

Так, например, углы 3 и 5, 4 и 6 ‑ называются накрест лежащие углы.

Углы 4 и 5 или 3 и 6 ‑ называются односторонними углами.

А пары углов 1 и 5, 4 и 8, 2 и 6 или 3 и 7 ‑ называются соответственными углами.

Как же можно построить параллельные прямые?

Для построения параллельных прямых существует несколько способов построения с помощью различных чертёжных инструментов. Рассмотрим построение параллельных прямых с помощью чертёжного угольника и линейки.

Построим прямую b, проходящую через точку M и параллельную данной прямой а.

Приложим чертёжный угольник к прямой а, к нему приложим линейку. Теперь передвинем угольник вдоль линейки так, чтобы точка M оказалась на стороне угольника, остается провести прямую b. Прямые а и b будут параллельны, на основе признаков параллельности двух прямых, которые будут изучены позднее.

Материал для углублённого изучения темы

Другие способы построения параллельных прямых.

Рассмотрим ещё два способа построения параллельных прямых с помощью чертёжных инструментов.

В чертёжной практике очень часто используется способ построения параллельных прямых с помощью рейсшины.

При выполнении столярных работ, для разметки параллельных прямых используется ещё один инструмент – малка, который представляет собой две планки, скреплённые шарниром.

При нанесении параллельных рисок можно использовать рейсмус, который представляет собой деревянную заготовку с двумя регулируемыми брусками, на концах который прикреплены для нанесения рисок иглы или гвозди.

Разбор заданий тренировочного модуля

№ 1. Один из односторонних углов при двух параллельных прямых и секущей на 40º меньше другого. Найдите меньший угол, если известно, что сумма односторонних углов равна 180°.

Пусть х – меньший из односторонних углов, тогда больший равен х + 40. Т. к. сумма односторонних углов по условию равна 180°, составим уравнение.

х = 70° – градусная мера меньшего угла.

№ 2. Через параллельные прямые а и m проведены секущие АК и КР так, как показано на рисунке. КО = ВК = АК, при этом АК = КР = 9 см, отрезок ВО =АР, АР = 6 см. На сколько сантиметров периметр ∆ВОК меньше периметра ∆АКР?