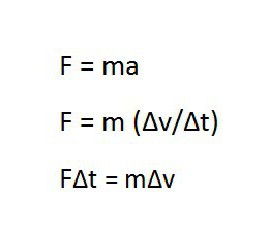Задачи по физике — это просто!
Элементарные задачи из курса школьной физики.
Векторы в физике
Многие физические величины зависят от направления и называются векторными, например, скорость, перемещение, ускорение.
При работе с векторами (векторными величинами) существуют специальные обозначения, которые надо запомнить:
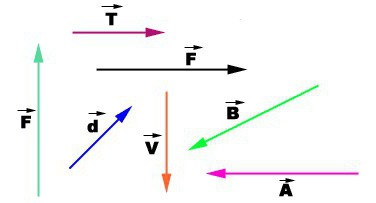
Изображение вектора на чертеже:
Если вектор параллелен координатной оси, то модуль вектора равен модулю проекции вектора на эту ось:
Проекция вектора может быть положительной или отрицательной (в зависимости от его положения относительно оси координат):
Если вектор перпендикулярен оси, то проекция вектора на эту ось равна нулю!
Как бы ни был направлен вектор, его модуль всегда можно рассчитать по формуле:
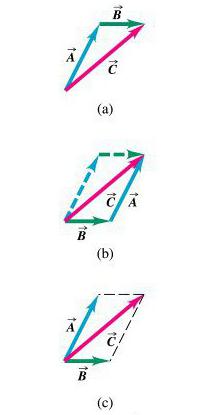
Сложение векторов (а это часто приходится выполнять в задачах) можно производить графически двумя способами — треугольника и параллелограмма.
Расчетные формулы прямолинейного равномерного движения
Расчетные формулы для прямолинейного равномерного движения — это формулы в проекциях векторов на координатную ось.
Скорость тела:

где
Vx — проекция вектора скорости на координатную ось х
Sx — проекция вектора перемещения на ось х
t — время, за которое совершается данное перемещение
Координата тела в любой момент времени
или после подстановки скорости:
Последнюю формулу иначе называют уравнением прямолинейного равномерного движения:
xo — начальная координата тела
x — конечная координата тела через время t после начала движения
Расстояние между движущимися телами при прямолинейном равномерном движении в любой момент времени:
l — расстояние между телами в любой момент времени движения
x1 — конечная координата первого тела на момент определения расстояния между телами
x2 — конечная координата второго тела на момент определения расстояния между телами
- Векторная величина в физике. Примеры векторных величин
- Как отличить скалярную величину от векторной?
- Какие действия чаще всего выполняются с векторами?
- Какие векторы изучают в физике?
- Первая величина — скорость
- Вторая величина — сила
- Третья величина — перемещение
- Четвертая величина — ускорение
- Пятая величина — импульс
- Задача о неупругом ударе
- Задача с разделением тела на части
- Задача про выстрел под углом
- Задача о переправе через реку
- Применение векторов при решении задач по физике
- 🔍 Видео
Видео:Векторы и действия над ними, проекция вектора на координатные оси. 9 класс.Скачать

Векторная величина в физике. Примеры векторных величин
Физика и математика не обходятся без понятия «векторная величина». Ее необходимо знать и узнавать, а также уметь с нею оперировать. Этому обязательно стоит научиться, чтобы не путаться и не допускать глупых ошибок.
Видео:Физика | Ликбез по векторамСкачать

Как отличить скалярную величину от векторной?
Первая всегда имеет только одну характеристику. Это ее числовое значение. Большинство скалярных величин могут принимать как положительные, так и отрицательные значения. Их примерами может служить электрический заряд, работа или температура. Но есть такие скаляры, которые не могут быть отрицательными, например, длина и масса.
Векторная величина, кроме числовой величины, которая всегда берется по модулю, характеризуется еще и направлением. Поэтому она может быть изображена графически, то есть в виде стрелки, длина которой равна модулю величины, направленной в определенную сторону.
При письме каждая векторная величина обозначается знаком стрелки на буквой. Если идет речь о числовом значении, то стрелка не пишется или ее берут по модулю.
Видео:Векторы в физике. Что нужно знать? | 50 уроков физики (2/50)Скачать

Какие действия чаще всего выполняются с векторами?
Сначала — сравнение. Они могут быть равными или нет. В первом случае их модули одинаковые. Но это не единственное условие. У них должны быть еще одинаковые или противоположные направления. В первом случае их следует называть равными векторами. Во втором они оказываются противоположными. Если не выполняется хотя бы одно из указанных условий, то векторы не равны.
Потом идет сложение. Его можно сделать по двум правилам: треугольника или параллелограмма. Первое предписывает откладывать сначала один вектор, потом от его конца второй. Результатом сложения будет тот, который нужно провести от начала первого к концу второго.
Правило параллелограмма можно использовать, когда нужно сложить векторные величины в физике. В отличие от первого правила, здесь их следует откладывать от одной точки. Потом достроить их до параллелограмма. Результатом действия следует считать диагональ параллелограмма, проведенную из той же точки.
Если векторная величина вычитается из другой, то они снова откладываются из одной точки. Только результатом будет вектор, который совпадает с тем, что отложен от конца второго к концу первого.
Видео:Урок 8. Векторные величины. Действия над векторами.Скачать

Какие векторы изучают в физике?
Их так же много, как скаляров. Можно просто запомнить то, какие векторные величины в физике существуют. Или знать признаки, по которым их можно вычислить. Тем, кто предпочитает первый вариант, пригодится такая таблица. В ней приведены основные векторные физические величины.
| Обозначение в формуле | Наименование |
| v | скорость |
| r | перемещение |
| а | ускорение |
| F | сила |
| р | импульс |
| Е | напряженность электрического поля |
| В | магнитная индукция |
| М | момент силы |
Теперь немного подробнее о некоторых из этих величин.
Видео:РАЗБИРАЕМ ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ II 😊#shorts #математика #егэ #задачи #егэ2022 #огэ2022Скачать

Первая величина — скорость
С нее стоит начать приводить примеры векторных величин. Это обусловлено тем, что ее изучают в числе первых.
Скорость определяется как характеристика движения тела в пространстве. Ею задается числовое значение и направление. Поэтому скорость является векторной величиной. К тому же ее принято разделять на виды. Первый является линейной скоростью. Ее вводят при рассмотрении прямолинейного равномерного движения. При этом она оказывается равной отношению пути, пройденного телом, ко времени движения.
Эту же формулу допустимо использовать при неравномерном движении. Только тогда она будет являться средней. Причем интервал времени, который необходимо выбирать, обязательно должен быть как можно меньше. При стремлении промежутка времени к нулю значение скорости уже является мгновенным.
Если рассматривается произвольное движение, то здесь всегда скорость — векторная величина. Ведь ее приходится раскладывать на составляющие, направленные вдоль каждого вектора, направляющего координатные прямые. К тому же определяется он как производная радиус-вектора, взятая по времени.
Видео:Зачем нужен ВЕКТОР. Объяснение смыслаСкачать

Вторая величина — сила
Она определяет меру интенсивности воздействия, которое оказывается на тело со стороны других тел или полей. Поскольку сила — векторная величина, то она обязательно имеет свое значение по модулю и направление. Так как она действует на тело, то важным является еще и точка, к которой приложена сила. Чтобы получить наглядное представление о векторах сил, можно обратиться к следующей таблице.
| Сила | Точка приложения | Направление |
| тяжести | центр тела | к центру Земли |
| всемирного тяготения | центр тела | к центру другого тела |
| упругости | место соприкосновения взаимодействующих тел | против внешнего воздействия |
| трения | между соприкасающимися поверхностями | в сторону, противоположную движению |
Также еще векторной величиной является равнодействующая сила. Она определяется как сумма всех действующих на тело механических сил. Для ее определения необходимо выполнить сложение по принципу правила треугольника. Только откладывать векторы нужно по очереди от конца предыдущего. Результатом окажется тот, который соединяет начало первого с концом последнего.
Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

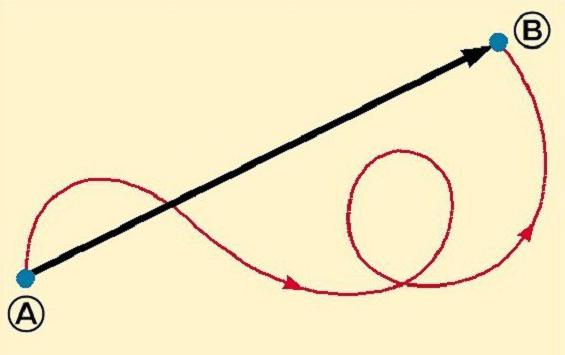
Третья величина — перемещение
Во время движения тело описывает некоторую линию. Она называется траекторией. Эта линия может быть совершенно разной. Важнее оказывается не ее внешний вид, а точки начала и конца движения. Они соединяются отрезком, который называется перемещением. Это тоже векторная величина. Причем оно всегда направлено от начала перемещения к точке, где движение было прекращено. Обозначать его принято латинской буквой r.
Здесь может появиться такой вопрос: «Путь — векторная величина?». В общем случае это утверждение не является верным. Путь равен длине траектории и не имеет определенного направления. Исключением считается ситуация, когда рассматривается прямолинейное движение в одном направлении. Тогда модуль вектора перемещения совпадает по значению с путем, и направление у них оказывается одинаковым. Поэтому при рассмотрении движения вдоль прямой без изменения направления перемещения путь можно включить в примеры векторных величин.
Видео:Построение проекции вектора на осьСкачать

Четвертая величина — ускорение
Оно является характеристикой быстроты изменения скорости. Причем ускорение может иметь как положительное, так и отрицательное значение. При прямолинейном движении оно направлено в сторону большей скорости. Если перемещение происходит по криволинейной траектории, то вектор его ускорения раскладывается на две составляющие, одна из которых направлена к центру кривизны по радиусу.
Выделяют среднее и мгновенное значение ускорения. Первое следует рассчитывать как отношение изменения скорости за некоторый промежуток времени к этому времени. При стремлении рассматриваемого интервала времени к нулю говорят о мгновенном ускорении.
Видео:Лекция 5. Сложение и вычитание векторов │ФИЗИКА С НУЛЯ теорияСкачать

Пятая величина — импульс
По-другому его еще называют количеством движения. Импульс векторной величиной является из-за того, что напрямую связан со скоростью и силой, приложенной к телу. Обе они имеют направление и задают его импульсу.
По определению последний равен произведению массы тела на скорость. Используя понятие импульса тела, можно по-другому записать известный закон Ньютона. Получается, что изменение импульса равно произведению силы на промежуток времени.
В физике важную роль имеет закон сохранения импульса, который утверждает, что в замкнутой системе тел ее суммарный импульс является постоянным.
Мы очень кратко перечислили, какие величины (векторные) изучаются в курсе физики.
Видео:➡️ КАК ВЫЧИТАТЬ ВЕКТОРЫ?Скачать

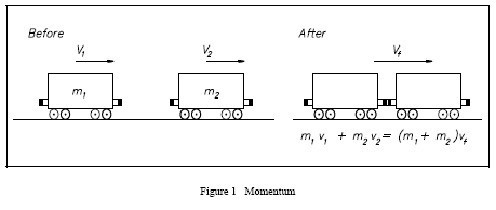
Задача о неупругом ударе
Условие. На рельсах стоит неподвижная платформа. К ней приближается вагон со скоростью 4 м/с. Массы платформы и вагона — 10 и 40 тонн соответственно. Вагон ударяется о платформу, происходит автосцеп. Необходимо вычислить скорость системы «вагон-платформа» после удара.
Решение. Сначала требуется ввести обозначения: скорость вагона до удара — v1, вагона с платформой после сцепки — v, масса вагона m1, платформы — m2. По условию задачи необходимо узнать значение скорости v.
Правила решения подобных заданий требуют схематичного изображения системы до и после взаимодействия. Ось OX разумно направить вдоль рельсов в ту сторону, куда движется вагон.
В данных условиях систему вагонов можно считать замкнутой. Это определяется тем, что внешними силами можно пренебречь. Сила тяжести и реакция опоры уравновешены, а трение о рельсы не учитывается.
Согласно закону сохранения импульса, их векторная сумма до взаимодействия вагона и платформы равна общему для сцепки после удара. Сначала платформа не двигалась, поэтому ее импульс был равен нулю. Перемещался только вагон, его импульс — произведение m1 и v1.
Так как удар был неупругий, то есть вагон сцепился с платформой, и дальше он стали катиться вместе в ту же сторону, то импульс системы не изменил направления. Но его значение стало другим. А именно произведением суммы массы вагона с платформой и искомой скорости.
Можно записать такое равенство: m1 * v1 = (m1 + m2) * v. Оно будет верно для проекции векторов импульсов на выбранную ось. Из него легко вывести равенство, которое потребуется для вычисления искомой скорости: v = m1 * v1 / (m1 + m2).
По правилам следует перевести значения для массы из тонн в килограммы. Поэтому при подстановке их в формулу следует сначала умножить известные величины на тысячу. Простые расчеты дают число 0,75 м/с.
Ответ. Скорость вагона с платформой равна 0,75 м/с.
Видео:Вычитание векторов. 9 класс.Скачать

Задача с разделением тела на части
Условие. Скорость летящей гранаты 20 м/с. Она разрывается на два осколка. Масса первого 1,8 кг. Он продолжает двигаться в направлении, в котором летела граната, со скоростью 50 м/с. Второй осколок имеет массу 1,2 кг. Какова его скорость?
Решение. Пусть массы осколков обозначены буквами m1 и m2. Их скорости соответственно будут v1 и v2. Начальная скорость гранаты — v. В задаче нужно вычислить значение v2.
Для того чтобы больший осколок продолжал двигаться в том же направлении, что и вся граната, второй должен полететь в обратную сторону. Если выбрать за направление оси то, которое было у начального импульса, то после разрыва большой осколок летит по оси, а маленький — против оси.
В этой задаче разрешено пользоваться законом сохранения импульса из-за того, что разрыв гранаты происходит мгновенно. Поэтому, несмотря на то что на гранату и ее части действует сила тяжести, она не успевает подействовать и изменить направление вектора импульса с его значением по модулю.
Сумма векторных величин импульса после разрыва гранаты равна тому, который был до него. Если записать закон сохранения импульса тела в проекции на ось OX, то он будет выглядеть так: (m1 + m2) * v = m1 * v1 — m2 * v2. Из него просто выразить искомую скорость. Она определится по формуле: v2 = ((m1 + m2) * v — m1 * v1) / m2. После подстановки числовых значений и расчетов получается 25 м/с.
Ответ. Скорость маленького осколка равна 25 м/с.
Видео:Вектор в Физике. Как Рисовать Вектор? Модуль Вектора || Урок Физики 8 класс // Подготовка к ЕГЭСкачать

Задача про выстрел под углом
Условие. На платформе массой M установлено орудие. Из него производится выстрел снарядом массой m. Он вылетает под углом α к горизонту со скоростью v (данной относительно земли). Требуется узнать значение скорости платформы после выстрела.
Решение. В этой задаче можно использовать закон сохранения импульса в проекции на ось OX. Но только в том случае, когда проекции внешних равнодействующих сил равна нулю.
За направление оси OX нужно выбрать ту сторону, куда полетит снаряд, и параллельно горизонтальной линии. В этом случае проекции сил тяжести и реакции опоры на OX будут равны нулю.
Задача будет решена в общем виде, так как нет конкретных данных для известных величин. Ответом в ней является формула.
Импульс системы до выстрела был равен нулю, поскольку платформа и снаряд были неподвижны. Пусть искомая скорость платформы будет обозначена латинской буквой u. Тогда ее импульс после выстрела определится как произведение массы на проекцию скорости. Так как платформа откатится назад (против направления оси OX), то значение импульса будет со знаком минус.
Импульс снаряда — произведение его массы на проекцию скорости на ось OX. Из-за того, что скорость направлена под углом к горизонту, ее проекция равна скорости, умноженной на косинус угла. В буквенном равенстве это будет выглядеть так: 0 = — Mu + mv * cos α. Из нее путем несложных преобразований получается формула-ответ: u = (mv * cos α) / M.
Ответ. Скорость платформы определяется по формуле u = (mv * cos α) / M.
Видео:Урок 9. Проекции вектора на координатные осиСкачать

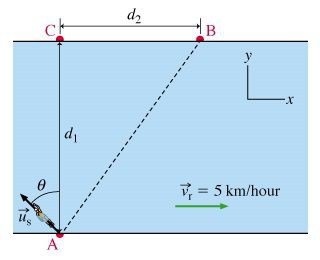
Задача о переправе через реку
Условие. Ширина реки по всей ее длине одинакова и равна l, ее берега параллельны. Известна скорость течения воды в реке v1 и собственная скорость катера v2. 1). При переправе нос катера направлен строго к противоположному берегу. На какое расстояние s его снесет вниз по течению? 2). Под каким углом α нужно направить нос катера, чтобы он достиг противоположного берега строго перпендикулярно к точке отправления? Сколько времени t потребуется на такую переправу?
Решение. 1). Полная скорость катера является векторной суммой двух величин. Первая из них течение реки, которое направлено вдоль берегов. Вторая — собственная скорость катера, перпендикулярная берегам. На чертеже получается два подобных треугольника. Первый образован шириной реки и расстоянием, на которое сносит катер. Второй — векторами скоростей.
Из них следует такая запись: s / l = v1 / v2. После преобразования получается формула для искомой величины: s = l * (v1 / v2).
2). В этом варианте задачи вектор полной скорости перпендикулярен берегам. Он равен векторной сумме v1 и v2. Синус угла, на который должен отклоняться вектор собственной скорости, равен отношению модулей v1 и v2. Для расчета времени движения потребуется разделить ширину реки на сосчитанную полную скорость. Значение последней вычисляется по теореме Пифагора.
Видео:ЛОВИ ПРОДОЛЖЕНИЕ 😉 СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ЧАСТЬ II #shorts #егэ #огэ #математика #профильныйегэСкачать

Применение векторов при решении задач по физике
Геометрический подход к решению физических задач наследуется еще от древних греков. Векторный анализ является пограничной чертой между математикой и физикой. На языке векторов формируются понимание основных законов механики и электродинамики.
На уроках физики учитель при изучении механических явлений дает определение радиус-вектора. Радиус-вектор – это направленный отрезок, проведенный из начала координат в данную точку пространства. Многие физические величины, как и радиус-вектор характеризуют и числовым значением и направлением. Например: скорость, перемещение, импульс, напряженность электрического поля, сила являются физическими векторными величинами. Длину такого вектора называют модулем вектора. Интуитивное понимание вектора у учащихся складывается с первых же уроков физики в 7 и 8 классе.
Проведем сравнение понятия вектора в физике и математике:
| В математике | В физике | |
| Изучаем векторы ( a ,b , c ) | Изучаем векторные величины ( F, v, S) | |
| Вектор можно отложить от любой точки плоскости | Вектор имеет точку приложения (на теле) | |
| Правила сложения векторов | ||
| Правило треугольника и правило параллелограмма | Чаще применяем правило параллелограмма | |
| Длину вектора называем модулем | Длину вектора называем длиной | |
Понимание вектора в физике и математике происходит поэтапно, когда ученики раскрывают и изучают следующие вопросы:
| В математике: | В физике: |
| Координатная прямая. Координатная плоскость. Координаты точки. | Понятие системы отсчета. Координаты, которыми задается положение тела на прямой, на плоскости, в пространстве, и их количество. |
| Вектор — направленный отрезок. | |
| Точка — это вектор нулевой длины или нулевой вектор. | |
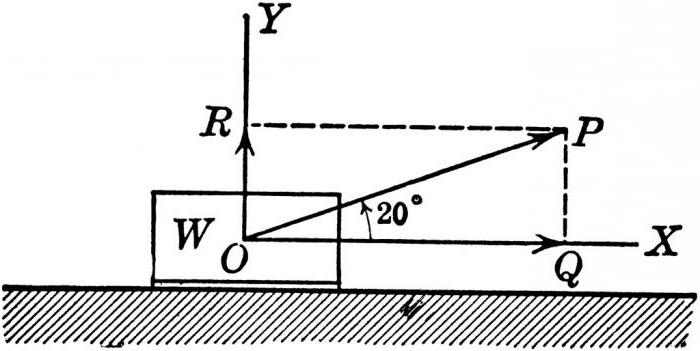
| Если от проекции начала вектора к проекции его конца надо двигаться по направлению оси, то проекция вектора на ось считают положительной. Если от проекции начала вектора к проекции его конца надо двигаться в направлении, противоположном направлению оси, то проекция отрицательная. Если вектор перпендикулярен оси координат, то проекция равна нулю. | |
| Вспомним, как связаны проекция вектора перемещения и координаты тела. (sx = х — х0, sy = y — y0) Вспомним формулы для расчета координат тела в любой момент времени (х = х0 + sx, y = y0 + sy). | |
| Операции сложения векторов. | |
| Правило треугольника. Правило многоугольника. | |
| Умножение векторов | |
| Произведение векторов (9 класс) Произведение векторов – скалярная величина. | Вычисление механической работы (10 класс): Механическая работа – скалярная величина. |
| При умножении скаляра на вектор получается вектор. |
|
| Операция проектирования | |
| Проекция ax вектора на ось X есть отрезок АВ на оси Х, где точки А и В являются основаниями перпендикуляров опущенных из начала и конца вектора на ось Х. Свойства:
| Многие задачи динамики начинаются с записи второго закона Ньютона в векторной форме. Далее переходят к его проектированию на подходящие оси. |
Учителя математики и физики должны комбинировать этот материал, разбавлять свои уроки дополнительной информацией из смежных предметов. Глубокое понимание вектора и действий с векторами у учеников сложится только посредством интеграции математического и физического определения этих понятий. Она должна быть как на уроках математики, так и на уроках физики все время, которое отводится на изучении темы «вектор».
Рассмотрим некоторые физические задачи, которые учитель математики может решить на уроках геометрии.
Задача. Парашютист со скоростью 4 м/с спускается с высоты 2 км вертикально вниз. Скорость горизонтального ветра равно 3 м/с. На какое расстояние отнесет его от места падения?
- Запишем закон сложения скоростей в векторном виде.
- Сделаем чертеж, произведя сложение векторов скоростей.
- Искомый вектор является гипотенузой прямоугольного треугольника. По теореме Пифагора вычислим её, найдя тем самым модуль скорости.
- Зная, что при прямолинейном равномерном движении модуль перемещения пропорционален скорости, составим пропорцию и найдем модуль искомого перемещения.
Следующие задачи рекомендуем рассмотреть после изучения тригонометрических функций острого угла.
Задача. Скорость лодки относительно течения 10 м/с, скорость течения 5 м/с.Под каким углом к береговой линии должен лодочник вести лодку, чтобы попасть на противоположный берег строго против того места, от которого он отплыл? Сделайте чертеж.
Задача. С какой силой F (эф) надо удерживать груз весом Р (пэ) на наклонной плоскости, чтобы он не сползал вниз?
Решение: Пусть O – центр тяжести груза, к которому приложена сила P. Разложим вектор по двум взаимно перпендикулярным направлениям. Сила перпендикулярна наклонной плоскости и не вызывает перемещения груза. Сила , удерживающая груз, должна быть равной по величине и противоположной по направлению силе. Поэтому .
Задача. Тело движется по окружности со скоростью v. Найдите модуль изменения скорости тела за четверть периода.
Решение: Пусть в начале движения в точке A скорость равна v . За четверть периода тело оказалось в точке B. Модуль скорости не изменяется и равен v. Различно направление скорости. Выполним вычитание векторов и придем к результату .
Теперь рассмотрим метод решения задач кинематики и динамики, основанный на построении так называемых векторных многоугольников перемещений, скоростей, ускорений, сил, импульсов. Рассмотрим краткие теоретические основы и некоторые методические рекомендации по возможности применения геометрических (векторных) способов решения задач кинематики и динамики в школьном курсе физики. Применение векторных способов требует знания основ тригонометрии, в частности, теорем синусов и косинусов.
Векторная запись многих уравнений физики более полно отображает соответствующие процессы, в частности в современном школьном курсе механики. Векторная форма уравнений в сочетании с соответствующими рисунками раскрывает физическую ситуацию в задаче и предопределяет ее успешное решение. Есть определенные алгоритмы решения физической задачи векторным способом.
| Кинематика |
|
| Динамика |
|
| Когда в задаче рассматривается движение нескольких тел, нужно записать второй закон Ньютона для каждого тела. При составлении уравнений нужно учесть все кинематические и динамические связи между движущимися телами. | |
Для вычислений при решении задачи чаще всего используют соответствующие уравнения в проекции на оси координат, поэтому возникает необходимость обучить учащихся преобразованию векторного уравнения в уравнения для проекций по следующему алгоритму:
- изобразить вектор графически в избранном масштабе; указать на рисунке начало координат и координатную ось;
- спроецировать на ось начальную и конечную точки вектора;
- найти длину отрезка между проекциями этих точек на ось; если можно, выразить длину отрезка через модуль вектора;
- обозначить наименьший угол между положительным направлением оси и направлением вектора; определить этот угол;
- если указанный угол острый, то приписать проекции знак “+», если нет, то приписать проекции знак “-«.
- записать в уравнении длину отрезка проекции вектора с соответствующим знаком.
Теперь решим задачи:
Задача.Тело брошено вверх перпендикулярно плоскости, наклоненной под угломαк горизонту. На каком расстоянии от места броска тело упадет на эту наклонную плоскость? Сопротивлением движения пренебречь.
Решение: Изобразим треугольник перемещений, соответствующий условию задачи и соотношению . Видим, что , откуда время движения . Тогда искомое расстояние будет .
Задача. Две частицы брошены одновременно из одной точки с одинаковыми по модулю скоростямиv: первая – вертикально вверх, вторая – горизонтально. Найдите расстояние между ними спустя время t.
Решение: Так как движение частиц происходит под действием силы тяжести, ускорения частиц одинаковы и равны g. Следовательно, относительное движение второй частицы к первой — равномерное и прямолинейное с постоянной скоростью . Тогда искомое расстояние будет равным: .
Задача. Тело брошено горизонтально со скоростью v0. Найдите скорость тела и угол отклонения через время t.
Решение: В векторной форме процесс описан так: . Проекция скорости на вертикальную и горизонтальную оси: . По теореме Пифагора получаем .
Изучая, разрабатывая и используя новый математический аппарат, физики иногда незаслуженно забывают о ранее найденных и веками эффективно служивших делу физической науки математических способах и приемах. Математика является языком физики, и свободное владение математическим аппаратом облегчает понимание физической сущности явлений и процессов.
🔍 Видео
Сложение векторов. 9 класс.Скачать

Урок 11. Решение задач на действия с векторамиСкачать

как ПРОЕЦИРОВАТЬ в Физике!Скачать

Как проецировать вектора за 1 минуту?! | ЕГЭ по физике | Саня Эбонит | 100балльный репетиторСкачать

Векторы и действия над ними, проекция вектора на координатные оси. Практическая часть. 9 класс.Скачать
Векторы для чайников (что потребуется знать при решении физических задач)Скачать