Треугольник вершина которого в центре окружности

Видео:Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

Определение

Треугольник, вписанный в окружность — это треугольник, который
находится внутри окружности и соприкасается с ней всеми тремя вершинами.

На рисунке 1 изображена окружность, описанная около
треугольника и окружность, вписанная в треугольник.

ВD = FC = AE — диаметры описанной около треугольника окружности.

O — центр вписанной в треугольник окружности.

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Формулы

Радиус вписанной окружности в треугольник

r — радиус вписанной окружности.

1. Радиус вписанной окружности в треугольник,
   если известна площадь и все стороны:

Радиус вписанной окружности в треугольник,
если известны площадь и периметр:

Радиус вписанной окружности в треугольник,
если известны полупериметр и все стороны:

Радиус описанной окружности около треугольника

R — радиус описанной окружности.

1. Радиус описанной окружности около треугольника,
   если известна одна из сторон и синус противолежащего стороне угла:

Радиус описанной окружности около треугольника,
если известны все стороны и площадь:

Радиус описанной окружности около треугольника,
если известны все стороны и полупериметр:

Площадь треугольника

S — площадь треугольника.

1. Площадь треугольника вписанного в окружность,
   если известен полупериметр и радиус вписанной окружности:

Площадь треугольника вписанного в окружность,
если известен полупериметр:

Площадь треугольника вписанного в окружность,
если известен высота и основание:

Площадь треугольника вписанного в окружность,
если известна сторона и два прилежащих к ней угла:

Площадь треугольника вписанного в окружность,
если известны две стороны и синус угла между ними:

[ S = fracab cdot sin angle C ]

Периметр треугольника

P — периметр треугольника.

1. Периметр треугольника вписанного в окружность,
   если известны все стороны:
   

Периметр треугольника вписанного в окружность,
если известна площадь и радиус вписанной окружности:

Периметр треугольника вписанного в окружность,
если известны две стороны и угол между ними:

Сторона треугольника

a — сторона треугольника.

1. Сторона треугольника вписанного в окружность,
   если известны две стороны и косинус угла между ними:

Сторона треугольника вписанного в
окружность, если известна сторона и два угла:

Средняя линия треугольника

l — средняя линия треугольника.

1. Средняя линия треугольника вписанного
   в окружность, если известно основание:
   

Средняя линия треугольника вписанного в окружность,
если известныдве стороны, ни одна из них не является
основанием, и косинус угламежду ними:

Высота треугольника

h — высота треугольника.

1. Высота треугольника вписанного в окружность,
   если известна площадь и основание:

Высота треугольника вписанного в окружность,
если известен сторона и синус угла прилежащего
к этой стороне, и находящегося напротив высоты:

[ h = b cdot sin alpha ]

Высота треугольника вписанного в окружность,
если известен радиус описанной окружности и
две стороны, ни одна из которых не является основанием:

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Свойства

• Центр вписанной в треугольник окружности
  находится на пересечении биссектрис.
• В треугольник, вписанный в окружность,
  можно вписать окружность, причем только одну.
• Для треугольника, вписанного в окружность,
  справедлива Теорема Синусов, Теорема Косинусов
  и Теорема Пифагора.
• Центр описанной около треугольника окружности
  находится на пересечении серединных перпендикуляров.
• Все вершины треугольника, вписанного
  в окружность, лежат на окружности.
• Сумма всех углов треугольника — 180 градусов.
• Площадь треугольника вокруг которого описана окружность, и
  треугольника, в который вписана окружность, можно найти по
  формуле Герона.

Видео:Задание 3 №27699 ЕГЭ по математикеСкачать

Доказательство

Около любого треугольника, можно
описать окружность притом только одну.

окружность и треугольник,
которые изображены на рисунке 2.

окружность описана
около треугольника.

1. Проведем серединные
   перпендикуляры — HO, FO, EO.
2. O — точка пересечения серединных
   перпендикуляров равноудалена от
   всех вершин треугольника.
3. Центр окружности — точка пересечения
   серединных перпендикуляров — около
   треугольника описана окружность — O,
   от центра окружности к вершинам можно
   провести равные отрезки — радиусы — OB, OA, OC.

окружность описана около треугольника,
что и требовалось доказать.

Подводя итог, можно сказать, что треугольник,
вписанный в окружность — это треугольник,
в котором все серединные перпендикуляры
пересекаются в одной точке, и эта точка
равноудалена от всех вершин треугольника.

Видео:Радиус описанной окружностиСкачать

Вписанные и описанные треугольники. Еще две формулы площади треугольника. Теорема синусов

Вписанный треугольник — треугольник, все вершины которого лежат на окружности. Тогда окружность называется описанной вокруг треугольника.

Очевидно, расстояние от центра описанной окружности до каждой из вершин треугольника одинаково и равно радиусу этой окружности.

Вокруг любого треугольника можно описать окружность, причем только одну.

Окружность вписана в треугольник, если она касается всех его сторон. Тогда сам треугольник будет описанным вокруг окружности. Расстояние от центра вписанной окружности до каждой из сторон треугольника равно радиусу этой окружности.

В любой треугольник можно вписать окружность, причем только одну.

Попробуйте сами описать окружность вокруг треугольника и вписать окружность в треугольник.

Как вы думаете, почему центр вписанной окружности — это точка пересечения биссектрис треугольника, а центр описанной окружности — точка пересечения серединных перпендикуляров к его сторонам?

В задачах ЕГЭ чаще всего встречаются вписанные и описанные правильные треугольники.

Есть и другие задачи. Для их решения вам понадобятся еще две формулы площади треугольника, а также теорема синусов.

Вот еще две формулы для площади.
Площадь треугольника равна половине произведения его периметра на радиус вписанной окружности.

— радиус окружности, вписанной в треугольник.

Есть и еще одна формула, применяемая в основном в задачах части :

где — стороны треугольника, — радиус описанной окружности.

Для любого треугольника верна теорема синусов:

Ты нашел то, что искал? Поделись с друзьями!

. Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен . Найдите гипотенузу c этого треугольника. В ответе укажите .

Треугольник прямоугольный и равнобедренный. Значит, его катеты одинаковы. Пусть каждый катет равен . Тогда гипотенуза равна .

Запишем площадь треугольника АВС двумя способами:

Приравняв эти выражения, получим, что . Поскольку , получаем, что . Тогда .

В ответ запишем .

. Сторона АС треугольника АВС с тупым углом В равна радиусу описанной около него окружности. Найдите угол В. Ответ дайте в градусах.

По теореме синусов,

Получаем, что . Угол — тупой. Значит, он равен .

. Боковые стороны равнобедренного треугольника равны , основание равно . Найдите радиус описанной окружности этого треугольника.

Углы треугольника не даны. Что ж, выразим его площадь двумя разными способами.

, где — высота треугольника. Ее найти несложно — ведь в равнобедренном треугольнике высота является также и медианой, то есть делит сторону пополам. По теореме Пифагора найдем . Тогда .

Задачи на вписанные и описанные треугольники особенно необходимы тем, кто нацелен на решения задания .

Видео:Изогонали угла. Радиус описанной окружности и высота, проведенные из одной вершины треугольника.Скачать

Треугольник вершина которого в центре окружности

Треугольник — фигура, состоящая из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки.

Треугольник, все три стороны которого равны, называется правильным (равносторонним) треугольником.

Пусть a, h, S, R, r — соответственно длина стороны, высота, площадь, радиус описанной и радиус вписанной окружности правильного треугольника. Тогда имеют место следующие соотношения:

Треугольник называется равнобедренным, если две его стороны равны. Равные стороны называются боковыми сторонами, а третья сторона — основанием равнобедренного треугольника. Высота, медиана и биссектриса равнобедренного треугольника, проведенные к его основанию, совпадают. Углы при основании равнобедренного треугольника равны. Высоты (медианы, биссектрисы), проведенные к боковым сторонам равнобедренного треугольника равны.

Если один из углов треугольника прямой, то треугольник называется прямоугольным. В прямоугольном треугольнике сторона, лежащая против прямого угла называется гипотенузой, а две другие стороны называются катетами этого треугольника.

Обозначим через c гипотенузу AB прямоугольного треугольника ABC, через a_c и b_c — проекции катетов a и b на гипотенузу AB, а через h_c — высоту, проведенную из вершины прямого угла C этого треугольника. Тогда имеют место следующие соотношения:

Тригонометрические функции дополнительных углов

Тригонометрические функции дополнительных углов являются сходственными:

Основное тригонометрическое тождество и следствия из него

Синусы смежных углов равны, а косинусы, тангенсы и котангенсы противоположны:

Средняя линия треугольника

Отрезок, соединяющий середины двух сторон треугольника называется средней линией треугольника. Средняя линия треугольника параллельна одной из сторон треугольника и равна ее половине. Три средние линии треугольника делят его на 4 равных треугольника.

Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника. Медианы треугольника пересекаются в одной точке, и точка пересечения делит каждую из них в отношении 2 : 1, считая от вершины.

Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника. Биссектрисы треугольника пересекаются в одной точке (центре вписанной окружности). Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника.

Перпендикуляр, опущенный из вершины треугольника, на прямую, содержащую противоположную сторону, называется высотой треугольника. Прямые, содержащие высоты треугольника, пересекаются в одной точке.

Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке (центре описанной окружности).

Квадрат стороны треугольника равен сумме квадратов двух других его сторон, уменьшенной на удвоенное произведение этих сторон на косинус угла между ними :

Видео:№213. Правильные треугольники ABC и DBC расположены так, что вершина D проектируется в центр треуголСкачать

Многоугольники

Параллелограммом называется четырехугольник, противоположные стороны которого попарно параллельны. Справедливы следующие утверждения.

— Две противоположные стороны четырехугольника равны и параллельны тогда и только тогда, когда этот четырехугольник — параллелограмм.

— Противоположные стороны четырехугольника попарно равны тогда и только тогда, когда этот четырехугольник — параллелограмм.

— Противоположные углы четырехугольника попарно равны тогда и только тогда, когда этот четырехугольник — параллелограмм.

— Диагонали четырехугольника пересекаются и точкой пересечения делятся пополам тогда и только тогда, когда этот четырехугольник — параллелограмм.

Прямоугольником называется параллелограмм, у которого все углы прямые. Так как прямоугольник, по определению, является параллелограммом, то он обладает всеми свойствами параллелограмма. Кроме того, прямоугольник обладает следующим характеристическим свойством.

Диагонали параллелограмма равны тогда и только тогда, когда этот параллелограмм — прямоугольник.

Ромбом называется параллелограмм, все стороны которого равны. Так как ромб, по определению, является параллелограммом, то он обладает всеми свойствами параллелограмма. Кроме того, ромб обладает следующими характеристическими свойствами.

Диагонали параллелограмма делят его углы пополам тогда и только тогда, когда этот параллелограмм — ромб.

Диагонали параллелограмма взаимно перпендикулярны тогда и только тогда, когда этот параллелограмм — ромб.

Середины сторон произвольного (в том числе невыпуклого или даже пространственного) четырехугольника являются вершинами параллелограмма — параллелограмма Вариньона.

Стороны этого параллелограмма параллельны соответствующим диагоналям четырехугольника.

Периметр параллелограмма Вариньона равен сумме длин диагоналей исходного четырехугольника, а площадь параллелограмма Вариньона равна половине площади исходного четырехугольника.

Если исходный параллелограмм — прямоугольник, то параллелограмм Вариньона — ромб. Если исходный параллелограмм — ромб, то параллелограмм Вариньона — прямоугольник. Если исходный параллелограмм — квадрат, то параллелограмм Вариньона — квадрат.

Трапецией называется четырехугольник, две стороны которого параллельны, а две другие не параллельны. Параллельные стороны трапеции называются ее основаниями, а две другие стороны — боковыми сторонами. Отрезок, соединяющий середины боковых сторон трапеции называется средней линией трапеции. Трапеция, боковые стороны которой равны, называется равнобедренной трапецией. Трапеция, один из углов которой прямой, равен называется прямоугольной трапецией. Трапеция обладает следующими свойствами.

— Средняя линия трапеции параллельна ее основаниям и равна их полусумме.

— Отрезок, соединяющие середины диагоналей трапеции, равен полуразности большего и меньшего оснований.

— Диагонали трапеции равны тогда и только тогда, когда эта трапеция равно-бедренная.

— Углы при каждом основании трапеции равны тогда и только тогда, когда эта трапеция равнобедренная.

— Сумма противолежащих углов в равнобедренной трапеции равна 180°.

— В равнобедренной трапеции расстояние от вершины одного основания до проекции противоположной вершины на прямую, содержащую это основание, равно средней линии.

Правильным шестиугольником называется шестиугольник, у которого все стороны и углы равны. Правильный шестиугольник обладает следующими свойствами.

— Сторона правильного шестиугольника равна радиусу описанной вокруг него окружности.

— Большая диагональ правильного шестиугольника является диаметром описанной вокруг него окружности и равна двум его сторонам.

— Меньшая диагональ правильного шестиугольника в раз больше его стороны.

— Угол между сторонами правильного шестиугольника равен 120°.

— Меньшая диагональ правильного шестиугольника перпендикулярна его стороне.

— Треугольник, образованный стороной шестиугольника, его большей и меньшей диагоналями, прямоугольный, а его острые углы равны 30° и 60°.

Теоремы о площадях многоугольников

Для вычисления площадей многоугольников применяют следующие теоремы.

Площадь треугольника равна половине произведения стороны на высоту, проведенную к этой стороне или к ее продолжению.

Площадь треугольника равна половине произведения сторон на синус угла между ними.

Площадь квадрата равна квадрату его стороны.

Площадь прямоугольника равна произведению его сторон.

Площадь параллелограмма равна произведению стороны на высоту, проведенную к этой стороне.

Площадь параллелограмма равна произведению сторон на синус угла между ними.

Площадь ромба равна половине произведения его диагоналей.

Площадь ромба равна произведению квадрата стороны на синус угла между сторонами.

Площадь трапеции равна произведению полусуммы оснований на высоту.

Площадь трапеции равна произведению средней линии на высоту.

Площади подобных многоугольников относятся как квадрат коэффициента подобия.

Площадь многоугольника, вершины которого лежат в узлах решетки, равна где В — количество узлов внутри многоугольника, а Г — количество узлов на границе многоугольника.

Видео:№194. Начертите треугольник. Через каждую вершину этого треугольника с помощью чертежногоСкачать

Окружность,круг и их элементы

Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом.

Вписанный угол измеряется половиной дуги, на которую он опирается.

Вписанный угол равен половине центрального угла, опирающегося на ту же дугу.

Вписанные углы, опирающиеся на одну и ту же дугу, равны.

Вписанный угол, опирающийся на полуокружность, — прямой.

Отношение хорды к синусу вписанного угла, который на нее опирается, равно двум радиусам (теорема синусов).

Отрезок, концы которого лежат на окружности, называется ее хордой.

Равные хорды стягивают равные дуги.

Углы, опирающиеся на одну и ту же хорду, либо равны, либо в сумме дают 180°.

Хорда, равная диаметру, из всех точек окружности видна под углом 90°.

Радиус окружности, перпендикулярный хорде, делит ее пополам.

Угол между двумя хордами равен полусумме высекаемых ими дуг:

Произведение отрезков, на которые делится хорда данной точкой, есть для данной окружности величина постоянная и равная разности квадратов радиуса окружности и расстояния от точки пересечения хорд до центра окружности:

Касательная к окружности

Прямая, имеющая с окружностью ровно одну общую точку, называется касательной к окружности. Справедливы следующие утверждения.

Отрезки касательных к окружности, проведенные из одной точки, равны.

Касательная к окружности перпендикулярна радиусу, проведенному в точку касания.

Угол между касательной и хордой, проходящей через точку касания, равен половине заключенной между ними дуги.

Угол между двумя касательными к окружности, проведенными из одной точки, равен полуразности большей и меньшей высекаемых ими дуг.

Прямая, имеющая с окружностью две общие точки, называется секущей.

Угол между касательной и секущей, проведенными из одной точки, равен полуразности большей и меньшей высекаемых ими дуг:

Пусть через данную точку, лежащую вне окружности, проведены секущая и касательная к этой окружности. Тогда произведение расстояний от данной точки до точек пересечения секущей с окружностью равно квадрату отрезка касательной с концами в данной точке и в точке касания:

Угол между секущими, проведенными из одной точки, равен полуразности большей и меньшей высекаемых ими дуг:

Если через некоторую точку, лежащую вне окружности, проведена секущая этой окружности, то произведение расстояний от данной точки до точек пересечения секущей с окружностью есть величина постоянная, равная разности квадрата расстояния от центра окружности до данной точки и квадрата радиуса этой окружности:

Круг и его элементы

Часть плоскости, ограниченная окружностью, называется кругом. Центр, радиус и диаметр окружности, ограничивающей круг, называются также центром, радиусом и диаметром круга. Любые два радиуса делят круг на две части, каждая из которых называется круговым сектором или просто сектором. Дуга, ограничивающая сектор, называется дугой сектора. Любая хорда делит круг на две части, каждая из которых называется круговым сегментом или просто сегментом.

Соотношения между элементами окружности и круга

Пусть r — радиус окружности, d — ее диаметр, C — длина окружности, S — площадь круга, — длина дуги в n градусов, — длина дуги в радиан, — площадь сектора, ограниченного дугой в n градусов, — площадь сектора, ограниченного дугой в радиан. Тогда имеют место следующие соотношения:

Окружность называется вписанной в многоугольник, если все стороны многоугольника касаются этой окружности. Многоугольник в этом случае называется описанным около окружности.

Центр окружности, вписанной в многоугольник, есть точка, равноудаленная от всех сторон этого многоугольника, — точка пересечения биссектрис углов этого многоугольника. В многоугольник можно вписать окружность и притом только одну, тогда и только тогда, когда биссектрисы его углов пересекаются в одной точке.

В любой треугольник можно вписать окружность.

В правильный многоугольник можно вписать окружность.

В четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противоположных сторон равны.

Если окружность радиуса r вписана в многоугольник, площадь которого равна S, а полупериметр равен p, то имеет место соотношение площадь описанного многоугольника равна произведению полупериметра на радиус вписанной окружности.

Если окружность вписана в правильный треугольник, то ее радиус r выражается через его сторону a по формуле

Если окружность радиуса r вписана в прямоугольный треугольник с катетами а и b и гипотенузой с, то

Если окружность вписана в квадрат, то ее радиус равен половине стороны квадрата.

Окружность называется описанной вокруг многоугольника, если все вершины многоугольника принадлежат этой окружности. Многоугольник в этом случае называется вписанным в окружность.

Центр окружности, описанной вокруг многоугольника, есть точка, равноудаленная от всех вершин этого многоугольника, — точка пересечения серединных перпендикуляров к сторонам этого многоугольника. Около многоугольника можно описать окружность и притом только одну, тогда и только тогда, когда серединные перпендикуляры к сторонам этого многоугольника пересекаются в одной точке.

Около любого треугольника можно описать окружность. Радиус описанной окружности равен отношению половины стороны к синусу противолежащего угла:

Около правильного многоугольника можно описать окружность.

Около четырехугольника можно описать окружность тогда и только тогда, когда суммы его противоположных углов равны

Около трапеции можно описать окружность тогда и только тогда, когда эта трапеция равнобедренная.

🌟 Видео

Строим вписанную в данный треугольник окружность (Задача 2).Скачать

Как разделить окружность на 3 равные части или как вписать равнобедренный треугольник в окружностьСкачать

ТРЕУГОЛЬНИК И ОКРУЖНОСТЬСкачать

№17 Лемма о трезубце | Вписанная и вневписанная окружности | Это будет на ЕГЭ 2024 по математикеСкачать

№581. Вершины треугольника ABC лежат на сфере радиуса 13 см. Найдите расстояние от центра сферы доСкачать

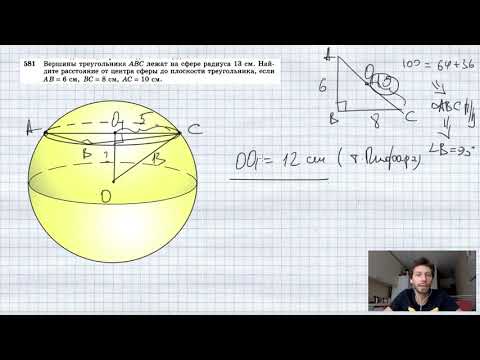
ОГЭ 2019. Задание 17. Разбор задач. Геометрия. Окружность.Скачать

Построить описанную окружность (Задача 1)Скачать

Треугольник и окружность #shortsСкачать

Три окружностиСкачать

Вписанный в окружность прямоугольный треугольник.Скачать

Описанная окружность 1. Центр окружности, описанной около треугольника.Скачать

Математика за минуту: Объяснение формулы радиуса вписанной окружности в прямоугольный треугольник.Скачать