К двум непересекающимся окружностям равных радиусов проведены две параллельные общие касательные. Окружности касаются одной из этих прямых в точках A и B Через точку C, лежащую на отрезке AB, проведены касательные к этим окружностям, пересекающие вторую прямую в точках D и E, причём отрезки CA и CD касаются одной окружности, а отрезки CB и CE — другой.
а) Докажите, что периметр треугольника CDE вдвое больше расстояния между центрами окружностей.
б) Найдите DE, если радиусы окружностей равны 5, расстояние между их центрами равно 18, а AC = 8.
а) Пусть O1 — центр окружности, которая касается отрезка CD, O2 — центр окружности, которая касается отрезка CE, R — радиус окружностей. Окружность с центром O1 касается отрезка CD в точке K, а прямой DE в точке M; окружность с центром O2 касается отрезка CE в точке L, а прямой DE в точке N (рис. 1).
Тогда периметр треугольника CDE
б) Точка O1 лежит на биссектрисах углов MDC и ACD (рис. 2), следовательно,
В прямоугольном треугольнике CO1D имеем:
Аналогично, Получаем, что
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а) при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, Содержание
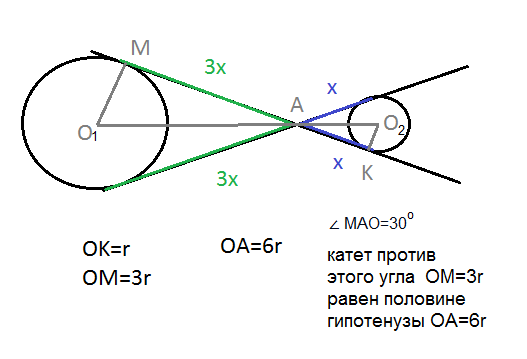
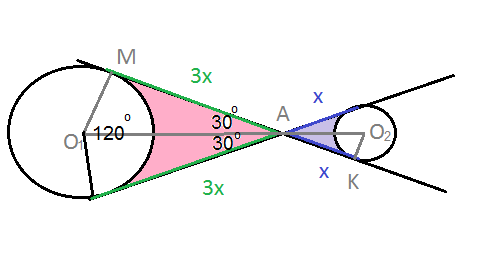
Видео:Внутренняя касательная к двум окружностямСкачать  Задача 27559 9.13. Точка пересечения двух общих.Условие9.13. Точка пересечения двух общих касательных к двум непересекающимся окружностям, меньшая из которых имеет радиус r, лежит на линии их центров на расстоянии 6r от центра большей окружности и делит отрезок касательной между точками касания в отношении 1:3. Найдите площадь фигуры, состоящей из двух частей, ограниченных касательными и большими дугами окружностей. Все решенияИз подобия треугольников МО_(1)А и КО_(2)А В прямоугольном треугольнике катет против угла в 30 градусов равен половине гипотенузы и обратно. Cм. рис. 2 S(большого круга)=Pi*(3r)^2=9Pir^2 О т в е т. 9Pir^2 + Pir^2 + (9r^2sqrt(3)-3Pir^2)+(r^2sqrt(3)-(Pir^2/3))=(20/3)Pir^2+10r^2sqrt(3) Видео:Внешняя касательная к двум окружностямСкачать  К двум непересекающимися окружностям проведены две общие внешние касательные и общая внутренняя касательная?Геометрия | 5 — 9 классы К двум непересекающимися окружностям проведены две общие внешние касательные и общая внутренняя касательная. Докажите, что отрезок внутренней касательной, заключенный между внешними касательными, равен отрезку внешней касательной, заключенному между точками касания. Для внешних касательных точки касания А и В («сверху»), А1 и В1 («снизу»), внутренняя касательная пересекает внешние в точках К (c прямой АВ) и K1 (с прямой А1В1). С — «верхняя» точка касания внутренней касательной, С1 — «нижняя». Получается вот что — одной окружности (ну, пусть слева на чертеже) касательные касаются в точках А, А1(это внешние) и С1 (это — внутренняя, как бы ниже линии центров), а другой (которая справа) — в точках В, В1(внешние) и С (внутренняя, выше линии центров). Точка К1 лежит ниже линии центров (и «слева»), и К1А1 = К1С1 ; точка К лежит выше линии центров (и «справа»), КВ = КС. СС1 = КС1 — КС = КА — КС = АВ — КВ — КС = АВ — 2 * КС. СС1 = К1С — К1С1 = К1В1 — К1С1 = А1В1 — К1С1 — А1К1 = А1В1 — 2 * К1С1 ; Но АВ = А1В1, поэтому К1С1 = КС ; АВ = КС1 + КВ = КК1 — К1С1 + КС = КК1, ч. Видео:Построение общей внешней касательной к двум окружностямСкачать  Из одной точки к окружности проведены касательная и секущая?Из одной точки к окружности проведены касательная и секущая. Касательная длиннее внутренней и внешней частей секущей на 2 и 4см. Найдите длину секущей. Видео:ПланиметрияСкачать  Две окружности имеют внешнее касание?Две окружности имеют внешнее касание. Докажите, что отрезок их внешней общей касательной , лежащий между точками касания , — среднее пропорциональное между диаметрами окружностей. Видео:Длина окружности. Площадь круга. 6 класс.Скачать  Через некоторую точку плоскости проведены касательная к окружности и секущая?Через некоторую точку плоскости проведены касательная к окружности и секущая. Внешняя часть секущей равна 3см, а внутренняя часть составляет 9см. Найдите длину касательной(касательного отрезка)». Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать  К двум окружностям с центрами в точках О1 и О 2 , касающимся внешним образом в точке А проведена общая касательная ВС(В и С точки касания)?К двум окружностям с центрами в точках О1 и О 2 , касающимся внешним образом в точке А проведена общая касательная ВС(В и С точки касания). Докажите что угол ВАС прямой. Видео:ЕГЭ 2014 математика C-4Скачать  Из внешней точки к окружности проведены секущая длиной 12 см и касательная, длина которой составляет 2 / 3 внутреннего отрезка секущей?Из внешней точки к окружности проведены секущая длиной 12 см и касательная, длина которой составляет 2 / 3 внутреннего отрезка секущей. Определите длину касательной. Видео:Геометрия 16-07. Взаимное расположение двух и более окружностей. Задача 7Скачать  К двумокружностям с центрами в точках O1O2 касающимся внешним образом вточке А, проведена общая касательная ВС (В и С — точки касания)?окружностям с центрами в точках O1 O2 касающимся внешним образом в точке А, проведена общая касательная В С (В и С — точки касания). Докажите, что угол BAC прямой. Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать  Окружности радиусами 6 и 2 касаются внешне ?Окружности радиусами 6 и 2 касаются внешне . Найдите расстояние от точки касания до общей касательной к окружностям. Видео:Отрезки касательных из одной точки до точек касания окружности равны | Окружность | ГеометрияСкачать  Две окружности касаются внешним образом?Две окружности касаются внешним образом. Их радиусы относятся как 3 : 1, а длина их общей внешней касательной равна 6. Найдите периметр фигуры, образованной внешними касательными и внешними частями окружностей. Видео:Задача про две вневписанные окружности | ЕГЭ. Задание 16. Математика | Борис Трушин |Скачать  Окружности, радиусы которых равны 4 см и 9 см, имеют внешнее касание?Окружности, радиусы которых равны 4 см и 9 см, имеют внешнее касание. К окружностям проведена общая внешняя касательная. Найдите расстояние между точками касания. Видео:Задача 6 №27922 ЕГЭ по математике. Урок 139Скачать  Окружности?Радиусы которых равны 4см и 9см, имеют внешнее касание. К окружностям проведена общая внешняя касательная. Найдите расстояние между точками касания. ( Желаельно с рисунком). Если вам необходимо получить ответ на вопрос К двум непересекающимися окружностям проведены две общие внешние касательные и общая внутренняя касательная?, относящийся к уровню подготовки учащихся 5 — 9 классов, вы открыли нужную страницу. В категории Геометрия вы также найдете ответы на похожие вопросы по интересующей теме, с помощью автоматического «умного» поиска. Если после ознакомления со всеми вариантами ответа у вас остались сомнения, или полученная информация не полностью освещает тематику, создайте свой вопрос с помощью кнопки, которая находится вверху страницы, или обсудите вопрос с посетителями этой страницы. 5у — 4х = — 1таких точек бесконечно много, подберём несколько таких : х = 1 5у — 4 = — 1 5у = 3 у = 0, 6(1 ; 0, 6) х = 1, 2 5у — 6 = — 1 5у = 5 у = 1(1, 2 ; 1). 💡 ВидеоВписанные и описанные окружности. Вебинар | МатематикаСкачать  Курс "ЕГЭ Параметры" Урок 2 "Слипшиеся окружности. Квадрат" Новиков АлександрСкачать  Задача 6 №27913 ЕГЭ по математике. Урок 131Скачать  Взаимное расположение двух окружностей. Урок 8. Геометрия 9 классСкачать  ОГЭ/БАЗА Всё, что нужно знать про окружности в ОГЭ по математикеСкачать  Вписанные углы в окружностиСкачать  Геометрия 16-09. Взаимное расположение двух и более окружностей. Задача 9Скачать  Задача 6 №27916 ЕГЭ по математике. Урок 133Скачать  |