Известно что прямая а параллельна прямой б а прямая б параллельна прямой с

305. Параллельны ли изображённые на рисунке 212 прямые a и b , если:

3) ∠ 4 = 125°, ∠ 6 = 55°;

4) ∠ 2 = 35°, ∠ 5 = 146°;

5) ∠ 1 = 98°, ∠ 6 = 82°;

6) ∠ 1 = 143°, ∠ 7 = 37°?

306. На каких из рисунков 213, а – г прямые m и n параллельны?

307. На рисунке 214 укажите все пары параллельных прямых.

308. На рисунке 215 укажите параллельные прямые, если ∠ 1 = 53°, ∠ 2 = 128°, ∠ 3 = 127°.

309. На рисунке 216 AB = BC , CD = DK . Докажите, что AB ‖ DK .

310. На рисунке 217 AK — биссектриса угла BAC , AM = MK . Докажите, что MK ‖ AC .

311. На рисунке 218 ∠ ACB = ∠ ACD , AD = CD . Докажите, что BC ‖ AD .

312. В треугольнике ABC известно, что AB = BC , ∠ A = 60°, ∠ BCD — смежный с ∠ ACB , CM — биссектриса угла BCD . Докажите, что AB ‖ CM .

313. Отрезки AB и CD пересекаются в точке O и делятся этой точкой пополам. Докажите, что AC ‖ BD .

314. На рисунке 219 AB = CD , BC = AD . Докажите, что AB ‖ CD .

315. Известно, что некоторая прямая m пересекает прямую a (рис. 220). Пересекает ли прямая m прямую b ?

316. Каково взаимное расположение прямых CD и EF на рисунке 221?

317. Угол ABC равен 60°, а угол BCD — 120°. Можно ли утверждать, что прямые AB и CD параллельны?

318. Угол между прямыми a и c равен углу между прямыми b и c . Можно ли утверждать, что прямые a и b параллельны?

319. Четыре угла, образованные при пересечении прямых a и b прямой c , равны по 40°, а любой из остальных четырёх углов — 140°. Можно ли утверждать, что прямые a и b параллельны?

320. Прямая пересекает биссектрису BM треугольника ABC в точке O , являющейся серединой отрезка BM , а сторону BC — в точке K . Докажите, что если OK ⊥ BM , то MK ‖ AB .

321. Отрезки AM и CK — медианы треугольника ABC . На продолжении отрезка AM за точку M отложен отрезок MF , а на продолжении отрезка CK за точку K — отрезок KD так, что MF = AM , KD = CK . Докажите, что точки B , D и F лежат на одной прямой.

Упражнения для повторения

322. Луч OC разбивает угол AOB на два угла так, что ∠ AOC : ∠ BOC = 3 : 5. Найдите угол между лучом OC и биссектрисой угла, смежного с углом AOB , если угол BOC на 42° больше угла AOC .

323. На рисунке 222 AB = BC , ∠ ABK = ∠ CBM . Докажите, что BM = BK .

324. Равнобедренные треугольники ABC и ADC имеют общее основание AC . Прямая BD пересекает отрезок AC в точке E . Докажите, что AE = EC .

Наблюдайте, рисуйте, конструируйте, фантазируйте

325. Приведите пример, когда общей частью (пересечением) треугольника и четырёхугольника является восьмиугольник.

Когда сделаны уроки

Пятый постулат Евклида

В § 6 вы узнали, что в качестве аксиом выбирают очевидные утверждения. Тогда почему бы, например, теоремы 1.1 и 5.1 не включить в список аксиом, ведь они тоже очевидны? Ответ на этот вопрос понятен: если какое-то утверждение можно доказать с помощью аксиом, то это утверждение — теорема, а не аксиома. С этих позиций очень поучительна история, связанная с пятым постулатом Евклида

V постулат. И чтобы всякий раз, когда прямая при пересечении с двумя другими прямыми образует с ними односторонние углы, сумма которых меньше двух прямых, эти прямые пересекались с той стороны от секущей, с которой эта сумма меньше двух прямых углов ( рис. 223 ).

Можно показать, что пятый постулат и сформулированная нами в § 13 аксиома параллельности прямых равносильны, т. е. из постулата следует аксиома и наоборот — из аксиомы следует постулат.

Более двадцати веков многие учёные пытались доказать пятый постулат, т. е. вывести его из других аксиом Евклида. Лишь в начале XIX в. несколько математиков независимо друг от друга пришли к выводу: утверждение, что через данную точку, не лежащую на данной прямой, мож но провести только одну прямую, параллельную данной , является аксиомой.

Вам может показаться, что в этом выводе ничего особенного нет: присоединяем аксиому параллельности к уже существующему списку аксиом-правил, а дальше доказываем теоремы.

Однако если в футболе добавить только одно правило, например разрешить полевым игрокам играть и руками, то мы получим совершенно новую игру.

Если пятый постулат — это правило, которое мы принимаем, а не теорема, то его можно заменить противоположным утверждением.

Так и поступил Н.И. Лобачевский. Он заменил лишь одно правило — аксиому параллельности прямых — следующим: через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, не пересекающие данную. Новая аксиома позволила построить новую геометрию — неевклидову.

Н.И. Лобачевский (1792–1856)

Выдающийся русский математик, про-

фессор Казанского университета.

С подобной идеей несколько позже выступил венгерский математик Янош Бойяи (1802–1860).

Видео:№36. Прямая с пересекает прямую а и не пересекает прямую b, параллельную прямой а.Скачать

Тест 2 Прямые в пространстве

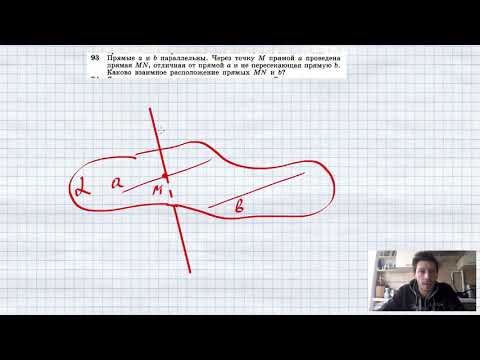
Видео:№93. Прямые а и b параллельны. Через точку М прямой a проведена прямая MN, отличная от прямой а и неСкачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»

Сертификат и скидка на обучение каждому участнику

Тест 2. «Прямые в пространстве» .

Выберите верный ответ.

1. Точка М лежит вне плоскости треугольника АВС (рис.1). Точки К, Р, Е и Н – середины отрезков МА, АС, МВ, ВС. Следовательно а) четырехугольник РКЕН является трапецией; б) четырехугольник РКЕН является параллелограммом

в) прямые КР и ЕН скрещиваются.

Если через две параллельные прямые проходят пересекающиеся плоскости, то линия их пересечения

а) параллельна каждой из двух прямых или совпадает с одной из них;

б) пересекается хотя бы с одной из этих прямых;

в) скрещивается хотя бы с одной из прямых.

3. Выясните взаимное расположение прямых АС и КС.

а) параллельны; б) определить нельзя; в) скрещиваются; г) пересекаются.

4. Каково взаимное расположение прямых AD ₁ и MN на рис. 2?

б) определить нельзя;

а) скрещиваются; б) параллельны; в) совпадают; г) пересекаются.

6. Выберите верное утверждение.

а) Две прямые называются параллельными, если они не имеют общих точек; б) две прямые, параллельные третьей прямой, параллельны;

в) две прямые, перпендикулярные третьей прямой, параллельны;

г) если углы равны, то их стороны соответственно сонаправлены.

а) прямые а и с пересекаются;

б) прямая с лежит в плоскости α ;

в) прямые а и с скрещиваются;

г) прямые а и с параллельны.

8. Каким может быть взаимное расположение прямых а и b , если через прямую а можно провести плоскость, параллельную прямой b ?

а)скрещиваются или пересекаются;

б) скрещиваются или параллельны;

в) только скрещиваются;

г) только параллельны.

9. Через вершину А параллелограмма ABCD и точку М, не лежащую в плоскости параллелограмма, проведена прямая АМ . Чему равен угол между прямыми АМ и ВС , если угол MAD равен 120˚?

а) определить нельзя; б) 120˚; в) 30˚; г) 60˚; д) 150˚.

а) 90˚; б) 45˚; в) 30˚; г) 60˚.

Тест 2. Прямые в пространстве.

Выберите верный ответ.

Точка К не лежит в плоскости треугольника АВС. Точки О; Д; Р и Е середины отрезков АС; АВ; КС и КВ соответственно(рис.1)

а) четырехугольник ОРЕД является трапецией;

б) четырехугольник ОРЕД является параллелограммом;

в) прямые ОЛ и РЕ скрещиваются

2. Если через две параллельные прямые проходят пересекающиеся плоскости, то линия их пересечения

а) параллельна каждой из двух прямых или совпадает с одной из них;

б) пересекается хотя бы с одной из этих прямых;

в) скрещивается хотя бы с одной из прямых.

а) Параллельны; б) скрещиваются; в) определить нельзя; г) пересекаются.

4. Каково взаимное расположение прямых DA ₁ и MN на рис. 2?

б) определить нельзя;

а) Определить нельзя; б) скрещиваются; в) параллельны; г) пересекаются.

6. Выберите верное утверждение.

а) если стороны двух углов соответственно сонаправлены, то углы равны;

б) две прямые, параллельные третьей прямой, пересекаются;

в) две прямые, перпендикулярные третьей прямой, перпендикулярны;

г) две прямые, имеющие общую точку, являются скрещивающимися.

а) прямые b и с пересекаются;

б) прямая b лежит в плоскости β ;

в) прямые b и с скрещиваются;

г) прямые b и с параллельны .

8. Каким может быть взаимное расположение прямых а и b , если любая плоскость, проходящая через а , не параллельна b ?

г) определить нельзя.

9. Через вершину С параллелограмма ABCD и точку М, не лежащую в плоскости параллелограмма, проведена прямая СМ . Чему равен угол между прямыми АВ и МС, если угол МС D равен 100˚?

а) 100˚; б) 80˚; в) 130˚; г) 50˚.

а) 30˚; б) 45˚; в) 60˚; г) 90˚.

Видео:№ 217 - Геометрия 7-9 класс АтанасянСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 967 человек из 79 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 342 человека из 71 региона

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 689 человек из 74 регионов

Ищем педагогов в команду «Инфоурок»

• Осипова Елена БорисовнаНаписать 8248 28.09.2020

Номер материала: ДБ-1318707

28.09.2020 0

31.07.2020 0

03.04.2020 10

24.02.2020 40

21.01.2020 72

29.10.2019 282

29.10.2019 64

12.06.2019 211

Не нашли то, что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Глава СПЧ предложил ввести подготовительные курсы перед обучением в школе для детей мигрантов

Время чтения: 1 минута

В Госдуме предложили продлить каникулы для школьников до 16 января

Время чтения: 1 минута

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Правительство направит регионам почти 92 миллиарда рублей на ремонт и оснащение школ

Время чтения: 1 минута

В Минпросвещения рассказали о формате обучения школьников после праздников

Время чтения: 1 минута

ОНФ планирует решить проблему с низкими зарплатами водителей школьных автобусов в России

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Г10(I)-3. Параллельность плоскостей. Тесты

Геометрия 10 класс. Глава I. Тест 3.

Вариант 1.

1. Выбрать верные утверждения.

1) Две плоскости называются параллельными, если они не имеют ни одной общей точки.

2) Если две плоскости пересечены третьей, то линии их пересечения параллельны.

3) Отрезки параллельных прямых, заключённые между параллельными плоскостями, равны.

A) 1; 2; 3; B) 1; 2; C) 1; 3; D) 2; 3.

2. На рисунке 1 точки: Е-середина АМ, К-середина ВМ, Р-середина СМ. Площадь треугольника ЕКР равна 24 см 2 . Найти площадь треугольника АВС.

A) 96 см 2 ; B) 64 см 2 ; C) 72 см 2 ; D) 48 см 2 .

3. Параллельные плоскости α и β пересекают стороны угла РМК в точках А, В, Е и С, как показано на рисунке 2. Известно, что МВ=2,5АМ, АЕ=18 см. Найти ВС.

A) 40 см; B) 45 см; C) 36 см; D) 42 см.

4. На рисунке 3 точки А, В и С лежат в плоскости α, точки М, Р и К в плоскости β. Отрезки АК=СМ и ВР имеют общую середину О. Величина угла АОС составляет 60°, МК=9 см. Найти АК.

A) 20 см; B) 18 см; C) 16 см; D) 12 см.

Вариант 2.

1. Выбрать верные утверждения.

1) Возможны два случая взаимного расположения плоскостей: а) две плоскости пересекаются по прямой; б) две плоскости параллельны.

2) Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.

3) Две плоскости называются параллельными, если они не пересекаются.

A) 1; 2; 3; B) 1; 2; C) 1; 3; D) 2; 3.

2. На рисунке 1 точки: Е-середина АМ, К-середина ВМ, Р-середина СМ. Площадь треугольника АВС равна 120 см 2 . Найти площадь треугольника ЕКР.

A) 60 см 2 ; B) 40 см 2 ; C) 30 см 2 ; D) 24 см 2 .

3. Параллельные плоскости α и β пересекают стороны угла РМК в точках А, В, Е и С, как показано на рисунке 2. Известно, что МС=3,5МЕ, ВС=21 см. Найти АЕ.

A) 9 см; B) 6 см; C) 7 см; D) 12 см.

4. На рисунке 3 точки А, В и С лежат в плоскости α, точки М, Р и К в плоскости β. Отрезки АК=СМ и ВР имеют общую середину О. Величина угла МОК составляет 60°, МС=24 см. Найти АС.

A) 20 см; B) 18 см; C) 16 см; D) 12 см.

Вариант 3.

1. Выбрать верные утверждения.

1) Если прямая а пересекает плоскость α, то она пересекает также любую плоскость, отличную от плоскости α.

2) Если две пересекающиеся прямые а и с плоскости α параллельны плоскости β, то плоскости α и β пересекаются.

3) Если плоскости α и β параллельны, а прямая с лежит в плоскости α, то прямая с параллельна плоскости β.

4) Через точку А, не лежащую в плоскости α можно провести плоскости, параллельные плоскости α.

A) 1; B) 2; C) 3; D) 4.

2. На рисунке 1 плоскости АВС и МКР параллельны, АМ:МО=2:5, площадь треугольника МРК равна 50 см 2 . Найти плоскость треугольника АВС.

A) 75 см 2 ; B) 100 см 2 ; C) 96 см 2 ; D) 98 см 2 .

3. Параллельные плоскости α и β пересекают стороны угла АВС в точках М, К, Р и Е как показано на рисунке 2. Известно, что ВР=3,5МР, ВМ=12,5 см, МК=25 см. Найти РЕ.

A) 35 см; B) 36 см; C) 42 см; D) 34 см.

4. На рисунке 3 точки А, В и С лежат в плоскости α, точки М, Р и К в плоскости β. Отрезки АК=СМ и ВР имеют общую середину О, АК=17 см, МК=8 см. Найти СК.

A) 25 см; B) 15 см; C) 20 см; D) 35 см.

Вариант 4.

1. Выбрать верные утверждения.

1) Если плоскости α и β параллельны, а прямая с лежит в плоскости α, то прямая с пересечёт плоскость β.

2) Если плоскости α и β параллельны плоскости γ, то плоскости α и β параллельны.

3) Если точка А не лежит в плоскости пересекающихся прямых m и n, то через неё нельзя провести плоскость, параллельную прямым m и n.

4) Если прямая а параллельна одной из двух параллельных плоскостей, то она лежит в другой плоскости.

A) 1; B) 2; C) 3; D) 4.

2. На рисунке 1 плоскости АВС и МКР параллельны, ОК:СК=7:3, площадь треугольника АВС равна 100 см 2 . Найти плоскость треугольника МРК.

A) 50 см 2 ; B) 25 см 2 ; C) 48 см 2 ; D) 49 см 2 .

3. Параллельные плоскости α и β пересекают стороны угла АВС в точках М, К, Р и Е как показано на рисунке 2. Известно, что ВЕ=2,5КЕ, ВК=4,5 см, РЕ=15 см. Найти МК.

A) 5 см; B) 6 см; C) 9 см; D) 8 см.

4. На рисунке 3 точки А, В и С лежат в плоскости α, точки М, Р и К в плоскости β. Отрезки АК=СМ и ВР имеют общую середину О. АС=7 см, АМ=24 см. Найти АК.

A) 25 см; B) 15 см; C) 20 см; D) 35 см.

1) Возможны два случая взаимного расположения плоскостей: а) две плоскости пересекаются по прямой; б) две плоскости не имеют ни одной общей точки.

2) Две плоскости называются параллельными, если они не пересекаются.

3) Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.

4) Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.

5) Отрезки параллельных прямых, заключённые между параллельными плоскостями, равны.

🔍 Видео

№186. На рисунке 106 прямые а и b пересечены прямой с. Докажите, что a||b, если: a)∠1=37°Скачать

№45. Прямая а параллельна стороне ВС параллелограмма ABCD и не лежит в плоскости параллелограмма.Скачать

№57. Прямая а параллельна одной из двух параллельных плоскостей. Докажите, что прямаяСкачать

Параллельность прямой и плоскости. 10 класс.Скачать

Параллельность прямой к плоскостиСкачать

№198. Прямые а и b перпендикулярны к прямой р, прямая с пересекает прямую а. ПересекаетСкачать

№199. Прямая р параллельна стороне АВ треугольника ABC. Докажите, что прямые ВССкачать

Параллельные прямые | Математика | TutorOnlineСкачать

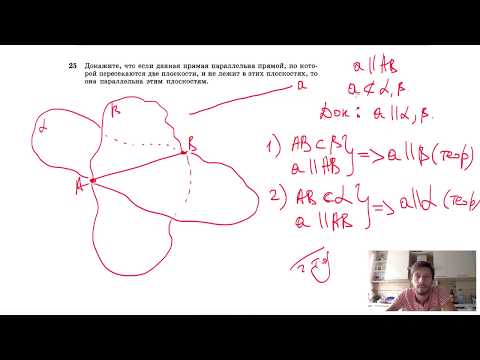
№25. Докажите, что если данная прямая параллельна прямой, по которой пересекаютсяСкачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

10 класс, 6 урок, Параллельность прямой и плоскостиСкачать

№50. Плоскости α и β параллельны, прямая m лежит в плоскости α. Докажите, что прямаяСкачать

Прямые m и n параллельны. Найдите ∠3, если ∠1=24°, ∠2=90° | ОГЭ 2017 | ЗАДАНИЕ 9 | ШКОЛА ПИФАГОРАСкачать

№16. Параллельные прямые a и b лежат в плоскости α. Докажите,Скачать

№32. Плоскости α и β пересекаются по прямой АВ. Прямая а параллельна как плоскости αСкачать

Параллельные прямые — Признак Параллельности Прямых и Свойства УгловСкачать