Формула периметра многоугольника через радиус вписанной окружности

Многоугольник (полигон) — это фигура на плоскости, которая ограничена замкнутой ломанной кривой. полигон может иметь самые разные формы или количество углов. если все углы и все стороны фигуры равны, то многоугольник считается правильным.

Формула расчёта периметра многоугольника зная длину сторон: p = a × n,
где a — длина стороны, n — количество сторон.

Формула расчёта периметра многоугольника зная радиус вписанной окружности: a = 2 × sin × (pi/n) × r,
где r — радиус вписанной окружности, дальше используем формулу расчёта периметра многоугольника.

Формула расчёта периметра многоугольника зная радиус описанной окружности: a = 2 × tg × (pi/n) × r,
где r — радиус описанной окружности, дальше используем формулу расчёта периметра многоугольника.

Видео:9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

Please wait.

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

We are checking your browser. mathvox.ru

Видео:Формулы для вычисления площади правильного многоугольника,его стороны и радиуса вписанной окружностиСкачать

Why do I have to complete a CAPTCHA?

Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.

Видео:Площадь многоугольника через радиус вписанной окружностиСкачать

What can I do to prevent this in the future?

If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.

If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.

Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.

Cloudflare Ray ID: 6d48f28219d375af • Your IP : 85.95.179.65 • Performance & security by Cloudflare

Видео:Формулы для вычисления площади правильного многоугольника,его стороны и радиуса вписанной окружностиСкачать

Правильный многоугольник

Видео:Геометрия 9 класс (Урок№22 - Формулы площади правильного многоугольника,стороны и радиуса впис.окр.)Скачать

Формулы, признаки и свойства правильного многоугольника

Многоугольником называется часть площади, которая ограничена замкнутой ломаной линией, не пересекающей сама себя.

Многоугольники отличаются между собой количеством сторон и углов.

Правильный многоугольник — это многоугольник, у которого все стороны и углы одинаковые.

Признаки правильного многоугольника

Многоугольник будет правильным, если выполняется следующее условие: все стороны и углы одинаковы.

a 1 = a 2 = a 3 = … = a n-1 = a n ,

α 1 = α 2 = α 3 = … = α n-1 = α n

где a₁ … a_n — длины сторон правильного многоугольника,
α ₁ … α _n — внутренние углы между стронами правильного многоугольника.

Основные свойства правильного многоугольника

1. Все стороны равны: a 1 = a 2 = a 3 = … = a n-1 = a n
2. Все углы равны: α 1 = α 2 = α 3 = … = α n-1 = α n
3. Центр вписанной окружности O_в совпадает с центром описанной окружности O_о, что и образуют центр многоугольникаO.
4. Сумма всех углов n-угольника равна: 180° · n — 2
5. Сумма всех внешних углов n-угольника равна 360°: β 1 + β 2 + β 3 + … + β n-1 + β n = 360°
6. Количество диагоналей (D_n) n-угольника равна половине произведения количества вершин на количество диагоналей, выходящих из каждой вершины: D n = n · n — 3 2
7. В любой многоугольник можно вписать окружность и описать круг; при этом площадь кольца, образованная этими окружностями, зависит только от длины стороны многоугольника: S = π 4 · a 2
8. Все биссектрисы углов между сторонами равны и проходят через центр правильного многоугольника O .

Видео:112. Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписаннойСкачать

Формулы правильного n-угольника

Формулы длины стороны правильного n-угольника

Формула стороны правильного n-угольника через радиус вписанной окружности

a = 2 · r · tg 180° n (через градусы),

a = 2 · r · tg π n (через радианы)

Формула стороны правильного n-угольника через радиус описанной окружности

a = 2 · R · sin 180° n (через градусы),

a = 2 · R · sin π n (через радианы)

Формулы радиуса вписанной окружности правильного n-угольника

Формула радиуса вписанной окружности n-угольника через длину стороны

r = a : 2 · tg 180° n (через градусы),

r = a : 2 · tg π n (через радианы)

Формула радиуса описанной окружности правильного n-угольника

Формула радиуса описанной окружности n-угольника через длину стороны

R = a : 2 · sin 180° n (через градусы),

R = a : 2 · sin π n (через радианы)

Формулы площади правильного n-угольника

Формула площади n-угольника через длину стороны

Формула площади n-угольника через радиус вписанной окружности

Формула площади n-угольника через радиус описанной окружности

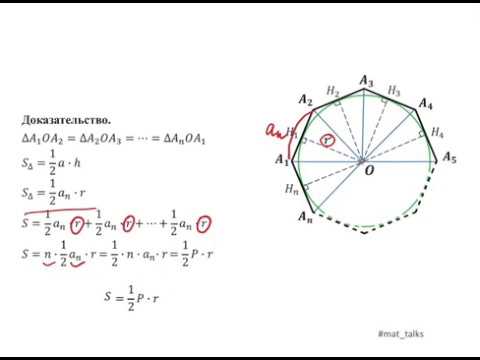
Формула периметра правильного многоугольника

Формула периметра правильного n-угольника

Периметр правильного n-угольника равен произведению длины одной стороны правильного n-угольника на количество его сторон.

Формула определения угла между сторонами правильного многоугольника

Формула угла между сторонами правильного n-угольника

Видео:Формулы радиусов описанной и вписанной окружностей правильного многоугольника 2Скачать

Правильный треугольник

Правильный треугольник — это правильный многоугольник с тремя сторонами. Все стороны правильного треугольника равны между собой, все углы также равны и составляют 60°.

Формулы правильного треугольника

Формула стороны правильного треугольника через радиус вписанной окружности

Сторона правильного треугольника равна удвоенному произведению радиуса вписанной окружности на корень из трёх.

Формула стороны правильного треугольника через радиус описанной окружности

Сторона правильного треугольника равна произведению радиуса описанной окружности на корень из трёх.

Формула площади правильного треугольника через длину стороны

Формула площади правильного треугольника через радиус вписанной окружности

Формула площади правильного треугольника через радиус описанной окружности

Углы между сторонами правильного треугольника

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Правильный четырехугольник

Правильный четырехугольник — это квадрат.

Формулы правильного четырехугольника

Формула стороны правильного четырехугольника через радиус вписанной окружности

Сторона правильного четырехугольника равна двум радиусам вписанной окружности.

Формула стороны правильного четырехугольника через радиус описанной окружности

Сторона правильного четырехугольника равна произведению радиуса описанной окружности на корень из двух.

Формула радиуса вписанной окружности правильного четырехугольника через длину стороны

Радиус вписанной окружности правильного четырехугольника равен половине стороны четырехугольника.

Формула радиуса описанной окружности правильного четырехугольника через длину стороны

Радиус описанной окружности правильного четырехугольника равен половине произведения стороны четырехугольника на корень из двух.

Формула площади правильного четырехугольника через длину стороны

Площадь правильного четырехугольника равна квадрату стороны четырехугольника.

Формула площади правильного четырехугольника через радиус вписанной окружности

Площадь правильного четырехугольника равна четырем радиусам вписанной окружности четырехугольника.

Формула площади правильного четырехугольника через радиус описанной окружности

Площадь правильного четырехугольника равна двум квадратам радиуса описанной окружности.

Углы между сторонами правильного четырехугольника

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Правильный шестиугольник

Правильный шестиугольник — это правильный многоугольник с тремя сторонами. Все стороны правильного шестиугольника равны между собой, все углы также равны и составляют 120°.

Формулы правильного шестиугольник

Формула стороны правильного шестиугольника через радиус вписанной окружности

Формула стороны правильного шестиугольника через радиус описанной окружности

Длина стороны правильного шестиугольника равна радиусу описанной окружности.

Формула радиуса вписанной окружности правильного шестиугольника через длину стороны

Формула радиуса описанной окружности правильного шестиугольника через длину стороны

Формула площади правильного шестиугольника через длину стороны

Формула площади правильного шестиугольника через радиус вписанной окружности

Формула площади правильного шестиугольника через радиус описанной окружности

Углы между сторонами правильного шестиугольника

Видео:Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

Правильный восьмиугольник

Правильный восьмиугольник — это правильный многоугольник с тремя сторонами. Все стороны правильного восьмиугольник равны между собой, все углы также равны и составляют 135°.

📸 Видео

Задача 6 №27624 ЕГЭ по математике. Урок 71Скачать

Радиус вписанной окружности, формулу через площадь и полупериметрСкачать

ГЕОМЕТРИЯ 9 класс: Формулы для вычисления площади правильного многоугольникаСкачать

Формулы для нахождения площади правильного многоугольника,его стороны и радиуса вписанной окружностиСкачать

Формулы радиуса описанной и вписанной окружности правильного многоугольника /9 класс/ СШ №1Скачать

9 класс, 22 урок, Окружность, описанная около правильного многоугольникаСкачать

Задача 6 №27934 ЕГЭ по математике. Урок 148Скачать

Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Радиус вписанной окружности #математика #егэ #математикапрофиль2023 #fyp #школаСкачать