Количество точек в треугольнике (7 видео)

Найти количество точек на или внутри треугольника для очень большого количества точек?

Вам дано N точек решетки (Xi, Yi), i = 1, 2, …, N в 2D системе координат.
Вам нужно обработать Q запросов, каждый запрос будет дан в виде «x y d».
Пусть ABC — треугольник, имеющий вершины в A (x + d, y), B (x, y) и C (x, y + d).
Для каждого запроса вы должны найти, сколько заданных точек решетки находится внутри или на границе треугольника ABC.
вход

Первая строка входных данных содержит два пробелых целых числа N и Q.
Каждая из следующих N строк содержит два целых числа Xi, разделенных пробелами, Yi, задающих координаты x и y точки решетки.
Тогда следующие Q строк содержат три пробела через целые числа x, y, d, дающие запрос.
Выход

Для каждого запроса выведите одно целое число в строке, которое обозначает количество заданных точек решетки, которые лежат внутри или на границе треугольника.
Ограничения

1 ≤ N ≤ 300000 (3 * 105)
1 ≤ Q ≤ 200000 (2 * 105)
1 ≤ Xi, Yi ≤ 300000 (3 * 105)
1 ≤ x, y, d ≤ 300000 (3 * 105)

Я получаю SIGSEGV на онлайн-судью, когда дело ввода очень большое
но работает хорошо на небольших тестовых случаях.
Куда я иду не так?

Содержание

Решение
Сколько целых точек внутри трех точек, образующих треугольник?
13 ответов
Попробуйте решить необычную задачку для первоклашек
💥 Видео

Видео:Замечательные точки треуг-ка. 8 класс.Скачать

Решение

Проверьте первую строку основной функции:

Здесь вы динамически выделяете двумерный массив X.
Теперь посмотрим на следующее ограничение:

Итак, ваша программа будет выделять X [3 * 10 ^ 5] [3 * 10 ^ 5] т.е. 9 * 10 ^ 10 массив целых чисел.
Массив такого размера слишком велик, чтобы поместиться в памяти.
В любых языках программирования такой большой объем памяти не может быть выделен / разрешен.

SIGSEGV — это ошибка (сигнал), вызванная неверной ссылкой на память или ошибкой сегментации. Вы, вероятно, пытаетесь получить доступ к элементу массива за пределами или пытаясь использовать слишком много памяти.

Итак, ваша программа сгенерирована SIGSEGV из-за слишком большой памяти.

Видео:Замечательные точки треугольника | Ботай со мной #030 | Борис Трушин ||Скачать

Сколько целых точек внутри трех точек, образующих треугольник?

на самом деле это классическая проблема, так как Виктор положите его (в другой так вопрос о каких задачах спрашивать во время интервью).

Я не мог сделать это за час (вздох) так каков алгоритм, который вычисляет количество целых точек в треугольнике?

редактировать: предположим, что вершины имеют целочисленные координаты. (в противном случае возникает проблема нахождения всех точек внутри треугольника, а затем вычитание всех плавающих точек, оставшихся только с целыми точками; менее элегантная проблема).

Видео:Пересечение двух плоскостей. Плоскости в виде треугольникаСкачать

13 ответов

предполагая, что вершины находятся в целочисленных координатах, вы можете получить ответ, построив прямоугольник вокруг треугольника, как описано в Кайле Шульце исследование теоремы пика.

для j x k прямоугольник число внутренних точек

для прямоугольника 5 x 3 ниже есть 8 внутренних точек.

для треугольников с вертикальной ногой (j) и горизонтальной ногой (k) количество внутренних точек задается

где h-количество точек внутри прямоугольника, совпадающих с гипотенузой треугольников (не длина).

для треугольников с вертикальной или горизонтальной стороной количество внутренних точек (I) задается

где j, k, h1, h2 и b отмечены на следующей диаграмме

наконец, случай треугольников без вертикальных или горизонтальных сторон можно разделить на два под-случая, один из которых область, окружающая треугольник, образует три треугольника, а другой, где окружающая область образует три треугольника и прямоугольник (см. диаграммы ниже).

количество внутренних точек (I) в первом подзапросе задается

где все переменные отмечены на следующей диаграмме

количество внутренних точек (I) во втором подзапросе задается

где все переменные отмечены на следующей диаграмме

теорема пика (http://en.wikipedia.org/wiki/Pick%27s_theorem) утверждает, что поверхность простого многоугольника, помещенного на целочисленные точки, задается:

здесь A-поверхность треугольника, i-количество внутренних точек и b-количество граничных точек. Число граничных точек b можно легко вычислить путем суммирования наибольшего общего делителя склонов каждой линии:

поверхность также может быть рассчитана. Для формулы, которая вычисляет поверхность, см. https://stackoverflow.com/a/14382692/2491535 . Комбинируя эти известные значения, я могу вычислить по:

моя реакция коленного рывка была бы грубой силой:

найдите максимальную и минимальную протяженность треугольника в направлениях x и Y.
цикл по всем комбинациям целых точек в этих экстентах.
для каждого набора точек, используйте один из стандартных тестов (та же сторона или барицентрические методы, например), чтобы увидеть, находится ли точка внутри треугольника. Поскольку этот вид вычислений является компонентом алгоритмов для обнаруживая пересечения между лучами / сегментами линий и треугольниками, вы также можете проверить этой ссылке для получения дополнительной информации.

Это называется тестом «точка в треугольнике».

здесь статьи С несколькими решениями этой проблемы:точка в тесте треугольника.

обычный способ проверить, находится ли точка в треугольнике, — это найти векторы подключение точки к каждой из трех вершин треугольника и сумма углов между этими векторами. Если сумма углов равна 2 * pi (360 градусов) тогда точка внутри треугольника, иначе это не.

Ок, я предложу один алгоритм, он не будет блестящим, но он будет работать.

во-первых, нам понадобится точка в тесте треугольник. Я предлагаю использовать «Барицентрическую технику», как объясняется в этом отличном посте:

теперь к алгоритму:

пусть (x1,y1) (x2,y2) (x3,y3) — вершины треугольника

пусть ymin = пол (min (y1, y2,y3)) ymax = потолок(max(y1,y2,y3)) xmin = пол(min(x1,x2,x3)) ymax = потолок(max(x1,x2, 3))

итерация от xmin до xmax и ymin до ymax вы можете перечислить все целочисленные точки в прямоугольной области, содержащей треугольник

используя точку в тесте треугольника, вы можете проверить для каждой точки в перечислении, чтобы увидеть, находится ли она на треугольнике.

Это просто, я думаю, что это может быть запрограммирован менее чем за полчаса.

У меня есть только половина ответа для метода без грубой силы. Если вершины были целыми, вы могли бы уменьшить его до выяснения того, как найти, сколько целых точек пересекаются ребра. С этим числом и площадью треугольника (формула Герона) вы можете использовать теорему пика, чтобы найти количество внутренних целых точек.

Edit: для другой половины, находя целочисленные точки, пересекающие ребро, я подозреваю, что это самый большой общий знаменатель между x и y разница между точками минус один, или если расстояние минус один, если одна из разностей x или y равна нулю.

вот еще один метод, не обязательно лучший, но обязательно произведет впечатление на любого интервьюера.

во-первых, назовите точку с наименьшим X co-ord ‘L’, точку с наибольшим X co-ord ‘R’ и оставшуюся точку ‘M’ (слева, справа и посередине).

затем установите два экземпляра алгоритм Bresenham по линии. Параметризуйте один экземпляр для рисования от L до R, а второй-от L до M. запустите алгоритмы одновременно для X = X[L] до X[M]. Но вместо рисуя любые линии или включая любые пиксели, подсчитайте пиксели между линиями.

после перехода от X[L] к X[M] измените параметры второго Бресенхэма для рисования от M к R, затем продолжите запускать алгоритмы одновременно для X = X[M] к X[R].

Это очень похоже на решение, предложенного Эрвином хлыщ 7 часов назад, но через Bresenham вместо линии-наклон формула.

Я думаю, что для того, чтобы подсчитать столбцы пикселей, вы будете необходимо определить, лежит ли M выше или ниже линии LR, и, конечно же, возникнут особые случаи, когда две точки имеют одинаковую координату X или Y. Но к тому времени, когда это произойдет, ваш интервьюер будет благоговеть, и вы сможете перейти к следующему вопросу.

быстрый псевдокод n’Dirty:

У меня есть идея —

пусть a(x1, y1), B(x2, y2) и C (x3, y3) — вершины треугольника. Пусть ‘count’ — количество целых точек, образующих треугольник.

Если нам нужны точки На краях треугольника, то используя формулу евклидова расстоянияhttp://en.wikipedia.org/wiki/Euclidean_distance, длину всех 3 сторон можно установить. Сумма длины всех трех сторон-3, даст этот счет.

найти номер из точек внутри треугольника нам нужно использовать алгоритм заполнения треугольника и вместо того,чтобы делать фактический рендеринг, т. е. выполнение drawpixel(x, y), просто пройдите через циклы и продолжайте обновлять счетчик, как мы делаем цикл. Алгоритм заполнения треугольника из

Основы компьютерной графики Питер Ширли, Михаил Ашихмин

принять точку верхнего треугольника (с наибольшим y координата). В этой точке начинаются два «склона». Это не общее решение, но для удобства визуализации подумайте об одном из обоих «слева» (уменьшение координат x), а другой «справа».

из этих двух склонов и любой заданной координаты Y меньше самой высокой точки, вы должны быть в состоянии вычислить количество целых точек которые появляются в пределах, установленных склонами. Итерация по убывающим координатам Y, добавьте все это количество точек вместе.

остановитесь, когда ваши убывающие координаты Y достигнут второй по высоте точки треугольника.

теперь вы подсчитали все точки «выше второй по высоте точки», и теперь у вас осталась проблема » подсчета всех точек внутри некоторых (намного меньше . ) треугольник, из которого вы знаете, что его верхняя сторона параллельна X-оси.

повторите ту же процедуру, но теперь, взяв «самую левую точку» вместо «самой верхней», и продолжая «путем увеличения x» вместо «уменьшения y».

после этого вы остаетесь с проблемой подсчета всех целых точек внутри треугольника, еще раз намного меньшего, из которых вы знаете, что его верхняя сторона параллельна оси X, а его левая сторона параллельна оси Y.

продолжайте повторять (повторяющийся), пока не посчитаете нет точки в треугольнике, с которыми вы остались.

(теперь я сделал домашнее задание для вас ?)

(wierd) псевдо-код для немного лучше, чем грубой силы(он должен иметь O (n))
надеюсь, вы понимаете, что я имею в виду.—3—>

этот алгоритм довольно легко расширить для вершин типа float (требуется только некоторый раунд В «for i..»часть, с особым случаем для P2.x-целое число (там, округлено вниз=округлено вверх))
и есть некоторые возможности для оптимизации в реальной реализации

Я нашел очень полезную ссылку, которая четко объясняет решение этой проблемы. Я слаб в координатной геометрии, поэтому я использовал это решение и закодировал его на Java, который работает (по крайней мере, для тестовых случаев, которые я пробовал..)

Видео:Где находится точка в треугольнике заданном координатами вершин, внутри или вне треугольника.Скачать

Попробуйте решить необычную задачку для первоклашек

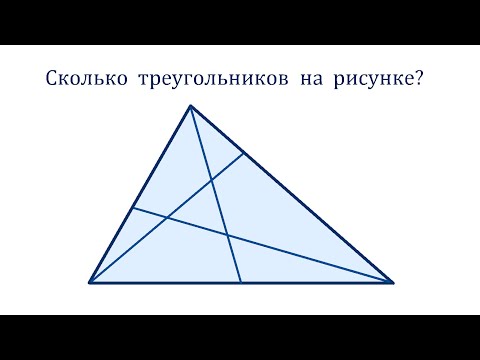
Эта банальная логическая задача стара как мир. Все очень просто: посчитайте каждый отдельный треугольник, затем сложите все различные комбинации маленьких треугольников и обязательно не забудьте про большую общую фигуру. Вы ведь так делаете? При всей своей простоте, эта задача всегда вызывает массу споров и сотни комментариев с ответами в диапазоне от четырех до 45 (боже, откуда столько?).

Давайте сначала вспомним из школьной программы, что же такое треугольник. В евклидовом пространстве это геометрическая фигура (он же многоугольник с фиксированным числом углов), образованная тремя отрезками (стороны треугольника), которые соединяют три точки (вершины треугольника), не лежащие на одной прямой. Возможно, мы повторно взорвем ваш мозг, но есть так называемый вырожденный треугольник, вершины которого таки лежат на одной прямой. Живите теперь с этим.

Отрезок, соединяющий вершину с точкой на противоположной стороне, называется чевианой. Обычно под чевианой понимают не один такой отрезок, а один из трех отрезков, проведенных из трех разных вершин треугольника и пересекающихся в одной точке. В нашем случае есть две чевианы, которые спускаются из верхнего угла на нижнюю сторону большой фигуры. Благодаря треугольнику появилась тригонометрия, планиметрия, а еще используя эту простую фигуру, люди научились составлять карты, измерять участки и конструировать. Даже «Черный квадрат» Малевича должен был называться «Черный китайский треугольник», и не спрашивайте, почему. Казимир Северинович унес эту тайну с собой на тот свет. В общем, при всей своей простоте полезная штука. Но мы отвлеклись.