Изометрия окружности в компасе (8 видео)

Построение дуги и эллипса в KOMPAS 3D

Содержание

Построение дуги окружности. Произвольная дуга, дуга по трем точкам, дуга касательная к кривой.
Построение дуги окружности. Дуга по двум точкам, дуга по двум точкам и углу раствора.
Построение эллипса.
Урок №10. Строим окружность в программе Компас 3D.
Деление окружности на любое количество равных частей в КОМПАС — 3D с примером
📺 Видео

Видео:Урок 3 ИзометрияСкачать

Построение дуги окружности. Произвольная дуга, дуга по трем точкам, дуга касательная к кривой.

Программа “Компас 3D” располагает несколькими методами, позволяющими построить дугу окружности различных типов. Включая произвольную дугу, дугу по трём точкам, дугу касательно к кривой, дугу по двум точкам, дугу по двум точкам и углу раствора. Данная статья ознакомит вас с некоторыми методами. Которые позволят получить дугу окружности.

Произвольная дуга окружности.

Для того, чтобы построить произвольную дугу, вам нужно нажать кнопку “Дуга” в панели компакта или найти её в меню сверху. Где оно скрыто за командами “Инструменты” – “Геометрия” – “Дуги” – “Дуга”.

С помощью указателя мышки вы сначала можете задать начало дуги и её центральную точку. Также вы сможете ввести положение точки начала дуги в свойственной панели. После того, как зададите размеры угла и радиуса или диаметра в нужных пунктах меню. По умолчанию задаются параметры радиуса. Итак, перейдём к постановке дуги, имеющей центр в начале координатной оси. Начальная точка указывается с учётом радиуса в 30 мм и угла в 150 градусов. После ввода данных, вам нужно будет нажать клавишу ввода или переноса.

После этого с помощью курсора или введя значение угла, вы указываете координаты точки, где будет заканчиваться дуга. Например, можем задать угол в 10 градусов.

После нажатия клавиши ввода, дуга будет строиться автоматически.

По умолчанию построение дуги заданно как построение против часовой стрелки.

Если вы желаете задать обратное направление. В панели свойств есть отдельный пункт меню, где вы сможете ввести изменения в установки по умолчанию, как на картинке выше.

Дуга по трем точкам.

Для того, чтобы построить дугу с трема точками, вам нужно нажать кнопку “Дуга по 3 точкам”. Которая находится в панели компактного меню или же сверху в меню. Где нужно последовательно нажать на пункты “Инструменты” – “Геометрия” – “Дуги” – “Дуга по 3 точкам”.

С помощью курсора мыши, вы получите возможность последовательного указания токи, где дуга будет начинаться, точки, через которую дуга должна проходить (такой точкой может быть, например, вершина прямоугольника), а также точки, в которой дуга будет заканчиваться. В данном случае система сможет самостоятельно просчитать координаты центральной точки и радиус дуги.

Дуга касательная к кривой.

Для того, чтобы построить касательную к кривой линии дугу, вам нужно нажать кнопку “Дуга касательная к кривой”. В компактной панели, или же в меню сверху, где вам предстоит нажать команды “Инструменты” – “Геометрия” – “Дуги” – “Дуга касательная к кривой”.

Вам нужно задать точку, через которую пройдёт будущая дуга, а также точку, где дуга будет заканчиваться, с помощью курсора мыши. Система способна рассчитать по умолчанию, какими будут радиус и координаты центральной точки дуги. Начало дуги будет лежать в точке соприкосновения.

После того, как вы укажете точки, экран покажет вам фантомные варианты различных возможностей и вариантов построения дуги. Вам нужно будет выбрать тот, который подходит именно вам. Далее вы должны будете зафиксировать данный вариант с помощью курсора. В завершение построения нужно нажать кнопки “Создать объект” и “Прервать команду”.

Если вы знаете радиус, предписанный касательной дуге, у вас есть возможность ввода его в нужное поле панели свойств.

К примеру, можем заняться построением дуги касательной к прямоугольнику с радиусом в 50 мм.

После того, как вы закончили ввод значений в ячейки, вам нужно нажать клавишу ввода. Экран опять покажет фантомные варианты построения дуг.

Как и раньше, нужно выбрать соответствующий вам вариант и зафиксировать его.

Стоит помнить о том, что не всегда является возможным построение дуги касательной с помощью указания радиуса. О том, что это невозможно, вам сообщит исчезновение всех фантомных вариантов после того, как вы введете желаемый радиус.

Пока что, это всё. Существуют и другие способы построения дуг, которые мы покроем в следующих уроках.

Видео:Аксонометрические Проекции Окружности #черчение #окружность #проекции #изометрияСкачать

Построение дуги окружности. Дуга по двум точкам, дуга по двум точкам и углу раствора.

Дуга по двум точкам.

Для того, чтобы построить дугу с указанием двух точек, вам нужно выбрать «Дуга по 2 точкам». В компактном меню либо же указать в меню сверху следующие команды «Инструменты» — «Геометрия» — «Дуги» — «Дуга по 2 точкам».

Для начала в нужном поле в свойственной панели от вас требуется ввести значение радиуса либо диаметра (к примеру, радиус в 100 мм) и нажать кнопку ввода.

С помощью курсора или же в свойственной панели указываете координаты начала и конца дуги. Экран отобразит фантомные варианты построения.

Вам нужно выбрать правильный и последовательно нажать пункты «Создать объект» и «Прервать команду».

Если вы хотите построить дугу по диаметрально противоположным точкам, то радиус и диаметр программа рассчитает самостоятельно.

Дуга по двум точкам и углу раствора.

Для того, чтобы построить дугу с указанием двух точек и угла раствора, нужно нажать «Дуга по 2 точкам и углу раствора». В компактном меню или же в меню сверху выбрать команды «Инструменты» — «Геометрия» — «Дуги» — «Дуга по 2 точкам и углу раствора».

В свойственной панели для начала нужно ввести значение угла (к примеру, 220 градусов) и нажать клавишу ввода.

Потом вам нужно указать положение начала и конца дуги. Координаты могут указываться с помощью курсора либо введя их в нужные поля свойственной панели.

Прочие параметры, такие, как центральная точка и диаметр, программа определит самостоятельно. Построение завершается кнопками «Создать объект» и «Прервать команду».

Нами были рассмотрены все возможности построения дуг в “Компас 3D”. Далее мы разберёмся, как строить эллипсы.

Видео:Окружность в прямоугольной изометрии КОМПАССкачать

Построение эллипса.

В программе “Компас 3D” у вас есть несколько возможностей построить эллипс:

произвольный эллипс
эллипс с указанием диагонали прямоугольника
центра и вершины прямоугольника
центра, середины стороны и вершины параллелограммы
эллипс с указанием трёх вершин параллелограмма
центра и трёх точек
с касанием двух кривых линий.

Первые три метода будут рассмотрены в данной статье.

Произвольный эллипс.

Для того, чтобы построить произвольный эллипс, вам нужно выбрать «Эллипс» в компактном меню либо найти следующие команды в верхней панели:«Инструменты» — «Геометрия» — «Эллипсы» — «Эллипс».

Для начала с помощью курсора вам нужно задать точку центра эллипса. Также её координаты можно ввести в свойственной панели.

Далее вам стоит указать конечные точки расположения двух полуосей с помощью курсора либо свойственной панели. При постройке эллипса с центральной точкой в пересечении координатной оси вы можете указать в свойственной панели длину полуосей

Для примера задаём длину первой оси как 100 мм, а второй – 50 мм и после каждого завершённого ввода жмём клавишу ввод.

Значение угла наклона первой оси к оси абсцисс программа способна рассчитать автоматически, но также мы имеем возможность введения его значения, при условии, что оно известно. Например, введём угол 45 градусов и нажмём клавишу ввода.

В результате эллипс поворачивается на необходимое значение угла. Для того, чтобы отрисовать оси, свойственная панель располагает соответствующей опцией. Для эллипса при постройке устанавливается любой стиль линии.

Эллипс по диагонали габаритного прямоугольника

Для того, чтобы построить эллипс по диагонали габаритного прямоугольника, нужно выбрать опцию в компактном меню «Эллипс по диагонали прямоугольника”. Или же выбрать в меню сверху соответствующие команды «Инструменты» — «Геометрия» — «Эллипсы» — «Эллипс по диагонали прямоугольника».

Как пример, для построения можно начертить произвольный прямоугольник. Если имеется значение угла наклона первой полуоси эллипса к оси абсцисс используемой координатной системы, его можно ввести в нужное поле свойственной панели (по умолчанию значение нулевой). Далее мы можем задать начало и конец диагоналей прямоугольника, который будет описываться вокруг эллипса.

Размеры полуосей рассчитываются программой.

Эллипс по центру и вершине габаритного прямоугольника.

Для того, чтобы построить такой эллипс нужно нажать кнопку в компактном меню «Эллипс по центру и вершине прямоугольника”. Или же в меню сверху выполнить следующие команды «Инструменты» — «Геометрия» — «Эллипсы» — «Эллипс по центру и вершине прямоугольника».

Как и раньше, мы можем начертить произвольный прямоугольник и провести его диагонали. Также у нас есть возможность задания угла, но в этом случае давайте разберём построение по умолчанию. Для начала нужно нажать кнопку «Эллипс по центру и вершине прямоугольника” и указать центр и вершину прямоугольника, в который будет вписан создаваемый эллипс.

Длины полуосей программа способна рассчитать самостоятельно. Для начала этого хватит, прочие методы построения эллипса мы можем рассмотреть в следующей статье. Продолжим рассматривать методы построения эллипса в программе “Компас 3D”.

Эллипс по центру, середине стороны и вершине описанного параллелограмма.

Для подобного построения нужно нажать «Эллипс по центру, середине стороны и вершине параллелограмма». В компактном меню, либо же в меню сверху определить команды «Инструменты» — «Геометрия» — «Эллипсы» — «Эллипс по центру, середине стороны и вершине параллелограмма».

Как пример, займёмся построением произвольного параллелограмма и его диагоналей. Нажав кнопку «Эллипс по центру, середине стороны и вершине параллелограмма», мы можем указать координаты центра, а также середины одной из сторон и вершины параллелограмма, в который будет вписан создаваемый эллипс.

Программа самостоятельно определит угол наклона первой полуоси к оси абсцисс в текущей координатной системе, а также определит длины полуосей.

Эллипс по трем вершинам параллелограмма.

Для выполнения построения нужно нажать кнопку «Эллипс по трем вершинам параллелограмма». В компактном меню, либо выбрать в панели сверху команды «Инструменты» — «Геометрия» — «Эллипсы» — «Эллипс по трем вершинам параллелограмма».

Далее с помощью курсора мы имеем возможность указать три вершины параллелограмма. Программа самостоятельно определит угол наклона первой полуоси к оси абсцисс в текущей системе координат, а также длины полуосей. Для того, чтобы отрисовать оси, нужно нажать соответствующую опцию в свойственной панели.

Эллипс по центру и трем точкам.

Для начала построения нужно нажать кнопку «Эллипс по центру и 3 точкам» в компактном меню, либо же указать следующие команды в панельном меню сверху: «Инструменты» — «Геометрия» — «Эллипсы» — «Эллипс по центру и 3 точкам».

Для начала с помощью курсора мы можем указать центральную точку эллипса, а также три принадлежащие ему точки. Координаты центральной точки и других точек задаются в свойственной панели. Построение можно завершить с помощью кнопки «Прервать команду».

Эллипс касательный к двум кривым.

Для того, чтобы построить такой эллипс, нужно нажать «Эллипс касательный к 2 кривым» в компактном меню, либо же выполнить команды в меню сверху «Инструменты» — «Геометрия» — «Эллипсы» — «Эллипс касательный к 2 кривым». Займёмся постройкой двух произвольных окружностей с разными диаметрами, находящихся на некотором расстоянии друг от друга.

Нажав опцию«Эллипс касательный к 2 кривым» мы можем указать точки на первом и втором объектах. Далее мы указываем третью точку прохождения эллипса и завершаем построение с помощью кнопки «Прервать команду».

Все способы, рассмотренные нами в панели свойств, могут также задавать стиль линий и оси для уже построенных эллипсов.

Видео:Окружность в прямоугольной изометрии 3 способ построенияСкачать

Урок №10. Строим окружность в программе Компас 3D.

Построить окружность в программе Компас довольно просто. Достаточно вызвать на компактной панели Окружность, либо зайти через основное меню, через пункты Инструменты-Геометрия-Окружности-Окружность.

Необходимо указать центр строящейся окружности, при помощи мыши Впрочем, можете ввести значения координат в меню снизу экрана.

Зафиксируем нашу окружность, для этого необходимо нажать на левую клавишу мыши, а затем Прервать команду.

Используя панель свойств, вы можете указать Диаметр или Радиус окружности. Соответственно, когда известен диаметр, вписываем значение в это поле, а когда радиус, в одноименное поле.

Окружность будет построена без осевых линий, однако их можно добавить простыми переключениями в настройках. Если необходимые осевые линии, достаточно нажать на кнопку Оси на панели внизу экрана. Все, линии появятся автоматически, без всяких дополнительных процедур.

Порой уже после построения и одобрения окружности, выясняется, что необходимо нанести оси. Для этого достаточно выделить окружность, активировать отрисовку осей на панели внизу и нажать на кнопку Создать объект.

Аналогичным образом можно изменить радиус или диаметр окружности, редактировать стили всех линий, включая осевые. Достаточно лишь войти в режим редактирования объекта.

В данном уроке, вы узнали, как строить различные окружности, задавать им параметры, быстро отрисовывать осевые линии.

Видео:КАК НАРИСОВАТЬ КРУГ В ИЗОМЕТРИИ (ОВАЛ В ИЗОМЕТРИЧЕСКОЙ ПРОЕКЦИИ).Скачать

Деление окружности на любое количество равных частей в КОМПАС — 3D с примером

Деление окружности на любое количество равных частей:

Чтобы выполнить шестое задание «Деление окружности на равные части» составим алгоритм последовательности выполнения работы:

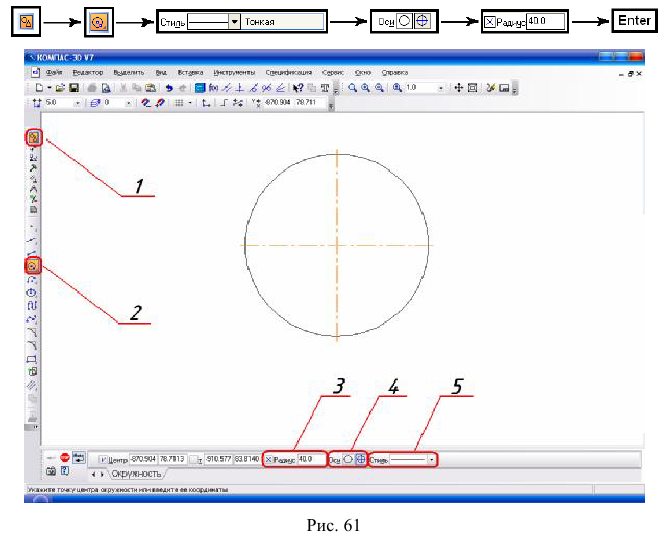
1) построить окружность (радиус 40 мм);
2) разделить окружность на равные части, допустим на 7;
3) построить вписанный в окружность семиугольник.

1. Построение окружности радиусом 40 мм. Войдите на страницу Геометрия (1)

Алгоритм построения выглядит следующим образом:

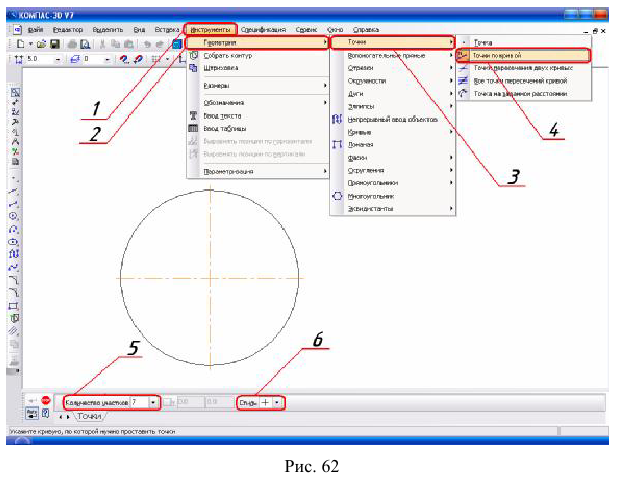
2. Деление окружности на 7 равных частей. Имея готовую окруж-

ность войдите в Строку меню (1) и щелчком левой кнопки мыши вызовите каскадное меню. Затем в Строке параметров (внизу рабочего поля) укажите Количество участков в данном случае 7 и выберите Стиль точки (рис. 62).

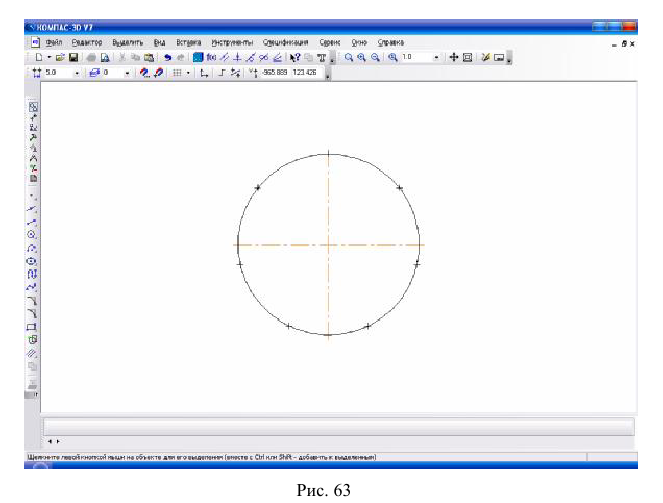
На рис. 63 показана окружность, поделённая на 7 равных частей.

Таким же образом можно построить деление окружности на любое количество равных частей.

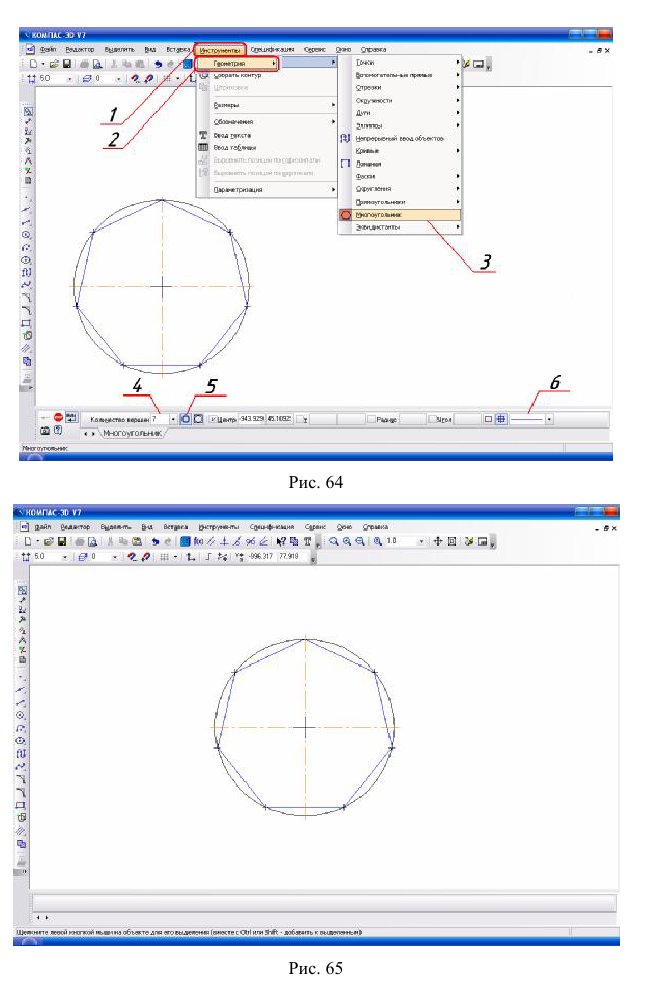
3. Построение семиугольника, вписанного в окружность. В заданную окружность можно вписать многоугольник.

Команда «Многоугольник» (3)из каскадного меню позволяет построить многоугольники с любым количеством вершин. Рассмотрим построение семиугольника.

Чтобы построить семиугольник необходимо следовать указаниям, приведённым ниже.

Войдите в Строку меню (1)и щелчком левой кнопки мы-
ши вызовите каскадное меню. После выбора команды «Многоуголь-
ник» (5)из каскадного меню на экране автоматически появляется
Строка параметров, в которой укажите Количество вершин

в данном случае 7, выберите многоугольник «По описанной окружности »и укажите «Стиль линии»(рис 64)
Алгоритмы для построения семиугольника:

На рис. 65 — семиугольник, вписанный в окружность.

Рекомендую подробно изучить предметы:

Инженерная графика
Начертательная геометрия
Компас
Автокад
Черчение
Проекционное черчение
Аксонометрическое черчение
Строительное черчение
Техническое черчение
Геометрическое черчение

Ещё лекции с примерами решения и объяснением:

Алгоритм построения контура технической детали с сопряжениями в КОМПАС — 3D
Алгоритм построения двутавра в КОМПАС — 3D
Создание модели зубчатой шестерни раздаточного редуктора рабочего рольганга в КОМПАС — 3D
Создание моделей деталей раздаточного редуктора с использованием вариационной параметризации в КОМПАС — 3D
Деление отрезка прямой на любое число равных частей в КОМПАС — 3D
Деление угла на две равные части в КОМПАС — 3D
Деление прямого угла на три равные части в КОМПАС — 3D
Построение угла, равного заданному в КОМПАС — 3D

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.