В данной публикации мы рассмотрим формулы, с помощью которых можно найти высоту трапеции, а также разберем примеры решения задач для закрепления материала.
Напомним, высотой трапеции называется отрезок, соединяющий оба ее основания и перпендикулярный им.
- Нахождение высоты трапеции
- Через длины сторон
- Через боковую сторону и прилежащий угол
- Через диагонали и угол между ними
- Через площадь
- Примеры задач
- Высота трапеции как найти в окружность
- Описанная окружность и трапеция
- Трапеция. Формулы, признаки и свойства трапеции
- Основные свойства трапеции
- Сторона трапеции
- Формулы определения длин сторон трапеции:
- Средняя линия трапеции
- Формулы определения длины средней линии трапеции:
- Высота трапеции
- Формулы определения длины высоты трапеции:
- Диагонали трапеции
- Формулы определения длины диагоналей трапеции:
- Площадь трапеции
- Формулы определения площади трапеции:
- Периметр трапеции
- Формула определения периметра трапеции:
- Окружность описанная вокруг трапеции
- Формула определения радиуса описанной вокруг трапеции окружности:
- Окружность вписанная в трапецию
- Формула определения радиуса вписанной в трапецию окружности
- Другие отрезки разносторонней трапеции
- Формулы определения длин отрезков проходящих через трапецию:
- Нахождение высоты трапеции: формулы и примеры задач
- Нахождение высоты трапеции
- Через длины сторон
- Через боковую сторону и прилежащий угол
- Через диагонали и угол между ними
- Через площадь
- Примеры задач
- Описанная окружность и трапеция
- 🎥 Видео
Видео:Основания равнобедренной трапеции равны 72 и 30. Центр окружности, описанной около трапеции... (ЕГЭ)Скачать

Нахождение высоты трапеции
Через длины сторон
Если известны длины всех четырех сторон трапеции, ее высота рассчитывается по формуле ниже:
Через боковую сторону и прилежащий угол
Высоту трапеции можно вычислить, если знать длину любой из ее боковых сторон и значение прилежащего к ней и основанию угла.
Через диагонали и угол между ними
Зная длину оснований трапеции, а также диагоналей и угол между ними, вычислить высоту удастся по формуле:
Если сумму оснований заменить длиной средней линии (m), то формула будет выглядеть следующим образом:
Средняя линия трапеции (m) равняется полусумме ее оснований, т.е m = (a+b) /2.
Через площадь
Высоту трапеции можно вычислить, если известны ее площадь и длины оснований (или средней линии).
Примечание: формулы для нахождения высоты равнобедренной и прямоугольной трапеций представлены на нашем сайте в отдельных публикациях.
Видео:Задача про трапецию, описанную около окружностиСкачать

Примеры задач
Задание 1
Найдите высоту трапеции, если ее основания равны 9 и 6 см, а боковые стороны – 4 и 5 см.
Решение
Т.к. у нас есть длины всех сторон, мы можем воспользоваться первой формулой для вычисления требуемого значения:
Кстати, т.к. высота равна одной из боковой сторон трапеции, значит она является прямоугольной.
Задание 2
Площадь трапеции равна 26 см 2 . Найдите ее высоту, если основания равны 10 и 3 см.
Решение
В данном случае можно применить последнюю из рассмотренных формул:
Видео:Геометрия Задача № 26 Найти радиус вписанной в трапецию окружностиСкачать

Высота трапеции как найти в окружность
Видео:Трапеция. Практическая часть - решение задачи. 8 класс.Скачать

Описанная окружность и трапеция
Описанная окружность и трапеция. Здравствуйте! Для вас ещё одна публикация, в которой рассмотрим задачи с трапециями. Задания входят в состав экзамена по математике. Здесь они объединены в группу, дана не просто одна трапеция, а комбинация тел – трапеция и окружность. Большинство из таких задачек решаются устно. Но есть и такие на которые нужно обратить особое внимание, например, задача 27926.
Какую теорию необходимо помнить? Это:
2. Теорему Пифагора. *Куда мы без неё )
Задачи с трапециями, которые имеются на блоге можно посмотреть здесь .
27924. Около трапеции описана окружность. Периметр трапеции равен 22, средняя линия равна 5. Найдите боковую сторону трапеции.
Отметим, что описать окружность можно только около равнобедренной трапеции. Нам дана средняя линия, значит можем определить сумму оснований, то есть:
Значит сумма боковых сторон будет равна 22–10=12 (периметр минус основания). Так как боковые стороны равнобедренной трапеции равны, то одна сторона будет равна шести.
27925. Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 60 0 , большее основание равно 12. Найдите радиус описанной окружности этой трапеции.
Если вы решали задачи с окружностью и вписанным в неё шестиугольником, то сразу озвучите ответ – радиус равен 6. Почему?
Посмотрите: равнобедренная трапеция с углом при основании равным 60 0 и равными сторонами AD, DC и CB, представляет собой половину правильного шестиугольника:
В таком шестиугольнике отрезок соединяющий противоположные вершины проходит через центр окружности. *Центр шестиугольника и центр окружности совпадают, подробнее здесь п.6
То есть большее основание этой трапеции совпадает с диаметром описанной окружности. Таким образом радиус равен шести.
*Конечно, можно рассмотреть равенство треугольников ADO, DOС и OCB. Доказать что они равносторонние. Далее сделать вывод о том, что угол AOB равен 180 0 и точка О равноудалена от вершин A, D, C и B, а и значит АО=ОВ=12/2=6.
27926. Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5. Найдите высоту трапеции.
Отметим, что центр описанной окружности лежит на оси симметрии, при чём если построить высоту трапеции проходящую через этот центр, то она при пересечении с основаниями разделит их пополам. Покажем это на эскизе, также соединим центр с вершинами:
Отрезок EF является высотой трапеции, его нам нужно найти.
В прямоугольном треугольнике OFC нам известна гипотенуза (это радиус окружности), FC=3 (так как DF=FC). По теореме Пифагора можем вычислить OF:
В прямоугольном треугольнике OEB нам известна гипотенуза (это радиус окружности), EB=4 (так как AE=EB). По теореме Пифагора можем вычислить OE:
Таким образом EF=FO+OE=4+3=7.
Теперь важный нюанс!
В этой задаче на рисунке чётко показано, что основания лежат по разные стороны от центра окружности, поэтому задача решается именно так.
А если бы в условии не было дано эскиза?
Тогда у задачи было бы два ответа. Почему? Посмотрите внимательно – в любую окружность можно вписать две трапеции с заданными основаниями:
*То есть при данных основаниях трапеции и радиусе окружности существует две трапеции.
И решение будет «второго варианта» будет следующим.
По теореме Пифагора вычисляем OF:
Также вычислим OE:
Таким образом EF=FO–OE=4–3=1.
Конечно, в задаче с кратким ответом на ЕГЭ двух ответов быть не может, и подобная задача без эскиза дана не будет. Поэтому обратите особое внимание на эскиз! А именно: как расположены основания трапеции. А вот в заданиях с развёрнутым ответом такая в прошлые годы присутствовала (немного с усложнённым условием). Тот, кто рассматривал только один вариант расположения трапеции теряли балл на этом задании.
27937. Около окружности описана трапеция, периметр которой равен 40. Найдите ее среднюю линию.
Здесь сразу следует вспомнить свойство четырёхугольника описанного около окружности:
Суммы противоположных сторон любого четырёхугольника описанного около окружности равны.
А средняя линия равна половине суммы оснований, то есть 10.
27938. Периметр прямоугольной трапеции, описанной около окружности, равен 22, ее большая боковая сторона равна 7. Найдите радиус окружности.
Радиус окружности равен половине высоты. Используя свойство указанное в предыдущей задаче получим:
Большая сторона у нас это СВ, следовательно можем вычислить AD=11–CB=11–7=4. Таким образом, радиус будет равен 2.
27915. Найдите высоту трапеции, в которую вписана окружность радиуса 1.
27936. Боковые стороны трапеции, описанной около окружности, равны 3 и 5. Найдите среднюю линию трапеции.
Видео:Радиус описанной окружности трапецииСкачать

Трапеция. Формулы, признаки и свойства трапеции
Параллельные стороны называются основами трапеции, а две другие боковыми сторонами
Так же, трапецией называется четырехугольник, у которого одна пара противоположных сторон параллельна, и стороны не равны между собой.
- Основы трапеции — параллельные стороны
- Боковые стороны — две другие стороны
- Средняя линия — отрезок, соединяющий середины боковых сторон.
- Равнобедренная трапеция — трапеция, у которой боковые стороны равны
- Прямоугольная трапеция — трапеция, у которой одна из боковых сторон перпендикулярна основам
 |  |
| Рис.1 | Рис.2 |
Видео:Задача 6 №27926 ЕГЭ по математике. Урок 141Скачать

Основные свойства трапеции
AK = KB, AM = MC, BN = ND, CL = LD
3. Средняя линия трапеции параллельна основаниям и равна их полусумме:
| m = | a + b |
| 2 |
BC : AD = OC : AO = OB : DO
d 1 2 + d 2 2 = 2 a b + c 2 + d 2
Видео:ТРАПЕЦИЯ — Что такое трапеция, Виды Трапеций, Площадь Трапеции // Геометрия 8 классСкачать

Сторона трапеции
Формулы определения длин сторон трапеции:
a = b + h · ( ctg α + ctg β )
b = a — h · ( ctg α + ctg β )
a = b + c· cos α + d· cos β
b = a — c· cos α — d· cos β
4. Формулы боковых сторон через высоту и углы при нижнем основании:
| с = | h | d = | h |
| sin α | sin β |
Видео:Около трапеции описана окружностьСкачать
Средняя линия трапеции
Формулы определения длины средней линии трапеции:
1. Формула определения длины средней линии через длины оснований:
| m = | a + b |
| 2 |
2. Формула определения длины средней линии через площадь и высоту:
| m = | S |
| h |
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Высота трапеции
Формулы определения длины высоты трапеции:
h = c· sin α = d· sin β
2. Формула высоты через диагонали и углы между ними:
| h = | sin γ · | d 1 d 2 | = | sin δ · | d 1 d 2 |
| a + b | a + b |
3. Формула высоты через диагонали, углы между ними и среднюю линию:
| h = | sin γ · | d 1 d 2 | = | sin δ · | d 1 d 2 |
| 2 m | 2 m |
4. Формула высоты трапеции через площадь и длины оснований:
| h = | 2S |
| a + b |
5. Формула высоты трапеции через площадь и длину средней линии:
| h = | S |
| m |
Видео:ВЫСОТЫ ТРАПЕЦИИ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Диагонали трапеции
Формулы определения длины диагоналей трапеции:
d 1 = √ a 2 + d 2 — 2 ad· cos β
d 2 = √ a 2 + c 2 — 2 ac· cos β
2. Формулы диагоналей через четыре стороны:
| d 1 = | √ | d 2 + ab — | a ( d 2 — c 2 ) |
| a — b |
| d 2 = | √ | c 2 + ab — | a ( c 2 — d 2 ) | a — b |
d 1 = √ h 2 + ( a — h · ctg β ) 2 = √ h 2 + ( b + h · ctg α ) 2
d 2 = √ h 2 + ( a — h · ctg α ) 2 = √ h 2 + ( b + h · ctg β ) 2
d 1 = √ c 2 + d 2 + 2 ab — d 2 2
d 2 = √ c 2 + d 2 + 2 ab — d 1 2
Видео:Боковые стороны трапеции, описанной около окружности, равны 13 и 1. Найдите среднюю линию трапеции.Скачать
Площадь трапеции
Формулы определения площади трапеции:
1. Формула площади через основания и высоту:
| S = | ( a + b ) | · h |
| 2 |
3. Формула площади через диагонали и угол между ними:
| S = | d 1 d 2 | · sin γ | = | d 1 d 2 | · sin δ |
| 2 | 2 |
4. Формула площади через четыре стороны:
| S = | a + b | √ | c 2 — | ( | ( a — b ) 2 + c 2 — d 2 | ) | 2 |
| 2 | 2( a — b ) |
5. Формула Герона для трапеции
| S = | a + b | √ ( p — a )( p — b )( p — a — c )( p — a — d ) |
| | a — b | |
| p = | a + b + c + d | — полупериметр трапеции. |
| 2 |
Видео:Окружность и трапеция | ЕГЭ-2018. Задание 16. Математика. Профильный уровень | Борис Трушин +Скачать

Периметр трапеции
Формула определения периметра трапеции:
1. Формула периметра через основания:
Видео:Как найти стороны равнобокой трапеции, описанной около трёх попарно касающихся равных окружностей?Скачать
Окружность описанная вокруг трапеции
Формула определения радиуса описанной вокруг трапеции окружности:
1. Формула радиуса через стороны и диагональ:
| R = | a·c·d 1 |
| 4√ p ( p — a )( p — c )( p — d 1) |
| p = | a + c + d 1 |
| 2 |
a — большее основание
Видео:Задание 16 ОГЭ по математике. Окружность вписана в трапецию.Скачать

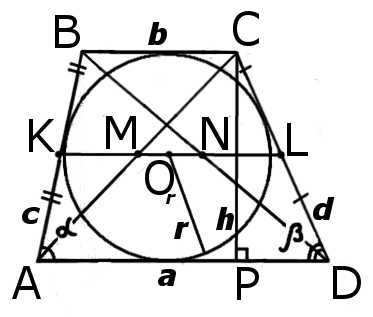
Окружность вписанная в трапецию
Формула определения радиуса вписанной в трапецию окружности
1. Формула радиуса вписанной окружности через высоту:
| r = | h |
| 2 |
Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

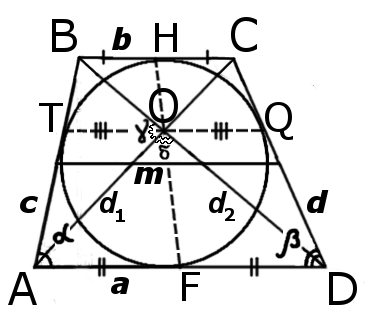
Другие отрезки разносторонней трапеции
Формулы определения длин отрезков проходящих через трапецию:
1. Формула определения длин отрезков проходящих через трапецию:
| KM = NL = | b | KN = ML = | a | TO = OQ = | a · b |
| 2 | 2 | a + b |
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Видео:Где центр окружности? ТрапецияСкачать

Нахождение высоты трапеции: формулы и примеры задач
В данной публикации мы рассмотрим формулы, с помощью которых можно найти высоту трапеции, а также разберем примеры решения задач для закрепления материала.
Напомним, высотой трапеции называется отрезок, соединяющий оба ее основания и перпендикулярный им.
Видео:Трапеция и вписанная окружностьСкачать

Нахождение высоты трапеции
Через длины сторон
Если известны длины всех четырех сторон трапеции, ее высота рассчитывается по формуле ниже:
Через боковую сторону и прилежащий угол
Высоту трапеции можно вычислить, если знать длину любой из ее боковых сторон и значение прилежащего к ней и основанию угла.
Через диагонали и угол между ними
Зная длину оснований трапеции, а также диагоналей и угол между ними, вычислить высоту удастся по формуле:
Если сумму оснований заменить длиной средней линии (m), то формула будет выглядеть следующим образом:
Средняя линия трапеции (m) равняется полусумме ее оснований, т.е m = (a+b) /2.
Через площадь
Высоту трапеции можно вычислить, если известны ее площадь и длины оснований (или средней линии).
Примечание: формулы для нахождения высоты равнобедренной и прямоугольной трапеций представлены на нашем сайте в отдельных публикациях.
Видео:Задача.Высота трапеции, образованной касательными к двум окружностям.Скачать

Примеры задач
Задание 1
Найдите высоту трапеции, если ее основания равны 9 и 6 см, а боковые стороны – 4 и 5 см.
Решение
Т.к. у нас есть длины всех сторон, мы можем воспользоваться первой формулой для вычисления требуемого значения:
Кстати, т.к. высота равна одной из боковой сторон трапеции, значит она является прямоугольной.
Задание 2
Площадь трапеции равна 26 см 2 . Найдите ее высоту, если основания равны 10 и 3 см.
Решение
В данном случае можно применить последнюю из рассмотренных формул:
Видео:Как найти высоту трапеции, зная все стороны?Скачать
Описанная окружность и трапеция
Описанная окружность и трапеция. Здравствуйте! Для вас ещё одна публикация, в которой рассмотрим задачи с трапециями. Задания входят в состав экзамена по математике. Здесь они объединены в группу, дана не просто одна трапеция, а комбинация тел – трапеция и окружность. Большинство из таких задачек решаются устно. Но есть и такие на которые нужно обратить особое внимание, например, задача 27926.
Какую теорию необходимо помнить? Это:
2. Теорему Пифагора. *Куда мы без неё )
Задачи с трапециями, которые имеются на блоге можно посмотреть здесь .
27924. Около трапеции описана окружность. Периметр трапеции равен 22, средняя линия равна 5. Найдите боковую сторону трапеции.
Отметим, что описать окружность можно только около равнобедренной трапеции. Нам дана средняя линия, значит можем определить сумму оснований, то есть:
Значит сумма боковых сторон будет равна 22–10=12 (периметр минус основания). Так как боковые стороны равнобедренной трапеции равны, то одна сторона будет равна шести.
27925. Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 60 0 , большее основание равно 12. Найдите радиус описанной окружности этой трапеции.
Если вы решали задачи с окружностью и вписанным в неё шестиугольником, то сразу озвучите ответ – радиус равен 6. Почему?
Посмотрите: равнобедренная трапеция с углом при основании равным 60 0 и равными сторонами AD, DC и CB, представляет собой половину правильного шестиугольника:
В таком шестиугольнике отрезок соединяющий противоположные вершины проходит через центр окружности. *Центр шестиугольника и центр окружности совпадают, подробнее здесь п.6
То есть большее основание этой трапеции совпадает с диаметром описанной окружности. Таким образом радиус равен шести.
*Конечно, можно рассмотреть равенство треугольников ADO, DOС и OCB. Доказать что они равносторонние. Далее сделать вывод о том, что угол AOB равен 180 0 и точка О равноудалена от вершин A, D, C и B, а и значит АО=ОВ=12/2=6.
27926. Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5. Найдите высоту трапеции.
Отметим, что центр описанной окружности лежит на оси симметрии, при чём если построить высоту трапеции проходящую через этот центр, то она при пересечении с основаниями разделит их пополам. Покажем это на эскизе, также соединим центр с вершинами:
Отрезок EF является высотой трапеции, его нам нужно найти.
В прямоугольном треугольнике OFC нам известна гипотенуза (это радиус окружности), FC=3 (так как DF=FC). По теореме Пифагора можем вычислить OF:
В прямоугольном треугольнике OEB нам известна гипотенуза (это радиус окружности), EB=4 (так как AE=EB). По теореме Пифагора можем вычислить OE:
Таким образом EF=FO+OE=4+3=7.
Теперь важный нюанс!
В этой задаче на рисунке чётко показано, что основания лежат по разные стороны от центра окружности, поэтому задача решается именно так.
А если бы в условии не было дано эскиза?
Тогда у задачи было бы два ответа. Почему? Посмотрите внимательно – в любую окружность можно вписать две трапеции с заданными основаниями:
*То есть при данных основаниях трапеции и радиусе окружности существует две трапеции.
И решение будет «второго варианта» будет следующим.
По теореме Пифагора вычисляем OF:
Также вычислим OE:
Таким образом EF=FO–OE=4–3=1.
Конечно, в задаче с кратким ответом на ЕГЭ двух ответов быть не может, и подобная задача без эскиза дана не будет. Поэтому обратите особое внимание на эскиз! А именно: как расположены основания трапеции. А вот в заданиях с развёрнутым ответом такая в прошлые годы присутствовала (немного с усложнённым условием). Тот, кто рассматривал только один вариант расположения трапеции теряли балл на этом задании.
27937. Около окружности описана трапеция, периметр которой равен 40. Найдите ее среднюю линию.
Здесь сразу следует вспомнить свойство четырёхугольника описанного около окружности:
Суммы противоположных сторон любого четырёхугольника описанного около окружности равны.
А средняя линия равна половине суммы оснований, то есть 10.
27938. Периметр прямоугольной трапеции, описанной около окружности, равен 22, ее большая боковая сторона равна 7. Найдите радиус окружности.
Радиус окружности равен половине высоты. Используя свойство указанное в предыдущей задаче получим:
Большая сторона у нас это СВ, следовательно можем вычислить AD=11–CB=11–7=4. Таким образом, радиус будет равен 2.
27915. Найдите высоту трапеции, в которую вписана окружность радиуса 1.
27936. Боковые стороны трапеции, описанной около окружности, равны 3 и 5. Найдите среднюю линию трапеции.
🎥 Видео
Окружность вписанная в треугольник и описанная около треугольника.Скачать






























