Вершина а треугольника авс

Геометрия | 10 — 11 классы

Вершина А треугольника АВС лежит в плоскости а, вершины В и С расположены по одну сторону от этой плоскости.

Отрезок АD — медиана треугольника АВС.

Через точки B, D, C проведены параллельные прямые, пересекающие плоскость в точках В1, D1, C1 соответственно.

Найдите длину DD1, если ВВ1 = 2 см и СС1 = 12 см.

Через прямую ВВ₁ и ВС можно провести единственную плоскость.

Так как точка D лежит на ВС, она лежит в этой плоскости.

DD₁║BB₁ и CC₁║BB₁ значит DD₁ и СС₁ так же лежат в этой плоскости.

Эта плоскость пересекает плоскость α по прямой В₁С₁, значит и точка D₁ лежит на линии пересечения плоскостей.

Итак, В₁ВСС₁ — плоский четырехугольник, у которого две стороны параллельны, т.

DD₁ параллелен основаниям трапеции и проходит через середину боковой стороны, значит является средней линией.

DD₁ = (СС₁ + ВВ₁) / 2 = (12 + 2) / 2 = 7 см.

Видео:Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать

105 баллов?

Вне плоскости альфа расположен треугольник ABC у которого медианы АА1 и BB1 параллельны плоскости альфа Через вершины В и С треугольника проведены параллельные прямые, которые пересекают плоскость альфа соот — ветственно в точках Е и F.

Докажите, что ECBF — параллелограмм.

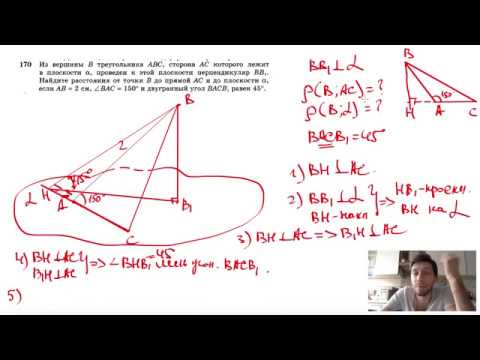
Видео:№170. Из вершины В треугольника ABC, сторона АС которого лежит в плоскости а, проведен к этойСкачать

Какое из утверждений верно?

Какое из утверждений верно?

А) если две точки треугольника лежат в плоскости, то и весь треугольник лежит в плоскости ;

б) прямая, лежащая в плоскости треугольника пересекает его стороны ;

в) любые две плоскости имеют только одну общую точку ;

г) через две точки проходит плоскость, и притом только одна ;

д) прямая лежит в плоскости треугольника , если она пересекает две прямые, содержащие стороны треугольника.

Видео:№145. Через вершину А прямоугольного треугольника ABC с прямым углом С проведена прямая AD,Скачать

Плоскость пересекает стороны АВ и ВС треугольника АВС в точках М и К соответственно и параллельна стороне АС, МК = 4см, МВ : МА = 2 : 3?

Плоскость пересекает стороны АВ и ВС треугольника АВС в точках М и К соответственно и параллельна стороне АС, МК = 4см, МВ : МА = 2 : 3.

Найдите длину стороны АС треугольника Точка В не лежит в плоскости треугольника АДС.

Точки М Р К и Е — середины отрезков АВ ВС СД и АД соответственно, МК = РЕ = 10см, АС = 12см.

Найдите длину отрезка ВД.

Через параллельные прямые а и в проведены две плоскости, которые пересекаются по прямой с.

Докажите, что прямые а и в параллельны прямой с.

Видео:№973. Даны координаты вершин треугольника ABC: А (4; 6), В (-4; 0), С (-1; -4). Напишите уравнениеСкачать

Из точки О — точки пересечения медиан равностороннего треугольника АВС — проведен перпендикуляр ОМ до плоскости треугольника, найти угол наклона прямой МА к плоскости АВС, если ОМ = АВ = 6?

Из точки О — точки пересечения медиан равностороннего треугольника АВС — проведен перпендикуляр ОМ до плоскости треугольника, найти угол наклона прямой МА к плоскости АВС, если ОМ = АВ = 6.

Видео:№942. Найдите медиану AM треугольника ABC, вершины которого имеют координаты: А(0; 1), В(1; -4)Скачать

10 КЛАСС?

ПОМОГИТЕ ПОЖАЛУЙСТА СРОЧНО НАДО!

Вне плоскости альфа расположен треугольник ABC, у которого медианы АА1 и BB1 параллельны плоскости альфа.

Через вершины В и С треугольника проведены параллельные прямые, которые пересекают плоскость альфа соответственно в точках E и F.

Докажите, что ECBF — параллелограмм.

Видео:Через середину К медианы ВМ треугольника АВС и вершину А проведена прямая пересекающая сторону ВС вСкачать

Плоскость альфа параллельна плоскости равностороннего треугольника ABC?

Плоскость альфа параллельна плоскости равностороннего треугольника ABC.

Через его вершины проведены параллельные прямые, пересекающие плоскость альфа в точках A1 B1 C1.

Вычислите площадь треугольника A1B1C1( в см2), если AB = 6см.

Видео:№1049. Найдите углы треугольника с вершинами А (-1; √3), В(1;-√3 )Скачать

Вне плоскости альфа расположен треугольник ABC у которого медианы АА1 и BB1 параллельны плоскости альфа Через вершины В и С треугольника проведены параллельные прямые, которые пересекают плоскость аль?

Вне плоскости альфа расположен треугольник ABC у которого медианы АА1 и BB1 параллельны плоскости альфа Через вершины В и С треугольника проведены параллельные прямые, которые пересекают плоскость альфа соот — ветственно в точках Е и F.

Докажите, что ECBF — параллелограмм.

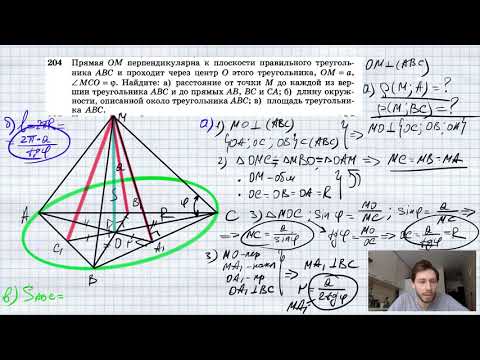
Видео:№204. Прямая ОМ перпендикулярна к плоскости правильного треугольника ABC и проходит через центр ОСкачать

Точка К, удаленная от плоскости треугольника АВС на 4см находится на равном расстоянии от его вершин?

Точка К, удаленная от плоскости треугольника АВС на 4см находится на равном расстоянии от его вершин.

Стороны треугольника равны 12см.

Вычислите : а)Длину проекции отрезка КВ на плоскость треугольника ; б)Расстояние от точки К до вершин треугольника.

Видео:Определение натуральной величины треугольника АВС методом вращения вокруг горизонтали или фронталиСкачать

1) длина сторон прямоугольника равна 6 и 8?

1) длина сторон прямоугольника равна 6 и 8.

Через точку О пересечения диагоналей прямоугольника проведена прямая ОК, перпендикулярная его плоскости.

Найдите расстояние от точки К до вершин прямоугольника, если ОК = 12.

2) длина сторон треугольника АВС соответственно равны : ВС = 15, АВ = 13, АС = 4.

Плоскость а, проходящая через сторону АС, образует с плоскостью треугольника угол в 30 градусов.

Найдите расстояние от вершины В до плоскости а.

Видео:Определение натуральной величины треугольника АВС методом замены плоскостей проекцииСкачать

Треугольник АВС расположен вне плоскости а?

Треугольник АВС расположен вне плоскости а.

Его вершины удалены от плоскости а на расстояния равные, 23 см , 15 см и 28 см.

Найдите расстояние от точки пересечения медиан треугольника до этой плоскости.

Вы открыли страницу вопроса Вершина А треугольника АВС лежит в плоскости а, вершины В и С расположены по одну сторону от этой плоскости?. Он относится к категории Геометрия. Уровень сложности вопроса – для учащихся 10 — 11 классов. Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие ответы по интересующей теме. Чтобы получить наиболее развернутый ответ, можно просмотреть другие, похожие вопросы в категории Геометрия, воспользовавшись поисковой системой, или ознакомиться с ответами других пользователей. Для расширения границ поиска создайте новый вопрос, используя ключевые слова. Введите его в строку, нажав кнопку вверху.

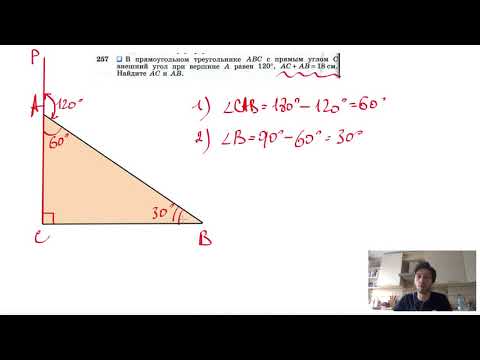
Видео:№257. В прямоугольном треугольнике ABC с прямым углом С внешний угол при вершине А равен 120°Скачать

Треугольник

Треугольник — это замкнутая ломаная линия, состоящая из трёх звеньев:

Вершины ломаной называются вершинами треугольника, а её звенья — сторонами треугольника. Углы, образованные двумя сторона треугольника, называются углами треугольника:

В треугольнике ABC вершины A, B и C — это вершины треугольника, звенья AB, BC и CA — стороны треугольника. Три угла — ∠ABC, ∠BCA и ∠CAB — углы треугольника. Часто углы треугольника обозначаются только одной буквой: ∠A, ∠B, ∠C.

Треугольник обычно обозначается тремя буквами, стоящими при его вершинах. Например, треугольник ABC, или BCA, или CBA. Вместо слова треугольник часто используется знак . Так, запись ABC будет читаться: треугольник ABC .

У каждого треугольника 3 вершины, 3 стороны и 3 угла.

Видео:№155. Через вершину прямого угла С равнобедренного прямоугольного треугольника ABCСкачать

Высота

Высота треугольника — это перпендикуляр, опущенный из вершины треугольника на его основание. Высота треугольника может быть опущена и на продолжение основания.

Отрезок BN — это высота ABC. Отрезок EL высота DEF, опущенная на продолжение стороны DF.

Длина высоты — это длина отрезка от вершины угла до пересечения с основанием.

Каждый треугольник имеет три высоты.

Видео:№1048. Найдите косинусы углов треугольника с вершинами А (2; 8),Скачать

Биссектриса

Биссектриса угла треугольника — прямая, делящая угол треугольника пополам. Длина отрезка этой прямой от вершины угла до точки пересечения с противоположной стороной называется длиной биссектрисы.

Отрезок BN — это биссектриса ABC.

Каждый треугольник имеет три биссектрисы.

Видео:№475. Начертите треугольник ABC. Через вершину А проведите две прямые так, чтобы они разделилиСкачать

Медиана

Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Длина этого отрезка называется длиной медианы.

Отрезок BN — это медиана ABC.

Видео:Вычисляем угол через координаты вершинСкачать

Треугольник. Медиана, биссектриса, высота, средняя линия.

теория по математике 📈 планиметрия

Треугольник – это геометрическая фигура, состоящая из трех точек на плоскости, которые не лежат на одной прямой, и трех последовательно соединяющих их отрезков.

Точки называют вершинами треугольника, а отрезки – сторонами. Вершины треугольника обозначают заглавными латинскими буквами.

Виды треугольников по углам

Треугольники классифицируются по углам: остроугольные; тупоугольные; прямоугольные.

Остроугольные	Тупоугольные	Прямоугольные
Остроугольным треугольником называется треугольник, у которого все три угла острые. На рисунке показан такой остроугольный треугольник АВС.	Тупоугольным называется треугольник, у которого есть тупой угол. В треугольнике может быть только один тупой угол. На рисунке показан треугольник такого вида, где угол М – тупой.	Прямоугольным называется треугольник, у которого есть угол, равный 90 0 (прямой угол). На рисунке угол С равен 90 0 . Такой угол в любом прямоугольном треугольнике – единственный.

Виды треугольников по сторонам

Треугольники классифицируются по сторонам: разносторонний; равнобедренный; равносторонний.

Разносторонний	Равнобедренный	Равносторонний
Треугольник называется разносторонним, если у него длины всех сторон разные. На рисунке показан такого вида треугольник АВС.	Треугольник называется равнобедренным, если у него две стороны равны. На рисунке показан равнобедренный треугольник АВС, у которого АВ=ВС.	Треугольник называется равносторонним, если у него все стороны равны. На рисунке показан такой треугольник, у него АВ=ВС=АС.

Видео:Геометрия Окружность проходит через вершины А и С треугольника АВС и пересекает его стороны АВ и ВССкачать

Медиана, биссектриса, высота, средняя линия треугольника

Медиана

Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.

В любом треугольнике можно провести три медианы, так как сторон – три. На рисунке показаны медианы треугольника АВС: AF, EC, BD.

По данному рисунку также видно, что медианы треугольника пересекаются в одной точке – точке О. Это справедливо для любого треугольника.

Биссектриса

Биссектрисой треугольника называется луч, исходящий из вершины угла треугольника и делящий его пополам.

В любом треугольнике можно провести три биссектрисы, так как углов – три. На рисунке показаны биссектрисы треугольника ЕDC: DD₁, EE₁ и CC₁.

По рисунку также видно, что биссектрисы имеют одну точку пересечения. Это справедливо для любого треугольника.

Высота

Высота треугольника – это перпендикуляр, проведенный из вершины треугольника к противоположной стороне.

На рисунке показаны высоты треугольника АВС: АН₁, ВН₂ и СН₃.

По рисунку видно, что высоты треугольника пересекаются в одной точке. Это также справедливо для любого треугольника.

Средняя линия

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон. На рисунке показаны три средние линии треугольника АВС: MN, KN и MK.

Средняя линия обладает следующими свойствами: она параллельна противоположной стороне; она равна половине противоположной стороны. Так, на данном рисунке MN параллельна АС, KN параллельна АВ, MK параллельна ВС. Также MN=0,5АС, KN=0,5АВ и MK=0,5ВС. Например, если известно, что сторона АС=20 см, то средняя линия МN равна половине АС, то есть МN=10 см. Или, например, если средняя линия МК=12 см, то сторона ВС будет в два раза больше, то есть ВС=24 см.

Выполним чертеж окружности, описанной около треугольника АВС, покажем на нём все дополнительные элементы.

При построении прямой АО образовалась точка пересечения этой прямой с окружностью, обозначим её буквой Е и соединим с точкой В и с точкой С. Получим вписанные углы АВЕ и АСЕ, опирающиеся на диаметр АЕ, следовательно угол АВЕ и АСЕ равны по 90 0 .

Рассмотрим треугольники АВЕ и АВF: у них углы АВЕ и АFВ прямые, угол ЕАВ – общий, следовательно, эти треугольники подобны.

Составим отношение сторон:

A E A B . . = A B A F . . откуда по свойству пропорции АВ 2 =АЕ ∙ АF

Рассмотрим треугольники АСЕ и ADF, у которых углы АСЕ и AFD прямые, а угол FAD – общий. Значит, треугольники АСЕ и ADF подобны.

Составим отношение сторон:

A E A D . . = A C A F . . ; откуда выразим AD= A E ∙ A F А C . . = A E ∙ A F A C . .

Теперь рассмотрим наши два полученных равенства: АВ 2 =АЕ ∙ АF и AD= A E ∙ A F A C . .

Видим, что 36 2 =АЕ ∙ АF (подставили вместо АВ значение 36), также у нас известно, что АС=54. Найдем из второго равенства AD= A E ∙ A F A C . . = 36 2 54 . . = 24

Теперь найдем CD=AC-AD=54-24=30

pазбирался: Даниил Романович | обсудить разбор | оценить

На клетчатой бумаге с размером клетки 1х1 изображен треугольник АВС. Найти длину его средней линии, параллельной стороне АС.

Для решения задачи надо вспомнить свойство средней линии: она параллельна основанию и равна его половине. Следовательно, чтобы найти длину средней линии, надо сторону треугольника разделить пополам. Найдем сторону треугольника, которой параллельна средняя линия, т.е. АС, сосчитав клетки, получим, что АС равна 8. Значит, средняя линия равна 8:2=4.

pазбирался: Даниил Романович | обсудить разбор | оценить

В треугольнике АВС известно, что угол ВАС равен 84 0 , АD – биссектриса. Найдите угол ВАD. Ответ дайте в градусах.

Ключевое слово в данной задаче – биссектриса. Вспоминаем, что она делит угол пополам. Нам надо найти величину угла ВАD, следовательно он равен половине угла ВАС, то есть 84 0 :2=42 0

pазбирался: Даниил Романович | обсудить разбор | оценить

🎥 Видео

№143. Расстояние от точки М до каждой из вершин правильного треугольника ABC равно 4 смСкачать

Вычисляем высоту через координаты вершин 1Скачать

Уравнения стороны треугольника и медианыСкачать

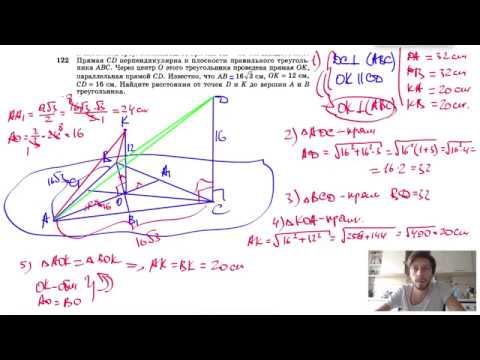
№122. Прямая CD перпендикулярна к плоскости правильного треугольника ABC. Через центр О этогоСкачать