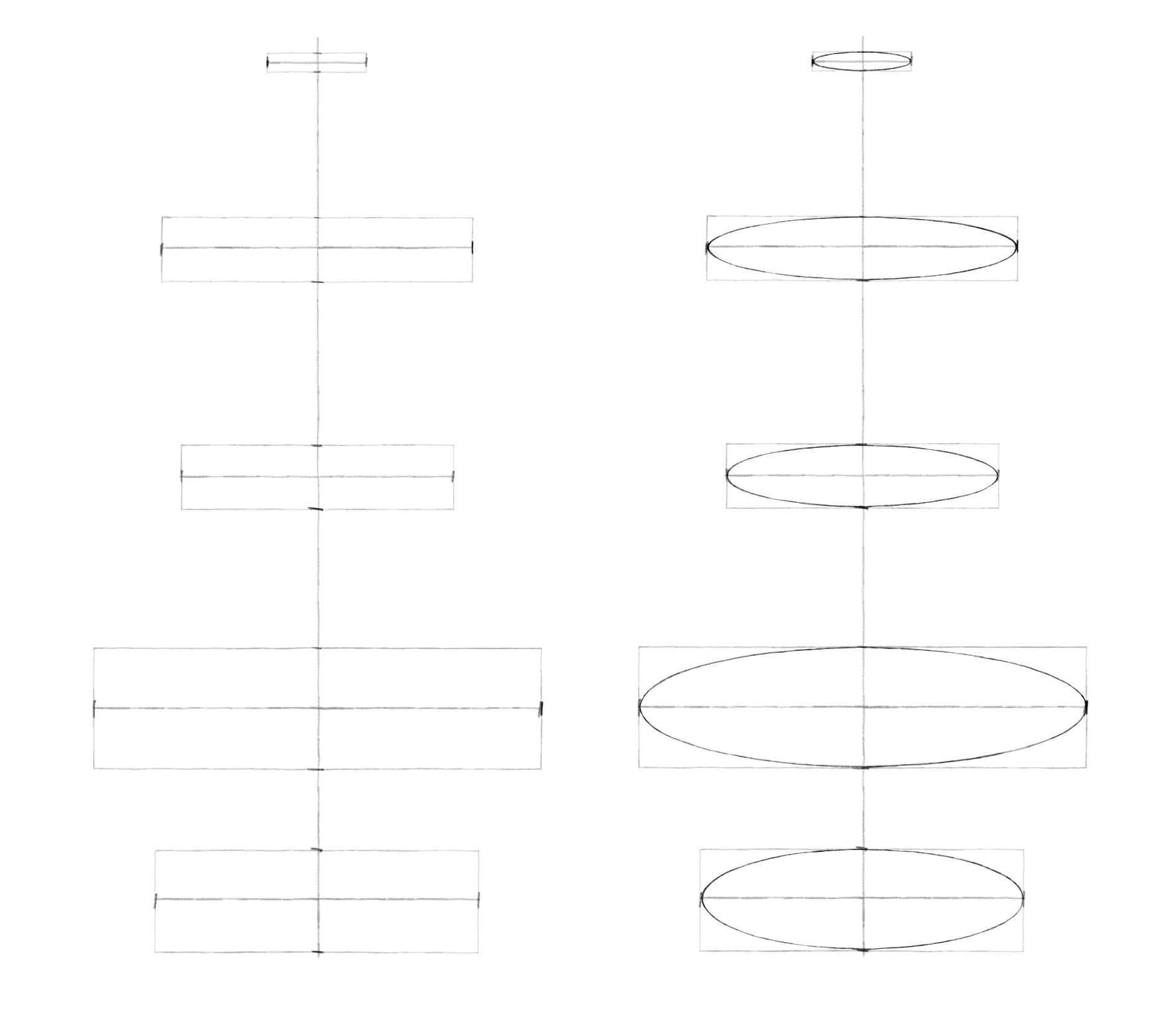
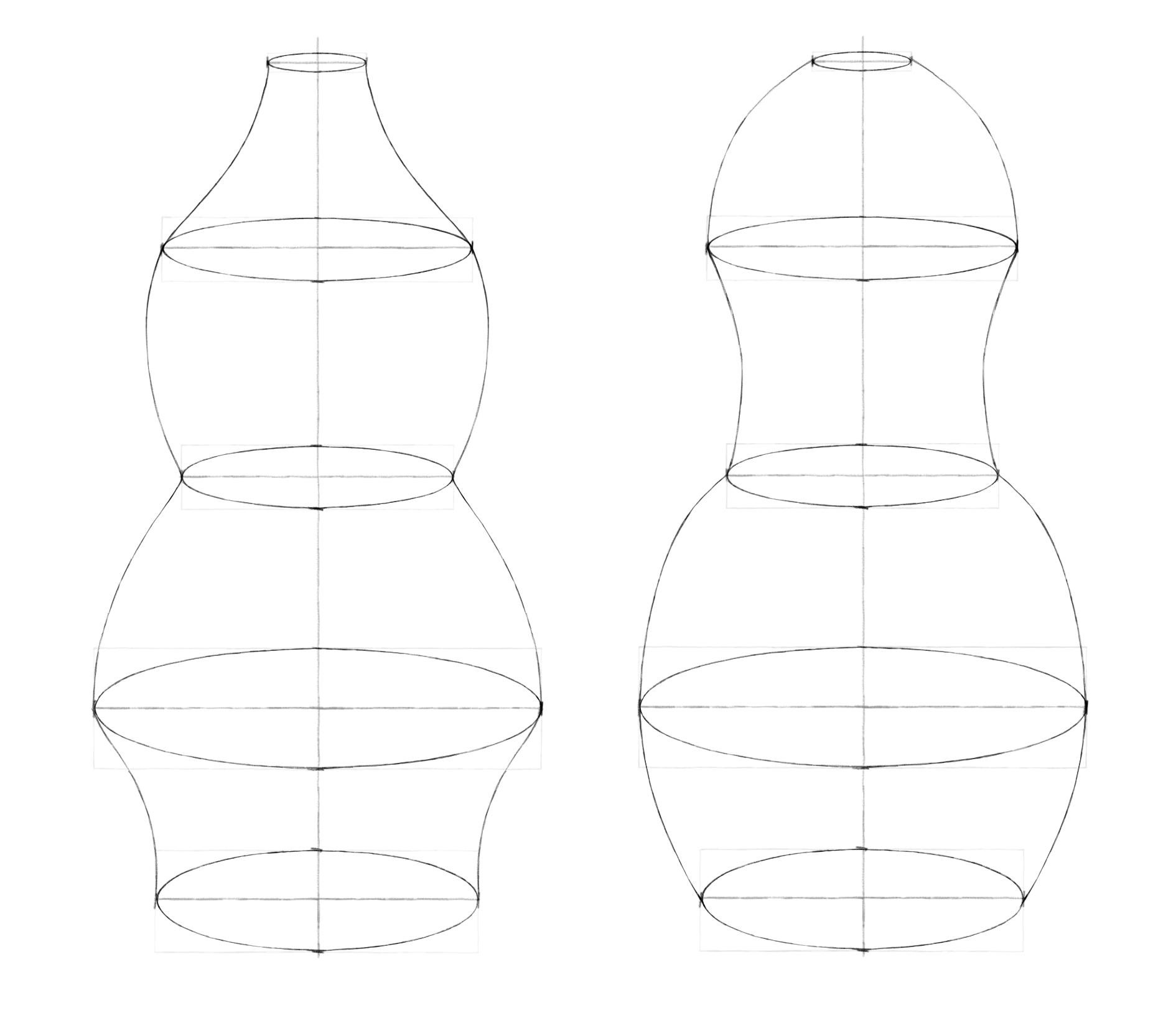
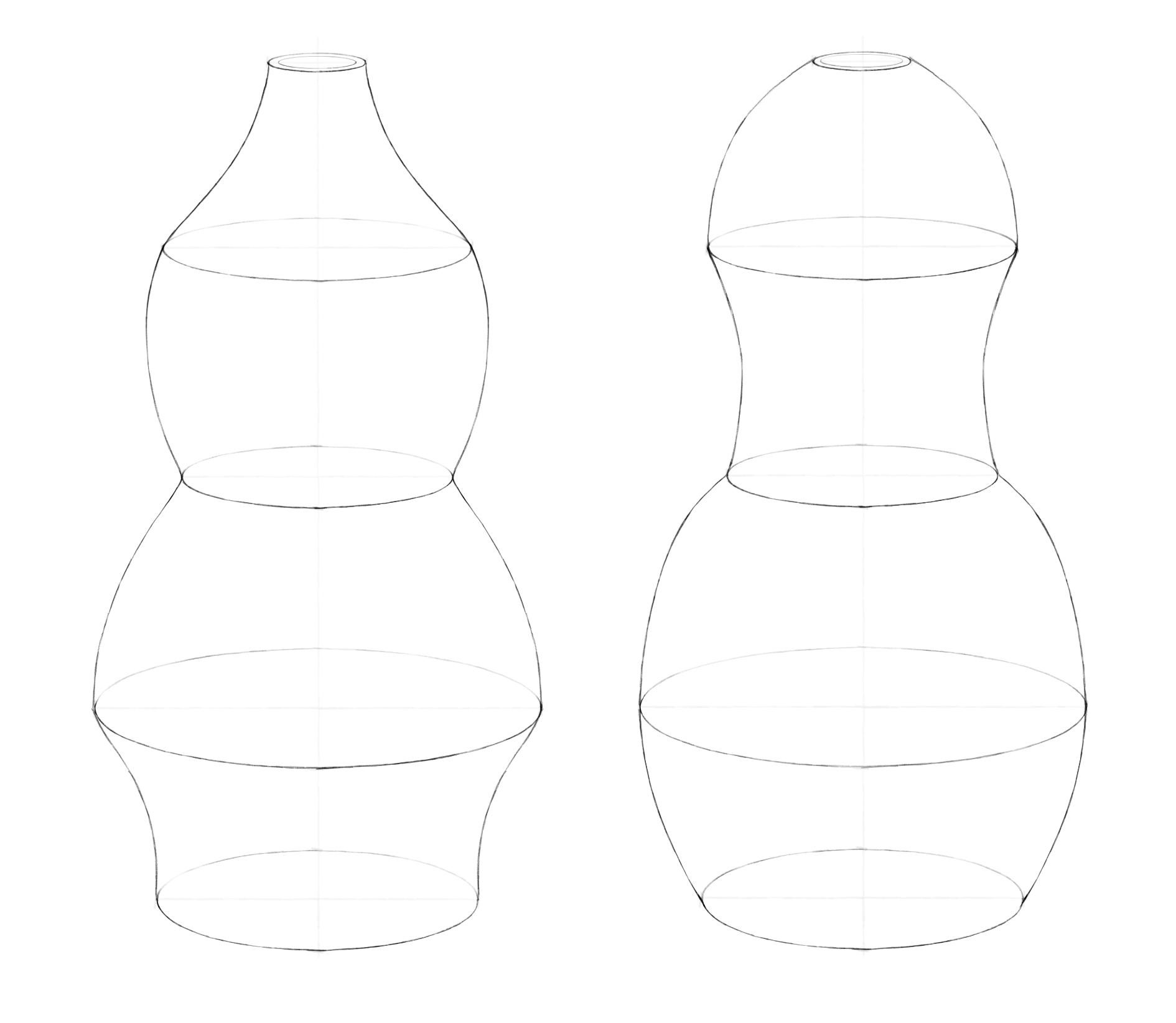
В этом уроке мы разберемся, как изображать объекты, в основе которых лежат окружности: чайник, вазу, бокал, кувшин, колонну, маяк. Сложность их изображения в пространстве заключается в том, что принцип равноудаленности точек окружности от центра срабатывает, только когда мы смотрим на плоскость прямо (то есть направление взгляда перпендикулярно ей). Например, мы видим круглый циферблат часов перед собой или чашку и блюдце, когда наклонились над ними. В других случаях (взгляд падает на плоскость под углом) мы видим искажение формы окружности, ее превращение в овал (эллипс).
Содержание:
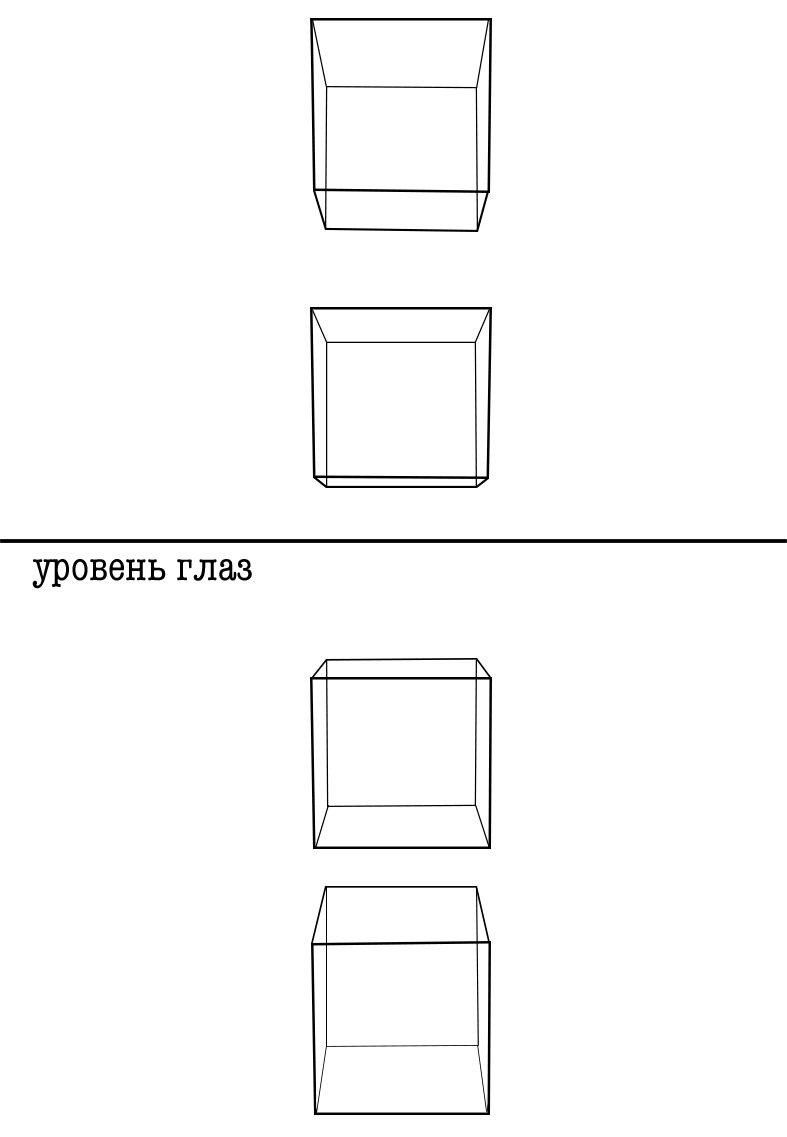
Ненадолго вернемся к коробкам из прошлого урока. Только теперь рассмотрим кубическую форму. Обратите внимание, как квадраты плоскостей, уходящих вдаль, сплющиваются. Верхние и нижние грани превращаются в трапеции. И тем сильнее они сужаются по вертикальной оси, чем ближе находятся к уровню глаз (к линии горизонта).
То же самое происходит и с окружностями. Чем дальше от линии горизонта они находятся, тем больше они открываются (обратите внимание на верхние и нижние плоскости этих спилов). А на уровне глаз окружность сужается до линии. Мы видим лишь переднюю грань предмета.
Видео:Как правильно построить квадрат в перспективеСкачать

Принципы рисования эллипсов:
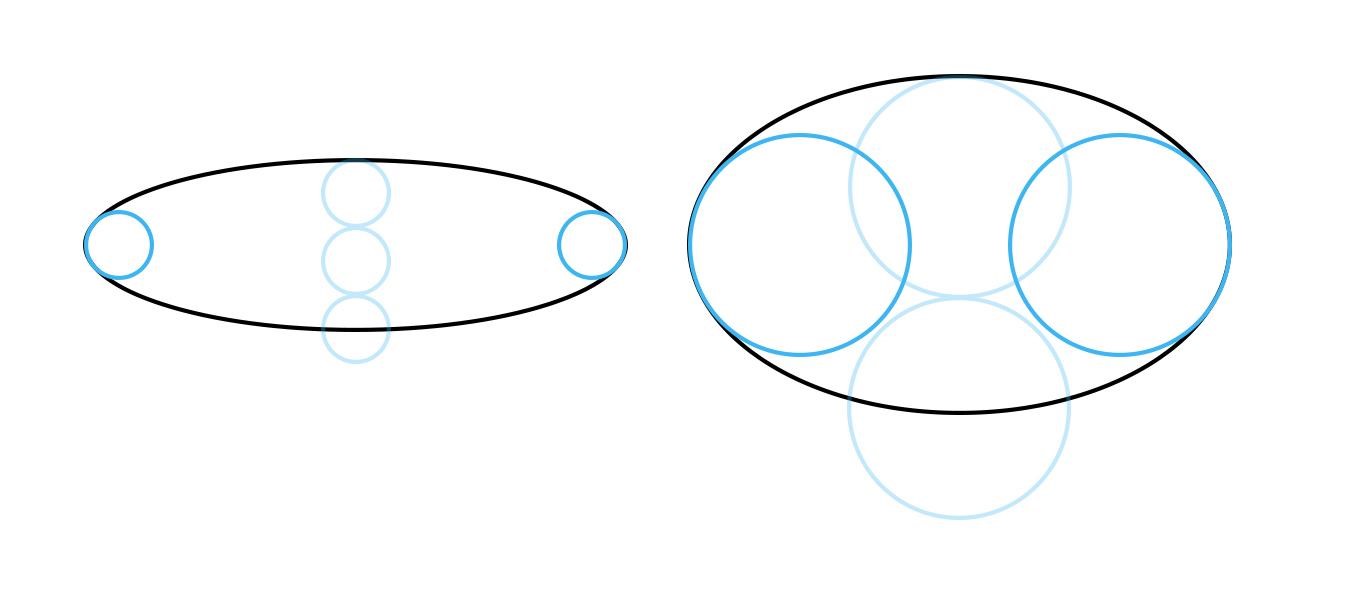
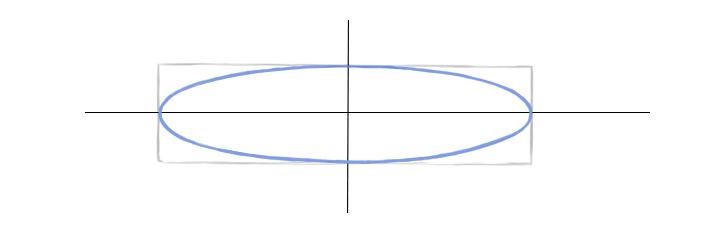
Принцип 1. У эллипса есть две оси симметрии: большая и малая. Они перпендикулярны. Здесь будем работать с наиболее частым случаем – когда предмет расположен прямо, то есть вертикальная ось (малая) находится под углом в 90°, а горизонтальная (большая) – под углом в 180°.
Принцип 2. У эллипса 4 вершины (они лежат на пересечении с осями). Эти точки в наибольшей степени удалены от центра. Форма эллипса выглядит искаженной, если соседние с вершинами точки смещены на тот же уровень (на эллипсе справа показано красным цветом).
Принцип 3. Другая крайность – это заострение боков эллипсов. Они должны быть скругленными. В бока можно вписать окружности. И чем больше раскрыт эллипс, тем больше диаметр этой окружности относительно высоты эллипса (на примере ниже это сравнение показано бледно-голубым цветом).
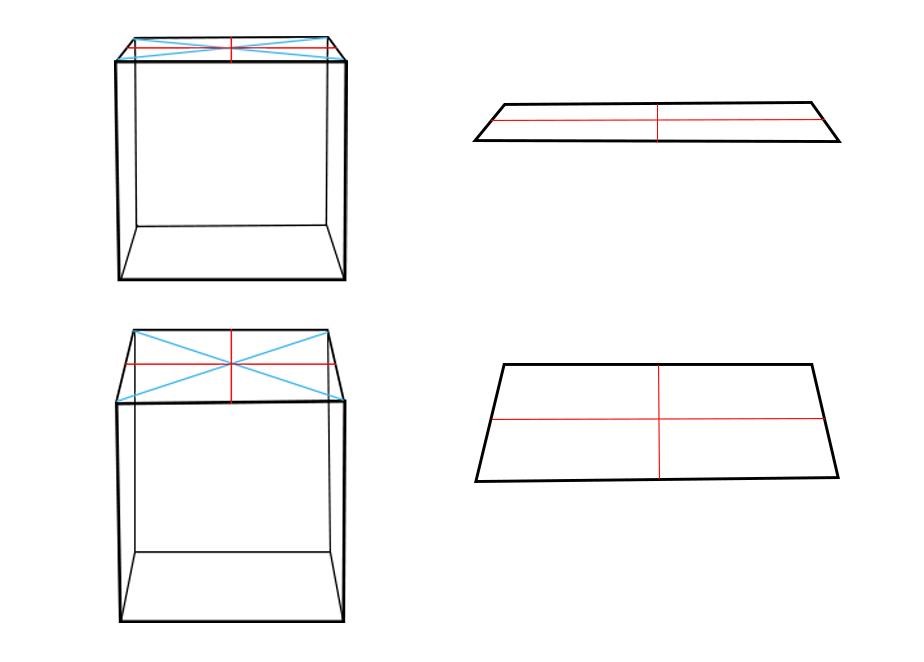
Принцип 4. Центр эллипса смещен вдаль (вверх) относительно геометрического центра из-за перспективного искажения. То есть ближняя половина эллипса больше дальней. Однако обратите внимание, что это смещение очень незначительно. Разберем, почему. Начнем с квадратов, поскольку круг вписывается в эту форму. Ниже показаны кубы, справа их верхние квадратные грани в перспективе. Проведены оси красным. Сравните, насколько их ближние половины больше дальних. Разница очень небольшая. То же самое будет и для эллипсов, вписанных в них. Ошибочно преувеличивать в рисунках эту разницу между ближней и дальней половинками эллипсов.
Видео:Изображение окружности в перспективе. Эллипс.Скачать

Рисуем эллипсы
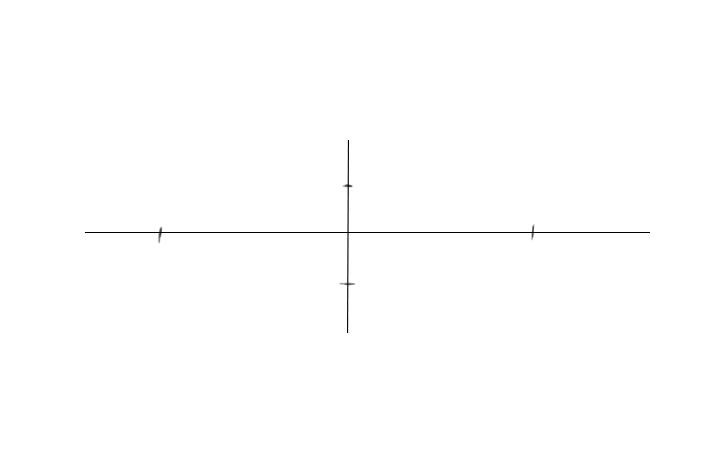
Шаг 1. Для начала проведем две перпендикулярных оси.
Шаг 2. Отметим границы произвольного эллипса симметрично по горизонтальной оси. А для вертикальной верхнюю половину (дальнюю) сделаем чуть-чуть меньше нижней.
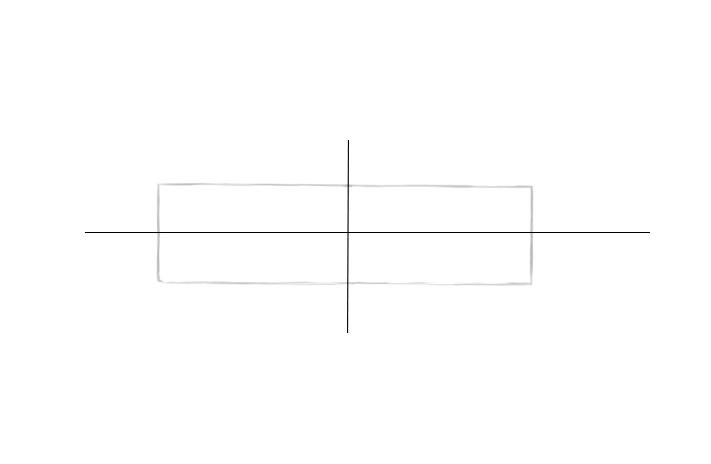
Шаг 3. Нарисуем по этим отметкам прямоугольник, в который будем вписывать эллипс.
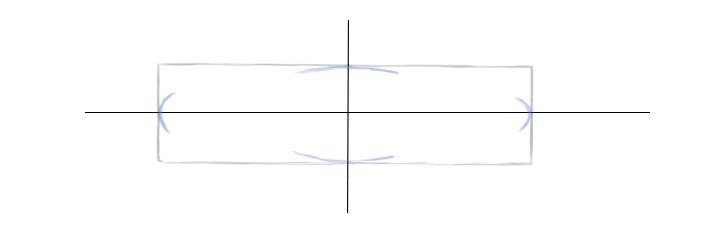
Шаг 4. Наметим легкие дуги в местах пересечения осей и прямоугольника.
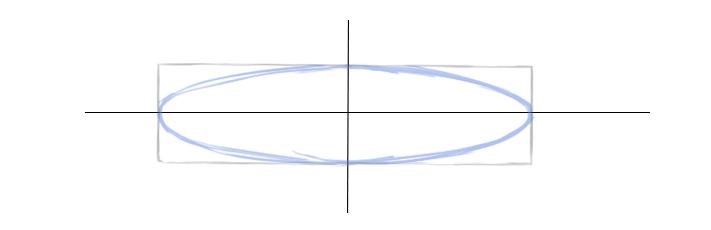
Шаг 5. Соединим легкими линиями эти дуги, стараясь изобразить эллипс более симметрично.
Шаг 6. По обозначенному пути проведем более четкую линию. Смягчим ластиком лишнее.
Более правильно было бы при рисовании эллипса вписывать его в квадратную плоскость в перспективе, то есть в трапецию. Однако, во-первых, сложно точно построить такую трапецию, зная лишь вершины эллипса. А во-вторых, овал, вписанный в квадрат в перспективе, мало отличается от вписанного в прямоугольник по тем же самым вершинам.
Видео:Круг в перспективеСкачать
Рисуем кружку
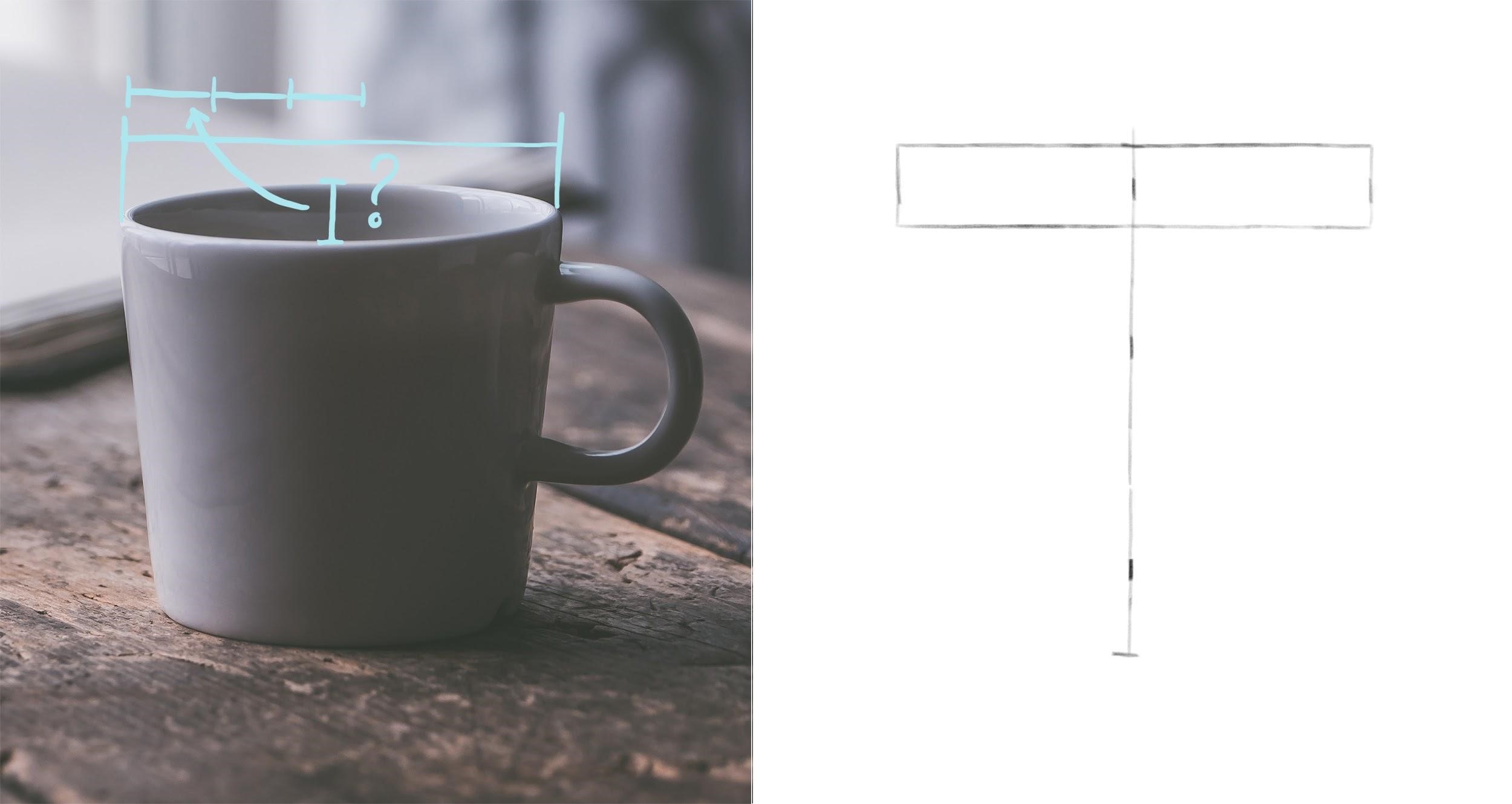
Шаг 1. Начинаем с общих пропорций предмета. Измеряем, сколько раз ширина кружки (ее верха) умещается в высоте. Можно пока не учитывать ручку, однако надо оставить для нее достаточно места на листе. Намечаем общие габариты. Находим середину предмета по ширине и проводим через нее вертикальную ось. Чтобы нарисовать ее ровно, удобно сделать 2-3 вспомогательные отметки по высоте предмета на том же расстоянии от ближнего края листа, что и первая отметка середины предмета.
Шаг 2. Найдем высоту верхнего эллипса. Для этого измерим, сколько раз она умещается в его ширине (которую мы нашли ранее). Отметим нижнюю границу эллипса от верхнего края кружки. Легкими линиями нарисуем прямоугольник по намеченным крайним точкам.
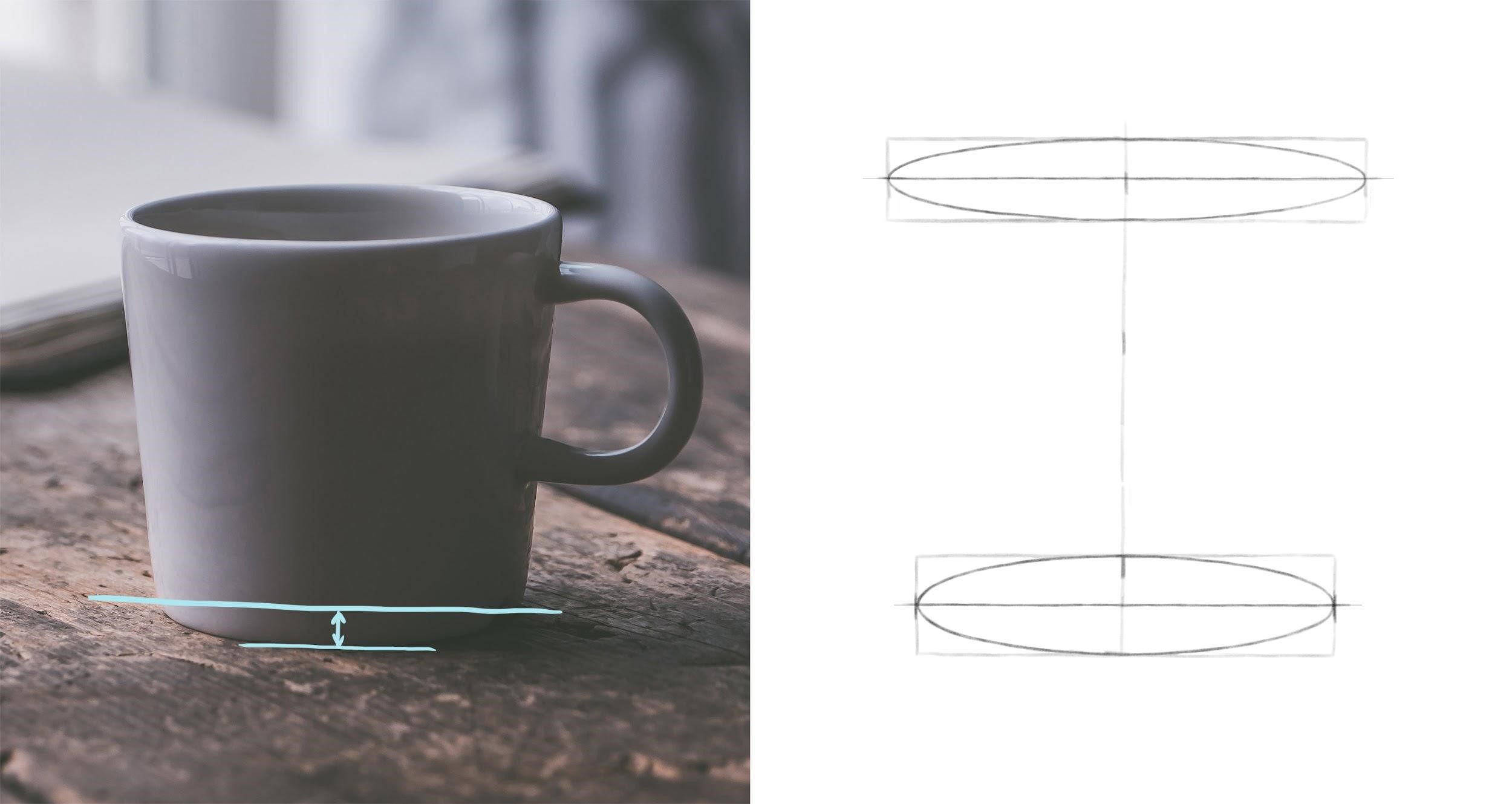
Шаг 3. Проведем горизонтальную ось и впишем эллипс в прямоугольник. Затем найдем ширину нижней части кружки, сравнив ее с шириной верха. Высоту нижнего эллипса мы найдем, измерив расстояние по вертикали от самой нижней отметки кружки до нижней отметки ее бока (до точки, через которую пройдет горизонтальная ось этого эллипса). Найденное расстояние – это половина искомой высоты. Удвоим его и отложим от самой нижней точки кружки. Здесь важно не запутаться: в данном случае ось надо провести через нижнюю точку бока кружки, а не через низ самой кружки. Иначе пропорции нарушатся. Зная высоту нижнего эллипса, проверим, соблюдается ли принцип их постепенного раскрытия по мере удаления от уровня глаз. Верхний эллипс расположен ближе к уровню наших глаз, чем нижний, поэтому должен быть уже. Найдем, сколько раз высота нижнего овала помещается в его ширине – около четырех раз. Для верхнего овала было соотношение примерно 5 к 1. Таким образом нижний овал шире, то есть раскрыт в большей степени. Принцип соблюдается.
Шаг 4. Рисуем стенки кружки, соединяя боковые вершины верхнего и нижнего эллипсов. Для большей объемности покажем толщину стенки. Нарисуем второй овал внутри верхнего. При этом учитываем, что из-за перспективного искажения толщина стенок выглядит не одинаковой. Передняя и дальняя стенки визуально сужаются сильнее боковых примерно в два раза. Отметим вершины внутреннего овала на некотором расстоянии от вершин первого овала. Делаем этот отступ чуть больше для боковых вершин. Ставим отметки симметрично относительно вертикальной и горизонтальной осей. Нарисуем новый эллипс через эти вершины.
Шаг 5. Найдем расположение ручки и ее общие пропорции, а затем схематично наметим основные отрезки, формирующие ее контур. Их наклоны определяем методом визирования (а где-то — на глаз).
Шаг 6. Уточним контур ручки, сделаем его более плавным. По необходимости подправим очертания кружки. Смягчим немного ластиком линии построения. Выделим более сильным нажимом на карандаш контуры, расположенные ближе к нам. Кружка готова!
Видео:ТЕМА 1. ОСНОВЫ ПЕРСПЕКТИВЫСкачать

Рисуем вазу
В этом упражнении поработаем с воображением. Придумаем свою вазу и потренируемся рисовать эллипсы.
В прошлом задании для построения кружки было достаточно нарисовать два эллипса. Две ключевые окружности (верхняя и нижняя) определяли ее форму. Диаметр кружки равномерно уменьшался от верха к низу. А, например, форма вазы из рисунка ниже зависит от четырех окружностей (причем верхняя находится на уровне глаз, поэтому превратилась в линию).
Перейдем к рисованию. И помним важный принцип: чем дальше эллипс от уровня глаз, тем более он раскрыт.
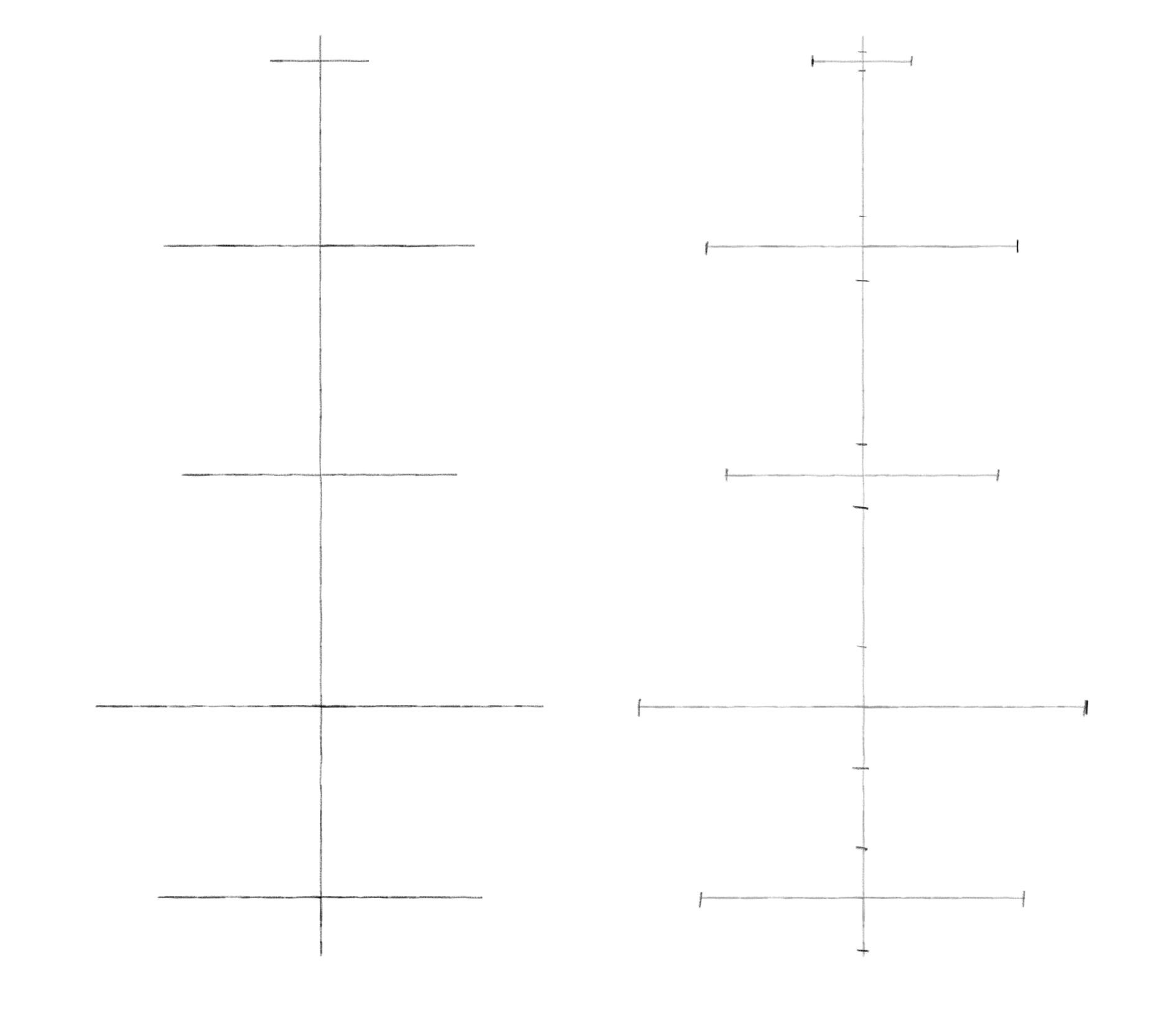
Шаг 1. Проведем вертикальную ось. От нее симметрично отложим горизонтальные оси будущих эллипсов. Длину вертикальной и горизонтальных осей, а также количество эллипсов и расстояние между ними выбирайте сами.
Шаг 2. Обозначим боковые вершины эллипсов симметрично относительно вертикальной оси. Теперь перейдем к обозначению верхних и нижних вершин. И здесь пользуемся принципом постепенного раскрытия эллипсов по мере удаления от линии горизонта. Например, здесь мы рисовали вазу, расположенную в целом ниже уровня глаз. Для первого эллипса взяли высоту, примерно в пять раз меньше ширины. Измеряли это карандашом. Для последующих эллипсов постепенно увеличивали степень раскрытия. Так высота среднего эллипса укладывается в ширине примерно четыре раза, а для самого нижнего – примерно три раза. Чем ближе друг к другу эллипсы, тем ближе они по степени раскрытия. Чем дальше – тем больше разница. Намечая вершины, нижнюю половинку (ближнюю) делаем чуть-чуть больше верхней (дальней).
Шаг 3. Через вершины легкими линиями рисуем прямоугольники. А затем вписываем в них эллипсы.
Шаг 4. Теперь самое интересное: надо соединить боковые вершины эллипсов линиями. Вам решать, какими они будут, прямыми или округлыми, вогнутыми или выпуклыми. Можно сделать пару вариантов. Постарайтесь наиболее симметрично повторить форму внешнего контура для двух половинок вазы. Чтобы проверить симметрию, пробуйте перевернуть работу вверх ногами. Взглянув на предмет по-новому, проще увидеть расхождения.
Шаг 5. Так же, как мы делали для кружки, здесь можно показать толщину стенки. Нарисуем внутри верхнего эллипса еще один поменьше, предварительно наметив его вершины. Смягчим ластиком оси и дальние половинки эллипсов. Можно чуть высветлить те эллипсы, в которых изменение формы вазы более плавное. Рисунок готов!
Видео:Перспектива: квадрат, круг, овал и эллипс.Скачать

Проверьте свои знания
Если вы хотите проверить свои знания по теме данного урока, можете пройти небольшой тест, состоящий из нескольких вопросов. В каждом вопросе правильным может быть только 1 вариант. После выбора вами одного из вариантов, система автоматически переходит к следующему вопросу. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что вопросы каждый раз разные, а варианты перемешиваются.
Напоминаем, что для полноценной работы сайта вам необходимо включить cookies, javascript и iframe. Если вы ввидите это сообщение в течение долгого времени, значит настройки вашего браузера не позволяют нашему порталу полноценно работать.
Видео:КАК РИСОВАТЬ ЭЛЛИПСЫ. Простой и быстрый способ рисования ЭЛЛИПСОВСкачать

Рисование круга, квадрата в перспективе
Нарисовать круг, квадрат в перспективе карандашом на листе бумаги формата А4.
Только при рассматривании сверху граница круга близка к окружности. При всяком же другом положении граница круга будет иной замкнутой кривой, напоминающей овал (но отнюдь не овал!). В этом легко убедиться, если взять три тарелки, одну из них положить около ног на пол, другую — на стул, а третью — на стол в 2—3 м от ваших глаз. Промерьте карандашом на вытянутой руке длину и ширину «овала» тарелки на стуле и на столе. Чем ниже располагается тарелка, тем круглее «овал», а чем ближе к уровню ваших глаз, тем он более сжат сверху вниз. На уровне ваших глаз «овал» становится прямой горизонтальной линией.
Слово «овал» мы все время берем в кавычках, потому что перспективное изменение круга — вовсе не овал, в чем также не трудно убедиться. Посмотрим на рисунок 1.
Рисунок 1 — Вверху круг, вписанный в квадрат; внизу тот же квадрат и круг в перспективном изображении.
Вверху изображен круг, вписанный в квадрат. Через центр круга проведены два диаметра, перпендикулярные к сторонам квадрата. Внизу тот же круг в перспективном изображении. Но как изобразить круг в перспективе? Это легко понять, если обратиться к нашей перспективной сетке.
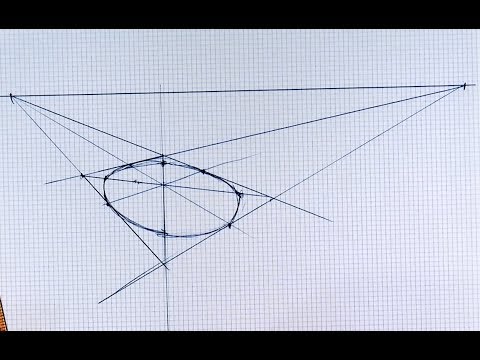
Берем на перспективной сетке 4 квадрата (сначала в середине). Эти квадраты дают нам представление об изменении нашего квадрата со вписанным в него кругом. Попробуем «вписать» круг в квадрат пашей сетки. При некотором терпении, размышлении (а еще лучше при рассматривании тарелки на стуле) это не трудно сделать (рис. 2).
Рисунок 2 — Построение перспективы круга.
Проанализируем полученный рисунок. Круг в перспективе стал иной замкнутой кривой, похожей на «овал». Обратите внимание на радиусы АС и СВ. АС от нас дальше, чем СВ, и потому он кажется короче. Последнее вы можете на чертеже проверить циркулем или полоской бумаги. Это обстоятельство необходимо хорошо запомнить. Когда нам придется где-либо изображать круг с натуры (мы имеем в виду круг, расположенный перед нами на плоскости, уходящей от нас в ту или другую сторону), мы тщательно измеряем высоту видимого «овала» и намечаем приблизительное место будущего рисунка на листке. Потом проводим горизонтальную линию и отмечаем ширину будущего рисунка круга. Делим эту ширину на две части и проводим через середину вертикальную линию, на которой должны изобразить «высоту» видимого «овала». Гут мы должны внимательно посмотреть и проверить, какой длины ближайший к нам отрезок «высоты» и на сколько он больше второго, дальше отстоящего, отрезка. А что ближний отрезок больше дальнего, это мы хорошо знаем и постараемся никогда не забывать.
Дальше уже все зависит от практики. Чем больше будет упражнений, тем вернее глаз будет схватывать размеры отрезков и рука правильнее передавать окружность, измененную перспективой. В дальнейшем вы сразу будете изображать перспективные изменения окружности без всяких измерений. Но это будет после длительных и разнообразных упражнений.
Здесь необходимо еще предупредить одну характерную для начинающих ошибку. Многие думают, что при изображении круга в перспективе можно ограничиться дугами двух окружностей различных радиусов (рис. 3). Эту же ошибку довольно часто допускают и хорошие чертежники. Из приведенного рисунка легко видеть, что при таком способе изображения получается не окружность в перспективе, а сломанная окружность. Посмотрите в натуре на тарелку, отверстие стакана — там нет сломанной окружности. Там переход плавный и округленный.
Научиться проверять правильность квадрата, вписывая в него окружность.
Изобразите в перспективе горизонтальный и вертикальный квадраты. Проверьте правильность их изображения при помощи вписанных окружностей.
Прежде, чем приступать к выполнению этого задания, внимательно рассмотрите схему на рис. 2.8. Точки касания сторон квадрата к окружности (точки 1, 2, 3, 4) делят стороны квадрата пополам. Средние линии квадрата и его диагонали пересекаются в центре окружности. Противолежащие стороны квадрата и соответствующие им средние линии параллельны и расположены на равном расстоянии друг от друга. Рассмотрите также рис. 2.9. На примере окружности и квадрата во фронтальной перспективе хорошо видно, что центр эллипса и центр окружности — две разные точки. Диаметр окружности, являющийся малой осью эллипса, делится точкой центра окружности на два разных по величине отрезка: ближний к зрителю — больше, дальний — меньше (по закону перспективного сокращения), а точка центра эллипса делит этот же диаметр — малую ось эллипса — ровно пополам.
Рисунок квадрата в перспективе
Рисунок квадрата в перспективе
Нарисовать квадрат в перспективе можно в разной последовательности, например, сначала изобразить одну прямую — сторону квадрата, а затем другую, ей перпендикулярную, отложить на этих прямых от точки их пересечения отрезки, равные стороне квадрата, а затем от полученных вершин достроить остальные стороны, сводя параллельные прямые в точки схода. Или иначе — сначала провести две параллельные прямые, а затем еще две, перпендикулярные двум первым. В любом случае эта задача кажется простой только на первый взгляд. На самом деле слишком много позиций (степень схождения параллельных сторон квадрата, их направления и размеры) рисовальщику приходится определять на основании своего личного опыта, а его, как известно, иногда бывает недостаточно. Именно поэтому правильность квадрата необходимо проверить, например, вписав в него окружность. При любом положении квадрата для того, чтобы вписать в него окружность (в перспективном рисунке — эллипс), необходимо найти точки касания сторон квадрата к вписанной окружности (точки 1 — 4) и определить положение осей эллипса. Если вписанный эллипскасается сторон квадрата в заданных точках и симметричен относительно осей, то квадрат нарисован верно.
Горизонтальный квадрат. Нарисуйте горизонтальный квадрат по представлению (рис. 2.10). Найдите точки касания, для этого через точку пересечения диагоналей проведите прямые, параллельные сторонам квадрата и уходящие с ними в одну точку схода (рис. 2.11). Окружность, лежащая в горизонтальной плоскости, изображается на перспективном рисунке в виде эллипса с вертикальной и горизонтальной осями. Проведите через точку пересечения диагоналей вертикальную линию — малую ось эллипса. Большая ось эллипса перпендикулярна малой оси и проходит через точку, смещенную от пересечения диагоналей квадрата (центра окружности) ближе к зрителю (рис. 2.12). Таким образом, мы получили две оси эллипса и четыре точки, определяющие его габариты. Продолжите рисунок: сначала легкими движениями карандаша наметьте эллипс, затем уточните линию, добиваясь того, чтобы она действительно касалась сторон квадрата в точках 1, 2, 3, 4 (рис. 2.13). Проверьте симметричность полученного эллипса относительно его осей.
Вертикальный квадрат. При вертикальном положении квадрата точки 1, 2, 3, 4 найдите, как и в предыдущем примере: проведите через точку пересечения диагоналей квадрата прямые, параллельные его сторонам (рис. 2.14).
Рисунок квадрата в перспективе
Несколько сложнее определить направление осей эллипса. Чтобы это сделать, представьте, что изображаемый эллипс является основанием цилиндра, лежащего на горизонтальной плоскости (рис. 2.15). Ось цилиндра на перспективном рисунке всегда перпендикулярна большой оси эллипса основания и совпадает с его малой осью. Проведите ось цилиндра через точку пересечения диагоналей квадрата. Направление этой оси можно определить, опираясь на опыт рисунка с натуры. Задача значительно упрощается в том случае, если вертикальный квадрат, в который вы вписываете окружность, является гранью куба. Тогда ось цилиндра (она же малая ось эллипса) параллельна горизонтальным ребрам куба и на рисунке идет с ними в одну точку схода. Таким образом, мы определили положение малой оси эллипса. Большая ось будет ей перпендикулярна и пройдет через центр эллипса, смещенный от пересечения диагоналей (центра окружности) ближе к зрителю (рис. 2.16). На двух осях и по четырем точкам касания изобразите эллипс (рис. 2.17).
На рисунках, иллюстрирующих последовательность вписывания окружности в горизонтальный и вертикальный квадраты, представлены идеальные ситуации. В действительности эллипс, вписанный в квадрат, часто получается несимметричным относительно осей, а потому его приходится уточнять и, как следствие, изменять очертания квадрата. В этом случае работа идет как бы методом последовательных приближений и уточнений, что трудно и долго. Часто на рисунках остаются не вполне правильные квадраты и не вполне правильные эллипсы, а лишь фигуры, близкие к ним.
Правильный эллипс нарисовать легче, чем построить правильный квадрат в перспективе. Именно поэтому современная методика предлагает не проверять и исправлять подобным образом уже нарисованные квадраты, а строить их, описывая вокруг окружности.
Вид контроля: Демонстрация рисунка круга и квадрата.
Видео:Построение круга в перспективеСкачать

Линейная перспектива в рисунке
Вспоминаем глазомер
Прежде чем начать изучать, что же это все-таки такое – линейная перспектива – нужно вспомнить такое понятие как глазомер. Но, если вдруг вы не можете найти расшифровку этого термина у себя в голове, и в мысли настойчиво лезут образы всяких железяк из области хирургии – не страшно.
Вы всегда можете это исправить, то есть прочитать, что за страшный инструмент-то такой – этот глазомер.
Возвращаясь к понятию о перспективах, его (глазомер) можно представить как наблюдательную перспективу. Но чтобы обладать феноменально точной наблюдательной перспективой, нужно слегка ознакомиться (ну ладно, не совсем слегка) с законами линейной перспективы, которая является кусочком той самой геометрии, которую многие совершенно не любят еще со времен школы – по себе знаю.
Все, что видят наши глаза, на самом деле предстает перед ними в искаженной форме (да-да, это так), ведь иначе им было бы сложно увидеть и заметить все, согласитесь. Но это еще не значит, что вещи, пейзажи, люди и все остальное (котики, собачки, мышки и даже муравьи), на самом деле терпят изменения – они не меняются. Но мы видим перемены. Эти перемены отображаются и на рисунках.
Знаете, с чем это связано? Ни за что не поверите – все с той же перспективой, а вернее перспективным соотношением форм. Ну вот, к примеру, мы ни за что не сможем перенести на бумагу, скажем, закатный горизонт посреди цветущего поля во всем его объеме и размерах. Зато мы можем уменьшить его, и за счет искажения все же изобразить.
То есть, по сути, линейная перспектива – это способ создать пространство на плоскости листа. Но мало просто знать законы и принципы этой перспективы. Это как раз тот самый случай, когда нужно понимать и уметь этим пользоваться.
Здесь не прокатит, как в математике: я запишу, вызубрю и буду классным художником. Нет, здесь можно и не вызубривать, главное, понимать применение.
Ваш глазомер без понимания этих законов и принципов будет как… ну, скажем, часы без стрелок. Они ведь идут, верно? Но времени мы не знаем. Так и здесь: вы сможете рисовать, но рисунки все равно будут… неестественными. Слепое копирование – вот то, как это можно назвать. А вы ведь хотите рисовать по-настоящему?
Давайте потихоньку разбираться с понятием линейной перспективы – знаю, вам уже очень не терпится это сделать. Для начала предлагаю увидеть ее в действии. Для этого вам нужно немного отвлечься от экрана и посмотреть в разных направлениях – просто посмотреть, не вставая с насиженного удобного стула – на стену слева, на замечательную люстру сверху, на классический шкафчик в конце комнаты, на входную дверь…
Можете также глянуть в окно — там без сомнения вы тоже увидите много чего, начиная от деревьев и заканчивая домами. Так вот, все это поддается кажущимся (эдаким «псевдо») изменениям, в виде уменьшения и сокращения.
Например, мы же знаем, что вон то дерево или тот дом ни в коем случае не поместится у нас в руке, но, тем не менее, мы свободно можем одной ладонью спрятать его от глаз. Это уменьшение видимого настолько привычно для нас, что в повседневной жизни мы даже и не замечаем его. Я веду это к тому, что нашим основным и важнейшим заданием является научиться переносить то, что мы видим, на бумагу, причем в соответствии с нашим видением и восприятием – переносить это убедительно.
Ну вот, мы и подобрались к практической части освоения линейной перспективы. Приготовьте карандаш (или ручку, или фломастер, или мелок, или маркер – да все, что может по праву считаться пишущим), бумагу любого формата (вроде листочка из старой тетради по алгебре, истории или что там еще найдется – желательно, конечно взять альбомный листик), не забываем также и про ластик (ну или же промокашку).
Если вы из талантливых, но не хотите особо тратиться – используйте кусочек кирпичика и любую бетонную поверхность (а что, тоже вариант…)
Приготовили? Отлично, теперь сочувствующие окиньте взглядом несчастный листик и приступайте к работе.
Перспектива квадрата

Квадрат готов, можно даже несколько секунд полюбоваться его идеальностью. Полюбовались?А теперь продолжим.
Сейчас нам нужно дорисовать так называемую линию горизонта. В геометрии (коей мы сейчас и занимаемся) эта линия обычно задается, поэтому рисуем ее на произвольном расстоянии от нашего гениального квадрата. Но вообще принято считать, что линия горизонта находится на уровне ваших глаз.
Определить ее можно с помощью стакана воды: берете стакан, наливаете до половины воду и водите им перед глазами – то место, где ваш взгляд и линия уровня воды в стакане встретятся напрямую, и будет считаться линией горизонта.
Дальше у нас по плану новый монстр – это точка схода. Такой точкой называется место на линии горизонта, где сталкиваются все параллельные грани рисуемого предмета (в нашем случае квадрата). Чтобы было проще, впихнем нашу точку схода прямо перед нашим квадратом – выходит, что мы словно смотрим напрямую в «лицо» квадрата.
Чтобы определить уровень точки схода на линии горизонта, нам нужно перечеркнуть квадрат – но аккуратно так перечеркнуть, диагоналями из угла в угол. На месте, где пересекутся эти самые диагонали, проводим не менее аккуратный перпендикуляр к самой линии горизонта. И кто это тут у нас? А это у нас точка схода. Мы нашли ее.
Дальше совсем уж просто… Берем уголочки квадрата и соединяем их линиями в точке схода.
Теперь займемся превращением простого квадрата в совершенно простой куб (рисунок справа). Для этого нам нужно найти заднюю грань куба – такой небольшой отрезок, который мы назовем… пусть будет А-Б. В геометрии его обычно высчитывают, но мы же с вами не математики, верно? Потому сейчас мы определим его, положившись на ощущение, а в дальнейшем – глазомер вам в помощь.
Теперь уж совсем просто дорисовать оставшиеся задние грани и – браво! – у нас вышел замечательный куб (рисунок слева), выстроенный по законам той самой непонятной штуки, именуемой как линейная перспектива. И даже без применения глазомера.
Но так легко и просто можно нарисовать перспективу только там, где мы смотрим в лоб, то есть, если рисуемый предмет находится прямо напротив нас. Если же мы сдвинемся в сторону или того круче, отойдем в левую сторону (или вправо) от изображаемого предмета, то картинка совершенно изменится, а самое главное изменится точка схода. Более того, их станет две, ведь нам нужно будет учитывать еще и обе стороны куба – как правую, так и левую.
Давайте попробуем отодвинуться от нашего воображаемого куба чуток влево и постепенно нарисовать то, что выйдет.

Точки находятся на неравноправном расстоянии от квадрата и одна из них будет ближе, а другая, соответственно, дальше.
Согласно законам линейной перспективы, это расстояние задается размерами изображаемого предмета, определяется ими. Но наш будущий куб существует только у нас в голове, а, значит, и определять мы его будем по ощущению – на свой вкус, так сказать.
Оставшиеся линии достраиваем так, как и в предыдущем случае.
В построении этого куба нам очень помогли перспективные построения (ну все эти линии горизонта, точки схода и прочие отрезочки). Но не забывайте, это ведь часть математики, а мы ведь творим, верно? И именно поэтому перспективным построениям нет места в рисовании – в конце-концов, это же творческий процесс, создание пространства на листике бумаги, а не какое-то там сухое черчение.

Если внимательно рассмотреть рисунки, поданные выше, то можно заметить, как именно взаимодействует глазомер и линейная перспектива. Сначала, с помощью наблюдательной перспективы (то есть глазомера) определяем основные размеры и величины (то есть углы, расстояния между гранями, повороты, соотношения сторон и, самое главное, положение рисунка на листе). А уже линейная как бы подтверждает эти определения и при необходимости корректирует их.

Со временем и достаточным упорством в тренировках, думаю, не сложно будет переместить понятие перспективы в воображение и уже оттуда ею управлять.
Для того, чтобы это не было проблемой, как уже было сказано ранее, нужно упорство в тренировке вашего глазомера. К примеру, вы можете попробовать нарисовать еще несколько перспектив, меняя взгляд на него, то есть угол, с которого вы будете его рисовать – слева-сверху, справа-снизу и так далее. Это даст вам возможность увидеть перемены в предмете на картинке.
Цилиндр в перспективе
Если вы все еще здесь, а не бросились оттачивать свой глазомер, тогда давайте посмотрим, как же будет вести себе еще цилиндр, нарисованный в перспективе (см. рисунок слева) .
А сейчас большая пребольшая тайна: любой цилиндр можно вписать в прямоугольник. Из этого следует, что форма окружностей нашего цилиндра целиком и полностью зависит от формы этого самого прямоугольника, в который он вписывается. То есть, окружность нашего цилиндра нужно будет выстраивать, базируясь на основаниях и верхушках прямоугольника. Но, опять-таки, вернемся к схеме-рисунку: красным цветом выделена кривая, что лежит в основе построения и определяется снова таки нашим глазомером.
Если у вас еще не пропало желание оттачивать рисование в перспективе, тогда респект вам и уважение. Предлагаю, наконец-то, приступить к тренировке и порисовать объемные формы – любые, на ваше усмотрение. И не забывайте, стоит только изменить линию горизонта, как вместе с тем меняется и весь рисунок – начиная от граней и заканчивая уголками.

Напоследок несколько идей, на рисовании чего можно было бы оттачивать это понимание:
- Кухонная утварь (столы, стулья, плита, шкаф… старого кота, дремлющего на подоконнике, рисовать не обязательно).
- Мебель (в случае если у вас есть лабрадор – он в данной ситуации мебелью не считается).
- Геометрические фигуры в перспективе.
- Наброски улицы. Можно рисовать как отдельные строения, так и всю улицу (включая автомобили, дороги и прочее). Не обязательно срисовывать каждую деталь, главное – отыскать искажения и изобразить их.
Следующий урок: Палитра цветов
🎥 Видео
Урок 3. Окружность в перспективеСкачать

Вписанная и описанная окружность - от bezbotvyСкачать

Перспектива. Метод архитекторовСкачать
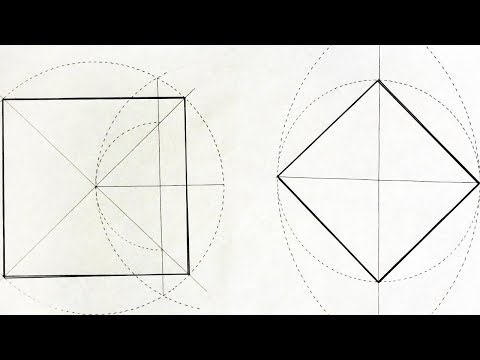
Вся правда об эллипсах!Скачать

УРОК 1.КАК НАРИСОВАТЬ КУБ.Академический рисунок.Перспектива.Рисунок карандашом.Скачать

Как построить квадрат, два способаСкачать
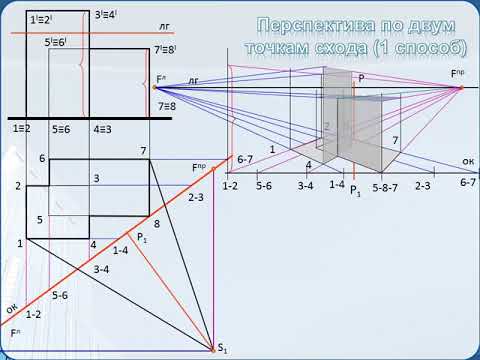
НГ Перспектива вертикальной окружностиСкачать

Уроки рисования. Как рисовать перспективу. Линейная перспектива. Учимся перспективе за 15 минут.Скачать

Перспектива. Построение окружности в перспективе.Скачать

Как БЫСТРО научиться рисовать⁉️ 3 БАЗОВЫХ УПРАЖНЕНИЯ ✔️ - А. РыжкинСкачать

Аксонометрические Проекции Окружности #черчение #окружность #проекции #изометрияСкачать

Рисую карандашом квадрат в перспективеСкачать

Угловая перспектива. Принцип построения окружности в угловой перспективе.Скачать