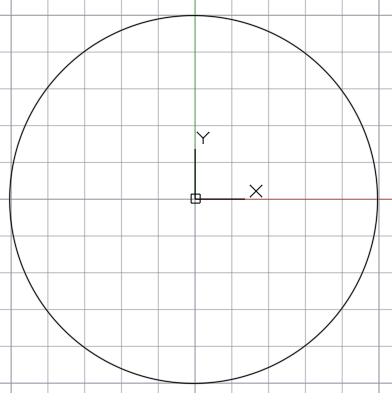
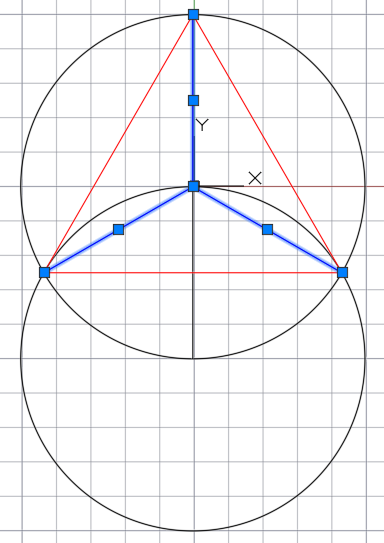
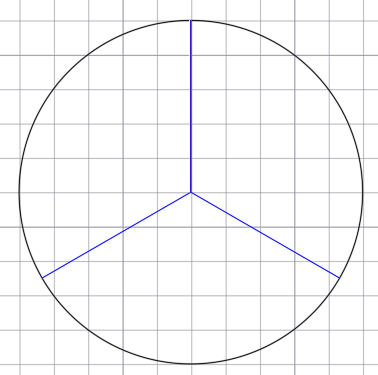
Разделить окружность на 3 части линейкой (3 видео)

Деление окружности на 3 равные части

Чтобы разделить окружность на 3 равные части, воспользуемся для этого циркулем. Итак, чертим окружность.

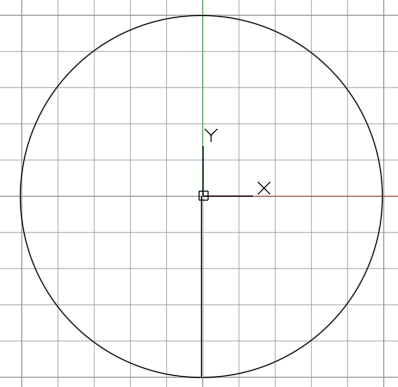
Линейкой от центра под углом 90 0 проводим линию (радиус окружности) к нижней части дуги окружности.

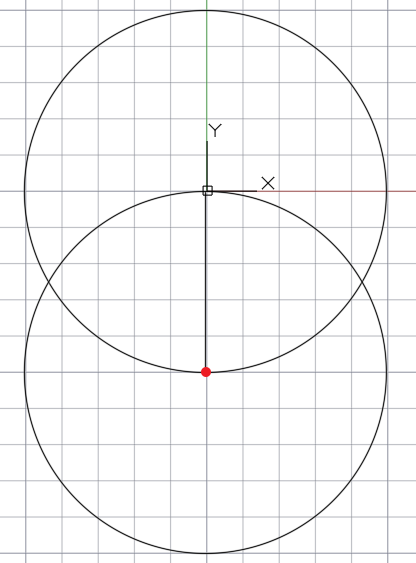
Затем место пересечение радиуса и дуги окружности — это центр новой окружности с таким же радиусом. Опять циркулем чертим окружность.

Две точки пересечения окружностей и точка, образованная пересечением радиуса (проведённого линейкой от центра первой окружности под углом 90 0 к верхней части дуги первой окружности).

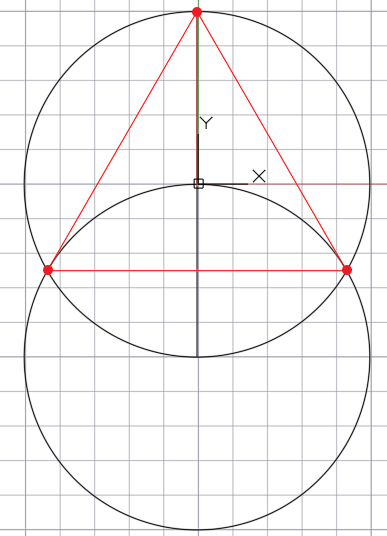
По сути, получаем треугольник.

Далее от центра первой окружности проводим линии к вершинам треугольника, тем самым делим первую окружность на три равные части под углом 120 0 .

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 4.6 / 5. Количество оценок: 37

Содержание

Деление окружности на любое число равных частей
Термины при построениях окружности
Деление окружности на 4 и 8 одинаковых частей
Деление окружности на 3 и 6 равных частей (кратные 3 трём)
Деление окружности на 5 и 10 равных частей
Деление окружности на N-ное количество одинаковых частей (построение правильного многоугольника с N сторон)
Нахождение центра дуги окружности
Покажите приемы деления окружностей на 3,6,12 частей с помощью циркуля, линейки и угольника
📸 Видео

Видео:Деление окружности на 3; 6; 12 равных частейСкачать

Деление окружности на любое число равных частей

Как разделить окружность на заданное количество одинаковых частей, терминология при построении окружности, деление окружности на 3, 4, 5, 6, 8, 10 частей.

Термины при построениях окружности

Окружностью называется замкнутая кривая линия, каждая точка которой расположена на одинаковом расстоянии от одной точки О, называемой центром.

Прямые линии, соединяющие любую точку окружности с её центром, называют радиусами R.

Прямая АВ, соединяющая две точки окружности и проходящая через её центр О, называется диаметром D.

Части окружностей называются дугами.

Прямая СD, соединяющая две точки на окружности, называется хордой.

Прямая МN,которая имеет только одну общую точку с окружностью называется касательной.

Часть круга, ограниченная хордой СD и дугой, называется сигментом.

Часть круга, ограниченная двумя радиусами и дугой, называется сектором.

Две взаимно перпендикулярные горизонтальная и вертикальная линии, пересекающиеся в центре окружности, называются осями окружности.

Угол, образованный двумя радиусами КОА, называется центральным углом.

Два взаимно перпендикулярных радиуса составляют угол в 90 0 и ограничивают 1/4 окружности.

Видео:Деление окружности на 3 частиСкачать

Деление окружности на 4 и 8 одинаковых частей

Проводим окружность с горизонтальной и вертикальной осями, которые делят её на 4-ре равные части. Проведённые с помощью циркуля или угольника под 45 0 , две взаимно перпендикулярные линии делят окружность на 8-мь равных частей.

Видео:🧭Как разделить круг на ТРИ Части, без Линейки и Циркуля; How to split a circle into three partsСкачать

Деление окружности на 3 и 6 равных частей (кратные 3 трём)

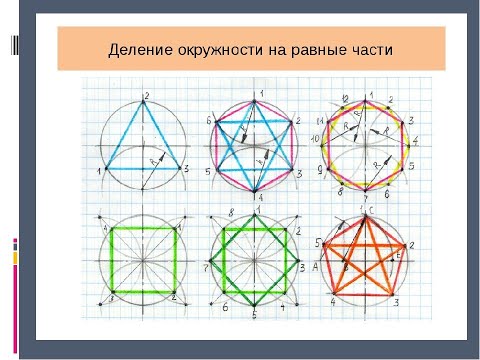
Для деления окружности на 3, 6 и кратное им количество частей, проводим окружность заданного радиуса и соответствующие оси. Деление можно начинать от точки пересечения горизонтальной или вертикальной оси с окружностью. Заданный радиус окружности последовательно откладывается 6-ть раз. Затем полученные точки на окружности последовательно соединяются прямыми линиями и образуют правильный вписанный шести-угольник. Соединение точек через одну даёт равносторонний треугольник, и деление окружности на три равные части.

Видео:Как разделить окружность на 3 равные части How to divide a circle into 3 equal partsСкачать

Деление окружности на 5 и 10 равных частей

Построение правильного пятиугольника выполняется следующим образом. Проводим две взаимно перпендикулярные оси окружности равные диаметру окружности. Делим правую половину горизонтального диаметра пополам с помощью дуги R1. Из полученной точки «а» в середине этого отрезка радиусом R2 проводим дугу окружности до пересечения с горизонтальным диаметром в точке «b». Радиусом R3 из точки «1» проводят дугу окружности до пересечения с заданной окружностью (т.5) и получают сторону правильного пятиугольника. Расстояние «b-О» даёт сторону правильного десятиугольника.

Деление окружности на N-ное количество одинаковых частей (построение правильного многоугольника с N сторон)

Выполняется следующим образом. Проводим горизонтальную и вертикальную взаимно перпендикулярные оси окружности. Из верхней точки «1» окружности проводим под произвольным углом к вертикальной оси прямую линию. На ней откладываем равные отрезки произвольной длины, число которых равно числу частей на которое мы делим данную окружность, например 9. Конец последнего отрезка соединяем с нижней точкой вертикального диаметра. Проводим линии, параллельные полученной, из концов отложенных отрезков до пересечения с вертикальным диаметром, разделив таким образом вертикальный диаметр данной окружности на заданное количество частей. Радиусом равным диаметру окружности, из нижней точки вертикальной оси проводим дугу MN до пересечения с продолжением горизонтальной оси окружности. Из точек M и N проводим лучи через чётные ( или нечётные) точки деления вертикального диаметра до пересечения с окружностью. Полученные отрезки окружности будут являться искомыми, т.к. точки 1, 2, …. 9 делят окружность на 9-ть ( N ) равных частей.

Видео:Деление окружности на равные части с помощью циркуляСкачать

Нахождение центра дуги окружности

Для нахождения центра дуги окружности нужно выполнить следующие построения: на данной дуге отмечаем четыре произвольные точки А, В, С, D и соединяем их попарно хордами АВ и СD. Каждую из хорд при помощи циркуля делим пополам, получив, таким образом, перпендикуляр, проходящий через середину соответствующей хорды. Взаимное пересечение этих перпендикуляров даёт центр данной дуги и соответствующей ей окружности.

Видео:Деление окружности на 3 равные частиСкачать

Покажите приемы деления окружностей на 3,6,12 частей с помощью циркуля, линейки и угольника

Деление окружности на 3 равные части.

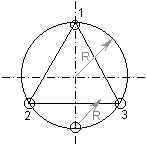
Чтобы разделить окружность радиуса R на 3 равные части и вписать в нее равносторонний треугольник, из точки пересечения диаметра с окружностью (например из точки А) описывают как из центра дополнительную дугу радиусом R. Получают точки 2 и 3. Точки 1, 2, 3 делят окружность на три равные части. Соединив прямыми линиями точки 1, 2, 3 строят вписанный равносторонний треугольник.

Деление окружности на 6 равных частей.

Чтобы разделить окружность на 6 равных частей, из двух противоположных точек (1 и 4) пересечения диаметра с окружностью описывают две дуги радиусом R. Получают точки (2, 3, 5, 6). Вместе с точками которые получились при пересечении диаметра с окружностью он делят окружность на 6 равных частей.

Деление окружности на 12 равных частей.

Для деления окружности на 12 равных частей из четырех точек пересечения осей симметрии с окружностью описывают 4 дуги радиусом R. Полученные точки, вместе с теми, которые получились при пересечении осей симметрии с окружностью, делят окружность на 12 равных частей.

Виды обозначений сечений на чертежах

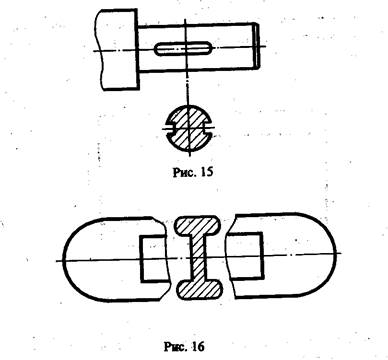
Чтобы показать поперечную форму деталей, пользуются изображениями, называемыми сечениями (рис. 13). Для того, чтобы получить сечение, деталь мысленно рассекают воображаемой секущей плоскостью в том месте, где нужно выявить её форму. Фигура, полученная в результате рассечения детали секущей плоскостью, изображается на чертеже. Следовательно сечением называется изображение фигуры, получающейся при мысленном рассечении предмета плоскостью или несколькими плоскостями.

На сечении показывается только то, что получается непосредственно в секущей плоскости.

Для ясности чертежа сечения выделяют штриховкой. Наклонные параллельные линии штриховки проводят под углом 45° к линиям рамки чертежа, а если они совпадают по направлению с линиями контура или осевыми линиями, то под углом 30° или 60°.

Вынесенное сечение.

Контур вынесенного сечения обводят сплошной толстой линией такой же толщины, как и линия, принятая для видимого контура изображения. Если сечение вынесенное, то, как правило проводят разомкнутую линию, два утолщенных штриха, и стрелки, указывающие направление взгляда. С внешней стороны стрелок наносят одинаковые прописные буквы. Над сечением пишут те же буквы через тире с тонкой чертой внизу. Если сечение представляет собой симметричную фигуру и расположено на продолжении линии сечения (штрихпунктирная), то обозначений не наносят.

Наложенное сечение.

Контур наложенного сечения – сплошная тонкая линия (S/2 – S/3), причем контур вида в месте расположения наложенного сечения не прерывают. Наложенное сечение обычно не обозначают. Но если сечение представляет собой не симметричную фигуру, проводят штрихи разомкнутой линии и стрелки, но буквы не наносят.

Обозначение сечений

Положение секущей плоскости указывают на чертеже линией сечения — разомкнутой линией, которая проводится в виде отдельных штрихов, не пересекающих контур соответствующего изображения. Толщина штрихов берётся в пределах от $ до 1 1/ ₂S, а длина их от 8 до 20 мм. На начальном и конечном штрихах перпендикулярно им, на расстоянии 2-3 мм от конца штриха, ставят стрелки, указывающие направление взгляда. У начала и конца линии сечения ставят одну и ту же прописную букву русского алфавита. Буквы наносят около стрелок, указывающих направление взгляда с внешней стороны, рис. 12. Над сечением делают надпись по типу А-А. Если сечение находится в разрыве между частями одного и того же вида, то при симметричной фигуре линию сечения не проврдяЯ4. Сечение можно располагать с поворотом, тогда к надписи А-А должен быть добавлен символ