Изобразите параллелепипед abcda1b1c1d1 и обозначьте векторы c1d1 ba1 ad

Видео:№84. Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение плоскостью, проходящейСкачать

Ваш ответ

Видео:№114. Изобразите параллелепипед ABCDA1B1C1D1 и отметьте на ребре АВ точку М. Постройте сечение паралСкачать

решение вопроса

Видео:№330. Нарисуйте параллелепипед ABCDA1B1C1D1 и обозначьте векторы C1D1, BA1Скачать

Похожие вопросы

• Все категории
• экономические 43,282
• гуманитарные 33,619
• юридические 17,900
• школьный раздел 606,989
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:№80. Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечения плоскостями АВС1Скачать

Изобразите параллелепипед abcda1b1c1d1 и обозначьте векторы c1d1 ba1 ad

Вопрос по геометрии:

1) упростите выражение B1D1+C1C+C1B+AC1+CA+A1D1

2) изобразите тетраэдр ABCD и вектор, равный BC+CD-BA

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

Этим вектором будет АД

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

Видео:№81. Изобразите параллелепипед ABCDA1B1C1D1 и отметьте точки М и N соответственноСкачать

Урок геометрии по теме «Перпендикулярность прямой и плоскости». 10-й класс

Разделы: Математика

Класс: 10

Цели:

1. закрепить вопросы теории по теме «Перпендикулярность прямой и плоскости»;
2. вырабатывать навыки применения теоретических знаний к решению типовых задач на перпендикулярность прямой и плоскости.

План:

1. Теоретический опрос.
   1. Доказательство изученных теорем у доски.
   2. Фронтальный опрос.
   3. Презентации учащихся по данной теме.
2. Решение задач.
   1. Решение устных задач по готовым чертежам.
   2. Решение письменных задач (по группам).
   3. Самостоятельная работа с индивидуальным заданием.
3. Итог урока. Задание на дом.

Ход урока

I. Теоретический опрос (4 ученика у доски)

1) доказать лемму о 2-ух параллельных прямых, одна из которых перпендикулярна к третьей;
2) доказать теорему о 2-ух параллельных прямых, одна из которых перпендикулярна к плоскости;
3) доказать обратную теорему о параллельности 2-ух прямых, перпендикулярных к плоскости;
4) доказать признак перпендикулярности прямой и плоскости.

Пока ученики готовятся у доски к ответу, с классом проводится фронтальный опрос.
(С помощью мультимедиапроектора на экране появляются вопросы (Приложение 1), и ученики отвечают на них)

1. Закончить предложение:

а) две прямые в пространстве называются перпендикулярными, если… (угол между ними равен 90°)
б) прямая называется перпендикулярной к плоскости, если… (она перпендикулярна к любой прямой, лежащей в этой плоскости)
в) если две прямые перпендикулярны к плоскости, то они… (параллельны)
г) если плоскость перпендикулярна к одной из двух параллельных прямых, то она… (перпендикулярна и к другой прямой)
д) если две плоскости перпендикулярны к одной прямой, то они… (параллельны)

2. Дан параллелепипед

б) Определите взаимное расположение:
1) прямой CC₁ и плоскости (DСВ) (ответ: они перпендикулярны)
2) прямой D₁C₁ и плоскости (DCB) (ответ: они параллельны)

Далее выслушиваются ответы учеников у доски с дополнениями и исправлениями по необходимости. Затем рассматриваются презентации по данной теме, подготовленные рядом учеников в качестве зачётных работ (Приложение 2, Приложение 3, Приложение 4).
(Накануне изучения каждой темы учащимся предлагается такой вариант зачёта)

II. Решение задач.

1. Решение задач по готовым чертежам (Устно)

№1

Дано: ∆ ABC — прямоугольный; AM ⊥ AC; M ∉ (ABC)
Доказать: AC ⊥ (AMB)
Доказательство: Т.к. AC ⊥ AB и AC ⊥ AM, а AM ⋂ AB, т.е. АМ и АВ лежат в плоскости (АМВ), то AC ⊥ (AMB) по признаку перпендикулярности прямой и плоскости.
Ч.т.д.

№2

Дано: ВМDC — прямоугольник, M ∉ (ABC), MB ⊥ AB
Доказать: CD ⊥ (ABC)
Доказательство: MB ⊥ BC, т.к. ВМDC – прямоугольник, MB ⊥ AB по условию, BC ⋂ AB, т.е. ВС и АВ лежат в плоскости (АВС) ⇒ MB ⊥ (ABC) по признаку перпендикулярности прямой и плоскости. СD ∥ МВ по свойству сторон прямоугольника ⇒ CD ⊥ (ABC) по теореме о двух параллельных прямых, одна из которых перпендикулярна к плоскости (то и другая прямая перпендикулярна к этой плоскости).
Ч.т.д.

№3

Дано: АВСD – прямоугольник, M ∉ (ABC), MB ⊥ BC
Доказать: AD ⊥ AM
Доказательство:
1) ∠ABC = 90°, т.к. АВСD – прямоугольник ⇒ BC ⊥ AB, BS ⊥ MB по условию, MB ⋂ AB = B, т.е. МВ и АВ лежат в плоскости (АМВ) ⇒ BC ⊥ (AMB) по признаку перпендикулярности прямой и плоскости.
2) BC ∥ AD (по свойству сторон прямоугольника) ⇒ AD ⊥ (AMB) по теореме о двух параллельных прямых, одна из которых перпендикулярна плоскости (то и другая прямая перпендикулярна к этой плоскости).
3) Т.к. AD ⊥ (AMB) ⇒ AD ⊥ AM по определению прямой, перпендикулярной плоскости.
Ч.т.д.

№4

Дано: АВСD – параллелограмм, M ∉ (ABC), МВ = МD, МА = МС
Доказать: MO ⊥ (ABC)
Доказательство:
1) Т.к. О – точка пересечения диагоналей параллелограмма, то АО = СО и ВО = DO. ∆ BMD — равнобедренный, т. к. ВМ = МD по условию, значит МО — медиана и высота, т.е. MO ⊥ BD.
2) Аналогично доказывается в ∆ AMC: MO ⊥ AC.
3) Итак, MO ⊥ BD и MO ⊥ AC. а ВD и АС – пересекающиеся прямые, лежащие в плоскости (АВС) ⇒ MO ⊥ (ABC) по признаку перпендикулярности прямой и плоскости.
Ч.т.д.

(Устные ответы к каждой задаче требуется обосновывать, проговаривая всякий раз формулировки применяемых теорем)

2. Решение письменных задач

Класс делится на три группы (например, по рядам), и каждой группе даётся задача с последующей проверкой решения у доски.

№1.2 (№125 учебника)

Через точки P и Q прямой РQ проведены прямые, перпендикулярные к плоскости α и пересекающие её соответственно в точках P₁ и Q₁. Найдите P₁Q₁, если PQ = 15 cм; PP₁ = 21,5 cм; QQ₁ = 33,5 cм.
Решение:

1) PP₁ ⊥ α и QQ₁ ⊥ α по условию ⇒ PP₁ ∥ QQ₁ (обосновать);
2) PP₁ и QQ₁ определяют некоторую плоскость β, α ⋂ β = P₁Q₁;
3) PP₁Q₁Q — трапеция с основаниями PP₁ и QQ₁, проведём PK ∥ P₁Q₁;
4) QK = 33,5 — 21,5 = 12 (см)

P1Q1 = PK =

= 9 см.

№2.2

1) ∆ ABD: ∠BAD = 90°; АD = BC = 8 см;

ВD =

см;

2) ∆ DD₁B: ∠D₁DB = 90°;

DD1 =

= 12 см;

3) SBB1D1D = BD ∙ DD1 =

см 2 .

Ответ:

см 2 .

№3.2

Отрезок МН пересекает плоскость α в точке К. Из концов отрезка проведены прямые МЕ и НР, перпендикулярные к плоскости α. НР = 4 см; МЕ = 12 см; НК = 5 см. Найдите отрезок РЕ.
Решение:

1) Т.к. прямые МЕ и НР перпендикулярны к плоскости α, то МЕ ∥ НР (обосновать) и через них проходит некоторая плоскость β. α ⋂ β = EP;
2)МЕ ⊥ EP; НР ⊥ EP(обосновать), т.е. ∠MEK = ∠HPK = 90°;

3) ∆ HPK: KP =

= 3 см;

4) ∠EMK = ∠PHK (накрест лежащие для параллельных прямых МЕ и НР и секущей МН),

тогда ∆ MEK ∆ HPK по двум углам и

; т.е.

⇒ EK =

= 9 см,

РЕ = РК + КЕ, РЕ = 3 + 9 = 12 см.

Ответ: РЕ = 12 см.

3. Самостоятельная работа (направлена на проверку усвоения материала по данной теме)

1) AA₁ ⊥ AB, AA₁ ⊥ AD, а AB ⋂ AD = A ⇒ AA₁ ⋂ (ABC) (по признаку перпендикулярности прямой и плоскости), а т.к. AA₁ ∥ BB₁, то BB₁ ⊥ (ABC) ⇒ BB₁ ⊥ BD;
2) ∆ ABD: ∠BAD = 90°. По теореме Пифагора:

BD =

= 20 см;

3) ∆ B₁BD – прямоугольный. По теореме Пифагора:

B1B =

= 15 см.

1) BB₁ ⊥ AB, BB₁ ⊥ BC, а AB ⋂ BC = B ⇒ BB₁ ⋂ (ABC) (по признаку перпендикулярности прямой и плоскости), а т.к. BB₁ ∥ AA₁, то AA₁ ⊥ (ABC) ⇒ AA₁ ⊥ AC;
2) Используя свойство диагоналей ромба, имеем в ∆ AOB: ∠AOB = 90°, BO = ½ BD = 8 см. По теореме Пифагора:

AO =

= 6 см,

AO = ½ AC ⇒ AC = 12 см;
3) ∆ A₁AC – прямоугольный. По теореме Пифагора:

AA1 =

= 5 см.

Индивидуальное задание для более сильных учеников. (Вариант III)

1) Т.к. CD ⊥ (FDC) ⇒ CD ⊥ AC и CD ⊥ BC, т.е. ∆ ADC, ∆ BDC – прямоугольные;
2) ∆ ADC = ∆ BDC (по двум катетам) ⇒ AD = BD, т.е. ∆ ADB – равнобедренный и DM – медиана, а значит и высота; 3) DC ⊥ MC ⇒ MCD – прямоугольный,

тогда MC =

= 9;

4) ∆ ABC – равносторонний, поэтому СМ – медиана и высота, т.е. ∆ MCB – прямоугольный, ∠B = 60°,

sin ∠B =

, тогда

,

а АВ = ВС (по условию).
5) S_{∆ ADB} = ½ DM ∙ AB;

S∆ ADB = ½ ∙ 15 ∙

.

Ответ:

III. Подводятся итоги урока. Задание на дом: повторить теоретический материал по изученной теме, глава II, №130, №131.

Для подготовки к уроку использовались материалы учебника «Геометрия – 10-11» авторов Л.С. Атанасяна, В.Ф. Бутузова и др., методические рекомендации к учебнику «Изучение геометрии в 10-11 классах» авторов С.М. Саакяна, В.Ф. Бутузова, «Поурочные разработки по геометрии» автора В.А. Яровенко.

🎬 Видео

№82. Изобразите параллелепипед ABCDA1B1C1D1 и отметьте внутреннюю точку М грани АА1В1ВСкачать

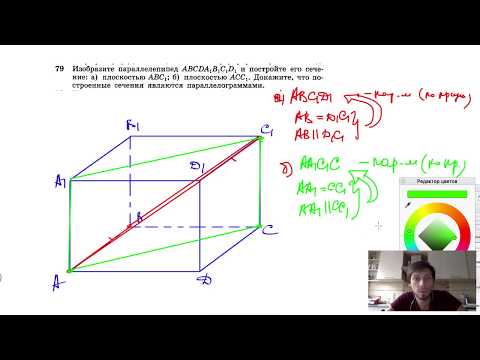
№79. Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение: а) плоскостью АВС1;Скачать

№83. Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение плоскостью, проходящей черезСкачать

№86. Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение плоскостью, проходящейСкачать

№359. Дан параллелепипед ABCDA1B1C1D1. а) Разложите вектор BD1 по векторам ВА, ВС и ВВ1.Скачать

№358. Дан параллелепипед ABCDA1B1C1D1. Назовите вектор, начало и конец которого являются вершинамиСкачать

№85. Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение плоскостью BKL, где КСкачать

№87. Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение плоскостью MNK, где точки М,Скачать

№78. На рисунке 42 изображен параллелепипед ABCDA1B1C1D1, на ребрах которого отмечены точки МСкачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

№76. Дан параллелепипед ABCDA1B1C1D1. Докажите, что AC||A1C1 и BD||B1D1.Скачать

№339. Дан параллелепипед ABCDAСкачать

№327. На рисунке 97 изображен параллелепипед ABCDA1B1C1D1. Назовите вектор, нСкачать

№355. Дан параллелепипед ABCDA1B1C1D1. Какие из следующих трех векторов компланарныСкачать

10 класс, 44 урок, Правило параллелепипедаСкачать