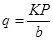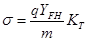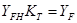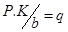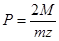Диаметр окружности вершин зубьев цилиндрического зубчатого колеса определяется по формуле

Видео:Модуль шестерни и параметры зубчатого колесаСкачать

Зацепления зубчатые относятся к передачам (подвиж­ным соединениям) и передают движение от двигателя к ис­полнитель­ным механизмам. К составным частям зубчатых передач отно­сятся зубчатые колеса (цилиндрические, кони­ческие), червяки, рейки.

Диаметр делительной ок­ружности d является од­ним из основных параметров, по кото­рому произ­водят расчет зубча­того ко­леса:

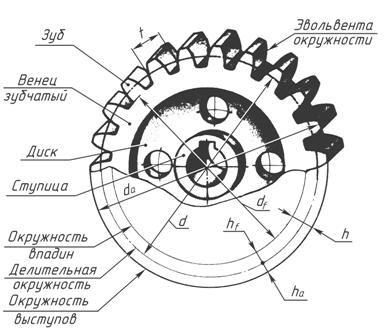
где z – число зубьев;

Модуль зацепления m – это часть диаметра делительной ок­ружности, приходящейся на один зуб:

где t – шаг зацепления.

где h _a – высота головки зуба, h _a = m ; h _f – высота ножки зуба, h _f = 1,25 m .

Диаметр окружности выступов зубьев :

Диаметр окружности впадин :

Служит для передачи вращения при параллельных осях валов.

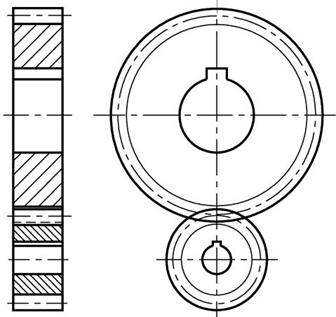
ГОСТ 9563-60 предусматривает два ряда модулей m = 0,05…100 мм.

Ряд 1: … 0,5; 0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16 …

Ряд 2: … 0,55; 0,7; 0,9; 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14 …

Примечание. Ряд 1 следует предпочитать ряду 2 .

Служит для преобразования вращательного движения в возвратно-посту­пательное.

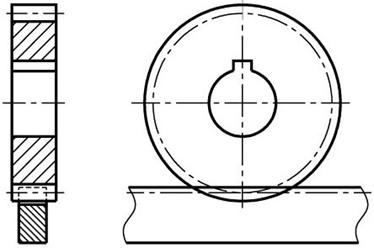
ГОСТ 9563-60 предусматривает два ряда модулей m = 0,05…100 мм.

Ряд 1: … 0,5; 0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16 …

Ряд 2: … 0,55; 0,7; 0,9; 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14 …

Примечание. Ряд 1 следует предпочитать ряду 2.

Служит для передачи вращательного движения между валами со скрещивающимися осями.

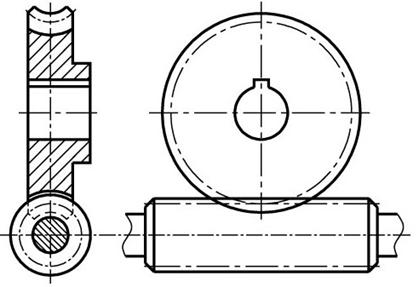
ГОСТ 19672-74 устанавливает два ряда значений модулей m (мм).

Ряд 1: … 1; 1,25; 1,6; 2; 2,5; 3,15; 4; 5; 6,3; 8; 10 …

Ряд 2: … 1,5; 3; 3,5; 6; 7 …

Примечание. Ряд 1 следует предпочитать ряду 2.

Служит для передачи вращения при пересекающихся осях валов.

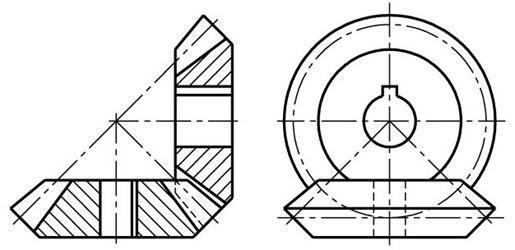
ГОСТ 9563-60 предусматривает два ряда модулей m  = 0,05…100 мм.

Ряд 1: … 0,5; 0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16 …

Ряд 2: … 0,55; 0,7; 0,9; 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14 …

Примечание. Ряд 1 следует предпочитать ряду 2.

Видео:6.3 Зубчатые цилиндрические передачиСкачать

Расчет основных геометрических параметров цилиндрических прямозубых колес

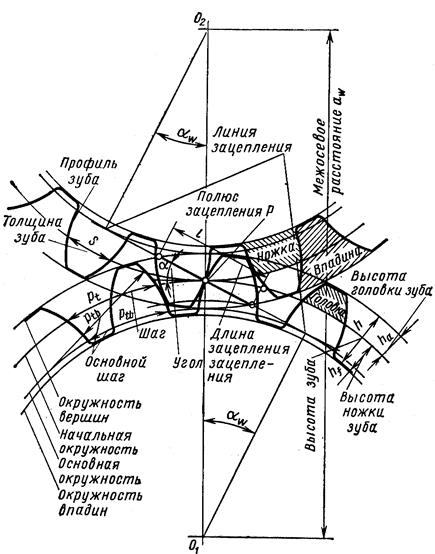
Эвольвентное зацепление двух зубчатых колес характеризуется следующим параметрами (ГОСТ 16530-70) (рис. 13.3).

Начальные окружности (d_w1 и d_w2) – воображаемые окружности, которые в процессе работы передачи перекатываются одна по другой без скольжения. Начальные окружности появляются у зубчатых колес в собранной передаче. Для отдельно взятого колеса понятие начальной окружности отсутствует. Оно имеет делительную окружность.

Окружность вершин зубьев (d_α) – окружность ограничивающая головки зубьев.

Окружность впадин (d_f) – окружность, проходящая через основания впадин зубьев.

Основная окружность (d_b1 и d_b2) – окружность, при развертке которой получается эвольвента.

Делительная окружность (d₁ и d₂) – окружность зубчатого колеса, по которой обкатывается делительная окружность (прямая) инструмента в процессе нарезания зубьев. Делительная окружность колеса является начальной только в процессе изготовления (нарезания) зубьев. У некорригированных колес и при высотной коррекции начальные и делительные окружности совпадают.

Полюс зацепления (точка “P”) – точка касания начальных окружностей.

Рис. 13.3. Элементы зубчатого зацепления

Окружной шаг зацепления (P_t) – расстояние между одноименными профилями, измеренное по дуге делительной окружности, зубчатого колеса.

Головка зуба (h_α) – часть зуба между делительной окружностью зубчатого колеса и его окружностью вершин зубьев.

Ножка зуба (h_f) – часть зуба между делительной окружностью и его окружностью впадин.

Высота зуба (h) равна сумме высот головки и ножки зуба.

Дуга зацепления (l) – путь по начальной окружности, проходимой точкой профиля за время зацепления пары сопряженных зубьев.

Коэффициент перекрытия (ε) – отношение дуги зацепления к окружному шагу.

Линия зацепления (N₁ и N₂) – линия, по которой перемещается точка касания зубьев. Линия зацепления проходит через полюс зацепления и является касательной к основным окружностям.

Угол зацепления (α_w) – угол между линией зацепления и касательной к начальным окружностям в полюсе зацепления.

Модуль зацепления (m). Все модули стандартизованы в пределах от 0,05 мм до 100 мм.

Рассмотренные параметры составляют определенные кинематические зависимости. В табл. 10 приводятся основные соотношения для цилиндрических некорригированных зубчатых передач внешнего зацепления.

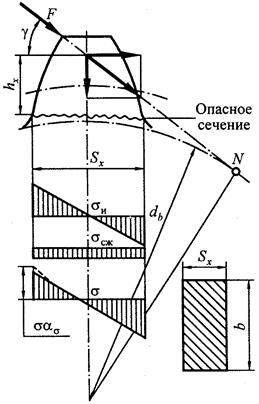
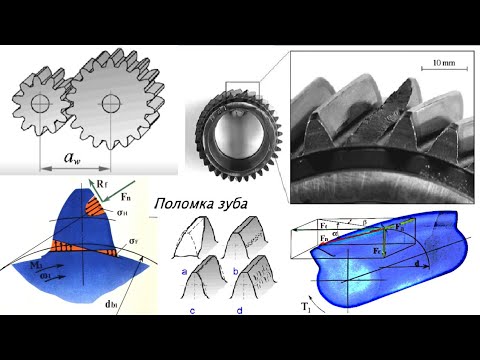
В расчётах зуб зубчатого колеса рассматривают как балку, защемленную одним концом и нагруженную силой (Q_n). Такое положение нагрузки принимается как наиболее опасное.

Наиболее опасное сечение, где наиболее вероятен излом зуба, находится у его корня в зоне наибольшей концентрации напряжений. Максимальное напряжение возникает на стороне сжатия (нерабочая сторона). Однако следует отметить то, что расчет на прочность необходимо производить по напряжению на рабочей стороне, т.к. на этой растянутой стороне зуба здесь может образоваться усталостная трещина.

Основные соотношения для цилиндрических
некорригированных зубчатых передач внешнего зацепления

Параметры зацепления	Формулы
Окружной модуль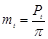
Нормальный модуль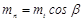
Нормальный шаг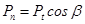
Межосевое расстояние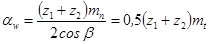
Высота головки зуба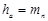
Высота ножки зуба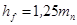
Высота зуба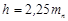
Радиальный зазор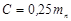
Делительный диаметр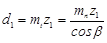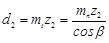
Начальный диаметр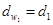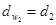
Диаметр основной окружности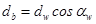
Диаметр вершин зубьев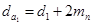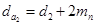
Диаметр впадин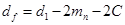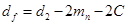
Коэффициент перекрытия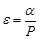

13.3. Расчет зубьев
цилиндрических прямозубых зубчатых колес на изгиб

— для обозначения расчета на изгиб, который проводится по ножке зуба принят индекс F (от термина ножка – Fut – на английском и немецком языках).

— для обозначений расчета на контактную прочность принят индекс H, в честь автора теории расчетов контактных напряжений Г. Герца.

Расчет ведется по расчетной окружной силе (q), отнесенной к единице ширины венца.

где: P – передаваемое окружное усилие;

b – ширина венца зубчатого колеса (длина зуба);

K – коэффициент нагрузки, учитывающий дополнительные вредные явления (удары).

q – расчетная окружная сила, отнесенная к единице ширины венца (b).

Нормальная удельная сила равна:

Перенесем силу давления q_n вдоль линии ее действия (линия зацепления) в точку, расположенную на оси симметрии зуба (рис. 13.4) и разложим на две составляющие: изгибающую зуб (q_ncosα_n), вызывающую в опасном сечении напряжения изгиба (σ_u) и сжимающую зуб (q_nsinα), вызывающую в зубе напряжения сжатия (σ_cж). Угол «γ» несколько больше угла профиля «α_w» (γ = α_w = 20˚).

Номинальное напряжение в опасном сечении:

;
;

;
;

;
;
.

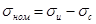
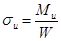
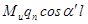
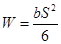
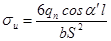
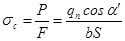
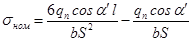
Рис. 13.4. Схема расчета зубьев на изгиб

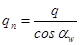
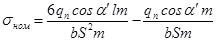
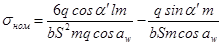
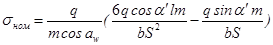
Умножим числитель и знаменатель на модуль «m» и заменим получим:

,

,

;

приняв: ;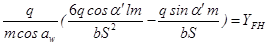

получим: .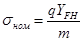

;

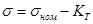
обозначив:

получим: ,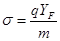

где: K_T – теоретический коэффициент концентрации напряжений;

Y_FHU, Y_F – коэффициенты прочности зубьев соответственно по номинальным и местным напряжениям;

Y_FH – представляет собой номинальное напряжение в опасном сечении зуба при m = 1 и q = 1, а Y_F – местное напряжение при тех же условиях.

Технические расчеты удобно вести по формулам, в которых условия нагружения заданы в форме номинальных крутящих моментов М (ктс.см) или мощности (кВт), частоты вращения n (об/мин) и коэффициента нагрузки К.

;

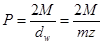
Для технических проверочных расчетов следует умножить P.K и приняв

получим: ;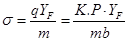

если

то: .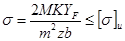

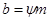
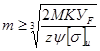
Модуль и ширина зубчатого венца, прежде всего, определяют прочность зуба на изгиб. Приняв и решив последнее уравне­ние относительно модуля, после преобразований получим:

.

Наиболее рациональной формой расчет, обеспечивающей равнопрочностъ зубьев по выкрашиванию и излому, является определение модуля по известному межосевому расстоянию “a_w” и ширине зубчатого венца “b” полученным из расчета на конкретную прочность.

.

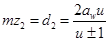
После преобразования получим:

,

.

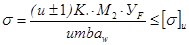
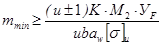
Для большинства редукторов общего назначения:

;

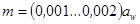
коэффициент нагрузки К можно выразить:

,

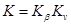
здесь: K_β – коэффициент концентрации нагрузки;

K_v – коэффициент динамичности нагрузки.

Видео:Что такое МОДУЛЬ шестерни? Ты ТОЧНО поймешь!Скачать

Модуль шестерни: виды, определение, стандартные показатели

Видео:Как определить шестернюСкачать

Что представляет собой шестерня

Шестерня – это небольшое колесико с зубьями, которое крепится к специальной вращающейся оси. Поверхность у шестеренки в данном случае может быть как конической, так и цилиндрической.

Шестеренчатые передачи также имеют свою классификацию:

1. Прямозубые. Наиболее распространенный вид шестеренок, у которых зубья зачастую располагаются в радиальных плоскостях.
2. Скошенные. По-другому этот тип называется еще косозубым, а его использование в ходу у бензо- и электрических инструментов. По отношению к вращающейся оси они находятся под определенным углом.
3. Червячные. Их еще называют спиральными шестернями, которые используются преимущественно для рулевого управления автомобилем.
4. Винтовые. Они имеют зачастую форму цилиндра, а также расположены по всей линии винта. Располагаются такие шестеренки на валах, которые расположены перпендикулярно к вращающейся оси.

Данные разновидности являются наиболее распространенными, однако далеко не единственными, поэтому используемый вид напрямую соотносится с тем, какую функцию он должен будет выполнять.

При этом каждая шестеренка имеет определенное количество зубьев, что определяется ее назначением. Разница между количеством используемых зубьев необходима, поскольку благодаря этому фактору появляется возможность регулировать обороты вала и крутящийся момент. Шестеренки также разделяются на ведущие и ведомые. Ведущей называется та шестерня, к которой вращательный момент подводится снаружи, а ведомой – та, с которой она снимается.

Почему шестеренку называют так?

Технически это понятно. Изначально «шестерёнка» — самое маленькое колесо в зубчатой передаче. Меньше шести зубьев там не бывает даже в теории, захват не обепечивается. … В машиностроении ведомое колесо зубчатой передачи редуктора называется колесом».

Видео:Лекция 4. Конические зубчатые передачиСкачать

Характеристики и применение

Зубья шестеренки находятся в радиальных плоскостях. Линия контакта прямозубых цилиндрических шестерней параллельна оси вращения.

В зависимости от необходимых нагрузочных характеристик и точности передаваемого вращения, подбирается модуль (расстояние между центрами зубов) от 1 до 6.

Используется в подвижных частях механизмов соместно с зубчатой рейкой.

Цилиндрическая зубчатая передача применяется во всех типах автоматических ворот, конвейерных линиях с повышенной нагрузкой, 3D принтерах, станках ЧПУ и многом другом.

Параметры модуля шестерни

Рассматриваемая характеристика обозначается литерой m, указывает на прочность зубчатых передач. Единица измеряется в миллиметрах (чем выше нагрузка на передачу, тем больше модульное значение). В расчете параметра используются следующие показатели:

• диаметр делительной окружности;
• шаг и число зубьев;
• эвольвент (диаметр основной окружности);
• аналогичная характеристика впадин темной шестеренки;
• высота зуба темного и светлого колеса.

В машиностроительной отрасли расчеты ведутся по стандартным значениям для удобства изготовления и замены шестерен с числами от 1-го до 50-ти.

Что такое модуль на чертеже?

Модуль — это унифицированный элемент любых систем, состоящий из взаимозаменяемого комплекса деталей массового производства. Чертеж модуля выполняется на основании ГОСТ 2.109-73 — единая система конструкторской документации (ЕСКД).

Видео:Геометрический расчет по диаметрам вершин зубьев. Валы и механические передачи 3DСкачать

Как найти модуль шестерни?

Как определить модуль косозубой шестерни.

1. Измеряем диаметр:
2. Диаметр окружности выступов (De) равен 28,6 мм.
3. Считаем количество зубьев. Z=25.
4. Делительный диаметр (De) делим на количество зубьев 25 +2. Равно 28,6 разделить на 27=1,05925925925926.
5. Округляем до ближнего модуля. Получается модуль 1.

Видео:Зубчатые передачиСкачать

Как узнать высоту зуба шестерни?

h = ha + hf, где ha – высота головки зуба, ha = m; hf – высота ножки зуба, hf = 1,25m.

Видео:4 5 расчет зубчатого колесаСкачать

Как найти делительный диаметр шестерни?

Диаметр делительной окружности d является одним из основных параметров, по которому производят расчет зубчатого колеса: d = m × z, где z – число зубьев; m – модуль.

Как обозначается делительный диаметр?

Окружность, являющаяся начальной при зацеплении с рейкой – делительная; её диаметр обозначается d (рис. 2). Для колес без смещения делительные окружности совпадают с начальными. Толщина зуба по делительной окружности S равна ширине впадины между двумя зубьями е.

Видео:Лекция 6 Взаимозаменяемость зубчатых колесСкачать

Формула расчета параметров прямозубой передачи

Чтобы определить параметры прямозубой шестеренки, потребуется выполнить некоторые предварительные вычисления. Длина начальной окружности равна π×D, где D — ее диаметр.

Расчет модуля зубчатого колеса

Шаг зацепления t – это расстояние между смежными зубами, измеренное по начальной окружности. Если это расстояние умножить на число зубов z, то мы должны получить ее длину:

проведя преобразование, получим:

Если разделить шаг на число пи, мы получим коэффициент, постоянный для данной детали зубчатой передачи. Он и называется модулем зацепления m.

размерность модуля шестерни — миллиметры. Если подставить его в предыдущее выражение, то получится:

выполнив преобразование, находим:

Отсюда вытекает физический смысл модуля зацепления: он представляет собой длину дуги начальной окружности, соответствующей одному зубцу колеса. Диаметр окружности выступов De получается равным

где h’- высота головки.

Высоту головки приравнивают к m:

Проведя математические преобразования с подстановкой, получим:

Диаметр окружности впадин Di соответствует De за вычетом двух высот основания зубца:

где h“- высота ножки зубца.

Для колес цилиндрического типа h“ приравнивают к значению в 1,25m:

Устройство зубчатого колеса

Выполнив подстановку в правой части равенства, имеем:

что соответствует формуле:

и если выполнить подстановку, то получим:

Иначе говоря, головка и ножка зубца относятся друг к другу по высоте как 1:1,25.

Следующий важный размер, толщину зубца s принимают приблизительно равной:

• для отлитых зубцов: 1,53m:
• для выполненных путем фрезерования-1,57m, или 0,5×t

Поскольку шаг t приравнивается к суммарной толщине зубца s и впадины sв, получаем формулы для ширины впадины

• для отлитых зубцов: sв=πm-1,53m=1,61m:
• для выполненных путем фрезерования- sв= πm-1,57m = 1,57m

Характеристики конструкции оставшейся части зубчатой детали определяются следующими факторами:

• усилия, прикладываемые к детали при эксплуатации;
• конфигурация деталей, взаимодействующих с ней.

Детальные методики исчисления этих параметров приводятся в таких ВУЗовских курсах, как «Детали машин» и других. Модуль шестерни широко используется и в них как один из основных параметров.

Для отображения шестеренок методами инженерной графики используются упрощенные формулы. В инженерных справочниках и государственных стандартов можно найти значения характеристик, рассчитанные для типовых размеров зубчатых колес.

Видео:Детали машин. Лекция 2.3. Основы расчета зубчатых передачСкачать

Что такое модуль зубчатого колеса?

m — модуль колеса. Модулем зацепления называется линейная величина в π раз меньшая окружного шага P или отношение шага по любой концентрической окружности зубчатого колеса к π, то есть модуль — число миллиметров диаметра делительной окружности приходящееся на один зуб.

Видео:SolidWorks. Создание параметрического зубчатого колесаСкачать

Чему равен модуль нормального зубчатого колеса?

Модуль зубчатого колеса, геометрический параметр зубчатых колёс. Для прямозубых цилиндрических зубчатых колёс модуль m равен отношению диаметра делительной окружности dд к числу зубьев z или отношению шага t по делительной окружности к числу: m = dд/z = ts/p.

Видео:Лекция 5. Червячные передачиСкачать

Какие бывают зубчатые колеса?

Виды зубчатых колес, шестерен

• Поперечный профиль зуба Обычно шестерни имеют профиль зубьев с эвольвентной боковой формой. …
• Продольная линия зуба Прямозубые шестерни …
• Шестерни с внутренним зацеплением …
• Винтовые шестерни …
• Секторные шестерни …
• Шестерни с круговыми зубьями

Прямозубые и косозубые колесики

Модуль и диаметр шестерни прямозубого типа — один из самых востребованных видов. Зубцы размещаются в радиальных плоскостях, а площадь контакта пары колес параллельна оси вращения. Аналогичным образом располагаются оси обеих шестерен.

Косозубые колесики представляют собой усовершенствованную вариацию вышеуказанной модификации. Зубцы находятся под определенным углом к вращательной оси. Зацепление осуществляется плавней и тише, что позволяет эксплуатировать элементы в малошумных приспособлениях, гарантируя передачу большего крутящего момента на высокой скорости. К минусам относят увеличенную площадь контакта зубцов, провоцирующую повышенное трение и нагрев деталей. Это чревато ослаблением мощности и повышенным расходом смазки. Кроме того, механическое воздействие вдоль оси шестерни требует использования упорных подшипников для монтажа вала.

Шевронные модификации и аналоги с внутренним зацеплением

Шевронные шестерни позволяют справиться с проблемами механической осевой силы. В отличие от прямых и косозубых версий, зубья выполнены в виде литеры V. Осевое воздействие двух половин приспособления компенсируется взаимодействием, что дает возможность избежать применения упорных подшипников на валу. Указанная модель самостоятельно устанавливается по оси, один из рабочих редукторов монтируется на цилиндрических укороченных подшипниках (плавающие опоры).

Модуль шестерни с внутренним зацеплением оснащается зубцами, имеющими нарезку внутри. Эксплуатация детали предполагает односторонние обороты ведущего и ведомого колеса. В такой конструкции меньше затрат уходит на трение, что способствует повышению КПД. Подобные приспособления применяются в механизмах, ограниченных по габаритным размерам, а также планетарных передачах, специальных насосах и танковых башенках.

Винтовые, круговые, секторные версии

Модуль шестерни винтового типа представляет собой цилиндр с зубцами, которые размещены по винтовому направлению. Подобные элементы устанавливаются на непересекающиеся валы, расположенные перпендикулярно по отношению друг к другу. Угол совмещения составляет 90 градусов.

Секторное зубчатое колесо — часть любой шестерни, применяемая в передачах, где не нужно вращение основного элемента на полный оборот. Такая деталь дает возможность сэкономить ценное пространство в размерах полноценного аналога.

Шестерни по модулю и количеству зубьев с круговым расположением отличаются контактным соприкосновением в одной точке зацепления, расположенной параллельно основным осям. Второе название механизма — передача Новикова. Она обеспечивает хорошие ходовые характеристики, плавную и бесшумную работу, повышенную зацепляющую способность. При этом коэффициент полезного действия таких деталей немного ниже аналогов, а процесс изготовления существенно сложнее. Указанные детали имеют значительно ограниченную отрасль эксплуатации ввиду своих особенностей.

Конические шестерни

Конические шестерни имеют различные виды, отличаются они по форме линий зубьев, с прямыми, с криволинейными, с тангенциальными, с круговыми зубьями. Применяются конические зубчатые передачи в машинах для движения механизма, где требуется передать вращение с одного вала на другой, оси которых пересекаются. Например, в автомобильных дифференциалах, для передачи момента от двигателя к колесам.

Зубчатая рейка

Зубчатая рейка является частью зубчатого колеса с бесконечным радиусом делительной окружности. Вследствие этого ее окружности представляют собой прямые параллельные линии. Эвольвентный профиль зубчатой рейки тоже имеет прямолинейное очертание. Это свойство эвольвенты является наиболее важным при изготовлении зубчатых колёс. Передачу с применением зубчатой планки (рейки) называют — реечная передача (кремальера), она используется для преобразования вращательного движения в поступательное и наоборот. Состоит передача из зубчатой рейки и прямозубого зубчатого колеса (шестеренки). Применяется такая передача в зубчатой железной дороге.

Звездочка

Шестерня-звезда — это основная деталь цепной передачи, которая используется совместно с гибким элементом — цепью для передачи механической энергии.

Коронная шестерня

Коронная шестерня – это особый тип шестерен, их зубья находятся на боковой поверхности. Такая шестерня работает, как правило, в паре с прямозубой или с барабаном (цевочное колесо), состоящим из стержней. Такая передача используется в башенных часах.

Видео:6.4 Зубчатые конические передачиСкачать

В чем заключаются сходства между шестерней и зубчатым колесом

Между шестерней и зубчатым колесом можно отметить несколько схожих моментов:

• Как и шестерня, зубчатое колесо может быть как ведомым, так и ведущим элементом в общей системе.
• У шестерни и у зубчатого колеса форма может быть как цилиндрической, так и конической, все зависит от той функции, которую конкретная деталь выполняет.
• При помощи шестеренки и зубчатого колеса можно маневрировать на почве скорости вращательного элемента, либо уменьшая ее, либо увеличивая.
• Шестеренки и зубчатые колеса одинаково эффективно можно использовать на электрических и бензоинструментах, однако больше всего используют именно шестеренки, так как они обеспечивают устойчивость механизма.
• Шестеренка и зубчатое колесо могут использоваться для запуска вращательных осей.

Внешние сходства между шестеренкой и зубчатым колесом обоснованы также еще тем, что зачастую эти два элемента могут выполнять схожие функции и быть взаимозаменяемыми в определенных системах и механизмах.

Видео:Зубонарезание для чайников за 6 минут. Часть I - теорияСкачать

Когда применяют цилиндрические зубчатые передачи?

Цилиндрической зубчатой передачей называется передача с параллельными осями. Косозубые передачи применяют при окружных скоростях м/с; шевронные передачи – преимущественно в тяжело нагруженных передачах. … Кинематика и геометрия цилиндрические зубчатых колес.

Видео:Лекция 3.2 Расчет цилиндрических зубчатых передачСкачать

Подытожим

Расчетные чертежи и схемы для шестеренок различных конфигураций преимущественно совпадают для косых и прямозубчатых версий. Основные различия возникают при расчетах на прочность. В графических отображениях применяются характеристики, ориентированные на типовые габаритные размеры шестеренок. Среди представленного ассортимента на рынке вполне реально подобрать зубчатое колесо с необходимыми характеристиками и прочностными показателями.

🌟 Видео

КПД эвольвентного прямозубого зацепления. (Excel-калькулятор).Скачать

7.1 Червячные передачиСкачать

Шестеренки. Расчет и изготовление в домашней мастерской.Скачать

Лекция «Червячные передачи»Скачать

Лекция «Конические зубчатые передачи»Скачать