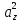Использование элементов алгебры матриц является одним из основных методов решения многих экономических задач. Особенно этот вопрос стал актуальным при разработке и использовании баз данных: при работе с ними почти вся информация хранится и обрабатывается в матричной форме.
Рассмотрим типичные задачи, использующие понятие вектора и его свойства.
1. Предприятие выпускает ежесуточно четыре вида изделий, основные производственно-экономические показатели которых приведены в табл. 16.1.
Требуется определить следующие ежесуточные показатели: расход сырья S, затраты рабочего времени Т и стоимость Р Выпускаемой продуции предприятия.
Решение. По данным табл. 16.1 составим четыре вектора, характеризующие весь производственный цикл:




Тогда искомые величины будут представлять собой соответствующие скалярные произведения вектора ассортимента 
2. Предприятие выпускает 4 вида изделий с использованием 4-х видов сырья. Нормы расхода сырья даны как элементы матрицы А:
Требуется найти затраты сырья на каждый вид изделия при заданном плане их выпуска: соответственно 60, 50, 35 и 40 ед.
Решение. Составим вектор-план выпуска продукции
Тогда решение задачи дается вектором затрат, координаты которого и являются величинами затрат сырья по каждому его виду; этот вектор затрат вычисляется как произведение вектора 
3. Пусть затраты 4-х видов сырья на выпуск 4-х видов продукции характеризуются матрицей А, приведенной в предыдущей задаче. Требуется найти: а) общие затраты на сырье для каждого вида продукции и его перевозку; б) общие затраты на сырье и его транспортировку при условии заданного вектора-плана предыдущей задачи, если известны себестоимости каждого вида сырья и его доставки (соответственно 4, 6, 5, 8 и 2, 1, 3, 2 ден. ед.).
Решение. Составим матрицу себестоимостей сырья и его доставки (соответственно 1-я и 2-я строки):
Тогда ответ на первый вопрос задачи дается в виде произведения матрицы А на транспонированную матрицу CT:
Суммарные затраты на сырье и его доставку (в денежных единицах) при векторе-плане выпуска продукции 

4. В табл. 16.2 приведены данные о дневной производительности 5 предприятий, выпускающих 4 вида продукции с потреблением 3-х видов сырья, а также продолжительность работы каждого предприятия в году и цена каждого вида сырья.
1) годовую производительность каждого предприятия по каждому виду изделий;
2) годовую потребность каждого предприятия по каждому виду сырья;
3) годовую сумму кредитования каждого предприятия для закупки сырья, необходимого для выпуска продукции указанных видов и количеств.
Решение. Нужно составить матрицы, характеризующие весь интересующий нас экономический спектр производства, а затем при помощи соответствующих операций над ними получить решение данной задачи. Прежде всего приведем матрицу производительности предприятий по всем видам продукции:
Каждый столбец этой матрицы соответствует дневной производительности отдельного предприятия по каждому виду продукции. Следовательно, годовая производительность J-Го предприятия по каждому виду продукции получается умножением J—Гo столбца матрицы А на количество рабочих дней в году для этого предприятия (J = 1, 2, 3, 4, 5). Таким образом, годовая производительность каждого предприятия по каждому из изделий описывается матрицей
Матрица затрат сырья на единицу изделия (эти показатели по условию одинаковы для всех предприятий) имеет вид
Дневной расход по типам сырья на предприятиях описывается произведением матрицы В на матрицу А:
Где I-я строка соответствует номеру типа сырья, а J-Й столбец — номеру предприятия согласно табл. 16.2 (I = 1, 2, 3; J = 1, 2, 3, 4, 5). Ответ на второй вопрос задачи получим по аналогии с матрицей АГод умножением столбцов матрицы ВА На соответствующие количества рабочих дней в году для предприятий — это годовая потребность каждого предприятия в каждом виде сырья:
Введем вектор стоимости сырья
Тогда стоимость общего годового запаса сырья для каждого предприятия получается умножением вектора 
Следовательно, суммы кредитования предприятий для закупки сырья определяются соответствующими компонентами вектора 
5. Отрасль состоит из П предприятий, выпускающих по одному виду продуции каждое; обозначим объем продукции I-го предприятия через Xi. Каждое из предприятий отрасли для обеспечения своего производства потребляет часть продукции, выпускаемой им самим и другими предприятиями. Например, в отрасли электротехнического оборудования часть продукции предприятий, выпускающих электродвигатели, силовые кабели, электрокары и т. д., употребляется практически всей отраслью. Пусть Aij — доля продукции I-го предприятия, потребляемая J-М предприятием для обеспечения выпуска своей продукции объема Xj. Возникает естественный вопрос о величине Yi — количестве продукции I-го предприятия, предназначенной для реализации вне данной отрасли (объем конечного продукта). Эта величина легко может быть подсчитана по формуле
Введем в рассмотрение матрицу порядка N, описывающую внутреннее потребление отрасли:
Тогда вектор конечного продукта является решением матричного уравнения
Или с использованием единичной матрицы Е получаем
Рассмотрим конкретный пример при П = 3. Пусть вектор выпуска продукции отрасли и матрица внутреннего потребления имеют соответственно вид
Используя формулу (16.1) и правило сложения матриц, получаем вектор объемов конечного продукта, предназначенного для реализации вне отрасли, состоящей из 3-х предприятий:
- Векторный метод в теории экономического анализа Текст научной статьи по специальности « Экономика и бизнес»
- Аннотация научной статьи по экономике и бизнесу, автор научной работы — Горюнов Е.В.
- Похожие темы научных работ по экономике и бизнесу , автор научной работы — Горюнов Е.В.
- Текст научной работы на тему «Векторный метод в теории экономического анализа»
- Применение векторов в повседневной жизни
- Просмотр содержимого документа «Применение векторов в повседневной жизни»
- 📽️ Видео
Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Векторный метод в теории экономического анализа Текст научной статьи по специальности « Экономика и бизнес»
Видео:Зачем нужен ВЕКТОР. Объяснение смыслаСкачать

Аннотация научной статьи по экономике и бизнесу, автор научной работы — Горюнов Е.В.
В работе представлены результаты исследований по разработке методики количественной оценки параметров вектора экономического развития. В качестве основного математического аппарата исследований использованы элементы теории векторной алгебры. Рассмотрен пример количественной оценки направления вектора экономического развития предприятия по шести общепринятым показателям.
Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Похожие темы научных работ по экономике и бизнесу , автор научной работы — Горюнов Е.В.
Видео:Умножение вектора на число. 9 класс.Скачать

Текст научной работы на тему «Векторный метод в теории экономического анализа»
векторный метод в теории
кандидат технических наук, доцент кафедры антикризисного управления E-mail: e_gorunov@mts-nn.ru Нижегородский государственный университет им. Н. ИЛобачевского
В работе представлены результаты исследований по разработке методики количественной оценки параметров вектора экономического развития. В качестве основного математического аппарата исследований использованы элементы теории векторной алгебры. Рассмотрен пример количественной оценки направления вектора экономического развития предприятия по шести общепринятым показателям.
Ключевые слова: вектор, метод, анализ, экономический процесс.
В практике анализа финансово-хозяйственной деятельности организаций используются такие понятия, как«вектор экономическогоразвития», «вектор инвестиций», «вектор инноваций» и др. При этом конечной целью анализа является определение направления движения этих векторов, прогнозирование развития процессов. Но, как правило, в результате анализа даются лишь качественные характеристики направлений вектора. Например: вектор экономического развития (ВЭР) направлен в сторону повышения фонда оплаты труда; ВЭР имеет направление в сторону роста реальных инвестиций»; ВЭР имеет направление в сторону роста инвестиций и инноваций и т.д.
При таких выводах не предусматривается количественной оценки того или иного вектора развития в его полном представлении.
Существуют задачи и модели, в которых прогнозирование развития процесса не представляет трудностей. Например, когда можно применить горизонтальный и вертикальный анализ системы показателей, полностью определенной по показате-
лям в виде элементарной суперпозиции. К анализу такой системы можно отнести, например, анализ бухгалтерского баланса, в котором арифметическая сумма значений строк составляет полный итоговый результат. В этом случае с позиции векторного анализа модель системы полностью определена в одномерном пространстве. Задача определения влияния факторов на результат и наиболее вероятных направлений развития организации, отображаемых в виде составляющих итога баланса, не считается сложной.
Пример 1. Выполним анализ вектора экономического развития организации (открытого акционерного общества) традиционным и разработанным автором способами.
Традиционный способ. Для анализа в соответствии с ПБУ 4/99 используем темпы роста за два года (п —1)и(й) следующих показателей темпов роста:
— собственных оборотных средств (7^);
— стоимости производственных фондов (Т6). Используем данные бухгалтерской отчетности,
представленные в работе [2]. Исходные и расчетные данные представлены в табл. 1.
Относительные изменения темпов роста показателей определяем по формуле:
отн I V ср и I V
где Т — среднее значение темпов роста показате-
Т. — темп роста /-го показателя.
Исходные и расчетные данные для анализа
Показатель (й-1) (и) Относительное изменение, %
Темп роста Относительное отклонение, % Темп роста Относительное отклонение, %
Т, 1,535 13,22 1,5 3,87 -9,35
Т2 3,042 -42,87 1,6 -9,88 32,99
Т, 1,548 12,27 1,3 10,92 -1,35
Т, 1,386 25,4 1,4 3 -22,4
Т, 1,866 -6,86 1,7 -15,8 -8,94
Те 1,05 65,52 1,15 25,39 -40,13
Среднее значение 1,738 — 1,442 — —
Уменьшение среднего темпа роста — — 1,205 — —
Из анализа табл. 1 можно сделать следующие выводы. В (п — 1) году над средним темпом роста превалировали темпы роста оборотных активов и темпы роста прибыли от реализации (3,042 и 1,866 соответственно). Темпы роста остальных показателей отставали. Если считать, что набор показателей характеризует процесс экономического развития предприятия, некий вектор развития, то можно сделать следующий вывод. В (п — 1) году вектор экономического развития был направлен в основном в сторону роста оборотных активов. При этом говорить об удельном весе вклада каждого из показателей некорректно, так как система показателей не полностью определена и показатели взаимосвязаны. Хотя можно говорить об относительном отклонении показателей от среднего значения. Да и средний темп роста показателей можно воспринимать условно. Более корректным явилось бы среднее значение темпов роста показателей во времени. Здесь налицо недостаток информации для анализа.
В (л) году превалировали темпы роста прибыли от реализации и темпы роста оборотных активов (1,7и 1,6 соответственно).
В целом в (л) году средний темп роста показателей уменьшился в 1,205 раза. Процесс экономического развития предприятия замедлился.
В традиционном способе горизонтального и вертикального анализа мы не получаем количественной оценки направления вектора экономического развития объекта исследования (предприятия).
Разработанный способ. Рассмотрим результаты исследований по предлагаемой методике количественной оценки параметров вектора моделей экономического развития. В качестве основного математического аппарата исследований используем элементы теории векторной алгебры [1], где
Рис 1. Модель вектора Ш в 3-мерном пространстве параметров
для описания любого вектора Ш в многомерном евклидовом векторном пространстве п параметров используются следующие количественные характеристики и параметры: длина вектора Ь, его проекции П1 на оси координат х и углы направлений а;. между вектором Ш и его проекциями на соответствующие оси ортогональной (взаимно перпендикулярной) системы координат (рис. 1).
Результирующий вектор Ш , отображенный на рис. 1, при этом является линейной суперпозицией составляющих его векторов:
Ж = Щ101 + П2 Х02 +. + Д. Х01 +. + пп х0и, где Х01. Х0п — ортогональные (взаимно перпендикулярные) и ортонормированные (единичные) векторы й-мерного пространства параметров;
Длина L вектора (на основании теоремы Пифагора в евклидовом пространстве):
L = [(Д)2 + (Л2)2 +. + (Пп )2 ]i (1)
Значения косинусов углов а;. между проекциями на оси координат вектора W можно представить в виде:
а, = arccos Д. /L, (3)
Угол главной биссектрисы (сумма биссект-рисных углов):
где а0 — результирующии угол, сумма углов направлений а;.
Соотношения (1) — (4) необходимы для выявления определенного эталонного значения вектора, относительно которого можно оценивать изменение вектора развития в дальнейшем.
Рассмотрим ситуацию, когда все значения параметров Д. равны между собой. Тогда Ь = 4пП1, а1 = а2 =. = а;. =. аи — все углы равны («золотая середина», биссектрисныеуглы).
В этом случае направление вектора Й формируется в равной степени всеми его составляющими, а длина вектора — минимальная. Например, длина вектора в прямоугольной (ортогональной) системе координат, когда вектор Й направлен под углом 45° к осям координат (под углом биссектрисы). Тогда Ь = 4пП1 = Д.
Значения биссектрисных углов а;. в случае равно направленности угловых составляющих вектора Й по отношению к осям координат и, соответственно, равенства параметров определяются с учетом формулы (3):
В случае, когда а1 = а2 =. = а;.=. аи, вектор Й будет направлен по главному биссектрисному углу.
Произведенные расчеты результирующих углов а0 направлений вектора Й и зависимость биссектрисных угловых параметров а;. от размерности п с использованием формул (5), (6) представлены в табл. 2.
Результирующий вектор Й в многомерном ортогональном пространстве координат при равенстве угловых составляющих проекций имеет минимальную длину Ь и направлен по углу главной биссектрисы в данном пространстве [1].
Из формул (1) — (3) следует, что изменение величины любой составляющей — проекции вектора на ось координат — приводит к изменению как длины Ь самого вектора Й , так и его направления в многомерном пространстве координат-параметров. При этом величины остальных проекций на оси координат также изменяются [1].
В задачах анализа направления развития экономических процессов приходится учитывать определенные особенности. Во-первых, факторы (параметры), определяющие направление развития экономического процесса, могут быть взаимосвязаны. Во-вторых, иногда невозможно разделить влияние действующих факторов, которые не поддаются объединению в одной модели. Поэтому при анализе изменения направления вектора экономического развития необходимо выбирать соответствующий инструмент измерения для оценки степени влияния факторов на формирование направления вектора с использованием его угловых и координатных параметров. В разработанном методе предлагается использовать для анализа вектора экономического развития длину вектора и угловые отклонения относительно биссектрисныхуглов вектора (табл. 2).
В рассматриваемом примере в векторном виде модель развития можно представить следующим образом:
й = Т+Т + Тз + г4 + Т + т6.
В этом примере мы проводим анализ вектора экономического развития в многомерном пространстве параметров — темпов роста шести показателей.
Зависимость биссектрисных углов вектора развития от размерности пространства параметров п, град.
N 2 3 4 5 6 7 8 9 10
а,. 45 54,75 60 63,6 65,9 67,7 69,3 70,5 71,6
«0 90 164,2 240 318 395,4 473,9 554,4 634,5 716
Расчетные данные представлены в табл. 3. Расчеты выполнены с использованием формул (3), (4).
Из анализа данных табл. 3 можно сделать следующие выводы:
— относительные изменения угловых параметров (направлений) результирующего вектора развития значительно меньше относительных изменений исходных параметров (проекций) — темпов роста. Если темпы роста показателей находятся в интервале 1,05—3,042 (изменяются в 2,9 раза), то их угловые параметры находятся в интервале 47,8—76,6град. (изменяются в 1,6 раза);
— превалирование одного из параметров — направление темпов роста оборотных активов в (й —1) году снизилось;
— угловые параметры а;. отличаются от значений углов аэ = 65,9град, (углов биссектрис).
Для анализа взаимосвязи изменения угловых параметров и изменения направления вектора развития примем за эталон угловой параметр — бис-сектрисный угол аэ вектора развития Ш в случае с равнонаправленными угловыми составляющими. В нашем случае в 6-мерном пространстве координат это значение аэ = 65,9град. (табл. 1).
Относительное отклонение ^для /-го параметра от эталонного аэ определяем по формуле
Результаты анализа изменения темпов роста показателей и изменения угловых параметров вектора развития исходя из выбранных шести показателей представлены в табл. 4.
Расчетные данные (табл. 4) показывают, с каким уровнем вклада в формирование направления вектора развития вносят угловые параметры каждого из значений темпов роста показателей. Знак (+) означает вклад в максимизацию длины вектора Ь и ускорения развития, при этом а;. Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
— за (й) год интенсивность развития экономического процесса уменьшилась. Длина вектора развития Ь уменьшилась с 4,529 до 3,616 (в 1,252 раза). Это обусловлено как снижением темпов роста отдельных показателей темпов роста, так и влиянием изменения их угловых параметров;
— если в (й— 1) году наибольший вклад в формирование направления и длины вектора развития давал показатель «темпы роста оборотных активов», то в последующем году этот вклад значительно уменьшился;
Расчетные значения параметров векторов развития
Показатель (и-1) (п) Изменение направления, град.
Темп роста а. град. Темп роста а. град.
т, 1,535 70,2 1,5 65,5 -4,7
Т2 3,042 47,8 1,6 63,8 16
Т, 1,548 70 1,3 68,9 -1,1
Т4 1,386 72,2 1,4 67,2 -5
Т, 1, 866 65,7 1,7 61,5 -4,2
Те 1,05 76,6 1,15 71,5 -5,1
Сумма углов направлений ап — 402,5 — 398,4 -4,1
Относительные отклонения угловых параметров показателей К от биссектрисных углов аэ вектора развития
Показатель (и-1) (и)
Темп роста Темп роста
т, 1,535 -6,13 1,5 +5,16
Т2 3,042 +37,87 1,6 +3,19
Т, 1,548 -5,86 1,3 -4,35
Т4 1,386 -8,73 1,4 -1,93
Т, 1, 866 +0,3 1,7 +7,15
Т6 1,05 -13,97 1,15 -7,83
— в предыдущем году наибольший вклад в минимизацию вектора развития дал показатель «темпы роста производственных фондов». В последующем году вклад этого показателя значительно уменьшился;
— за истекший период изменилось от отрицательного до положительного влияние темпов роста собственных оборотных средств. Снизилось влияние темпов роста краткосрочных обязательств и выручки от реализации. Возросло влияние темпов роста прибыли от реализации. Отмечается наибольшее изменение направления вектора развития в направлении темпов роста прибыли от реализации.
В целом направление вектора экономического развития предприятия изменилось ближе к главному биссектрисному углу а0 = 395,4 град. Длина вектора уменьшилась. Движение вектора экономического развития предприятия замедлилось в 1,252 раза.
Важно отметить следующее обстоятельство. В рассматриваемом примере средние темпы роста показателей уменьшились в 1,205 раза, в то время как длина вектора развития уменьшилась в 1,252 раза. При увеличении количества показателей (факторов модели) разница в результатах анализа по традиционному и предлагаемому способу может стать значительной. При этом достоверность традиционного анализа может существенно снижаться.
Пример 2. Выполним векторный анализ изменения конкурентоспособности товара по показателям «качество—цена». Векторную модель конкурентоспособности «качество—цена» представим в виде:
где К — интегральный вектор качества; С — цена товара.
Значение показателя качества Xопределяется экспертным путем.
При анализе ситуаций с различными значениями показателя качества Ки цены Стовара длину /-го вектора в /-Й ситуации на основании формулы (7) запишем в форме:
где Щ — 1-й показатель качества товара;
1 / С — значение обратной величины /-Й цены товара.
Используем для оценки показателей конкурентоспособности темпы роста (снижения) показателей качества и цены. Значения параметров векторов конкурентоспособности в данной задаче представлены в табл. 5.
Из данных табл. 5 можно сделать следующие выводы:
— наибольший рост конкурентоспособности товара наблюдается в ситуации, когда качество повышается на 10 %, а цена снижается на 20 %. Здесь Ь = 1,665; а2 Надоели баннеры? Вы всегда можете отключить рекламу.
Видео:СКАЛЯРНОЕ УМНОЖЕНИЕ ВЕКТОРОВ ЧАСТЬ I #математика #егэ #огэ #формулы #профильныйегэ #векторыСкачать

Применение векторов в повседневной жизни
С понятием вектора мы встречаемся чаще,чем сами подозреваем. В данной работе я постаралась максимально изучить, в каких же сферах мы взаимодействуем с ним.
Просмотр содержимого документа
«Применение векторов в повседневной жизни»
С уверенностью можно сказать, что мало кто из людей задумывается о том, что векторы окружают нас повсюду и помогают нам в повседневной жизни. Рассмотрим ситуацию: парень назначил девушке свидание в двухстах метрах от своего дома. Найдут ли они друг друга? Конечно, нет, так как юноша забыл указать главное: направление, то есть по-научному – вектор. Далее, в процессе работы над данным проектом, я приведу ещё множество не менее интересных примеров векторов.
Вообще, я считаю, что математика – это интереснейшая наука, в познании которой нет границ. Я выбрала тему о векторах не случайно, меня очень заинтересовало то, что понятие «вектор» выходит далеко за рамки одной науки, а именно математики, и окружает нас практически везде. Таким образом, каждый человек должен знать, что такое вектор, поэтому, я думаю, что эта тема весьма актуальна. В психологии, биологии, экономике и многих других науках употребляют понятие «вектор». Подробнее об этом я расскажу позже.
Целями данного проекта являются приобретение навыков работы с векторами, умение видеть необычное в обычном, выработка внимательного отношения к окружающему миру.
История возникновения понятия вектор
Одним из фундаментальных понятий современной математики является вектор. Эволюция понятия вектора осуществлялась благодаря широкому использованию этого понятия в различных областях математики, механики, а так же в технике.
Вектор относительно новое математическое понятие. Сам термин «вектор» впервые появился в 1845 году у ирландского математика и астронома Уильяма Гамильтона (1805 – 1865) в работах по построению числовых систем, обобщающих комплексные числа. Гамильтону принадлежат и термин «скаляр», «скалярное произведение», «векторное произведение». Почти одновременно с ним исследования в том же направлении, но с другой точки зрения вёл немецкий математик Герман Грассман (1809 – 1877). Англичанин Уильям Клиффорд (1845 – 1879) сумел объединить два подхода в рамках общей теории, включающий в себя и обычное векторное исчисление. А окончательный вид оно приняло в трудах американского физика и математика Джозайи Уилларда Гиббса (1839 – 1903), который в 1901 году опубликовал обширный учебник по векторному анализу.
Конец прошлого и начало текущего столетия ознаменовались широким развитием векторного исчисления и его приложений. Были созданы векторная алгебра и векторный анализ, общая теория векторного пространства. Эти теории были использованы при построении специальной и общей теории относительности, которые играют исключительно важную роль в современной физике.
Понятие вектора возникает там, где приходится иметь дело с объектами, которые характеризуются величиной и направлением. Например, некоторые физические величины, такие, как сила, скорость, ускорение и др., характеризуются не только числовым значением, но и направлением. В связи с этим указанные физические величины удобно изображать направленными отрезками. В соответствии с требованиями новой программы по математике и физике понятие вектора стало одним из ведущих понятий школьного курса математики.[2]
Векторы в математике
Вектором называется направленный отрезок, который имеет начало и конец.[1]




Два вектора называются коллинеарными, если они лежат на параллельных прямых, либо на одной прямой. Два вектора называются сонаправленными, если они коллинеарны и направлены в одну сторону, противоположно направленными, если коллинеарны и направлены в разные стороны.
Операции над векторами




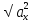
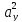
В координатном представлении вектор суммы получается суммированием соответствующих координат слагаемых:

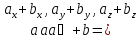

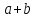


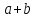
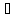

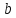
Это правило прямо и естественно обобщается для сложения любого количества векторов, переходя в правило ломаной:
Начало второго вектора совмещается с концом первого, начало третьего — с концом второго и так далее, сумма же 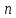
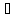

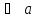
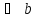
Правило параллелограмма особенно удобно, когда есть потребность изобразить вектор суммы сразу же приложенным к той же точке, к которой приложены оба слагаемых — то есть изобразить все три вектора имеющими общее начало.
Для получения разности в координатной форме надо вычесть соответствующие координаты векторов:




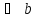
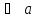
Умножение вектора на число



Скалярное произведение векторовСкалярное
Скалярным произведением называют число, которое получается при умножении вектора на вектор. Находится по формуле:

Скалярное произведение можно найти ещё через длину векторов и угол между ними. 
Применение векторов в смежных науках Векторы в физике Векторы — мощный инструмент математики и физики. На языке векторов формулируются основные законы механики и электродинамики. Чтобы понимать физику, нужно научиться работать с векторами. В физике, как и в математике, вектор – это величина, которая характеризуется своим численным значением и направлением. В физике встречается немало важных величин, являющихся векторами, например сила, положение, скорость, ускорение, вращающий момент, импульс, напряженность электрического и магнитного полей. Векторы в литературе Вспомним басню Ивана Андреевича Крылова о том, как «лебедь, рак да щука везти с поклажей воз взялись». Басня утверждает, что «воз и ныне там», другими словами, что равнодействующая всех сил приложенных к возу сил равна нулю. А сила, как известно, векторная величина. Векторы в химии
Нередко даже великими учеными высказывалась мысль, что химическая реакция является вектором. Вообще-то, под понятие «вектор» можно подвести любое явление. Вектором выражают действие или явление, имеющее четкую направленность в пространстве и в конкретных условиях, отражаемое его величиной. Направление вектора в пространстве определяется углами, образующимися между вектором и координатными осями, а длина (величина) вектора – координатами его начала и конца.
Однако утверждение, что химическая реакция является вектором, до сих пор было неточно. Тем не менее основой этого утверждения служит следующее правило: «Любой химической реакции отвечает симметричное уравнение прямой в пространстве с текущими координатами в виде количеств веществ (молей), масс или объемов».
Все прямые химических реакций проходят через начало координат. Любую прямую в пространстве нетрудно выразить векторами, но поскольку прямая химической реакции проходит через начало системы координат, то можно принять, что вектор прямой химической реакции находится на самой прямой и называется радиус-вектором. Начало этого вектора совпадает с началом системы координат. Таким образом, можно сделать вывод: любая химическая реакция характеризуется положением ее вектора в пространстве. Векторы в биологии
Вектором (в биологии) называется организм, переносящий паразита от одного организма-хозяина к другому. Например, вши переносят возбудителей сыпного тифа, крысы – чумы.
Вектор (в генетике) — молекула нуклеиновой кислоты, чаще всего ДНК, используемая в генетической инженерии для передачи генетического материала другой клетке.
Векторы в экономике
Одним из разделов высшей математики является линейная алгебра. Ее элементы широко применяются при решении разнообразных задач экономического характера. Среди них важное место занимает понятие вектора.
Вектор представляет собой упорядоченную последовательность чисел. Числа в векторе с учетом их расположения по номеру в последовательности называются компонентами вектора. Отметим, векторы можно рассматривать в качестве элементов любой природы, в том числе и экономической. Предположим, что некоторая текстильная фабрика должна выпустить в одну смену 30 комплектов постельного белья, 150 полотенец, 100 домашних халатов, тогда производственную программу данной фабрики можно представить в виде вектора, где всё, что должна выпустить фабрика – это трехмерный вектор.
Векторы в психологии
На сегодняшний день имеется огромное количество информационных источников для самопознания, направлений психологии и саморазвития. И не трудно заметить, что все больше обретает популярность такое необычное направление, как системно-векторная психология, в ней существует 8 векторов.
Векторы в повседневной жизни
Я обратила внимание, что векторы, помимо точных наук, встречаются мне каждый день. Так, например, во время прогулки в парке, я заметила, что ель, оказывается, можно рассматривать как пример вектора в пространстве: нижняя её часть – начало вектора, а верхушка дерева является концом вектора. А вывески с изображением вектора при посещении больших магазинов помогают нам быстро найти тот или иной отдел и сэкономить время.
Векторы в знаках дорожного движения
Каждый день, выходя из дома, мы становимся участниками дорожного движения в роли пешехода либо в роли водителя. В наше время практически каждая семья имеет машину, что, разумеется, не может не отразиться на безопасности всех участников дорожного движения. И, чтобы избежать казусов на дороге, стоит соблюдать все правила дорожного движения. Но не стоит забывать того, что в жизни всё взаимосвязано и, даже в простейших предписывающих знаках дорожного движения, мы видим указательные стрелки движения, в математике называемые – векторами. Эти стрелки (векторы) указывают нам направления движения, стороны движения, стороны объезда, и ещё многое другое. Всю эту информацию можно прочитать на знаках дорожного движения на обочинах дорог.
Базовое понятие «вектор», рассмотренное нами ещё на уроках математики в школе, является основой для изучения в разделах общей химии, общей биологии, физики и других наук. Я наблюдаю необходимость векторов в жизни, которые помогают найти нужный объект, сэкономить время, они выполняют предписывающую функцию в знаках дорожного движения.
Каждый человек постоянно сталкивается с векторами в повседневной жизни.
Векторы необходимы нам для изучения не только математики, но и других наук.
📽️ Видео
Аналитическая геометрия, 1 урок, Векторы в пространствеСкачать

ВЕКТОРЫ 9 класс С НУЛЯ | Математика ОГЭ 2023 | УмскулСкачать

Векторы для чайников (что потребуется знать при решении физических задач)Скачать

Математика это не ИсламСкачать

Математика без Ху!ни. Угол между векторами, применение скалярного произведения.Скачать

Выразить векторы. Разложить векторы. Задачи по рисункам. ГеометрияСкачать

Что такое вектора? | Сущность Линейной Алгебры, глава 1Скачать

Арктическое судоходство: механизмы повышения эффективности и векторы развития. Канатаев Денис, ДВМПСкачать

➡️ КАК ВЫЧИТАТЬ ВЕКТОРЫ?Скачать

Как разложить вектор по базису - bezbotvyСкачать

8 класс, 48 урок, Применение векторов к решению задачСкачать

Геометрия - 9 класс (Урок№1 - Понятие вектора. Равенство векторов)Скачать

АЛГЕБРА С НУЛЯ — Что такое Производная?Скачать

ПРОИЗВОДНАЯ функции. Объяснение математического смысла.Скачать

87. Применение векторов к решению задачСкачать