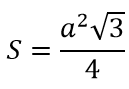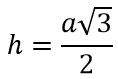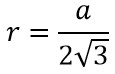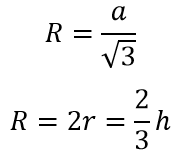Основание треугольника – это такая же сторона, как и две других. Основание редко имеет особое значение, но из-за визуальной обособленности от других сторон, ученики часто путаются и допускают ошибки. Разберем подробнее, как сторона треугольника может считаться основанием, и в каких случаях это действительно имеет значение
Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Стороны треугольника
У треугольника всегда три стороны. Одна из них считается основанием. Как правило, основание выделяется только построением, т.е. нижняя сторона треугольника, и приниматься за основание.
Иногда в решении указывают углы при основании произвольного треугольника. Это не совсем верно, поскольку в произвольном треугольнике все углы равнозначны, а значит не имеет смысла выделять углы при основании. Выделяются только углы при основании равнобедренного треугольника.
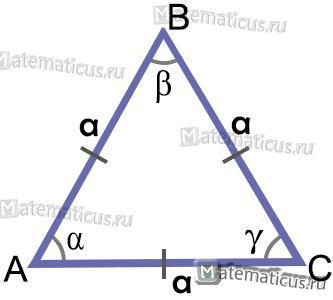
Рис. 1. Углы произвольного треугольника.
Нужно учитывать, что любой произвольный треугольник можно условно перевернуть, т.е. перечертить фигуру таким образом, чтобы основанием стала другая сторона. По этому разделять понятие боковых сторон и основания у произвольного треугольника не имеет смысла – это только добавит путаницы в решение задачи.
Уравнение основания треугольника, так же, как и уравнение любой из сторон треугольника, является уравнением прямой линии.
Видео:НАЙДИТЕ ВЫСОТУ РАВНОСТОРОННЕГО ТРЕУГОЛЬНИКАСкачать

Равнобедренный треугольник
Равнобедренный треугольник – это единственный подвид треугольника, где основание имеет реальное практическое значение. Равнобедренным треугольником называется треугольник, у которого две стороны равны между собой. Равные стороны зовутся боковыми, а третья сторона считается основанием.
Существует две теоремы об основании равнобедренного треугольника. Это:
- Теорема о равенстве углов: в равнобедренном треугольнике углы при основании равны.
- Теорема о равенстве медианы, биссектрисы и высоты, проведенной к основанию. Теорема особенно подчеркивает, что из трех возможных медиан, высот и биссектрис, только проведенные к основанию окажутся равными между собой.
В равнобедренном треугольнике основание определяется значением сторон: равные стороны – боковые, неравная – основание.
Рис. 2. Равнобедренный треугольник.
По ходу решения задачи может получится так, что основание окажется сбоку, не нужно этого пугаться. Стоит или привыкнуть к такому построению равнобедренного треугольника или каждый раз перечерчивать чертеж, разворачивая треугольник в нужную сторону.
Видео:Формулы равностороннего треугольника #shortsСкачать

Равносторонний треугольник
Равносторонний треугольник – это частный случай равнобедренного. У равнобедренного треугольника равны две стороны, а у равностороннего все три. Но именно из-за этого свойства значение основания равнобедренного треугольника теряется.
В равностороннем треугольнике какую сторону не выбери: две другие всегда будут равны между собой, а значит любая сторона может считаться основанием.
Рис. 3. Равносторонний треугольник.
Существует формула, где часто упоминается слово основание. Это формула площади, которая равна половине произведения основания треугольника на высоту, проведенную к этому основанию. Но в качестве основания может быть принята любая сторона, главное, чтобы именно на нее падала высота. Поэтому и в этом случае выбор стороны треугольника, которую можно считать основанием, некритичен.
Видео:По силам каждому ★ Найдите стороны треугольника на рисункеСкачать

Что мы узнали?
Мы узнали, что такое основание треугольника. Поговорили о ситуациях, когда стоит выделять основание среди других сторон треугольника, а когда это окажется напрасной тратой времени. Обсудили значимость основания равнобедренного треугольника.
Видео:№706. Найдите сторону равностороннего треугольника, если радиус описанной около него окружностиСкачать

Как найти основание треугольника
Для того, чтобы найти основание треугольника, можно воспользоваться одной из формул, обязательно должны быть заданы для этой формулы площадь и высота. Вообще, в геометрии и тригонометрии нет четкого обозначения того, какая именно сторона является основанием, так как его можно перевернуть на любую из них. Чтобы найти основание треугольника, его для начала нужно обозначить, а именно выделить ту сторону, на противоположном от которой углу расположена высота. Это перпендикуляр по отношению к основанию, и в зависимости от типа треугольника, он может делить основание пополам.
Есть ряд основных формул, по которым можно найти основание треугольника, в том числе и равнобедренного. Основная формула выглядит так:
- S – площадь треугольника;
- С – длина основания треугольника, которую надо найти;
- h – высота треугольника.
Исходя из тех данных, которые у нас есть, можно найти основание треугольника, если дана площадь и высота.
Видео:Периметр треугольника. Как найти периметр треугольника?Скачать

Как найти основание равнобедренного треугольника
По этой же формуле можно найти основание равнобедренного треугольника. Если известна одна сторона и значение угла напротив основания, то можно вывести по формуле высоту треугольника и потом найти основание по общей формуле.
Видео:Сможешь найти основание? Задача про медиану равнобедренного треугольникаСкачать
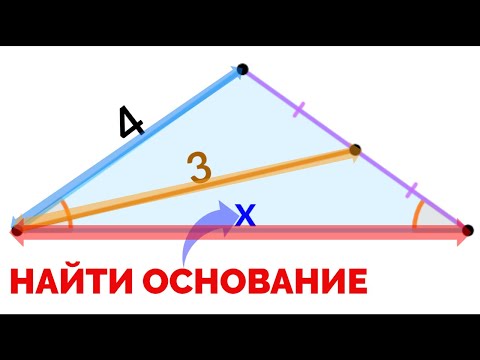
Как найти основание равностороннего треугольника через косинус
Если известны боковая сторона и величина противоположного основанию угла, можно найти основание треугольника через формулу, где используется значение косинуса.
- С – величина противоположного основанию угла равностороннего треугольника;
- А – длина боковой стороны треугольника;
- с – длина основания.
Эта формула для того, чтобы найти основание треугольника, основана на теореме косинусов и имеет более известную и более простую для применения формулу с=2*а*sin(B/2).
А еще интересно знать, стоит ли покупать евро, так как валюта постоянно дорожает.
Видео:Площадь равностороннего треугольника #егэ #математика #геометрия #треугольникСкачать

Равносторонний (правильный) треугольник
Равносторонний или правильный треугольник — треугольник, у которого три стороны равны. Все углы равностороннего треугольника равны.
Равносторонним треугольником называется такой треугольник, у которого все стороны равны, то есть АВ = ВС = АС (рис. 1)
Свойства равностороннего (правильного) треугольника
- Все углы равностороннего треугольника равны по 60°
∠А=∠С=∠В=60°
- Биссектрисы треугольника являются медианами и высотами, то есть равны и точка их пересечения, является центром вписанной окружности (рис. 2).
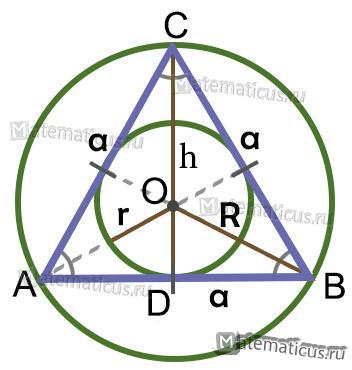
Из (рис. 2) обозначения:
h — высота=биссектриса=медиана
R — радиус описанной окружности
r — радиус вписанной окружности
a — стороны правильного треугольника
Формула периметра равностороннего треугольника:
P=3·a
Формула площади правильного треугольника:
Формула высоты (или медианы или биссектрисы) равностороннего треугольника:
Радиус вписанной окружности в равносторонний треугольник:
Радиус описанной окружности в равносторонний треугольник:
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 4.6 / 5. Количество оценок: 5
🎥 Видео
Известна биссектриса равностороннего треугольника. Найти сторону этого треугольника. ОГЭ №16Скачать

Высота, биссектриса, медиана. 7 класс.Скачать

7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

Задача найти сторону равностороннего треугольника по медианеСкачать

Геометрия Равносторонний треугольникСкачать

Как найти сторону равностороннего треугольника #shorts | ЕГЭ 2022 по профильной математике | ЭйджейСкачать

Нахождение стороны прямоугольного треугольникаСкачать

Задание 15 ОГЭ. Медиана равностороннего треугольникаСкачать

№488. Найдите: а) высоту равностороннего треугольника, если его сторона равна 6 см;Скачать

Площадь равностороннего треугольникаСкачать

ОГЭ 16🔴Скачать

№204. Прямая ОМ перпендикулярна к плоскости правильного треугольника ABC и проходит через центр ОСкачать