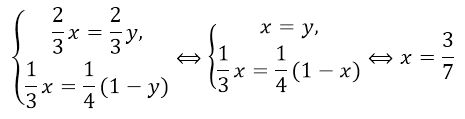Использование координат и векторов для решения математических задач

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Применение векторов и координат для решения задач

Одним из универсальных приемов решения геометрических задач является метод координат. Кроме этого, часто (особенно при доказательстве различных неравенств) используется векторный метод.

Вы уже хорошо знакомы с векторами, координатами и их свойствами. Цель нашей работы: научиться применять знания для решения задач. Здесь большое значение имеет опыт: чем с большим числом приемов решений и доказательств вы ознакомились – тем “мощнее” ваш арсенал.

Дадим несколько общих указаний, которые помогут сориентироваться и решить, можно ли в данной задаче использовать векторы и координаты:

Во-первых, естественно, нужно применять координатный или векторный метод, если в условиях задачи говорится о векторах или координатах;

Во-вторых, координатный метод может помочь, если в задаче требуется определить геометрическое место точек (т. е. спрашивается, какую фигуру образуют точки, удовлетворяющие некоторому условию);

В-третьих, очень полезно применить координатный метод, если из условия задачи не понятно, как расположены те или иные точки;

В-третьих, полезно и удобно применять координаты и векторы для вычисления углов и расстояний;

В-четвертых, вообще, часто, когда не видно ни каких подходов к решению задачи, или вы не можете составить уравнения, попробуйте применить координатный метод. Он не обязательно даст решение, но поможет разобраться с условиями и даст толчок к поиску другого решения.

Вооружившись этими советами и повторив материал по школьному учебнику геометрии[1], вы можете двигаться дальше. В следующем параграфе изложен материал, который не включен в школьный учебник, но может быть весьма полезен нам в дальнейшем.

§2 Свойства и теоремы о векторах и координатах на плоскости

п.1. Разные способы определения координат точки на плоскости

1.1. В математике используется два способа введения координат. В первом случае используются понятия: “систе­ма координат”, “координатные оси”, “координаты точки”. Тогда координаты точки определяются как координаты ее проекций на координатные оси (ОХ) и (OY). Аналогично определяются и координаты вектора. Остановимся на этом по подробнее: В прямоугольной системе координат векторы , и отложим от точки О – начала координат (см. Рис. 1). В этом случае координаты вектора совпадают с координатами точки А в рассматриваемой системе координат. Поэтому координаты вектора вычисляются как координаты его конца – точки А.

Во “взрослой” математике применяется другой способ определения координат точки. Познакомимся с ним. Рассмотрим вектор, начало которого находится в начале координат, а конец – в некоторой точке А. Вектор называют радиус-вектором точки А. Коэффициенты разложения радиус-вектора по векторам и мы и будем называть координатами точки А.

Такое определение может показаться ненужным, с его помощью координаты построенной на чертеже точки не найдешь. Но оно позволяет применять аппарат векторной алгебры для работы с координатами точек. В этом читатель может убедиться, познакомившись с примерами.

Пример 1. Пусть нам даны координаты точек М1 и М2: М1(х1; у1), М2(х2; у2). Надо найти координаты точки М, такой, что (где λ – некоторое действительное число, не равное -1).

Решение: При изучении темы “Векторы” в 8 классе вы узнали, что для любой точки О и указанных выше точек М1, М2 и М имеет место векторное равенство:

(2.1)

Выберем точку О так, чтобы она совпала с началом координат. Тогда векторы , и и будут радиус-векторами точек М1, М2 и М и их координаты будут совпадать с координатами самих точек.

Применим к уравнению (2.1) известные правила действий над векторами в координатах. Мы получим для координат (х; у) вектора следующие выражения:

(2.2)

Так как координаты радиус-вектора равны координатам точки, то формулы (2.2) дают нам искомое решение.

Следующий пример показывает, как можно задать координаты точек, лежащих на некоторой прямой.

Пример 2. Пусть нам известны координаты двух разных точек А и В (А(х1; у1), В(х2; у2)). Требуется выразить через них координаты (x, y) любой точки М, лежащей на прямой АВ.

Решение: Конечно, мы можем попробовать составить уравнение прямой так, как этому вас учат на уроках алгебры. Однако попробуем векторный метод. На рисунке 2 вы видите, что радиус-вектор точки М – вектор по правилу треугольника можно представить в виде суммы . Обратим также внимание на то, что векторы и коллинеарны, и значит (по признаку коллинеарности) , где t – некоторое число. Заметим также, что , поэтому окончательно получим:

.

Для координат (х; у) точки М имеем:

(2.3)

Замечание 1. В примере мы изначально считаем, что число t — любое. Если же ввести ограничение 0≤t≤1, то получатся координаты всех точек отрезка АВ.

Замечание 2. Уравнения (2.3) называют параметрическими уравнениями прямой (число t – параметр).

Параметрические уравнения прямой можно получить и по другому. Параметрические уравнения прямой, проходящей через точку М0(х0; у0) и параллельной вектору имеют вид

(2.3’)

п.2. Длина вектора и отрезка

Напомним, что если вектор имеет координаты (а1; а2), то его длина равна: (2.4)

Если известны координаты концов отрезка (А(х1; у1), В(х2; у2)), то его длина равна:

(2.5)

Обратим внимание читателей еще на один интересный факт, связанный с координатами вектора единичной длины.

Пример 3. Найдите координаты единичного вектора , если он составляет с осью ОХ угол .

Решение: Отложим единичный вектор от начала координат. Пусть .

Координаты точки М (а значит, и вектора ) равны и , где М1 и М2 – проекции точки М на координатные оси. Рассмотрим прямоугольный треугольник ОМ1М. Его прилежащий катет ОМ1=×cosa. Заметим, что по условию. Таким образом, =cosa. Теперь рассмотрим : т. к. ОМ1ММ2 – прямоугольник, то .

С другой стороны, М1М – противолежащий катет треугольника ОМ1М, и его длина равна: . Отсюда и . Таким образом, координаты вектора такие: (2.6)

Замечание: Мы рассмотрели случай, когда лежит в I-ом координатном угле. Другие случаи можно рассмотреть аналогично.

1.1. Напомним, что для длин векторов выполняется неравенство треугольника: (2.7)

Как следствие, длина суммы двух единичных векторов не больше двух, а длина суммы n единичных векторов не превосходит число n:

, где все (2.8)

п.3 Векторы и многоугольники

3.1. В некоторых задачах на векторы требуется выяснить, можно ли из данных векторов составить многоугольник. Поясним, что это означает: векторы откладываются так, что конец предыдущего является началом следующего. Если конец последнего вектора совпадет с началом первого, то “цепочка” замкнется и получится замкнутая ломаная. Это и означает, что из векторов можно построить многоугольник.

Алгебраически это означает, что сумма рассматриваемых векторов равна нулевому вектору: (2.9)

Замечание: Иногда это условие заменяется другим: один из векторов равен сумме остальных, т. е. (2.10)

4.1. Иногда встречаются задачи, в которых рассматриваются точки, координаты которых – целые числа. Такие точки принято называть узлами и вот почему. Отметим на оси ОХ точки с целыми координатами и проведем через них прямые, параллельные оси ОY. Затем также поступим с аналогичными точками оси OY. В результате мы получим “решетку”, каждая “ячейка” которой – квадрат со стороной, равной единице. Точки с целыми координатами будут служить вершинами ячеек – узлами.

4.2. Если параллелограмм имеет целочисленные вершины, и одна из его сторон параллельна какой-нибудь координатной оси, то площадь параллелограмма – целое число.

Чтобы убедиться в этом, посмотрим на рисунок 5. Мы видим, что параллелограмм АВСD и прямоугольник АВС1D1 имеют общее основание АВ и равные высоты. Очевидно, что если координаты вершин прямоугольника – целые числа, то его длина и высота – также целые числа. Значит и площадь прямоугольника – целое число. С другой стороны, площадь параллелограмма равна площади прямоугольника. Значит она тоже целое число.

Замечание: Мы далее получим формулу, из которой следует, что у любого параллелограмма с целочисленными вершинами, площадь – целое число.

п.5. Скалярное произведение векторов

5.1. Скалярным произведением векторов и называется число, равное произведению длин этих векторов на косинус угла между ними:

(2.11)

5.2. Скалярное произведение в координатах находим по формуле:

(2.12)

здесь .

5.3. Если векторы перпендикулярны, то их скалярное произведение равно нулю.

^ Û ).

5.4. Пример 4. Для вектора найдите перпендикулярный, равный ему по длине.

Решение: Рассмотрим векторы и . Очевидно, что (формула 2.4). Легко убедиться, что ^. Действительно, Þ ^. Аналогично показывается, что ^.

Таким образом, и – искомые векторы.

5.5. Угол между векторами вычисляется по формуле (2.13)

В координатах эта формула имеет вид: (2.14)

5.6. Из определения синуса и косинуса угла в прямоугольном треугольнике следует, что для его острых углов a и b имеют места равенства и . Так как b=90°-a (из свойств углов прямоугольного треугольника), то и . (2.15)

Найдем формулу для вычисления площади параллелограмма, построенного на векторах и . Воспользуемся известной формулой для вычисления площади параллелограмма: (*). Из рисунка 6 видно, что и . Поэтому по формуле (2.4) . Нам теперь нужно найти sina. Поступим следующим образом. Рассмотрим векторы и из пункта (5.4). На чертеже 6 видно, что один из углов , или равен 90°-a. (Какой именно, зависит от того, с какой стороны от лежит вектор . Если и лежат по одну сторону от , берем первый угол, если по разные стороны – второй).

Найдем . Используем формулы (2.14)

Подставим все найденные значения в формулу (*). Получим окончательное выражение для площади параллелограмма:

Итак (2.16)

п.6 Задание геометрического места точек аналитическим условием на их координаты.

6.1. Вы уже знаете, что некоторые геометрические фигуры можно задать уравнением. Например: прямая задается (в прямоугольной системе координат) уравнением y=kx+b, а окружность с центром в точке M0(x0, y0) и радиусом R, задается уравнением: (x-x0)2+(y-y0)2=R2.

С другой стороны, геометрическую фигуру можно задать как геометрическое место точек, например:

· множество точек, удаленных от данной точки на расстояние R (окружность),

· множество точек, равноудаленных от концов данного отрезка (серединный перпендикуляр к отрезку),

· множество точек, равноудаленных от сторон угла (прямая, содержащая биссектрису этого угла).

Ниже мы рассмотрим более сложные примеры геометрических мест точек.

Теперь подробнее остановимся на понятии “аналитическое условие”. Задать фигуру аналитическим условием, значит в некоторой системе координат найти уравнения или неравенства, которым удовлетворяют координаты точек этой фигуры.

Система неравенств задает на координатной плоскости квадрат, длины сторон которого равны двум, центр совпадает с началом координат, а стороны параллельны осям координат.

6.3. В геометрии можно рассматривать три основных задачи:

· отыскание аналитических условий для некоторого геометрического места точек,

· определение по аналитическим условиям вида и строения геометрического места точек (что собой представляет данное множество, какая это фигура –окружность, отрезок, луч и т. п.),

· использование аналитических условий для исследования геометрических свойств фигуры.

В рамках данной статьи мы ограничимся рассмотрением нескольких примеров нахождения аналитических условий.

§ 3. Примеры решения задач

3.1. Даны координаты вершин треугольника АВС: А(1, 0), В(4, -3), С(12, 5). Точки М и N лежат на сторонах АВ и ВС соответственно и делят их в одинаковом отношении 1:2. Найдите координаты середины отрезка MN.

Из чертежа (рис. 7) и условия задачи следует, что и . Найдем координаты точек М и N по формулам (2.2):

Теперь, зная координаты концов отрезка MN, найдем координаты его середины:

Ответ: .

3.2. На сторонах треугольника АВС построены параллелограммы AKLB, BMNC и CPQA (рисунок 8). Можно ли составить треугольник из векторов и ?

Сумма векторов , так как они образуют замкнутый контур. Так как и , то из первого равенства получаем, что . А из п. 3.1. следует, что эти векторы могут составить треугольник.

3.3. Не производя построение, определите, являются ли точки А (1, 2), В (6, -2), С (3, 4) и

D (-12, 0) вершинами выпуклого четырехугольника.

Необходимым и достаточным условием того, что четырехугольник выпуклый, является то, что отрезки АС и BD – диагонали – пересекаются (рисунок 9). Составим параметрические уравнения отрезков АС и BD:

Приравняем координаты и , тогда мы получим два уравнения относительно неизвестных и . Найдем их решения. Если выполнены условия и , то точка пересечения прямых AC и BD лежит внутри обеих диагоналей, значит, диагонали пересекаются и четырехугольник – выпуклый. Если хотя бы одно условие нарушено, четырехугольник не выпуклый. Итак:

Мы видим, что t1 не удовлетворяет условию 0 b) – полуосями эллипса.

Задание для самостоятельного решения

Необходимо решить предложенные ниже задачи, оформить их решения отдельно от заданий по другим предметам и выслать в адрес Хабаровской краевой заочной физико-математической школы.

М.10.11.1. Докажите, что прямая, проходящая через точку М1(х1; у1) и М2(х2; у2) может быть задана уравнением .

Указание: в уравнениях (2.3) §2 выразите параметр t и приравняйте правые части.

М.10.11.2. Векторы и образуют угол, докажите, что вектор лежит на биссектрисе этого угла.

М.10.11.3. Даны координаты вершин треугольника: А(0; 1), В(1; 0), С(6; -3), найдите параметрические уравнения биссектрисы угла .

Указание: используйте результаты задач М.10.8.1 и М.10.8.3.

М.10.11.4. В условиях задачи 3.1.2 из §3 проверьте, могут ли векторы и служить сторонами треугольника.

М.10.11.5. АВСD – ромб со стороной 2 см и углом при вершине А в 60°. Введите систему координат, поместив ее начало в т. А, направив ось ОХ по прямой АВ, а ось OY – перпендикулярно к АВ, в ту сторону, с которой лежит сам ромб. Найдите координаты всех вершин ромба и точки пересечения его диагоналей.

М.10.11.6. Точки А(7; -1) и С(3; 0) – противоположные вершины прямоугольника АВСD. Найдите координаты двух других вершин, если стороны прямоугольника параллельны координатным осям.

М.10.11.7. Окружности радиусов r и R касаются внешним образом, прямая а – их общая касательная. Найдите радиус окружности, которая касается двух данных и прямой а.

М.10.11.8. Докажите, что площадь параллелограмма, координаты всех вершин которого – целые числа, целое число.

М.10.11.9. Решите систему

Указание: рассмотрите векторы с координатами (х; ) и (у; ), тогда левые части уравнений системы есть координаты суммы двух этих векторов. Рассмотрите длины трех этих векторов и убедитесь (докажите), что два первых – равны.

М.10.11.10. Докажите, что все точки параболы обладают следующим свойством: расстояние от любой точки M параболы до точки F(0,p) равно расстоянию от точки M до прямой .

(Точку F называют фокусом параболы, а прямую — директрисой.)

М.10.11.11. Сколько точек с целочисленными координатами лежит внутри треугольника АВС если вершины имеют координаты: А(1,-1), В(3,-8), С(11,6).

[1] Повторите материал из главы IX, X и §3 главы XI из учебника геометрии 7-9, авторов и др.

[2] Обращаем внимание читателей, что с термином “решетка” в математике связано несколько разных понятий.

Видео:Векторы. Метод координат. Вебинар | МатематикаСкачать

План-конспект практического занятия «Использование координат и векторов при решении математических и прикладных задач»
план-конспект занятия по математике (11 класс)

Раздел 3. Геометрия

Тема 3.5. Координаты и векторы

Занятие 31. Использование координат и векторов при решении

математических и прикладных задач

Цель занятия: ознакомление с использованием координат и векторов при решении математических и прикладных задач

Задачи занятия:

Обучающая: научить учащихся использовать знания о координатах и векторах при решении прикладных задач в физике и геометрии; полученные ранее знания научиться использовать как инструмент для решения прикладных задач развивать интерес учащихся к изучению математики и физики;

Воспитательная: воспитание внимательности, аккуратности.

Развивающая: развитие пространственного воображения, умения самостоятельной работы с учебной литературой развитие абстрактного мышления, пространственного воображения и интуиции, развитие познавательного интереса.

Видео:Координаты вектора. 9 класс.Скачать

Скачать:

Видео:8 класс, 48 урок, Применение векторов к решению задачСкачать

Предварительный просмотр:

ДЕПАРТАМЕНТ ОБРАЗОВАНИЯ И НАУКИ ГОРОДА МОСКВЫ

Государственное бюджетное профессиональное образовательное учреждение города Москвы

(ГБПОУ Юридический колледж)

ПЛАН-КОНСПЕКТ учебного занятия

по ОУДб.04 Математика

учебной дисциплине/междисциплинарному курсу

для обучающихся курс 1

Раздел 3. Геометрия

Тема 3.5. Координаты и векторы

Занятие 31. Использование координат и векторов при решении

математических и прикладных задач

Цель занятия: ознакомление с использованием координат и векторов при решении математических и прикладных задач

Обучающая : научить учащихся использовать знания о координатах и векторах при решении прикладных задач в физике и геометрии; полученные ранее знания научиться использовать как инструмент для решения прикладных задач развивать интерес учащихся к изучению математики и физики;

Воспитательная: воспитание внимательности, аккуратности.

Развивающая: развитие пространственного воображения, умения самостоятельной работы с учебной литературой развитие абстрактного мышления, пространственного воображения и интуиции, развитие познавательного интереса.

1. Геометрия: Учебник для 10-11 классов общеобразовательных учреждений / Л.С. Атанасян, В.Ф. Бутузов и др. М., Просвещение, 2019.

1. Башмаков М.И. Математика. М., «Академия», 2019

2. Богомолов Н.В. Сборник задач (учебное пособие) – М.: Дрофа, 2019.

Образовательный портал Решу ЕГЭ.

Единая коллекция цифровых образовательных ресурсов

Открытый банк заданий по математике

Информационные, тренировочные и контрольные материалы.

Междисциплинарные связи: алгебра и начала анализа, физика, естествознание

Внутридисциплинарные связи: геометрия

1.АКТУАЛИЗАЦИЯ РАНЕЕ ИЗУЧЕННОГО МАТЕРИАЛА УЧЕБНОГО КУРСА

(ответить на вопросы (тестовые задания) и провести самооценку усвоенного материала)

1. Сформулируйте определение сонаправленных векторов.
2. Сформулируйте определение компланарных векторов.
3. Запишите формулу для нахождения скалярного произведения векторов.
4. Запишите вектор АВ, если точка А(1;-2;3) и В(0;-6;4)
5. Сформулируйте правило треугольника для сложения векторов

2. ИЗУЧАЕМЫЕ ВОПРОСЫ УЧЕБНОГО ЗАНЯТИЯ

1. Использование координаты и векторов при решении математических и прикладных задач

Вопрос 1. Использование координаты и векторов при решении математических и прикладных задач

На прошлых занятиях мы познакомились с тем, что такое, координаты, вектор, плоскость и пространство. Как задается точка, отрезок, вектор на плоскости и в пространстве. Научились совершать различные действия над векторами. Вектор — многозначный термин; величина, характеризующаяся размером и направлением. Вектора применяются во многих науках, таких как: математика, физика, геометрия и многих других прикладных науках.

Векторы вокруг нас! Нам безусловно важно знать в каком направлении мы движемся: вошли мы в класс или вышли, в каком направлении повернули ручку конфорки духового шкафа когда там начинает подгорать пирог…. Все это вектора, и они играют важную роль в нашей жизни. На практике, векторы позволяют не делать лишних операций и сократить время выполнения задач. Сегодня подводим итоги изучаемой темы.

Проверочная работа по теме: « Координаты и векторы »

1. Дан вектор . Напишите координаты вектора
2. Упростите выражение:
3. Упростите выражение:
4. Упростите выражение:
5. Найдите координаты вектора , если
6. Даны векторы , найдите
7. Даны векторы , найдите
8. О начало координат, F (5;-1,0). Найдите координаты вектора
9. Дан вектор найдите длину
10. Даны векторы , найдите координаты вектора
11. Найдите скалярное произведение векторов и
12. Найдите скалярное произведение векторов и
13. Найдите скалярное произведение векторов и
14. Найдите длину вектора
15. Найдите координаты вектора противоположного вектору
16. Даны векторы . Вычислите
17. Найдите косинус угла между векторами и

Проверочная работа по теме: « Координаты и векторы »

1. Дан вектор . Напишите координаты вектора
2. Упростите выражение:
3. Упростите выражение:
4. Упростите выражение:
5. Найдите координаты вектора , если
6. Даны векторы , найдите
7. Даны векторы , найдите
8. О начало координат, F (3;-1,5). Найдите координаты вектора
9. Дан вектор , найдите длину
10. Даны векторы , найдите координаты вектора
11. Найдите скалярное произведение векторов и
12. Найдите скалярное произведение векторов и
13. Найдите скалярное произведение векторов и
14. Найдите длину вектора
15. Найдите координаты вектора противоположного вектору
16. Даны векторы . Вычислите
17. Найдите косинус угла между векторами и

Наименование изученного вопроса учебного занятия

Контрольное задание по изученному вопросу

Использование координаты и векторов при решении математических и прикладных задач

Вычислите площадь параллелограмма, построенного на векторах , если

Видео:Скалярное произведение векторов через координаты. 9 класс.Скачать

Применение векторов к решению задач

Вы будете перенаправлены на Автор24

Видео:Выразить векторы. Разложить векторы. Задачи по рисункам. ГеометрияСкачать

Сущность векторного метода для решения геометрических задач

Векторный метод решения задач основан на решении задач с использованием аппарата векторной алгебры.

Применение векторной алгебры к решению геометрических задач основано на следующих основных утверждениях.

Утверждение 1 (Необходимое и достаточное условие коллинеарности векторов): Два ненулевых вектора $overrightarrow$ и $overrightarrow$ коллинеарны тогда и только тогда, когда существует действительное число $kne 0$, такое, что удовлетворяется следующее равенство

Утверждение 3: Любой вектор $overrightarrow$ в трехмерном пространстве можно разложить по трем некомпланарным векторам $overrightarrow$, $overrightarrow$ и $overrightarrow$:

При решении задач векторным методом также применяются такие понятия, как сложение, вычитание векторов, умножение вектора на число, а также понятие скалярного произведения векторов.

Видео:Нахождение координат вектора. Практическая часть. 9 класс.Скачать

Общая схема для решения геометрических задач векторным методом

При решении геометрических задач векторным методом рекомендуется пользоваться следующей схемой:

Провести анализ условия задачи:

а) Выяснить в какой системе координат (двумерной или трехмерной) рассматривается данная задача;

б) Записать, что нам дано, что нужно найти или доказать, а также построить чертеж по условию задачи.

Перевести условие задачи и требования к векторному виду.

Составить векторные соотношения, соответствующие тому, что дано в задаче и привести их к векторным соотношениям, соответствующим требованиям задачи.

Перевести полученный результат на геометрический язык.

Видео:Формулы векторов через координаты. Практическая часть. 9 класс.Скачать

Примеры типов задач, которые решаются векторным методом

Приведем теперь примеры классических задач, решаемых с помощью векторного метода (Не приводя их решений).

Задачи на доказательство параллельности.

Задачи на нахождение отношений, в котором точка делит отрезок.

Задачи на доказательство принадлежности трех точек одной прямой.

Задачи на доказательство принадлежности четырех точек одной плоскости.

Задачи на доказательство перпендикулярности.

Задачи на вычисление длины отрезка.

Задачи на нахождение величины угла.

Задачи на вычисление площадей и объемов геометрических фигур.

Готовые работы на аналогичную тему

Видео:11 класс, 1 урок, Прямоугольная система координат в пространствеСкачать

Примеры задач на применение векторного метода

Далее рассмотрим ряд задач, которые решаются с помощью векторного метода.

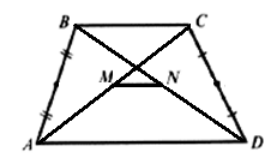
Доказать, что линия, соединяющая середины диагоналей произвольной трапеции параллельна основаниям этой трапеции и равна их полуразности.

Доказательство.

Пусть нам дана трапеция $ABCD.$ $MN$ — отрезок, соединяющий середины диагоналей данной трапеции (рис. 1).

Докажем, что $MN=frac$ и $MN||AD$

Рассмотрим вектор $overrightarrow$. Используя правило многоугольника для сложения векторов, с одной стороны, получим

С другой стороны

Сложим два последних равенства:

Так как $MN$ — отрезок, соединяющий середины диагоналей, то

Так как $overrightarrow и overrightarrow$ сонаправлены, то $overrightarrow||overrightarrow$.

Из этого получаем, что $MN=frac$ и $MN||AD$

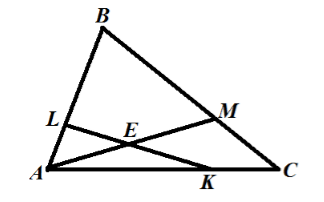
На сторонах треугольника $ABC$ взяты точки $L, M, K$, так что $left|BLright|=3left|ALright|, left|BMright|=2left|CMright|, left|AKright|=2|CK|$. Найти, в каком отношении прямая $KL$ делит отрезок $AM$.

Решение.

Обозначим через точку $E$ — точку пересечения отрезка $AM$ с прямой $KL$(рис. 2).

Введем, для удобства, следующие обозначения: $overrightarrow=overrightarrow, overrightarrow=overrightarrow$, $overrightarrow=xoverrightarrow,$ $overrightarrow=yoverrightarrow$

Воспользуемся далее правилом треугольника для сложения векторов. С одной стороны получим

С другой стороны

Ответ: $3:4.$

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 01 04 2021

📽️ Видео

КООРДИНАТЫ ВЕКТОРА В ПРОСТРАНСТВЕ решение задачСкачать

Классическая теория поля. Занятие 1. Сапонов П. А. Арсеев П. И.Скачать

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Математика без Ху!ни. Смешанное произведение векторовСкачать

Решение задач с помощью координат и векторовСкачать

Как выражать вектор? Как решать задачу с вектором? | TutorOnlineСкачать

СКАЛЯРНОЕ УМНОЖЕНИЕ ВЕКТОРОВ ЧАСТЬ I #математика #егэ #огэ #формулы #профильныйегэ #векторыСкачать

18+ Математика без Ху!ни. Векторное произведение.Скачать

Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать

Координаты вектора в пространстве. 11 класс.Скачать

ВЕКТОРЫ 9 класс С НУЛЯ | Математика ОГЭ 2023 | УмскулСкачать