Как найти сторону окружности если известен радиус и сторона

Видео:Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

Определение стороны окружности

Сторона окружности — это длина дуги окружности.

Длина дуги численно равна стороне
окружности, поэтому более распространено
понятие дуги окружности.

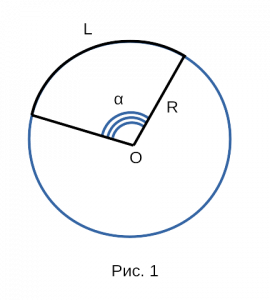
На рисунке 1, изображена окружность,
обладающая следующими величинами:

• O — точка, являющаяся
  центром окружности;
• R — радиус
  окружности;
• α — центральный
  угол окружности;
• L — сторона
  окружности;

Длину стороны L, окружности,
с центром в точке O, можно
найти следующим образом:

Ⅰ. Умножить радиус окружности на π,
получившееся разделить на 180 градусов.
Ⅱ. Полученный результат умножить на угол.

Также, все это можно сделать, зная одну из
известных формул стороны окружности:

Видео:№706. Найдите сторону равностороннего треугольника, если радиус описанной около него окружностиСкачать

Формулы стороны окружности

Ⅰ. Через диаметр и центральный угол

Сторону окружности L, можно найти, разделив
произведение половины диаметра и π на 180 градусов.
Затем умножить полученное значение на угол.

Ⅱ. Через площадь и центральный угол

Эта формула, примечательна тем, что
для нахождения длины, не обязательно
знать радиус — главное знать площадь.

Ⅲ. Через периметр и центральный угол

Самая краткая запись формулы
стороны окружности.

Видео:КАК НАЙТИ ДЛИНУ ОКРУЖНОСТИ, ЕСЛИ ИЗВЕСТЕН ДИАМЕТР ИЛИ РАДИУС? Примеры | МАТЕМАТИКА 6 классСкачать

Пример решения задач по теме сторона окружности

Возьмем для удобства π равное 3.14.

Ⅰ.
Дано: Диаметр равен 6, центральный равен 180.
Найти: Длина стороны окружности — ?

Решение:

( L = frac<frac cdot pi> cdot 180 = frac cdot 180 = 3pi = 9.42 )

Ⅱ.
Дано: Периметр равен 100, центральный угол равен 60.
Найти: Длина стороны окружности — ?

Решение:

( L = frac cdot 60 = 0.55 cdot 60 = 33 )

Видео:КАК НАЙТИ РАДИУС КРУГА (ОКРУЖНОСТИ), ЕСЛИ ИЗВЕСТНА ДЛИНА ОКРУЖНОСТИ? Примеры | МАТЕМАТИКА 6 классСкачать

Как найти сторону окружности если известен радиус

Видео:Задача 6 №27916 ЕГЭ по математике. Урок 133Скачать

Сторона окружности

Видео:Длина окружности. Математика 6 класс.Скачать

Определение стороны окружности

Сторона окружности — это длина дуги окружности.

Длина дуги численно равна стороне
окружности, поэтому более распространено
понятие дуги окружности.

На рисунке 1, изображена окружность,
обладающая следующими величинами:

• O — точка, являющаяся
  центром окружности;
• R — радиус
  окружности;
• α — центральный
  угол окружности;
• L — сторона
  окружности;

Длину стороны L, окружности,
с центром в точке O, можно
найти следующим образом:

Ⅰ. Умножить радиус окружности на π,
получившееся разделить на 180 градусов.
Ⅱ. Полученный результат умножить на угол.

Также, все это можно сделать, зная одну из
известных формул стороны окружности:

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Формулы стороны окружности

Ⅰ. Через диаметр и центральный угол

Сторону окружности L, можно найти, разделив
произведение половины диаметра и π на 180 градусов.
Затем умножить полученное значение на угол.

Ⅱ. Через площадь и центральный угол

Эта формула, примечательна тем, что
для нахождения длины, не обязательно
знать радиус — главное знать площадь.

Ⅲ. Через периметр и центральный угол

Самая краткая запись формулы
стороны окружности.

Видео:ЕГЭ 6 номер. Нахождение стороны правильного треугольника по радиусу вписанной окружности.Скачать

Пример решения задач по теме сторона окружности

Возьмем для удобства π равное 3.14.

Ⅰ.
Дано: Диаметр равен 6, центральный равен 180.
Найти: Длина стороны окружности — ?

Решение:

( L = frac cdot pi> cdot 180 = frac cdot 180 = 3pi = 9.42 )

Ⅱ.
Дано: Периметр равен 100, центральный угол равен 60.
Найти: Длина стороны окружности — ?

Решение:

( L = frac cdot 60 = 0.55 cdot 60 = 33 )

Видео:Как найти сторону квадрата через радиус?Скачать

Калькулятор расчета стороны правильного многоугольника через радиусы окружностей

В публикации представлены онлайн-калькуляторы и формулы для расчета длины стороны правильного многоугольника через радиус вписанной или описанной окружности.

Видео:✓ Как найти второй радиус? | Ботай со мной #105 | Борис ТрушинСкачать

Расчет длины стороны

Инструкция по использованию: введите радиус вписанной (r) или описанной (R) окружности, укажите количество вершин правильного многоугольника (n), затем нажмите кнопку “Рассчитать”. В результате будет вычислена длина стороны фигуры (a).

Видео:Длина окружности. Площадь круга - математика 6 классСкачать

Как найти радиус окружности

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Видео:КАК НАЙТИ ДИАМЕТР ОКРУЖНОСТИ, ЕСЛИ ИЗВЕСТНА ДЛИНА ОКРУЖНОСТИ? Примеры | МАТЕМАТИКА 6 классСкачать

Основные понятия

Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.

Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости. Если говорить проще, то это замкнутая линия, как, например, обруч и кольцо.

Круг — множество точек на плоскости, которые удалены от центра на расстоянии равном радиусу. Иначе говоря, плоская фигура, ограниченная окружностью, как мяч и блюдце.

Радиус — это отрезок, который соединяет центр окружности и любую точку на ней. Общепринятое обозначение радиуса — латинская буква R.

Возможно тебе интересно узнать — как найти длину окружности?

Видео:Окружность. Как найти Радиус и ДиаметрСкачать

Формула радиуса окружности

Определить способ вычисления проще, отталкиваясь от исходных данных. Далее рассмотрим девять формул разной степени сложности.

Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Если известна площадь круга

R = √ S : π, где S — площадь круга, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Если известна длина

R = P : 2 * π, где P — длина (периметр круга).

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).

Видео:Известна биссектриса равностороннего треугольника. Найти сторону этого треугольника. ОГЭ №16Скачать

Если известен диаметр окружности

R = D : 2, где D — диаметр.

Диаметр — отрезок, который соединяет две точки окружности и проходит через центр. Радиус всегда равен половине диаметра.

Видео:Найдите сторону треугольника, если другие его стороны равны 1 и 5Скачать

Если известна диагональ вписанного прямоугольника

R = d : 2, где d — диагональ.

Диагональ вписанного прямоугольник делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Если диагональ неизвестна, теорема Пифагора поможет её вычислить:

d = √ a 2 + b 2 , где a, b — стороны вписанного прямоугольника.

Видео:Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

Если известна сторона описанного квадрата

R = a : 2, где a — сторона.

Сторона описанного квадрата равна диаметру окружности.

Видео:Теорема Пифагора для чайников)))Скачать

Если известны стороны и площадь вписанного треугольника

R = (a * b * c) : (4 * S), где a, b, с — стороны, S — площадь треугольника.

Видео:Найдите сторону треугольника на рисункеСкачать

Если известна площадь и полупериметр описанного треугольника

R = S : p, где S — площадь треугольника, p — полупериметр треугольника.

Полупериметр треугольника — это сумма длин всех его сторон, деленная на два.

Если известна площадь сектора и его центральный угол

R = √ (360° * S) : (π * α), где S — площадь сектора круга, α — центральный угол.

Площадь сектора круга — это часть S всей фигуры, ограниченной окружностью с радиусом.

Если известна сторона вписанного правильного многоугольника

R = a : (2 * sin (180 : N)), где a — сторона правильного многоугольника, N — количество сторон.

В правильном многоугольнике все стороны равны.

Скачать онлайн таблицу

У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.

Треугольник. Соотношения между сторонами треугольника и радиусами вписанного и описанного кругов.

По двум сторонам a и b треугольника ABC и радиусу R описанного круга вычислить третью сторону x треугольника.

Применяя к этому четырехугольнику теорему Птоломея будем иметь:

откуда легко найдем x .

Задача будет иметь другое решение, если предположим, что стороны a и b лежат по одну сторону от центра. Применяя к этому случаю теорему Птоломея, мы получим следующее уравнение:

Теорема.

Произведение двух сторон треугольника равно:

1. произведению диаметра описанного круга на высоту, проведенную к третьей стороне.

2. квадрату биссектрисы угла, заключенного между этими сторонами, сложенному с произведением отрезков третьей стороны.

1.Обозначим стороны треугольника ABC через a, b и с, высоту, опущенную на сторону a через h_a , а радиус описанного круга через R.Проведем диаметр AD и соединим D с B.

Треугольники ABD и AEC подобны, потому что углы B и E прямые и D= С , как углы вписанные, опирающиеся на одну и ту же дугу.

Из этой формулы легко определить величину радиуса R описанного круга.

По первой теореме мы имеем: bс = 2Rh_a , где b и с есть две стороны треугольника, h_a — высота, опущенная на третью сторону треугольника, и R — радиус описанного круга.

Из этого равенства выводим:

Исключим из этой формулы высоту h_a: для этого умножим числитель и знаменатель дроби на a. Тогда, заменив произведение h_a a удвоенной площадью треугольника (которую обозначим S), получим:

,

Чтобы найти радиус r внутреннего вписанного круга рассмотрим треугольник АВС со вписанной в него окружностью. Отметим центр вписанной окружности и примем во внимание, что прямые OA, OB и OС разделяют данный треугольник на три других треугольника, у которых основаниями служат стороны данного треугольника, а высотой — радиус r.

Поэтому: S=1/2ar + 1/2br + 1/2cr = r ½ (a+b+c) = rp.