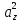Основы линейной алгебры для тех, кого это миновало в универе.
Вы наверняка слышали много историй о программистах, которые учились в технических вузах, изучали высшую математику и теперь пользуются этими знаниями в программировании. И если кого-то это не коснулось, может быть ощущение, что он пропустил в жизни что-то важное.
Будем это исправлять. Попробуем разобрать некоторые базовые понятия из математики за пределами школьной программы. И заодно покажем, как оно связано с программированием и для каких задач полезно.
⚠️ Математики, помогайте. Мы тут многое упростили, поэтому будем рады увидеть ваши уточнения и замечания в комментариях.
- Линейная алгебра
- Что такое вектор
- Как записывать
- Скаляр
- Как изображать
- И зачем нам это всё
- Что дальше
- Применение векторов в повседневной жизни
- Просмотр содержимого документа «Применение векторов в повседневной жизни»
- Творческая работа «Применение векторов»
- Просмотр содержимого документа «РАбота Вектор»
- 🎦 Видео
Видео:Зачем нужен ВЕКТОР. Объяснение смыслаСкачать

Линейная алгебра
Есть математика: она изучает абстрактные объекты и их взаимосвязи. Благодаря математике мы знаем, что если сложить два объекта с ещё двумя такими же объектами, то получится четыре объекта. И неважно, что это были за объекты: яблоки, козы или ракеты. Математика берёт наш вещественный мир и изучает его более абстрактные свойства.
Внутри математики есть алгебра: если совсем примитивно, то в алгебре мы вместо чисел начинаем подставлять буквы и изучать ещё более абстрактные свойства объектов.
Например, мы знаем, что если a + b = c , то a = c − b . Мы не знаем, что стоит на местах a, b или c, но для нас это такой абстрактный закон, который подтверждается практикой.
Внутри алгебры есть линейная алгебра — она изучает векторы, векторные пространства и другие абстрактные понятия, которые в целом относятся к некой упорядоченной информации. Например, координаты ракеты в космосе, биржевые котировки, расположение пикселей в изображении — всё это примеры упорядоченной информации, которую можно описывать векторами. И вот их изучает линейная алгебра.
В программировании линейная алгебра нужна в дата-сайенс, где из упорядоченной информации создаются алгоритмы машинного обучения.
Если представить линейную алгебру в виде дома, то вектор — это кирпич, из которого всё состоит. Сегодня разберёмся, что такое вектор и как его понимать.
Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Что такое вектор
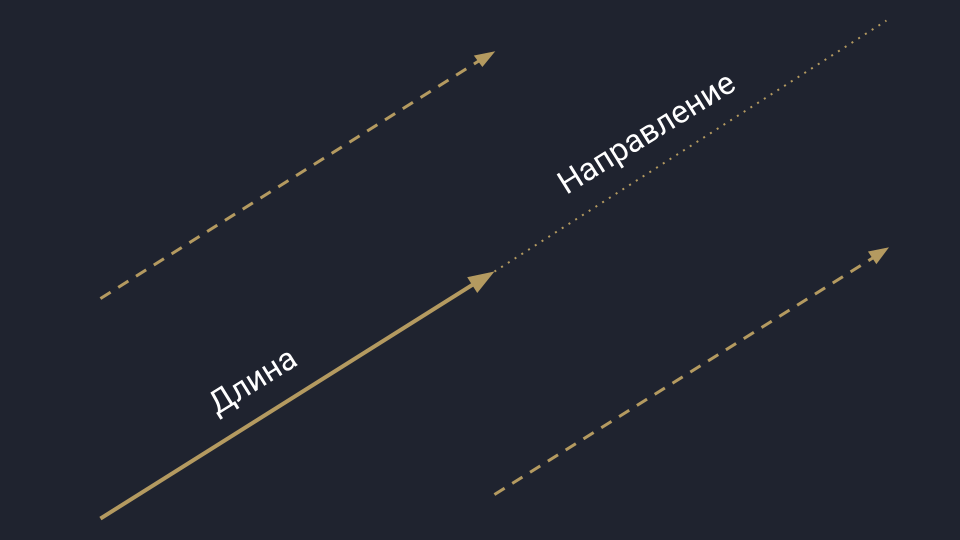
Вы наверняка помните вектор из школьной программы — это такая стрелочка. Она направлена в пространство и измеряется двумя параметрами: длиной и направлением. Пока длина и направление не меняются, вектор может перемещаться в пространстве.
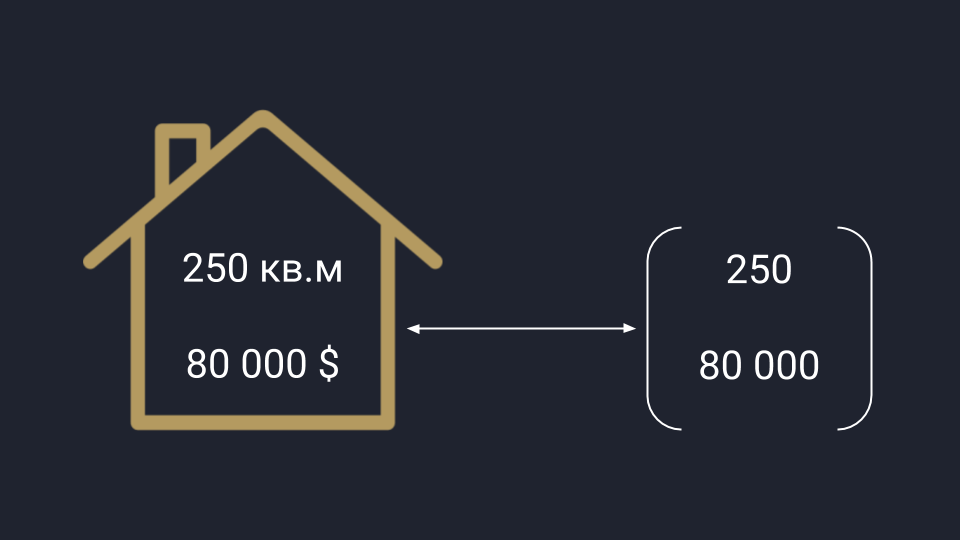
У аналитиков вектор представляется в виде упорядоченного списка чисел: это может быть любая информация, которую можно измерить и последовательно записать. Для примера возьмём рынок недвижимости, который нужно проанализировать по площади и цене домов — получаем вектор, где первая цифра отвечает за площадь, а вторая — за цену. Аналогично можно сортировать любые данные.
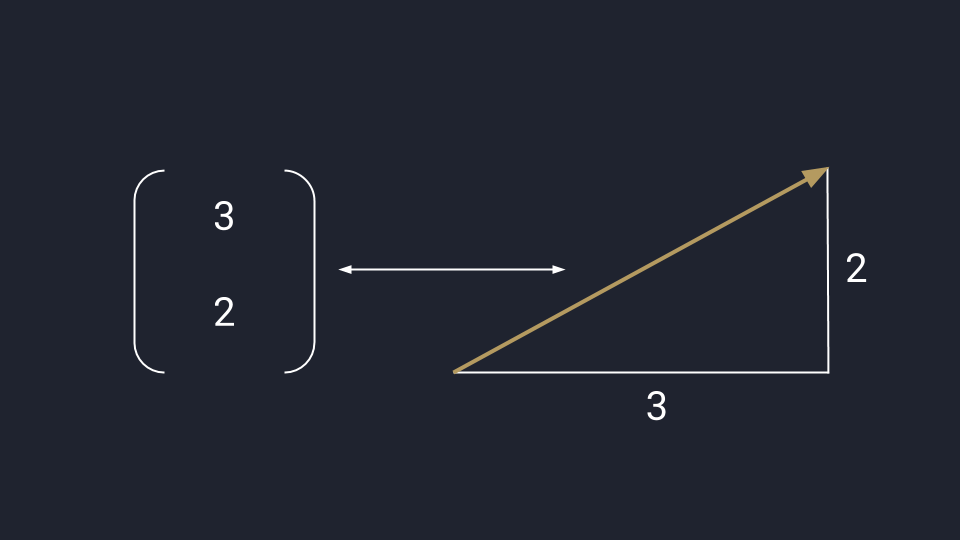
Математики обобщают оба подхода и считают вектор одновременно стрелкой и числом — это связанные понятия, перетекающие друг в друга в зависимости от задачи. В одних случаях удобней считать, а в других — показать всё графически. В обоих случаях перед нами вектор.
В дата-сайенс используется математическое представление вектора — программист может обработать данные и визуализировать результат. В отличие от физического представления, стрелки векторов в математике привязаны к системе координат Х и У — они не блуждают в пространстве, а исходят из нулевой точки.
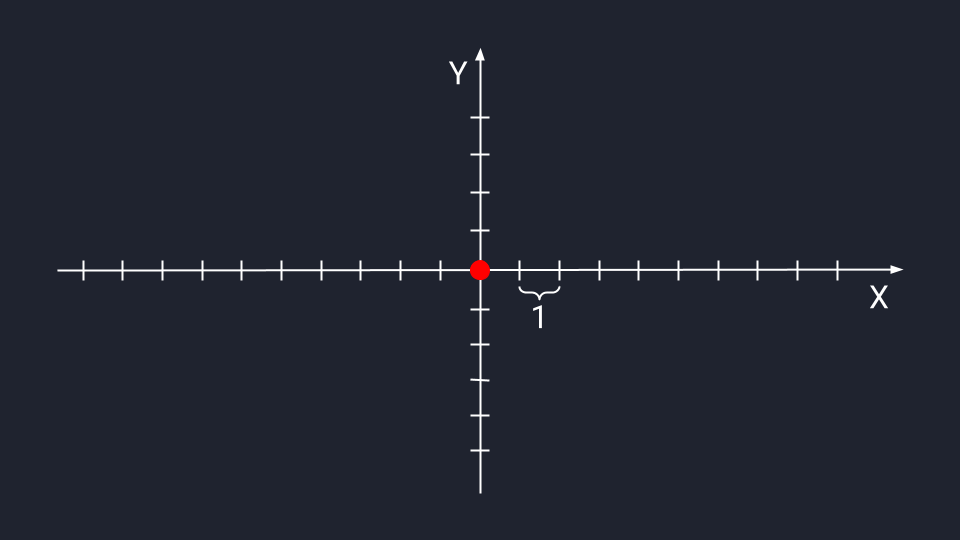
👉 Получается, вектор – это такой способ записывать, хранить и обрабатывать не одно число, а какое-то организованное множество чисел. Благодаря векторам мы можем представить это множество как единый объект и изучать его взаимодействие с другими объектами.
Например, можно взять много векторов с ценами на недвижимость, как-то их проанализировать, усреднить и обучить на них алгоритм. Без векторов это были бы просто «рассыпанные» данные, а с векторами — порядок.
Видео:Все о векторах за 60 минут | Математика ОГЭ | Молодой РепетиторСкачать

Как записывать
Вектор можно записать в строку или в столбец. Для строчной записи вектор обозначают одной буквой, ставят над ней черту, открывают круглые скобки и через запятую записывают координаты вектора. Для записи в столбец координаты вектора нужно взять в круглые или квадратные скобки — допустим любой вариант.
Строгий порядок записи делает так, что каждый набор чисел создаёт только один вектор, а каждый вектор ассоциируется только с одним набором чисел. Это значит, что если у нас есть координаты вектора, то мы их не сможем перепутать.
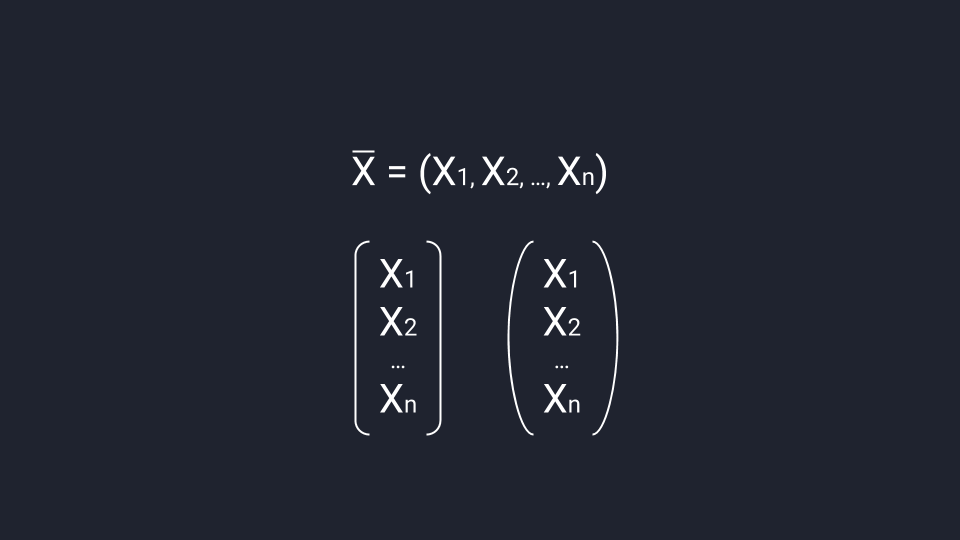
Скаляр
Помимо понятия вектора есть понятие скаляра. Скаляр — это просто одно число. Можно сказать, что скаляр — это вектор, который состоит из одной координаты.
Помните физику? Есть скалярные величины и есть векторные. Скалярные как бы описывают просто состояние, например, температуру. Векторные величины ещё и описывают направление.
Видео:✓ Что такое вектор? Чем отличается понятие "вектор" от понятия "направленный отрезок" | Борис ТрушинСкачать

Как изображать
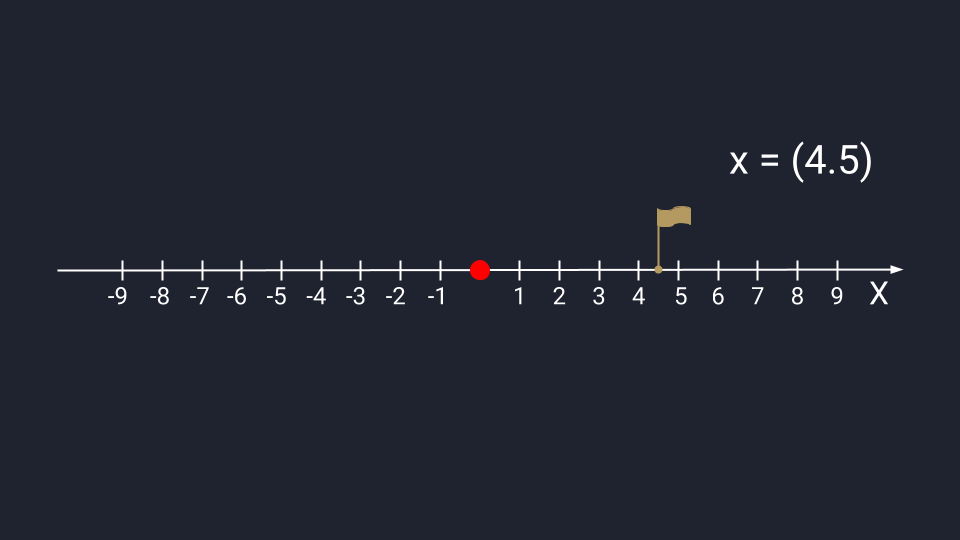
Вектор из одного числа (скаляр) отображается в виде точки на числовой прямой.
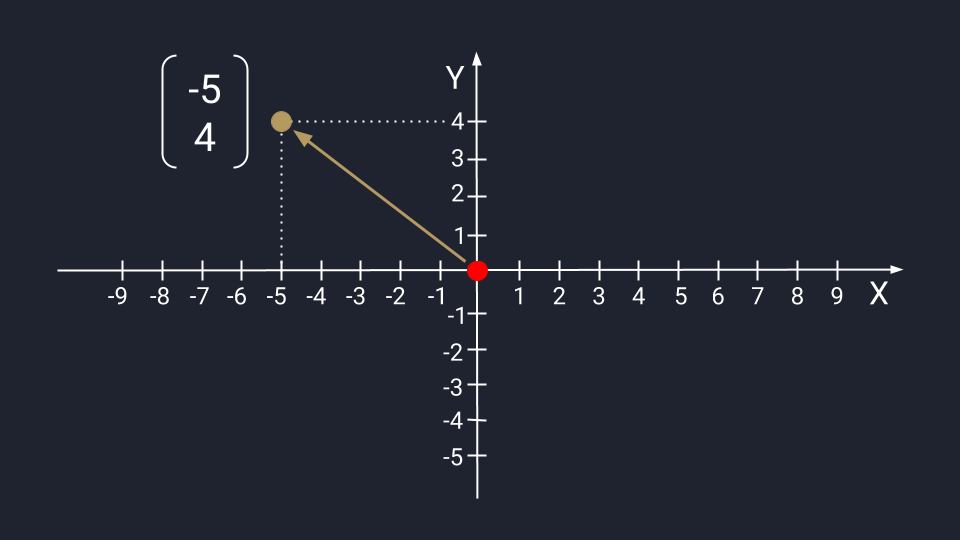
Вектор из двух чисел отображается в виде точки на плоскости осей Х и Y. Числа задают координаты вектора в пространстве — это такая инструкция, по которой нужно перемещаться от хвоста к стрелке вектора. Первое число показывает расстояние, которое нужно пройти вдоль оси Х; второе — расстояние по оси Y. Положительные числа на оси Х обозначают движение вправо; отрицательные — влево. Положительные числа на оси Y — идём вверх; отрицательные — вниз.
Представим вектор с числами −5 и 4. Для поиска нужной точки нам необходимо пройти влево пять шагов по оси Х, а затем подняться на четыре этажа по оси Y.
Вектор из трёх чисел отображается в виде точки на плоскости осей Х, Y и Z. Ось Z проводится перпендикулярно осям Х и У — это трёхмерное измерение, где вектор с упорядоченным триплетом чисел: первые два числа указывают на движение по осям Х и У, третье — куда нужно двигаться вдоль оси Z. Каждый триплет создаёт уникальный вектор в пространстве, а у каждого вектора есть только один триплет.
Если вектор состоит из четырёх и более чисел, то в теории он строится по похожему принципу: вы берёте координаты, строите N-мерное пространство и находите нужную точку. Это сложно представить и для обучения не понадобится.
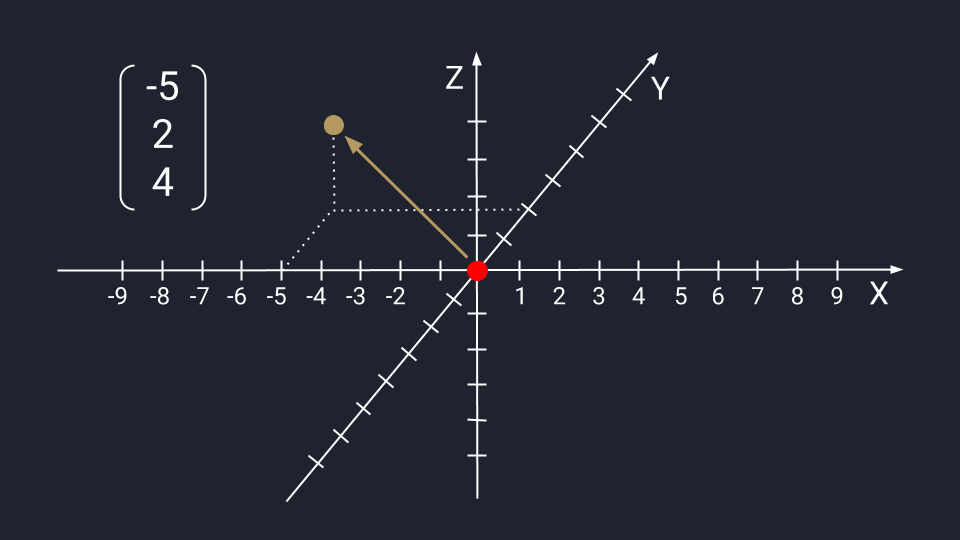
Помните, что все эти записи и изображения с точки зрения алгебры не имеют отношения к нашему реальному трёхмерному пространству. Вектор — это просто какое-то количество абстрактных чисел, собранных в строгом порядке. Вектору неважно, сколько там чисел и как их изображают люди. Мы же их изображаем просто для наглядности и удобства.
Например, в векторе спокойно может быть 99 координат. Для его изображения нам понадобилось бы 99 измерений, что очень проблематично на бумаге. Но с точки зрения вектора это не проблема: перемножать и складывать векторы из двух координат можно так же, как и векторы из 9999999 координат, принципы те же.
Видео:СКАЛЯРНОЕ УМНОЖЕНИЕ ВЕКТОРОВ ЧАСТЬ I #математика #егэ #огэ #формулы #профильныйегэ #векторыСкачать

И зачем нам это всё
Вектор — это «кирпичик», из которого строится дата-сайенс и машинное обучение. Например:
- На основании векторов получаются матрицы. Если вектор — это как бы линия, то матрица — это как бы плоскость или таблица.
- Машинное обучение в своей основе — это перемножение матриц. У тебя есть матрица с данными, которые машина знает сейчас; и тебе нужно эту матрицу «дообучить». Ты умножаешь существующую матрицу на какую-то другую матрицу и получаешь новую матрицу. Делаешь так много раз по определённым законам, и у тебя обученная модель, которую на бытовом языке называют искусственным интеллектом.
Кроме того, векторы используются в компьютерной графике, работе со звуком, инженерном и просто любом вычислительном софте.
И давайте помнить, что вектор — это не какая-то сложная абстрактная штука, а просто сумка, в которой лежат числа в определённом порядке. То, что мы называем это вектором, — просто нюанс терминологии.
Видео:Что такое вектора? | Сущность Линейной Алгебры, глава 1Скачать

Что дальше
В следующий раз разберём операции с векторами. Пока мы готовим материал — рекомендуем почитать интервью с Анастасией Никулиной. Анастасия ведёт ютуб-канал по дата-сайнс и работает сеньором дата-сайентистом в Росбанке.
Видео:ПРОСТОЙ СПОСОБ, как запомнить Векторы за 10 минут! (вы будете в шоке)Скачать

Применение векторов в повседневной жизни
С понятием вектора мы встречаемся чаще,чем сами подозреваем. В данной работе я постаралась максимально изучить, в каких же сферах мы взаимодействуем с ним.
Просмотр содержимого документа
«Применение векторов в повседневной жизни»
С уверенностью можно сказать, что мало кто из людей задумывается о том, что векторы окружают нас повсюду и помогают нам в повседневной жизни. Рассмотрим ситуацию: парень назначил девушке свидание в двухстах метрах от своего дома. Найдут ли они друг друга? Конечно, нет, так как юноша забыл указать главное: направление, то есть по-научному – вектор. Далее, в процессе работы над данным проектом, я приведу ещё множество не менее интересных примеров векторов.
Вообще, я считаю, что математика – это интереснейшая наука, в познании которой нет границ. Я выбрала тему о векторах не случайно, меня очень заинтересовало то, что понятие «вектор» выходит далеко за рамки одной науки, а именно математики, и окружает нас практически везде. Таким образом, каждый человек должен знать, что такое вектор, поэтому, я думаю, что эта тема весьма актуальна. В психологии, биологии, экономике и многих других науках употребляют понятие «вектор». Подробнее об этом я расскажу позже.
Целями данного проекта являются приобретение навыков работы с векторами, умение видеть необычное в обычном, выработка внимательного отношения к окружающему миру.
История возникновения понятия вектор
Одним из фундаментальных понятий современной математики является вектор. Эволюция понятия вектора осуществлялась благодаря широкому использованию этого понятия в различных областях математики, механики, а так же в технике.
Вектор относительно новое математическое понятие. Сам термин «вектор» впервые появился в 1845 году у ирландского математика и астронома Уильяма Гамильтона (1805 – 1865) в работах по построению числовых систем, обобщающих комплексные числа. Гамильтону принадлежат и термин «скаляр», «скалярное произведение», «векторное произведение». Почти одновременно с ним исследования в том же направлении, но с другой точки зрения вёл немецкий математик Герман Грассман (1809 – 1877). Англичанин Уильям Клиффорд (1845 – 1879) сумел объединить два подхода в рамках общей теории, включающий в себя и обычное векторное исчисление. А окончательный вид оно приняло в трудах американского физика и математика Джозайи Уилларда Гиббса (1839 – 1903), который в 1901 году опубликовал обширный учебник по векторному анализу.
Конец прошлого и начало текущего столетия ознаменовались широким развитием векторного исчисления и его приложений. Были созданы векторная алгебра и векторный анализ, общая теория векторного пространства. Эти теории были использованы при построении специальной и общей теории относительности, которые играют исключительно важную роль в современной физике.
Понятие вектора возникает там, где приходится иметь дело с объектами, которые характеризуются величиной и направлением. Например, некоторые физические величины, такие, как сила, скорость, ускорение и др., характеризуются не только числовым значением, но и направлением. В связи с этим указанные физические величины удобно изображать направленными отрезками. В соответствии с требованиями новой программы по математике и физике понятие вектора стало одним из ведущих понятий школьного курса математики.[2]
Векторы в математике
Вектором называется направленный отрезок, который имеет начало и конец.[1]




Два вектора называются коллинеарными, если они лежат на параллельных прямых, либо на одной прямой. Два вектора называются сонаправленными, если они коллинеарны и направлены в одну сторону, противоположно направленными, если коллинеарны и направлены в разные стороны.
Операции над векторами




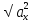
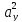
В координатном представлении вектор суммы получается суммированием соответствующих координат слагаемых:

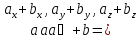

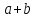


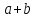
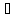

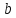
Это правило прямо и естественно обобщается для сложения любого количества векторов, переходя в правило ломаной:
Начало второго вектора совмещается с концом первого, начало третьего — с концом второго и так далее, сумма же 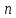
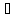

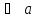
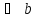
Правило параллелограмма особенно удобно, когда есть потребность изобразить вектор суммы сразу же приложенным к той же точке, к которой приложены оба слагаемых — то есть изобразить все три вектора имеющими общее начало.
Для получения разности в координатной форме надо вычесть соответствующие координаты векторов:




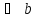
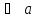
Умножение вектора на число


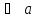

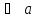
Скалярное произведение векторовСкалярное
Скалярным произведением называют число, которое получается при умножении вектора на вектор. Находится по формуле:

Скалярное произведение можно найти ещё через длину векторов и угол между ними. 
Применение векторов в смежных науках Векторы в физике Векторы — мощный инструмент математики и физики. На языке векторов формулируются основные законы механики и электродинамики. Чтобы понимать физику, нужно научиться работать с векторами. В физике, как и в математике, вектор – это величина, которая характеризуется своим численным значением и направлением. В физике встречается немало важных величин, являющихся векторами, например сила, положение, скорость, ускорение, вращающий момент, импульс, напряженность электрического и магнитного полей. Векторы в литературе Вспомним басню Ивана Андреевича Крылова о том, как «лебедь, рак да щука везти с поклажей воз взялись». Басня утверждает, что «воз и ныне там», другими словами, что равнодействующая всех сил приложенных к возу сил равна нулю. А сила, как известно, векторная величина. Векторы в химии
Нередко даже великими учеными высказывалась мысль, что химическая реакция является вектором. Вообще-то, под понятие «вектор» можно подвести любое явление. Вектором выражают действие или явление, имеющее четкую направленность в пространстве и в конкретных условиях, отражаемое его величиной. Направление вектора в пространстве определяется углами, образующимися между вектором и координатными осями, а длина (величина) вектора – координатами его начала и конца.
Однако утверждение, что химическая реакция является вектором, до сих пор было неточно. Тем не менее основой этого утверждения служит следующее правило: «Любой химической реакции отвечает симметричное уравнение прямой в пространстве с текущими координатами в виде количеств веществ (молей), масс или объемов».
Все прямые химических реакций проходят через начало координат. Любую прямую в пространстве нетрудно выразить векторами, но поскольку прямая химической реакции проходит через начало системы координат, то можно принять, что вектор прямой химической реакции находится на самой прямой и называется радиус-вектором. Начало этого вектора совпадает с началом системы координат. Таким образом, можно сделать вывод: любая химическая реакция характеризуется положением ее вектора в пространстве. Векторы в биологии
Вектором (в биологии) называется организм, переносящий паразита от одного организма-хозяина к другому. Например, вши переносят возбудителей сыпного тифа, крысы – чумы.
Вектор (в генетике) — молекула нуклеиновой кислоты, чаще всего ДНК, используемая в генетической инженерии для передачи генетического материала другой клетке.
Векторы в экономике
Одним из разделов высшей математики является линейная алгебра. Ее элементы широко применяются при решении разнообразных задач экономического характера. Среди них важное место занимает понятие вектора.
Вектор представляет собой упорядоченную последовательность чисел. Числа в векторе с учетом их расположения по номеру в последовательности называются компонентами вектора. Отметим, векторы можно рассматривать в качестве элементов любой природы, в том числе и экономической. Предположим, что некоторая текстильная фабрика должна выпустить в одну смену 30 комплектов постельного белья, 150 полотенец, 100 домашних халатов, тогда производственную программу данной фабрики можно представить в виде вектора, где всё, что должна выпустить фабрика – это трехмерный вектор.
Векторы в психологии
На сегодняшний день имеется огромное количество информационных источников для самопознания, направлений психологии и саморазвития. И не трудно заметить, что все больше обретает популярность такое необычное направление, как системно-векторная психология, в ней существует 8 векторов.
Векторы в повседневной жизни
Я обратила внимание, что векторы, помимо точных наук, встречаются мне каждый день. Так, например, во время прогулки в парке, я заметила, что ель, оказывается, можно рассматривать как пример вектора в пространстве: нижняя её часть – начало вектора, а верхушка дерева является концом вектора. А вывески с изображением вектора при посещении больших магазинов помогают нам быстро найти тот или иной отдел и сэкономить время.
Векторы в знаках дорожного движения
Каждый день, выходя из дома, мы становимся участниками дорожного движения в роли пешехода либо в роли водителя. В наше время практически каждая семья имеет машину, что, разумеется, не может не отразиться на безопасности всех участников дорожного движения. И, чтобы избежать казусов на дороге, стоит соблюдать все правила дорожного движения. Но не стоит забывать того, что в жизни всё взаимосвязано и, даже в простейших предписывающих знаках дорожного движения, мы видим указательные стрелки движения, в математике называемые – векторами. Эти стрелки (векторы) указывают нам направления движения, стороны движения, стороны объезда, и ещё многое другое. Всю эту информацию можно прочитать на знаках дорожного движения на обочинах дорог.
Базовое понятие «вектор», рассмотренное нами ещё на уроках математики в школе, является основой для изучения в разделах общей химии, общей биологии, физики и других наук. Я наблюдаю необходимость векторов в жизни, которые помогают найти нужный объект, сэкономить время, они выполняют предписывающую функцию в знаках дорожного движения.
Каждый человек постоянно сталкивается с векторами в повседневной жизни.
Векторы необходимы нам для изучения не только математики, но и других наук.
Видео:ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать

Творческая работа «Применение векторов»
Творческая работа практическоц направленности с презентацией
Просмотр содержимого документа
«РАбота Вектор»
Возникновение понятия «вектор»………………………….
Векторы в профессиях
С понятием вектор я познакомилась на уроках геометрии. Особого интереса она у меня не вызвала. Однако, практически сразу понятие «вектор» встретилось и на уроках физики. Тогда стало ясно, что вектор не сугубо математическое понятие, оно применяется и в других областях науки. Вектор — это направленный отрезок. А зачем они нужны? Встречаются ли они в жизни? Может, стоит присмотреться? Если вы начинаете утро с прогноза погоды, то слышали, к примеру: «Ветер северо-западный, скорость 18 метров в секунду». Нельзя не согласится,, имеет значение и направление ветра (откуда он дует), и модуль (то есть абсолютная величина) его скорости. Идем в школу: видим дорожные знаки, вроде этих:
Придя в школу или на работу, видим направляющие знаки:
Примеры направляющих знаков вы можете увидеть в Приложении 1. Видим, что векторы присутствуют в нашей жизни.
Актуальность изучения данной темы связано с многообразием сфер применения векторов: от искусства до сложных задач моделирования реальных процессов. Понятие вектора используется во многих приложениях математики, таких, как современная алгебра и геометрия, теория функций и теория вероятностей. Учебники по таким, на первый взгляд, далеким от математики предметам, как электротехника, радиотехника, теория антенн и др., очень широко используют векторы.
Я решила выяснить, в каких именно областях науки применяются векторы, насколько это понятие актуально в жизни.
Целью моей работы:
Рассмотреть векторы как математические модели реальных процессов.
Перед собой я поставила такие задачи:
Изучить литературу по данной теме;
Изучить понятие «вектор» в предметах естественно-научного цикла;
Узнать, как осуществляется моделирование с помощью векторов.
Установить, используется ли данное понятие в жизни;
Возникновение понятия «вектор»
Одним из основных понятий математики являются «вектор». Развитие этого понятия происходило благодаря широкому использованию его в различных областях математики, информатики, механики, а так же в технике.
Вектор – молодое математическое понятие. Этот термин впервые употребил ирландский математик Уильям Гамильтон в 1845 году в своих работах по построению числовых систем, обобщающих комплексные числа. Также он ввел термины «скаляр», «скалярное произведение», «векторное произведение». Исследования в этой области проводил ещё немецкий физик-математик Г.Грассман. Его идеи об абстрактных векторных пространствах привели к важному открытию – возможности рассматривать цветовые ощущения как трехмерные векторы. Это легло в основу современного учения о свете. Им были установлены законы сложения цветов.
Понятие «вектор» стало широко использоваться в математике в XIX веке, когда стал активно развиваться раздел математики «Комплексные числа». Векторы использовались для наглядного представления таких чисел. В школах эта тема изучается с 1963 года. Сейчас понятие вектора стало одним из ведущих понятий школьного курса математики.
Есть такое высказывание: «Карьера начинается в школе», поэтому я решила глубже изучить понятие «вектор», рассмотреть его значение в математическом моделировании и выяснить в каких профессиях применяется данное понятие.
Использование векторов в различных науках:
Векторы — мощный инструмент не только математики, но и физики. Понятие вектора возникает там, где приходится иметь дело с объектами, которые характеризуются величиной и направлением. Многие физические величины, такие, как сила, скорость, ускорение, характеризуются не только числовым значением, но и направлением. Эти величины очень удобно изображать в виде направленных отрезков. На языке векторов формулируются основные законы механики и электродинамики. Чтобы понимать физику, нужно научиться работать с векторами. Векторная алгебра является фундаментом, на котором построена классическая физика. С помощью векторов можно моделировать различные физические процессы. Например, некоторые физические поля (магнитное и электромагнитное, сила тяжести) рассматриваются как векторные поля. Такая модель позволяет применять к изучаемым понятиям удобные методы математических расчётов.
Векторные величины в физике: скорость, перемещение, ускорение, сила, импульс, напряженность электрического поля, магнитная индукция, момент силы. Для этих величин важно «сколько» и «куда».
Скорость изучается на уроках математики и на уроках физики, и при решении многих задач на скорость необходимо сделать рисунок, на котором направление движения показывается стрелками. Векторами удобно моделировать движение в одном направлении, в разных направлениях, движение по кругу, движение по воде. Составленная таким образом схема-модель поможет решить задачу.
Пример схем некоторых задач на движение:
Тело с большей скоростью догоняет тело с меньшей скоростью:
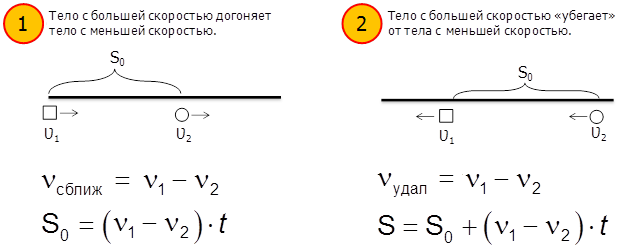
Движение в противоположные стороны:
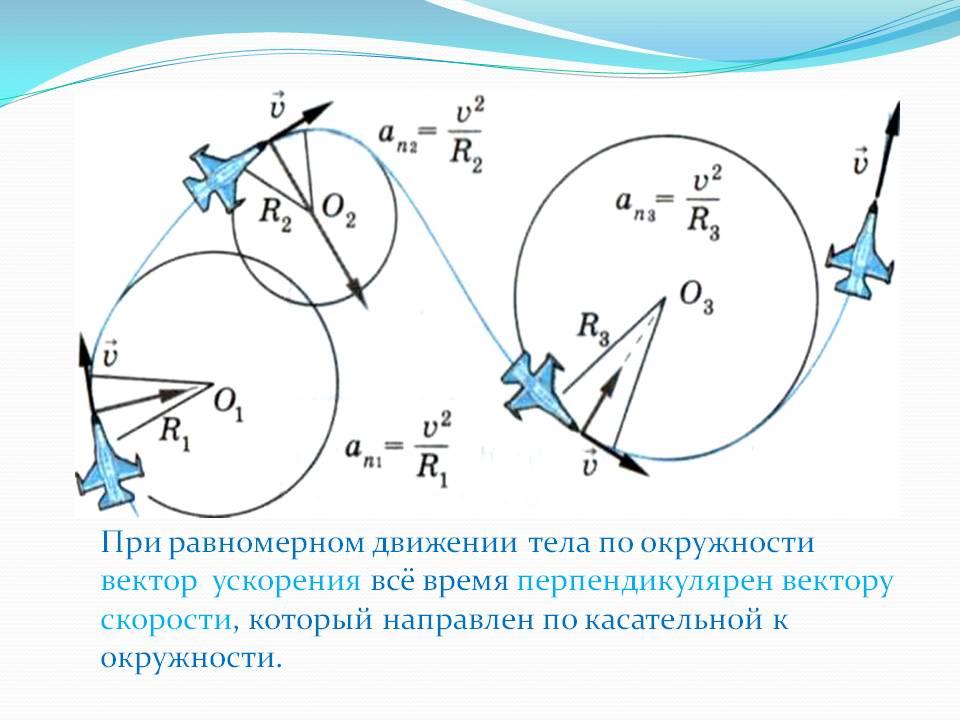
Равномерным движением по окружности называется такое движение, при котором скорость не меняется по модулю, а меняется лишь её направление. При этом вектор ускорения перпендикулярен вектору скорости. Вектор скорости направлен по касательной к окружности.
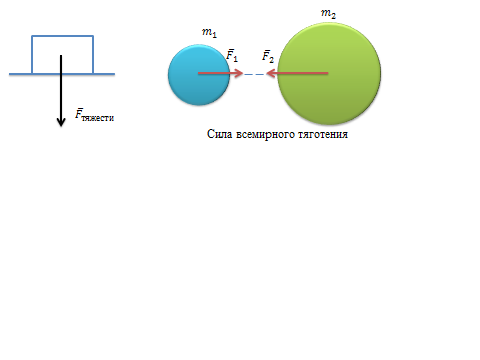
Еще одна физическая векторная величина, которую я хотела бы рассмотреть – это сила. Сила определяет меру интенсивности воздействия, которое оказывается на тело со стороны других тел или полей. Результат действия силы зависит от направления. На рисунке вы можете видеть модель направления силы тяжести и всемирного тяготения.
В физике можно найти ещё много примеров, где векторы применяются как средство моделирования физических процессов.
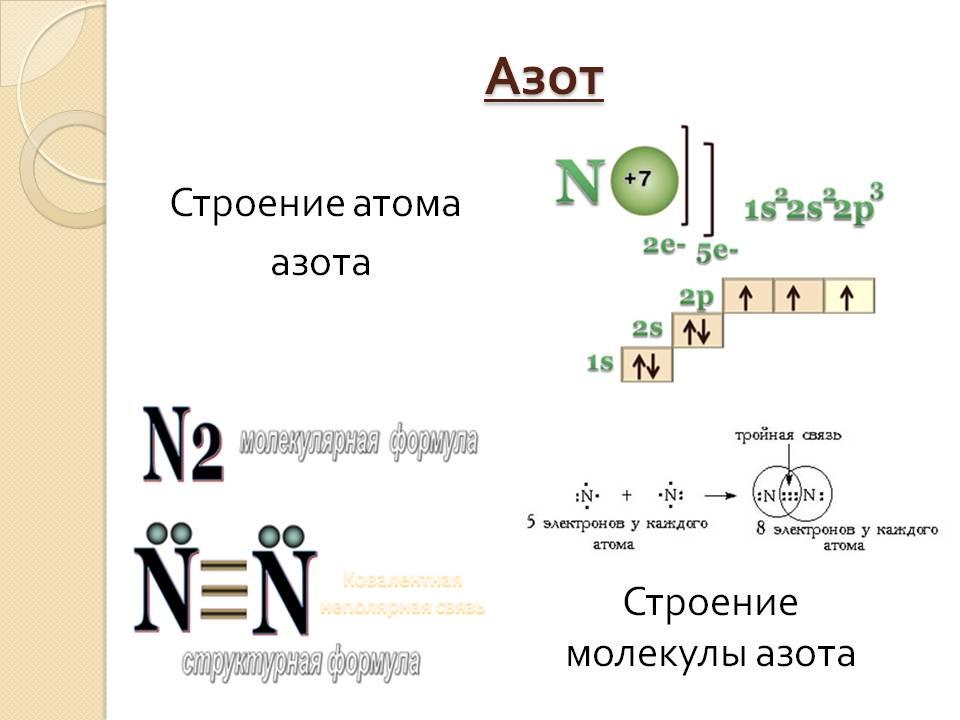
Также векторы помогают создавать математические модели некоторых химических процессов. Например, для того, чтобы показать строение атома используются всё те же векторы.
На схеме вы можете видеть строение атома азота:
На таких схемах стрелками изображается электрон, а направление соответствует направлению спина (собственного магнитного момента электрона). Операции над спинами производятся так же, как и операции над векторами, что позволяет трактовать химические процессы языком математики. Примером векторных частиц, имеющих спин служат: фотон, глюон, W- и Z-бозоны, векторные мезоны, ортопозитроний.
Химические реакции записываются с помощью уравнений, в записи которых используются векторы.
Пример, реакция обмена, взаимодействие хлорида кальция и нитрата серебра с образованием осадка хлорида серебра:
CaCl2( ж ) + 2AgNO3( ж ) 
Биология относится к наукам естественно-математического цикла. Часто для того, чтобы смоделировать тот или иной процесс, приходится использовать язык математики или переносить суть математических понятий на понятия биологические. Суть понятия «вектор» — это направленность. В биологии этим словом называют организм, который переносит паразита от одного организма к другому. Например, клещи являются переносчиками вируса, вызывающего энцефалит. В генетике вектором считается молекула нуклеиновой кислоты, которая используется для передачи генетического материала другой клетке. С помощью организмов векторов синтезируются различные лекарственные средства, в том числе и антибиотики, ферменты, необходимые человеку (инсулин).
В настоящее время создана векторная модель для доставки в клетки костного мозга гена, кодирующего гранулоцитарный колониестимулирующий фактор человека. Данный белок относится увеличивает продолжительность жизни клеток костного мозга, усиливает функциональную активность зрелых нейтрофилов. Созданный вектор представляет собой многослойную конструкцию. Эффективность описанной векторной модели была доказана опытным путем. При конструировании противовирусных вакцин немаловажное значение имеет создание специального вектора-носителя, обеспечивающего адресную доставку генов и их защиту от действия нуклеаз крови.
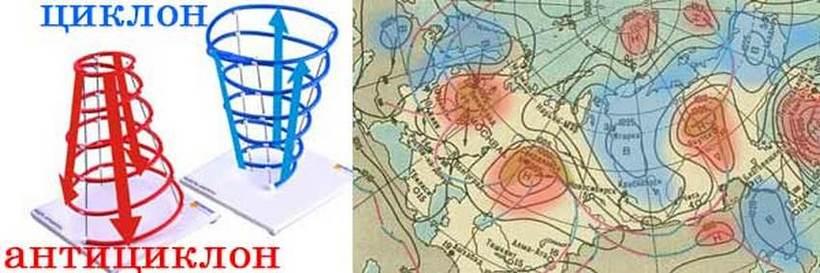
Оказывается, векторы, как отрезки, показывающие направление нашли своё отражение и в географии. Так, ветер – характеризуемый величиной и направлением, рассматривается как вектор. Распределение ветра исследуется в векторной форме. Таким образом, ветер (горизонтальное движение воздушных частиц относительно подстилающей поверхности) – векторная величина и описывается двумя параметрами – скоростью ( м/с) и направлением. Вектор – модель ветра. Аналогично, с помощью векторов показывают направление движения воздушных масс в циклонах и антициклонах.
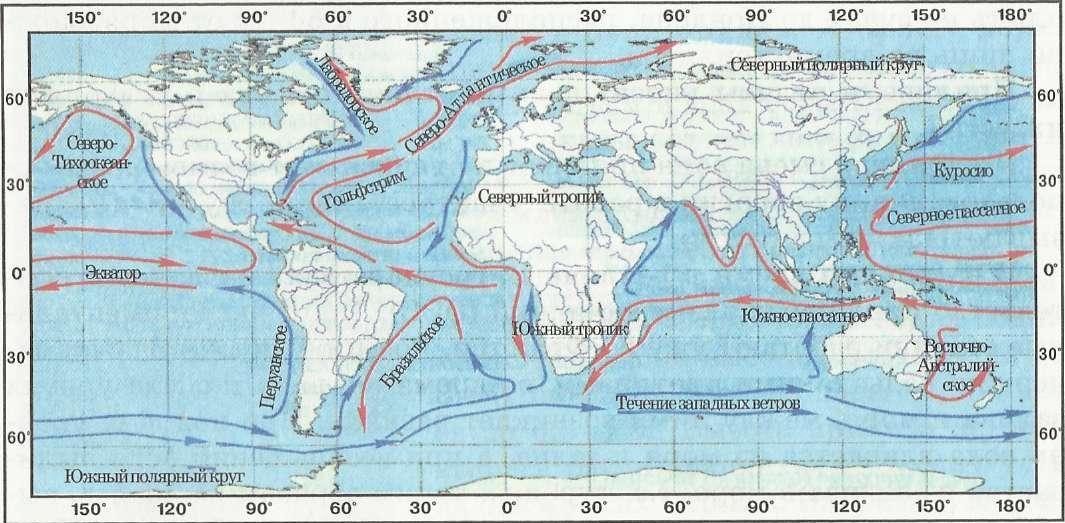
Вектор также служит моделью всевозможных течений. Горизонтальные перемещения водных масс в морях и океанах называются морскими течениями. К элементам, характеризующим течение, относятся направление и скорость. Значит, течение – векторная величина. С помощью векторов и действий над ними осуществляется учет приливно-отливных течений.
Течение реки, подводные течения океанов показывают с помощью векторов.
С помощью векторов составляют карты миграции птиц и животных.
Используя действия над векторами можно рассчитать пролетные пути перелетных птиц.
Векторы в профессиях.
Я выяснила, что векторы используются во многих науках для моделирования самых различных процессов и явлений. Значит, это понятие потребуется во всех технических профессиях, профессиях, связанных с компьютерном деле, в медицине, химии и т.д. Векторы нужны для освоения профессии строителя и архитектора, так как особое место вектору отводится в сопромате, ведь нагрузка на разные элементы конструкций является разложением вектора по базису векторов силы тяжести и других приложенных к конструкции сил. В самолетостроении, судостроении, автомобилестроении при конструировании транспорта также применяются векторы и их свойства.
В науке судовождение используются векторы и их свойства для определения кажущегося ветра во время движения судна. В штилевую погоду на судне, имеющего ход, всегда ощущается встречный ветер, равный скорости судна. Он имеет название курсовой ветер и имеет направление, противоположное движению судна. Таким образом, на движущемся судне наблюдается кажущийся ветер, вектор которого равен геометрической сумме истинного и курсового ветров. Для определения направления ветра используется способ построения векторного треугольника.
Векторы понадобятся и портному для правильного составления выкроек одежды.
Выполнив работу, я увидела, что векторы находят широкое применение в геометрии и в прикладных науках, где используются для представления величин, имеющих направление (силы, скорости и т. п.).
Вектор может служить моделью для любого явления, характеризующегося величиной и направлением. Так, в физике – это сила, ускорение, скорость; в химии – это изображения строения атома, изображения химических реакций; в биологии – это модель переноса вирусов, процессов клонирования и создания вакцин; в географии – это модель ветра, течения. Таким образом, векторное исчисление является универсальным инструментом, позволяющим создавать математические модели физических, химических и биологических процессов. Векторы широко используются в экономике и компьютерной графике, при построении вычислительных нейронных структур и всем известных популярных социальных сетей. Умение оперировать с объектами посредством векторного исчисления помогает находить удобные и наглядные пути решения сложных задач, поэтому хорошее знание этого раздела школьной математики необходимо каждому, чья будущая профессия связана с техникой, компьютерами, естественными науками, пространственным мышлением.
Башмаков М.А. Что такое вектор?-2-е изд., стер.- М.: Квант, 1976.-221с.
Выгодский М.Я. Справочник по элементарной математике.-3-е изд., стер. — М.: Наука, 1978.-186с.
Гусятников П.Б. Векторная алгебра в примерах и задачах.-2-е изд., стер.- М.: Высшая школа, 1985.-302с.
В.В. Элементарная математика. Повторительный курс.-3-е изд., стер.- М.: Наука,1976.-156с.
Коксетер Г.С. Новые встречи с геометрией.-2-е изд., стер. — М.: Наука,1978.-324с.
Погорелов А.В. Аналитическая геометрия.- 3-е изд., стер. — М.: Квант,1968.-235с.
🎦 Видео
ИСТОРИЯ VECTOR, КОТОРУЮ ВЫ НЕ ЗНАЛИ | ЛЕГЕНДАРНЫЕ ИГРЫ ДЕТСТВАСкачать

САМЫЕ Необычные Открытия Археологов, Которые Вас УдивятСкачать

Урок 3. Произведение векторов и загадочный угол между векторами. Высшая математика | TutorOnlineСкачать

Вектора. Что нужно знать про вектор, когда идешь на первый курс.Скачать

➡️ КАК ВЫЧИТАТЬ ВЕКТОРЫ?Скачать

РАЗБИРАЕМ ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ II 😊#shorts #математика #егэ #задачи #егэ2022 #огэ2022Скачать

Урок 8. Векторные величины. Действия над векторами.Скачать

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

ВЕКТОРЫ 9 класс С НУЛЯ | Математика ОГЭ 2023 | УмскулСкачать

А ТЫ УЖЕ РАЗОБРАЛСЯ С УМНОЖЕНИЕМ ВЕКТОРОВ? ЧАСТЬ II #математика #егэ #огэ #формулы #профильныйегэСкачать

Координаты вектора в пространстве. 11 класс.Скачать

Физика | Ликбез по векторамСкачать