Геометрия | 5 — 9 классы
Стороны прямоугольника равны 8 и 6 найдите радиус окружности описанной около этого прямоугольника.
5, по теореме пифагора найдем диагональ прямоугольника (гипотенузу)
8² + 6² = 64 + 36 = 100, √100 = 10 радиус окружности, описанной около прямоугольника, равен половине гипотенузы, 10÷2 = 5.
- Найдите радиус окружности описанной около прямоугольника две стороны которого равны 7 и корень из 95?
- Стороны прямоугольника равны 10 и 24?
- Около прямоугольника ABCD описана окружность, радиусом 6, 5см?
- Стороны прямоугольника равны 10 см и 24 см?
- Стороны прямоугольника равны 10 и 24?
- 1. найдите радиус окружности, описанной около прямоугольника, две стороны которого равны 27 и корень из 295 2?
- Стороны прямоугольника равны 10 и 24?
- Стороны прямоугольника = 8 и 6 найти радиус окружности описанной около этого прямоугольника?
- Около прямоугольника ABCD описана окружность, радиусом 5 см?
- Стороны прямоугольника равны 8 и 6?
- Как найти радиус окружности
- Основные понятия
- Формула радиуса окружности
- Если известна площадь круга
- Если известна длина
- Если известен диаметр окружности
- Если известна диагональ вписанного прямоугольника
- Если известна сторона описанного квадрата
- Если известны стороны и площадь вписанного треугольника
- Если известна площадь и полупериметр описанного треугольника
- Если известна площадь сектора и его центральный угол
- Если известна сторона вписанного правильного многоугольника
- Скачать онлайн таблицу
- Прямоугольник. Онлайн калькулятор
- Свойства прямоугольника
- Диагональ прямоугольника
- Окружность, описанная около прямоугольника
- Формула радиуса окружности описанной около прямоугольника
- Периметр прямоугольника
- Формулы сторон прямоугольника через его диагональ и периметр
- Признаки прямоугольника
Видео:Геометрия. ОГЭ по математике. Задание 16Скачать

Найдите радиус окружности описанной около прямоугольника две стороны которого равны 7 и корень из 95?
Найдите радиус окружности описанной около прямоугольника две стороны которого равны 7 и корень из 95.
Видео:Задача 6 №27934 ЕГЭ по математике. Урок 148Скачать

Стороны прямоугольника равны 10 и 24?
Стороны прямоугольника равны 10 и 24.
Найдите радиус окружности, описанной около этого прямоугольника.
Видео:Задача 6 №27921 ЕГЭ по математике. Урок 138Скачать

Около прямоугольника ABCD описана окружность, радиусом 6, 5см?
Около прямоугольника ABCD описана окружность, радиусом 6, 5см.
Найдите периметр прямоугольника, если одна из его сторон равна 5см.
Видео:Задача 6 №27923 ЕГЭ по математике. Урок 140Скачать

Стороны прямоугольника равны 10 см и 24 см?
Стороны прямоугольника равны 10 см и 24 см.
Вычислите Радиус описанной около прямоугольника окружности.
Видео:Шестнадцатое задание ОГЭ по математике (1) #огэ #огэ2023 #огэматематика #огэпоматематике #математикаСкачать

Стороны прямоугольника равны 10 и 24?
Стороны прямоугольника равны 10 и 24.
Найдите радиус окружности, описанной около это прямоугольника.
Видео:Задача 6 №27909 ЕГЭ по математике. Урок 129Скачать

1. найдите радиус окружности, описанной около прямоугольника, две стороны которого равны 27 и корень из 295 2?
1. найдите радиус окружности, описанной около прямоугольника, две стороны которого равны 27 и корень из 295 2.
Найдите диагональ прямоугольника вписанного в окружность радиус которой равен 2 корень из 2.
3. Найдите радиус окружности описанной около прямоугольника две стороны которого равны 11 и корень из 135.
Видео:Задача 6 №27932 ЕГЭ по математике. Урок 146Скачать

Стороны прямоугольника равны 10 и 24?
Стороны прямоугольника равны 10 и 24.
Найдите чему равен радиус описанной окружности около этого прямоугольника.
Видео:Задача 6 №27918 ЕГЭ по математике. Урок 135Скачать

Стороны прямоугольника = 8 и 6 найти радиус окружности описанной около этого прямоугольника?
Стороны прямоугольника = 8 и 6 найти радиус окружности описанной около этого прямоугольника.
Видео:2 круга 1 квадрат ➜ Задача от @AndyMath ➜ Найдите площадь квадрата на рисункеСкачать

Около прямоугольника ABCD описана окружность, радиусом 5 см?
Около прямоугольника ABCD описана окружность, радиусом 5 см.
Найдите периметр прямоугольника, если одна из его сторон равна 8 см.
Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Стороны прямоугольника равны 8 и 6?
Стороны прямоугольника равны 8 и 6.
Найдите радиус окружности, описанной возле этого прямоугольника.
Вы открыли страницу вопроса Стороны прямоугольника равны 8 и 6 найдите радиус окружности описанной около этого прямоугольника?. Он относится к категории Геометрия. Уровень сложности вопроса – для учащихся 5 — 9 классов. Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие ответы по интересующей теме. Чтобы получить наиболее развернутый ответ, можно просмотреть другие, похожие вопросы в категории Геометрия, воспользовавшись поисковой системой, или ознакомиться с ответами других пользователей. Для расширения границ поиска создайте новый вопрос, используя ключевые слова. Введите его в строку, нажав кнопку вверху.
1 задание Ответ 1, 3, 5 Карандашом можно отметить 1)отметить произвольную точку на данной прямой 3)отметить точку пересечения данных прямых 5)отметить произвольную точку на плоскости. 2 задание Я бы выбрала все варианты ответа 3 задание Ответ 1, 2, ..
Формула площади круга S : п * r ^ 2 Сторона квадрата вписанного в круг равна : Sqrt(r ^ 2 + r ^ 2) = Sqrt(2r ^ 2) = r * Sqrt(2) , Значит ребро вписанного куба равно : r * Sqrt(2), и соответственно и высота цилиндра будет равна : r * Sqrt(2) . Объем ..
Используй формулу средней линии трапеции.
H из корня равна 400 — 256 = 12h / 16 = x / 20x = (h * 20) / 16x = 12 * 20 / 16 = 15S = 20 * x / 2 = 20 * 15 / 2 = 150 см2Все / означают дробь.
Говорят, что они пересекаются.
Пересекаются эти окружности.
По условию задачи∠В = ∠С, АВ = СД∠А = ∠Д, значит по 2 признаку равенства треугольников ΔАВД = ΔАСД, значит и∠1 = ∠2.
1) Рассмотрим треугольник COA : 2) AC || DB.
Вот по моему так , Н1Н2СН3 — семеричная фигура относительно Н.
Найдём MN через тангенс. Tgα = OL / ML ⇒ ML = OL / tg30° ⇒ ML = / / 3 = 3 MN = 2ML ⇒ 2 * 3 = 6.
Видео:Найти радиус равнобедренного прямоугольного треугольника 3 задание проф. ЕГЭ по математикеСкачать

Как найти радиус окружности
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Видео:Задача 6 №27910 ЕГЭ по математике. Урок 130Скачать

Основные понятия
Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости. Если говорить проще, то это замкнутая линия, как, например, обруч и кольцо.
Круг — множество точек на плоскости, которые удалены от центра на расстоянии равном радиусу. Иначе говоря, плоская фигура, ограниченная окружностью, как мяч и блюдце.
Радиус — это отрезок, который соединяет центр окружности и любую точку на ней. Общепринятое обозначение радиуса — латинская буква R.
Возможно тебе интересно узнать — как найти длину окружности?
Видео:Задача№25 ОГЭ Точка M и N лежат на стороне АС. Найдите радиус окружности, если cos ВАС ...Скачать

Формула радиуса окружности
Определить способ вычисления проще, отталкиваясь от исходных данных. Далее рассмотрим девять формул разной степени сложности.
Видео:Задача 6 №27913 ЕГЭ по математике. Урок 131Скачать

Если известна площадь круга
R = √ S : π, где S — площадь круга, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.
Видео:Задание 3 ЕГЭ по математике. Урок 45Скачать
Если известна длина
R = P : 2 * π, где P — длина (периметр круга).
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).
Видео:Радиус окружности с центром в точке O равен 85 ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Если известен диаметр окружности
R = D : 2, где D — диаметр.
Диаметр — отрезок, который соединяет две точки окружности и проходит через центр. Радиус всегда равен половине диаметра.
Видео:ОГЭ 2020 задание 17Скачать

Если известна диагональ вписанного прямоугольника
R = d : 2, где d — диагональ.
Диагональ вписанного прямоугольник делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Если диагональ неизвестна, теорема Пифагора поможет её вычислить:
d = √ a 2 + b 2 , где a, b — стороны вписанного прямоугольника.
Видео:таблица умножения школаСкачать

Если известна сторона описанного квадрата
R = a : 2, где a — сторона.
Сторона описанного квадрата равна диаметру окружности.
Видео:Задание 3 ЕГЭ по математике. Урок 46Скачать

Если известны стороны и площадь вписанного треугольника
R = (a * b * c) : (4 * S), где a, b, с — стороны, S — площадь треугольника.
Видео:Задание 16 ОГЭ по математике. Две окружности одна описана около квадрата, другая вписана в него.Скачать

Если известна площадь и полупериметр описанного треугольника
R = S : p, где S — площадь треугольника, p — полупериметр треугольника.
Полупериметр треугольника — это сумма длин всех его сторон, деленная на два.
Если известна площадь сектора и его центральный угол
R = √ (360° * S) : (π * α), где S — площадь сектора круга, α — центральный угол.
Площадь сектора круга — это часть S всей фигуры, ограниченной окружностью с радиусом.
Если известна сторона вписанного правильного многоугольника
R = a : (2 * sin (180 : N)), где a — сторона правильного многоугольника, N — количество сторон.
В правильном многоугольнике все стороны равны.
Скачать онлайн таблицу
У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.
Прямоугольник. Онлайн калькулятор
С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ прямоугольника, радиус описанной вокруг прямоугольника окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.
Определение 1. Прямоугольник − это параллелограмм, у которого все углы прямые (Рис.1).
 |
Можно дать и другое определение прямоугольника.
Определение 2. Прямоугольник − это четырехугольник, у которого все углы прямые.
Свойства прямоугольника
Так как прямоугольник является параллелограммом, то все свойства параллелограмма верны и для прямоугольника.
- 1. Стороны прямоугольника являются его высотами.
- 2. Все углы прямоугольника прямые.
- 3. Квадрат диагонали прямоугольника равен сумме квадратов его соседних двух сторон.
- 4. Диагонали прямоугольника равны.
- 5. Около любого прямоугольника можно описать окружность, при этом диаметр описанной окружности равна диагонали прямоугольника.
Длиной прямоугольника называется более длинная пара его сторон.
Шириной прямоугольника называется более короткая пара его сторон.
Диагональ прямоугольника
Определение 3. Диагональ прямоугольника − это отрезок, соединяющий две несмежные вершины прямоугольника.
 |
На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. Прямоугольник имеет две диагонали.
Для вычисления длины диагонали воспользуемся теоремой Пифагора:
 |
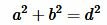 . . | (1) |
Из равенства (1) найдем d:
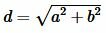 . . | (2) |
Пример 1. Стороны прямоугольника равны 
Решение. Для нахождения диаметра прямоугольника воспользуемся формулой (2). Подставляя 
 |
Ответ:
Окружность, описанная около прямоугольника
Определение 4. Окружность называется описанной около прямоугольника, если все вершины прямоугольника находятся на этой окружности (Рис.3):
 |
Формула радиуса окружности описанной около прямоугольника
Выведем формулу вычисления радиуса окружности, описанной около прямоугольника через стороны прямоугольника.
Нетрудно заметить, что радиус описанной около прямоугольника окружности равна половине диагонали (Рис.3). То есть
| ( small R=frac ) | (3) |
Подставляя (3) в (2), получим:
| ( small R=frac<large sqrt> ) | (4) |
Пример 2. Стороны прямоугольника равны 
Решение. Для нахождения радиуса окружности описанной вокруг прямоугольника воспользуемся формулой (4). Подставляя 
 |
 |
Ответ:
Периметр прямоугольника
Определение 5. Периметр прямоугольника − это сумма всех его сторон. Обозначается периметр латинской буквой P.
Периметр прямоугольника вычисляется формулой:
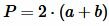 | (5) |
где ( small a ) и ( small b ) − стороны прямоугольника.
Пример 3. Стороны прямоугольника равны 
Решение. Для нахождения периметра прямоугольника воспользуемся формулой (5). Подставляя 
 |
Ответ:
Формулы сторон прямоугольника через его диагональ и периметр
Выведем формулу вычисления сторон прямоугольника, если известны диагональ ( small d ) и периметр ( small P ) прямоугольника. Заметим: чтобы прямоугольник существовал, должно удовлетворяться условие ( small frac P2>d ) (это следует из неравенства треугольника).
Чтобы найти стороны прямоугольника запишем формулу Пифагора и формулу периметра прямоугольника:
 | (6) |
 | (7) |
Из формулы (7) найдем ( small b ) и подставим в (6):
 | (8) |
 | (9) |
Упростив (4), получим квадратное уравнение относительно неизвестной ( small a ):
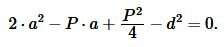 | (10) |
Вычислим дискриминант квадратного уравнения (10):
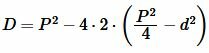 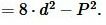 | (11) |
Сторона прямоугольника вычисляется из следующих формул:
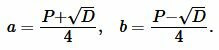 | (12) |
После вычисления ( small a ), сторона ( small b ) вычисляется или из формулы (12), или из (8).
Примечание. Легко можно доказать, что
| ( frac >d ; ⇒ ; P>2cdot d ; ⇒ ) ( small P^2>4 cdot d^2 ; ⇒ ; 4d^2-P^2 2d .) Следовательно выполняется неравенство (*). |
Пример 4. Диагональ прямоугольника равна 

Решение. Для нахождения сторон прямоугольника воспользуемся формулами (11), (12) и (8). Найдем сначала дискриминант ( small D ) из формулы (11). Для этого подставим 

 |
Подставляя значения 

 |
Найдем другую сторону ( small b ) из формулы (8). Подставляя значения 

 |
Ответ: 
Признаки прямоугольника
Признак 1. Если в параллелограмме диагонали равны, то этот параллелограмм является прямоугольником.
Признак 2. Если квадрат диагонали параллелограмма равен сумме квадратов его смежных сторон, то этот параллелограмм является прямоугольником.
Признак 3. Если углы параллелограмма равны, то этот параллелограмм является прямоугольником.














