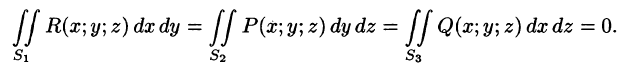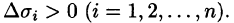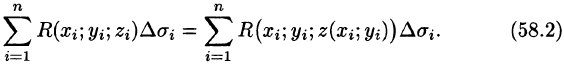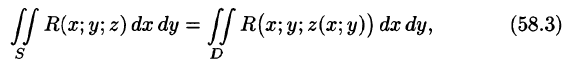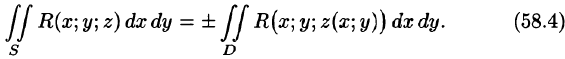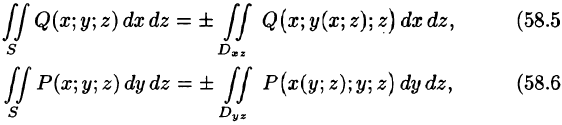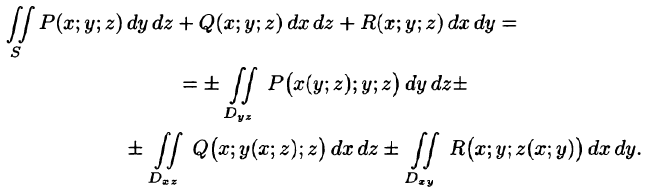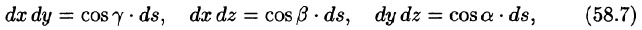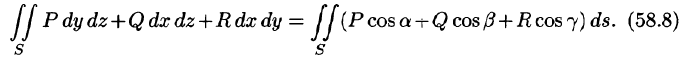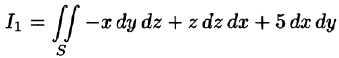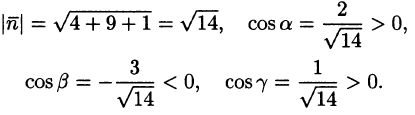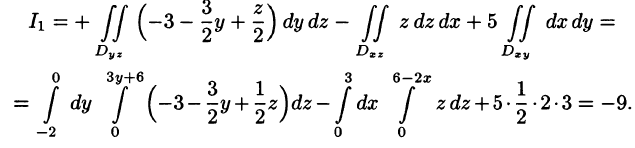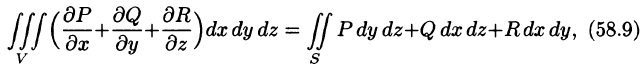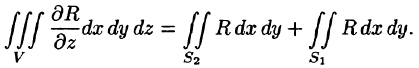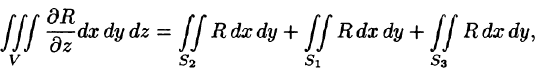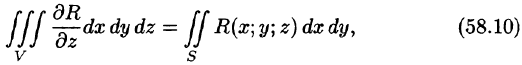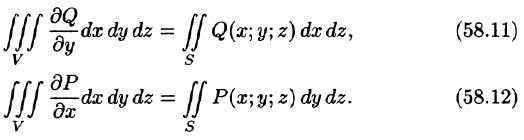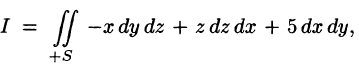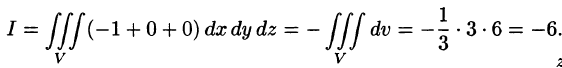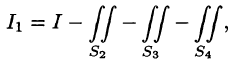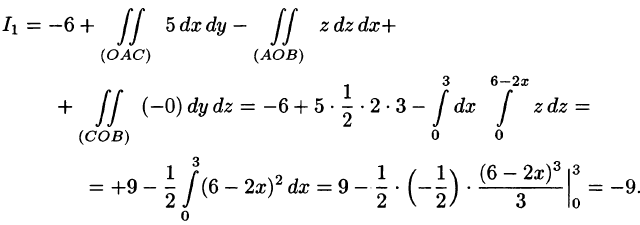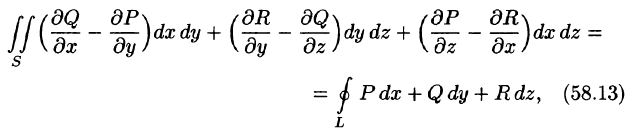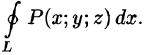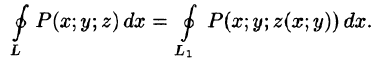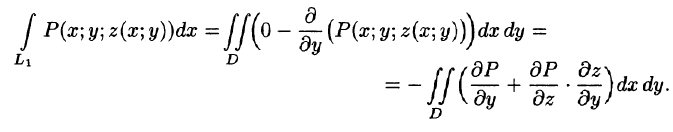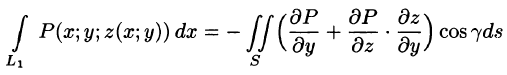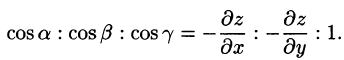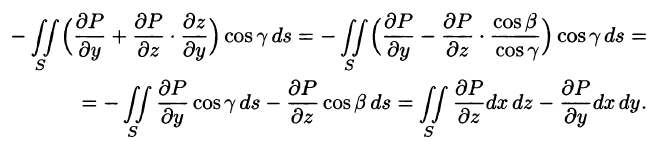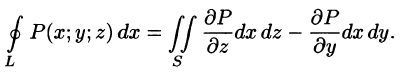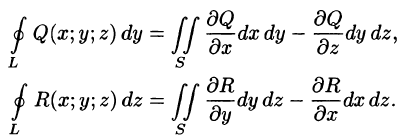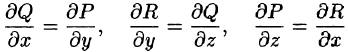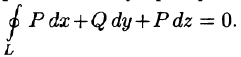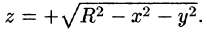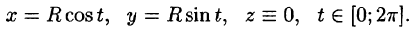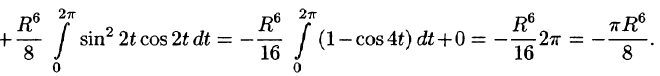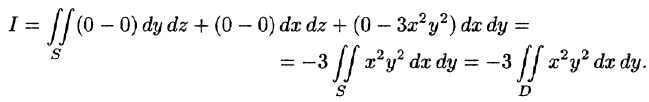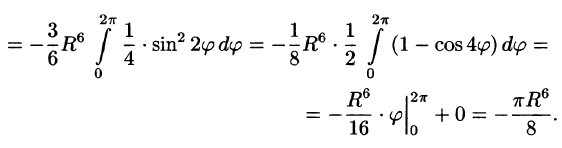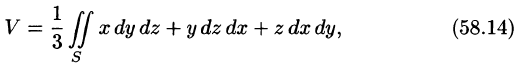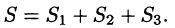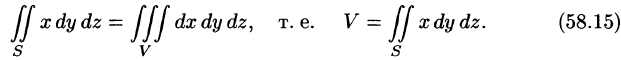- Понятие поверхностного интеграла первого рода
- Вычисление поверхностного интеграла первого рода
- Понятие поверхностного интеграла второго рода
- Вычисление поверхностного интеграла второго рода
- Больше примеров на вычисление поверхностных интегралов
- Поверхностные интегралы в математике с примерами решения и образцами выполнения
- Поверхностный интеграл первого рода
- Интеграл по цилиндрической поверхности
- Интеграл по сферической поверхности
- Определение и свойства поверхностных интегралов
- Поверхностный интеграл I рода
- Вычисление поверхностного интеграла I рода
- Некоторые приложения поверхностного интеграла I рода
- Площадь поверхности
- Масса поверхности
- Моменты, центр тяжести поверхности
- Поверхностный интеграл II рода
- Вычисление поверхностного интеграла II рода
- Формула Остроградского-Гаусса
- Формула Стокса
- Некоторые приложения поверхностного интеграла II рода
- Кратные, криволинейные и поверхностные интегралы (стр. 1 )
- 📹 Видео
Видео:Поток через замкнутую поверхность. Формула Остроградского-ГауссаСкачать

Понятие поверхностного интеграла первого рода
Поверхностный интеграл — обобщение понятия криволинейного интеграла на случаи, когда интегрирование происходит не по отрезку кривой, а по ограниченной поверхности. Как и криволинейные интегралы, поверхностные интегралы бывают первого рода и второго рода.
Поверхностный интеграл первого рода записывается в виде

где f(M) = f(x,y,z) – функция трёх переменных, а поверхность σ — область интегрирования этой функции. Если f(x,y,z) равна единице, то поверхностный интеграл равен площади поверхности.
Представьте себе довольно большой подсолнух с очень-очень маленькими семечками. Тогда по сумме поверхностей очень-очень маленьких семечек, расположенных на поверхности подсолнуха, можно вычислить поверхность подсолнуха — таким может быть упрощённое толкование поверхностного интеграла. Почему так?
Давайте перейдём к более формальному определению поверхностного интеграла. Поверхность σ разбита на n частей с площадями Δσ 1 , Δσ 2 , . Δσ n . Если выбрать на каждой частичной поверхности (семечке) произвольную точку M i с координатами (ζ i , η i , ς i ,) , то можно составить сумму

Эта сумма называется интегральной суммой для функции f(M) по поверхности σ . Теперь будем максимально увеличивать число таких маленьких частей, а наибольший диаметр Δσ i — наоборот, уменьшать. Если интегральная сумма при стремлении наибольшего из диаметров частей к нулю (то есть, как мы уже отмечали, все части очень маленькие) имеет предел, то этот предел и называется поверхностным интегралом первого рода от функции f(M) по поверхности σ .
Видео:Поток векторного поля через замкнутую поверхностьСкачать

Вычисление поверхностного интеграла первого рода
Вычисление поверхностного интеграла первого рода производится сводением к двойному интегралу.
Пусть поверхность σ задана уравнением z = z(x, y) , её проекцией на плоскость xOy является область D xy , при этом функция z = z(x, y) и её частные производные 

Это и есть формула, выражающая поверхностный интеграл первого рода через двойной интеграл по проекции поверхности σ на плоскость xOy.
Пример 1. Вычислить поверхностный интеграл первого рода
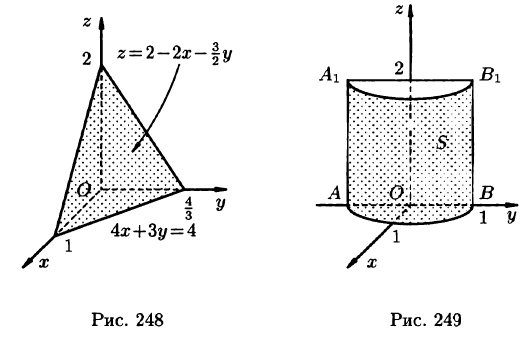
где σ — часть плоскости 
Из уравнения плоскости получаем выражение «зет»: 
Тогда частные производные: 


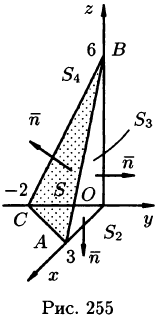
Поверхность σ является изображённым на чертеже треугольником ABC , а его проекцией на плоскость xOy — треугольником AOB , который ограничен прямыми x = 0 , y = 0 и 3x + y = 6 . От поверхностного интеграла перейдём к двойному интегралу и решим его:

Видео:Поток векторного поля через поверхность. Поверхностный интеграл.Скачать
Понятие поверхностного интеграла второго рода
Прежде чем перейти к определению поверхностного интеграла второго рода, требуется познакомиться с понятиями стороны поверхностей и ориентированных поверхностей.
Пусть в пространстве дана гладкая поверхность σ. На этой поверхности выберем произвольную точку M и проведём через неё вектор нормали 
Если направление вектора нормали не поменяется, то поверхность σ называется двусторонней. Если же при обходе контура направление вектора нормали поменяется на противоположное, то поверхность называется односторонней. Двусторонние поверхности называются ориентированными поверхностями, односторонние — неориентированными поверхностями.
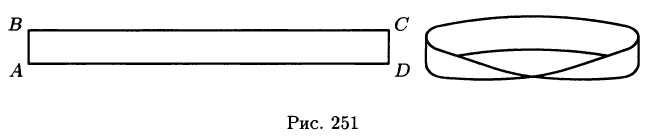
Пример односторонней поверхности — лист Мёбиуса (на рисунке выше), который можно сделать из полоски бумаги, одна сторона которой повёрнута на 180 градусов, и затем концы склеены. И вот что здесь важно: для односторонней поверхности понятие поверхностного интеграла второго рода не вводится.
Так что будем рассматривать только двусторонние поверхности. Примеры двусторонних поверхностей — плоскости, сфера, эллипсоил, параболоид.
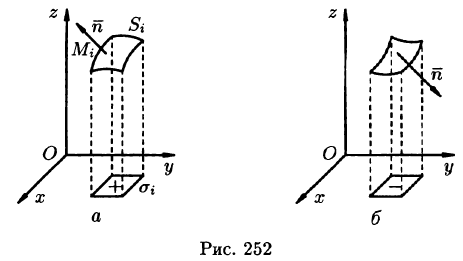
Положительную сторону двустороней поверхности определяет направление вектора нормали. Противоположная сторона поверхности называется отрицательной. Положительной стороной поверхности называется её верхняя сторона. Если единичные векторы нормали составляют острые углы с осью Oz, то выбрана верхняя сторона поверхности z = z(x, y) , если углы тупые, то нижняя сторона поверхности.
Как и в случае поверхностного интеграла первого рода, поверхность можно разбить на n частей. При формулировке понятия поверхностного интеграла первого рода в интегральной сумме присутствовали площади каждой из частей, на которые умножаются значения функции f(M i ) . В случае поверхностного интеграла второго рода берутся площади не самих частей, а площади их проекций на координатные плоскости. А функцию трёх переменных для отличия от интеграла первого рода обозначим R(x,y,z) . Тогда интегральная сумма запишется так:

где Δs i — площади упомянутых проекций частей стороны поверхности на координатную ось (пока будем считать, что на ось xOy).
При таких соглашениях и обозначениях определение поверхностного интеграла второго рода аналогично определению интеграла первого рода. А именно: поверхностным интегралом второго рода называется предел данной интегральной суммы при стремлении к нулю наибольшего из диаметров частей рассматриваемой поверхности.
Записывается он так:

В данном случае функция R(x,y,z) интегрируема по переменным x и y, так как части поверхности проецировались на плоскость xOy.
Аналогично можно записать и два других поверхностных интеграла второго рода:
(функция P(x,y,z) интегрируема по переменным y и z, так как части поверхности проецируются на плоскость yOz),
(функция Q(x,y,z) интегрируема по переменным z и x, так как части поверхности проецируются на плоскость zOx).
Сумма этих интегралов
называется общим поверхностным интегралом второго рода и обозначается
Видео:Формула Остроградского-ГауссаСкачать

Вычисление поверхностного интеграла второго рода
Поверхностный интеграл второго рода вычисляется путём разложения общего поверхностного интеграла второго рода на сумму поверхностных интегралов (см. окончание предыдущего параграфа) и сведением каждого из них к двойному интегралу.
Рассмотрим подробно вычисление интеграла

Пусть поверхность σ задана уравнением z = z(x, y) . Положительную сторону поверхности обозначим 

Таким образом, получаем формулу для вычисления поверхностного интеграла второго рода:

Если выбрана отрицательная сторона поверхности, то знак интеграла меняется:

Аналогично вычисляются два других отдельных интеграла — слагаемых общего:


Пример 2. Вычислить поверхностный интеграл второго рода

где σ — верхняя сторона части плоскости 
Решение. Чертёж — на рисунке сверху. По определению получаем сумму трёх двойных интегралов:
Второй интеграл равен нулю, так как плоскость σ параллельна оси Oy . Поэтому найдём первый и третий интегралы:
Остаётся лишь сложить все отдельные интегралы и получить общий поверхностный интеграл второго рода:

Если требуется вычислить поверхностный интеграл второго рода по замкнутой поверхности, можно перейти к тройному интегралу, используя формулу Остроградского. Тогда, если функции P(x,y,z) , Q(x,y,z) и R(x,y,z) и их частные производные 


Пример 3. Вычислить поверхностный интеграл второго рода

где σ — внешняя сторона поверхности конуса, образованного поверхностью 
Решение. Данная поверхность является поверхностью конуса с радиусом R = 2 и высотой h = 2 . Это замкнутая поверхность, поэтому можно использовать формулу Остроградского. Так как P = 3x , Q = 4y , R = −z , то частные производные 


Переходим к тройному интегралу, который и решаем:
Видео:Формула Стокса.ЦиркуляцияСкачать

Больше примеров на вычисление поверхностных интегралов
Пример 4. Вычислить поверхностный интеграл первого рода

где σ — боковая поверхность конуса 

Решение. Так как частные производные 

Сводим данный поверхностный интеграл к двойному:

Проекцией поверхности на плоскость xOy является круг с центром в начале координат и радиусом R = 2 , поэтому при вычислении двойного интеграла перейдём к полярной системе координат. Для этого сделаем замену переменных:
Получаем следующий интеграл, который окончательно и решаем:
Пример 5. Вычислить поверхностный интеграл второго рода

где σ — верхняя часть треугольника, образованного пересечением плоскости 
Решение. Данный поверхностный интеграл разделим на сумму двух интегралов



Чтобы вычислить интеграл I 1 , построим проекцию поверхности σ на плоскость yOz. Проекцией является треугольник OCB , который на плоскости yOz ограничивают прямые 


Чтобы вычислить интеграл I 2 , построим проекцию поверхности σ на плоскость zOx. Проекцией является треугольник AOC , который ограничивают прямые 

Складываем два полученных интеграла и окончательно получаем данный поверхностный интеграл:

Пример 6. Вычислить поверхностный интеграл второго рода

где σ — внешняя поверхность пирамиды, образованной плоскостью 
Решение. Данный поверхностный интеграл вычислим двумя способами
1) интегрируя по каждой грани пирамиды;
2) используя формулу Остроградского.
1) Вычисление интегрированием по каждой грани пирамиды.
а) Вычислим интеграл по треугольнику ABC . Для этого разделим интеграл на сумму трёх интегралов, которые отдельно решим:

Складываем и получаем:

б) Вычислим поверхностный интеграл по треугольнику AOB , который находится в плоскости z = 0 . Тогда dz = 0 и, учитывая, что нормальный вектор плоскости образует с осью Oz тупой угол, получаем
в) Треугольник AOC находится в плоскости y = 0 , таким образом, dy = 0 и (нормальный вектор плоскости образует с осью Oy тупой угол) получаем
г) Осталось вычислить поверхностный интеграл по треугольнику CBO находится в плоскости x = 0 , таким образом, dx = 0 и получаем

В результате получаем данный поверхностный интеграл второго рода:

2) Используя формулу Остроградского, от поверхностного интеграла по замкнутой поверхности перейдём к тройному интегралу, где W — область, ограниченная поверхностью σ . Так как P = xz , Q = 1 , R = 2y , то частные производные 


Получаем следующее решение данного поверхностного интеграла:
В последнем примере вернёмся к вычислению поверхностного интеграла первого рода.
Пример 7. Вычислить площадь поверхности параболоида 

Решение. Определим, при каком значении z данные поверхности пересекаются:
Значение −3 не подходит, поэтому остаётся только z = 1 .
Обозначим через C часть поверхности данного параболоида во внутреней стороне сферы. Проекция поверхности C (обозначим её D ) на плоскость xOy является кругом с центром в начале координат и радиусом √2 , так как при z = 1 получаем уравнение окружности 


Проекцией поверхности на плоскость xOy является круг, поэтому при вычислении двойного интеграла перейдём к полярной системе координат. Для этого сделаем замену переменных:
Получаем окончательное решение данного поверхностного интеграла:
Видео:Непосредственное вычисление потокаСкачать

Поверхностные интегралы в математике с примерами решения и образцами выполнения
При изучении темы «Поверхностные интегралы» вы познакомитесь с понятием интеграла по поверхности от функции трех
переменных и научитесь сводить его к двойному (а затем — к повторному), проецируя заданную поверхность на одну из координатных плоскостей. Кроме того, вы научитесь вычислять интегралы по части цилиндрической и сферической поверхностей.
Видео:Найти поток векторного поля через замкнутую поверхность S (нормаль внешняя).Скачать

Поверхностный интеграл первого рода
Постановка задачи. Вычислить поверхностный интеграл
где 
и некоторыми неравенствами.
План решения. Поверхностный интеграл сводится к двойному
проецированием 
где D — проекция 
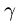
к поверхности 
Замечание:
Если уравнение F(x,y,z) = 0 не определяет однозначно функцию z = z(x,y), то проецируем 
также разбить поверхность на части и воспользоваться аддитивностью интеграла).
1.Единичные нормальные векторы 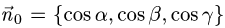
2.Проекцию D поверхности 

3.Находим z = z(x, у), решая уравнение F(x, у, z) = 0.
4.Переходим от поверхностного интеграла к двойному по формуле (1) и вычисляем двойной интеграл, сводя его к повторному.
Пример:
Вычислить поверхностный интеграл
где 
расположенная в первом октанте (т.е. 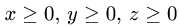
Решение:
1.Единичные нормальные векторы 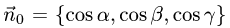
поверхности, заданной уравнением F(x, у, z) = 0, определяются формулой
В данном случае F(x,y,z) = х + 2у + 3z — 1. Следовательно,
2.Поверхность 
Ее проекцию D на плоскость XOY находим, исключая z из условий,
определяющих 
3.Из уравнения х + 2у + 3z — 1 = 0 находим z(x, у) = (1 — х — 2у)/3.
4.Переходим от поверхностного интеграла к двойному по формуле (1) и вычисляем двойной интеграл, сводя его к повторному:
Ответ.
Интеграл по цилиндрической поверхности
Постановка задачи. Вычислить поверхностный интеграл
где 
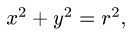
z = 0 и z = h.
1.Вводим на заданной поверхности (цилиндре) криволинейные
координаты
В этих координатах поверхность задается условиями
3.Вычисляем повторный интеграл и записываем ответ.
Пример:
Вычислить поверхностный интеграл
где 
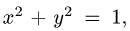
z = 0, z = 2.
Решение:
1.Вводим на заданной поверхности (цилиндре) криволинейные
координаты
В этих координатах поверхность задается условиями
2.Так как 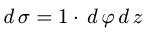
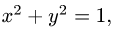
3.Вычисляем повторный интеграл:
Ответ.
Интеграл по сферической поверхности
Постановка задачи. Вычислить поверхностный интеграл
где 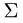
1.Вводим на заданной поверхности (сфере) криволинейные координаты
В этих координатах поверхность задается условиями
2.Так как 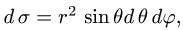
3.Вычисляем повторный интеграл и записываем ответ.
Пример:
Вычислить поверхностный интеграл
где 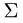
Решение:
1.Вводим на заданной поверхности (сфере) криволинейные координаты
В этих координатах поверхность задается условиями
2.Так как 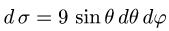
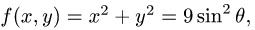
3.Вычисляем повторный интеграл:
Ответ.
Видео:Математический анализ, 47 урок, Криволинейные интегралы первого родаСкачать

Определение и свойства поверхностных интегралов




Видео:Поверхностный интеграл II родаСкачать

Поверхностный интеграл I рода
Обобщением двойного интеграла является так называемый поверхностный интеграл.
Пусть в точках некоторой поверхности S, с площадью S , пространства Oxyz определена непрерывная функция f(х; у; z). Разобьем поверхность S на п частей 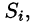
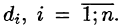
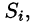
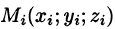
Она называется интегральной для функции f(x;y;z) по поверхности S.
Если при 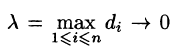
Таким образом, по определению,
Отметим, что «если поверхность S гладкая (в каждой ее точке существует касательная плоскость, которая непрерывно меняется с перемещением точки по поверхности), а функция f(x;y;z) непрерывна на этой поверхности, то поверхностный интеграл существует» (теорема существования).
Поверхностный интеграл I рода обладает следующими свойствами:
3. Если поверхность S разбить на части 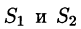
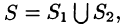
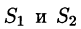
4.Если на поверхности S выполнено неравенство
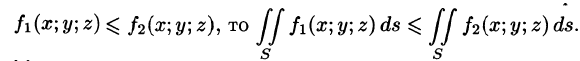
7.Если f(x; у, z) непрерывна на поверхности S, то на этой поверхности существует точка 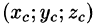
(теорема о среднем значении).
Видео:Демидович №4441б: поток радиус-вектора через замкнутую поверхностьСкачать

Вычисление поверхностного интеграла I рода
Вычисление поверхностного интеграла I рода сводится к вычислению двойного интеграла по области D — проекции поверхности S на плоскость Оху.
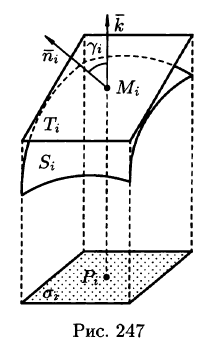
Разобьем поверхность S на части 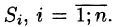
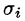
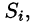
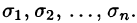
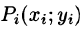
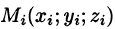
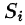
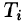
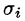
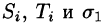
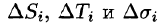

Обозначив через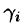
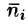
(область 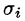
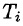
Если поверхность S задана уравнением z = = z(x;y), то, как известно (см. (45.2)), уравнение касательной плоскости в точке 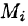
где 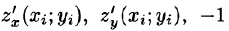
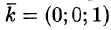
Равенство (57.4) принимает вид
В правой части формулы (57.2) заменим 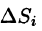
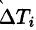
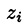
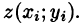
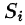
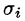
выражающую интеграл по поверхности S через двойной интеграл по проекции S на плоскость Оху.
Отметим, что если поверхность S задана уравнением вида у = y(x;z) или х = x(y;z), то аналогично получим:
где 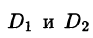
Пример:
Вычислить 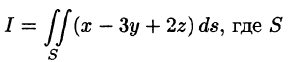
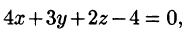
Решение:
Запишем уравнение плоскости в виде
Находим 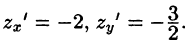
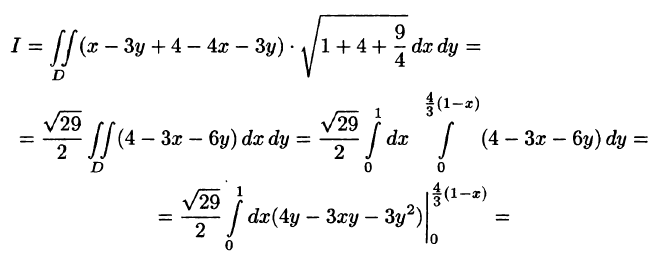
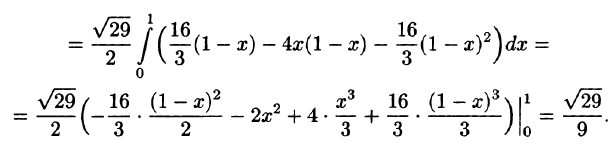
Пример:
где S — часть цилиндрической поверхности 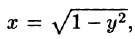
Решение:
Воспользуемся формулой (57.6). Поскольку
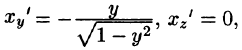
то где 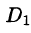
Некоторые приложения поверхностного интеграла I рода
Приведем некоторые примеры применения поверхностного интеграла I рода.
Площадь поверхности
Если поверхность S задана уравнением z = z(x; у), а ее проекция на плоскость Оху есть область D, в которой z(x;y), zx'(x; у) и zy'(x;y) — непрерывные функции, то ее площадь S вычисляется по формуле
Кроме того, поверхностный интеграл применяют для вычисления массы, координат центра масс, моментов инерции материальных поверхностей с известной поверхностной плотностью распределения массы 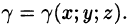
Масса поверхности
Пусть плотность распределения массы материальной поверхности есть 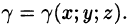
- Разбиваем поверхность S на п частей
площадь которой обозначим
.
- Берем произвольную точку
в каждой области
. Предполагаем, что в пределах области
плотность постоянна и равна значению ее в точке
.
- Масса
области
мало отличается от массы
фиктивной однородной области с постоянной плотностью
4. Суммируя 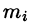
5.За точное значение массы материальной поверхности S принимается предел, к которому стремится полученное приближенное значение при стремлении к нулю диаметров областей 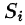
Моменты, центр тяжести поверхности
Статистические моменты, координаты центра тяжести, моменты инерции материальной поверхности S находятся по соответствующим формулам:
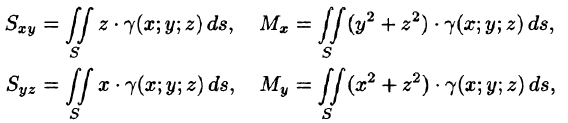
Пример:
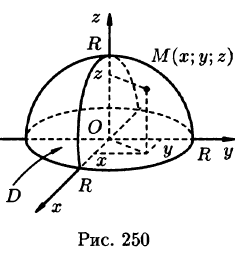
Найти массу полусферы радиуса R, если в каждой точке поверхности плотность численно равна расстоянию этой точки от радиуса, перпендикулярного основанию полусферы. Решение: На рисунке 250 изображена полусфера радиуса R. Ее уравнение 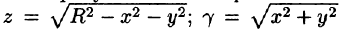
По формуле (57.7) находим:
Переходим к полярным координатам:
внутренний интеграл вычислен с помощью подстановки r= Rsint:
Видео:41. Основные понятия теории векторных полейСкачать

Поверхностный интеграл II рода
Поверхностный интеграл II рода строится по образцу криволинейного интеграла II рода, где направленную кривую разлагали на элементы и проектировали их на координатные оси; знак брали в зависимости от того, совпадало ли ее направление с направлением оси или нет.
Пусть задана двусторонняя поверхность (таковой является плоскость, эллипсоид, любая поверхность, задаваемая уравнением z =f(x;y), где f(x;y), 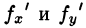
Далее, пусть в точках рассматриваемой двусторонней поверхности S в пространстве Oxyz определена непрерывная функция f(x; у; z). Выбранную сторону поверхности (в таком случае говорят, что поверхность ориентирована) разбиваем на части 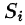
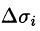
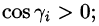
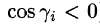
где 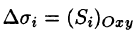
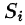
Предел интегральной суммы (58.1) при 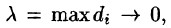
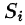
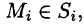
Аналогично определяются поверхностные интегралы II рода по переменным у и z и z и х:
Общим видом поверхностного интеграла II рода служит интеграл
где P, Q, R — непрерывные функции, определенные в точках двусторонней поверхности S.
Отметим, что если S — замкнутая поверхность, то поверхностный интеграл по внешней стороне ее обозначается 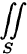
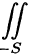
Из определения поверхностного интеграла II рода вытекают следующие его свойства:
- Поверхностный интеграл II рода изменяет знак при перемене стороны поверхности.
- Постоянный множитель можно выносить за знак поверхностного интеграла.
- Поверхностный интеграл от суммы функций равен сумме соответствующих интегралов от слагаемых.
- Поверхностный интеграл II рода по всей поверхности
равен сумме интегралов по ее частям
(аддитивное свойство), если
пересекаются лишь по границе, их разделяющей.
- Если
— цилиндрические поверхности с образующими, параллельными соответственно осям Oz, Ох, Оу, то
Видео:Непосредственное вычисление циркуляцииСкачать

Вычисление поверхностного интеграла II рода
Вычисление поверхностного интеграла II рода сводится к вычислению двойного интеграла.
Пусть функция R(x; у, z) непрерывна во всех точках поверхности S, заданной уравнением z = z(x; y), где z(x; у) — непрерывная функция в замкнутой области D (или 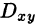
Выберем ту сторону поверхности S, где нормаль к ней образует с осью Oz острый угол. Тогда
Так как 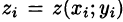
Правая часть этого равенства есть интегральная сумма для функции R(x;y;z(x;y)), непрерывной в области D. Переходя к пределу в равенстве (58.2) при 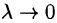
выражающую поверхностный интеграл II рода по переменным х и у через двойной интеграл. Если выбрать вторую сторону, т. е. нижнюю, поверхности S, то полученный двойной интеграл берут со знаком «минус». Поэтому
где 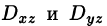
В формуле (58.5) поверхность S задана уравнением у = y(x;z), а в формуле (58.6) — уравнением х = x(y;z). Знаки перед интегралами выбираются в зависимости от ориентации поверхности S (так, в формуле (58.5) берем знак «плюс», если нормаль к поверхности образует с осью Оу острый угол, а знак «минус» — если тупой угол).
Для вычисления общего поверхностного интеграла II рода используют формулы (58.4)-(58.6), проектируя поверхность S на все три координатные плоскости:
Замечание:
Можно показать справедливость равенств
— элемент площади поверхности 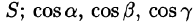
Поверхностные интегралы I и II рода связаны соотношением
Пример:
по верхней стороне части плоскости 2х — Зу + z = 6, лежащей в IV октанте.
Решение:
На рисунке 253 изображена заданная часть плоскости. Нормаль п, соответствующая указанной стороне поверхности, образует с осью Оу тупой угол, а с осями Ох и Oz — острые. В этом можно убедиться, найдя направляющие косинусы нормального вектора 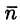
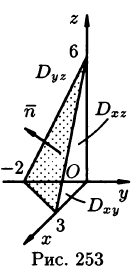
Поэтому перед двойными интегралами в формулах (58.4) и (58.6) следует брать знак «плюс», а в формуле (58.5) — знак «минус». Следовательно,
Формула Остроградского-Гаусса
Связь между поверхностным интегралом II рода по замкнутой поверхности и тройным интегралом по объему, ограниченному этой поверхностью устанавливает следующая теорема.
Теорема:
Если функции P(x;y;z), Q(x;y,z), R(x;y;z) непрерывны вместе со своими частными производными первого порядка в пространственной области V, то имеет место формула
где S — граница области V и интегрирование по S производится по ее внешней стороне.
Формула (58.9) называется формулой Остроградского-Гаусса (является аналогом формулы Остроградского-Грина (см. п. 56.3).
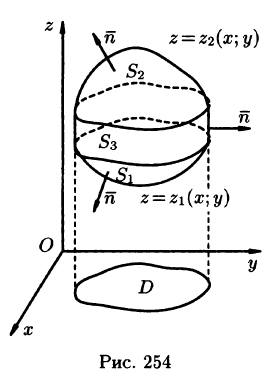
Пусть область V ограничена снизу поверхностью 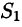
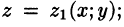
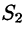
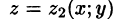
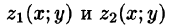
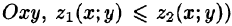
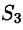
Рассмотрим тройной интеграл
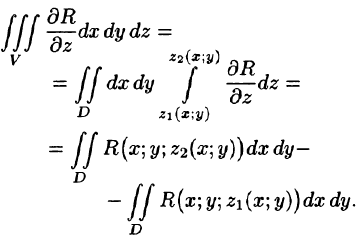
Двойные интегралы в правой части равенства заменим поверхностными интегралами II рода по внешней стороне поверхностей 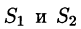
Добавляя равный нулю интеграл 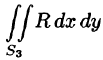
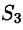
где S — поверхность, ограничивающая область V. Аналогично доказываются формулы
Складывая почленно равенства (58.10), (58.11) и (58.12), получаем формулу (58.9) Остроградского-Гаусса.
Замечания:
- Формула (58.9) остается справедливой для любой области V, которую можно разбить на конечное число областей рассмотренного вида.
- Формулу Остроградского-Гаусса можно использовать для вычисления поверхностных интегралов II рода по замкнутым поверхностям.
Пример:
где S — внешняя сторона пирамиды, ограниченной плоскостями 2х — Зу + z = 6, х = 0, у = 0, z = 0.
Решение:
По формуле (58.9) находим:
Заметим, что интеграл 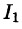
где поверхности 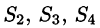
Формула Стокса
Связь между поверхностными и криволинейными интегралами II рода устанавливает следующая теорема.
Теорема:
Если функции P(x;y;z), Q(x;y;z) и R(x;y;z) непрерывны вместе со своими частными производными первого порядка в точках ориентированной поверхности S, то имеет место формула
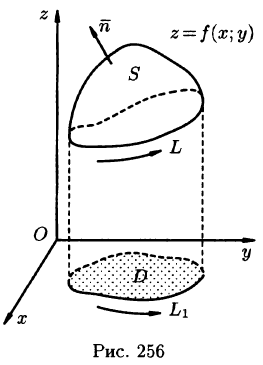
где L — граница поверхности S и интегрирование вдоль кривой L производится в положительном направлении (т. е. при обходе границы L поверхность S должна оставаться все время слева).
Формула (58.13) называется формулой Стокса (Д. Г. Стоке — английский математик, физик).
Пусть z = f(x;y) — уравнение поверхности S, функции 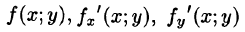
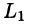
Будем считать, что поверхность S пересекается с любой прямой, параллельной оси Oz, не более чем в одной точке. Выберем верхнюю сторону поверхности S. Рассмотрим сначала интеграл вида
Значения функции Р(х; у; z) на L равны значениям функции P(x; y;z(x;y)) на 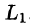
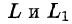
Применим к этому интегралу формулу Остроградского-Грина (см. п. 56.3). Тогда получим:
Преобразуем полученный двойной интеграл в равный ему поверхностный интеграл II рода (см. п. 58.2). Для этого последнее равенство перепишем в виде
(см. 58.7) и используем уравнение нормали к поверхности S (см. (45.3)). Так как выбрана верхняя сторона поверхности S, т. е. 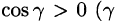
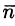
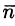
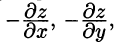
Отсюда 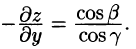
Аналогично получаются при соответствующих условиях еще два равенства:
Складывая почленно три последних равенства, получаем формулу Стокса (58.13).
Отметим, что формулу Стокса (58.13) можно применить и для поверхностей более сложного вида (разбив ее на части рассмотренного выше типа).
Формулу Стокса можно применять для вычисления криволинейного интеграла по замкнутому контуру с помощью поверхностного интеграла.
Из формулы Стокса вытекает, что если выполняются условия
то криволинейный интеграл по произвольному пространственному замкнутому контуру L равен нулю:
Следовательно, в данном случае криволинейный интеграл не зависит от вида пути интегрирования.
Пример:
Вычислить 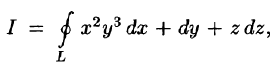
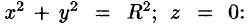
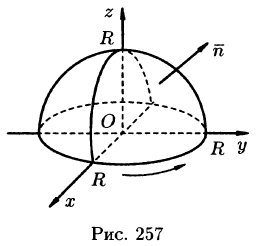
б) используя формулу Стокса, взяв в качестве поверхности полусферу
Решение: Поверхность интегрирования изображена на рисунке 257.
а) Запишем уравнение окружности в параметрической форме:
По формуле (56.7) имеем:
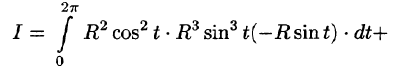
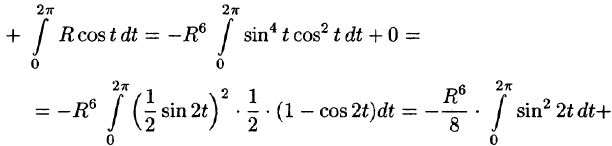
б) По формуле Стокса (58.13) находим:
Переходя к полярным координатам, получаем:
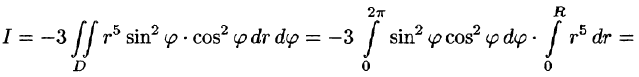
Некоторые приложения поверхностного интеграла II рода
С помощью поверхностного интеграла 11 рода можно найти объем тела, ограниченного сверху поверхностью 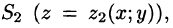
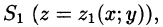
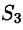
где
Действительно, положив в формуле Остроградского-Гаусса (58.9) 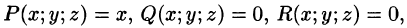
Аналогично, полагая P = 0, Q = у, R = 0, находим еще одну формулу для нахождения объема тела с помощью поверхностного интеграла II рода:
Наконец, положив Р = 0, Q = 0, R = z, по формуле (58.9) находим третью формулу
выражающую объем тела через поверхностный интеграл II рода.
Сложив почленно равенства (58.15)-(58.17) и разделив на три, получим формулу (58.14).
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Видео:Демидович №4442: поток вектора через цилиндрСкачать

Кратные, криволинейные и поверхностные интегралы (стр. 1 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 |
КРАТНЫЕ, КРИВОЛИНЕЙНЫЕ И ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ.
I. Кратные интегралы
1. Двойной интеграл
Рассмотрим в плоскости Оху замкнутую область D, ограниченную линией L. Разобьем эту область какими-нибудь линиями на п частей 

Пусть в области D задана функция z = f(x, y). Обозначим через f(P1), f(P2),…, f(Pn) значения этой функции в выбранных точках и составим сумму произведений вида f(Pi)ΔSi :

называемую интегральной суммой для функции f(x, y) в области D.
Если существует один и тот же предел интегральных сумм (1) при 


Вычисление двойного интеграла по области D, ограниченной линиями 
Связь между полярными и декартовыми координатами точки М можно задать, если совместить начало декартовой системы координат с полюсом, а положительную полуось Ох – с полярной осью (рис. 3). Тогда x=ρcosφ, у=ρsinφ . Отсюда 

📹 Видео
Семинар 10. Поверхностный интеграл первого рода.Скачать

Формула ГринаСкачать

ПОВЕРХНОСТНЫЙ ИНТЕГРАЛ ВТОРОГО РОДАСкачать

Демидович №4441а: поток радиус-вектора через конусСкачать

Семинар 12. Формула Остроградского — Гаусса.Скачать

2421. Формула Остроградского.Скачать



































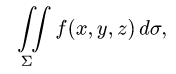
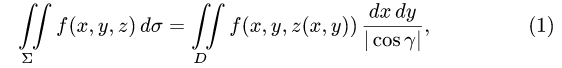
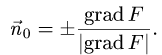
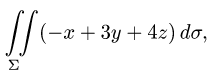
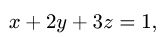
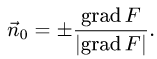
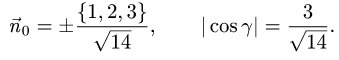
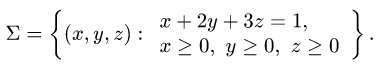
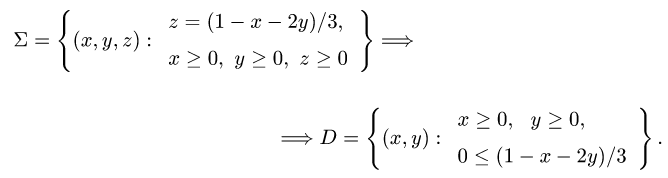
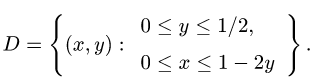
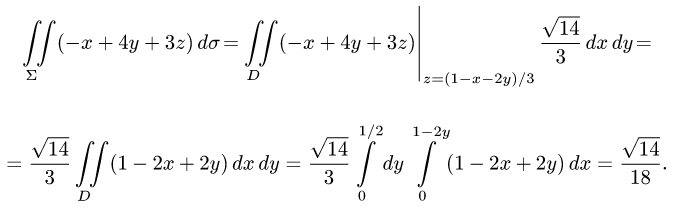
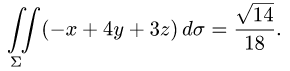
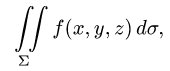
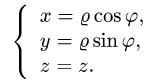
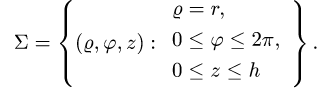
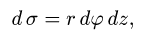
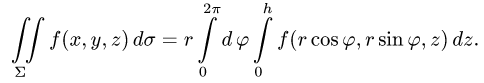
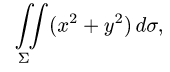
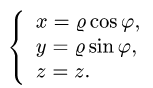
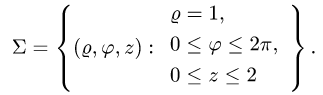
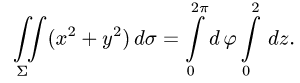
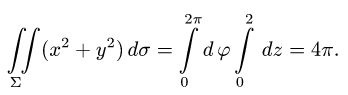
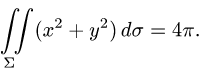
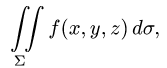
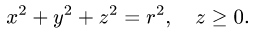
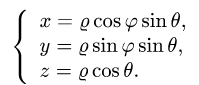
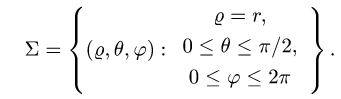
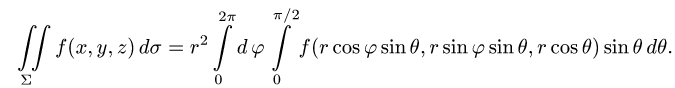
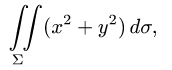
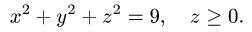
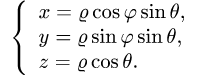
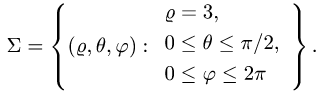
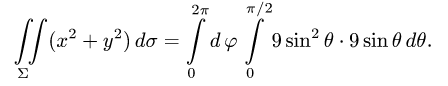
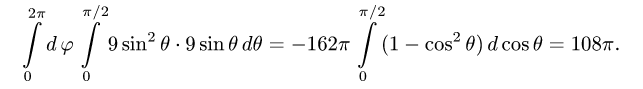
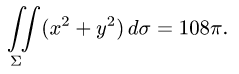


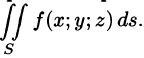
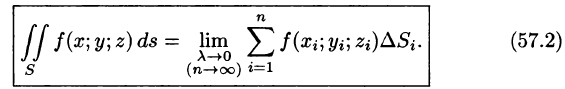
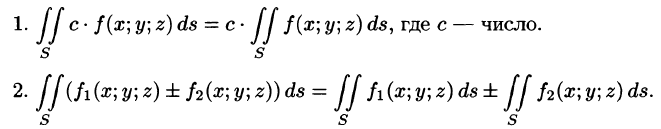
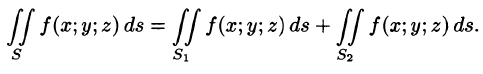
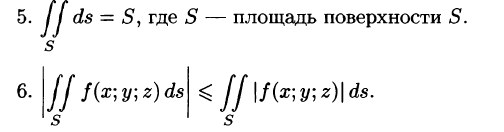
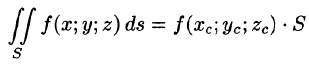
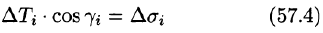
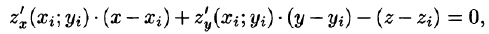
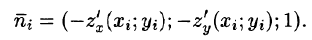
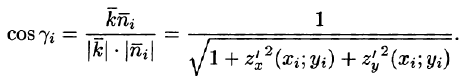
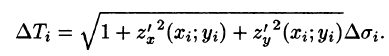
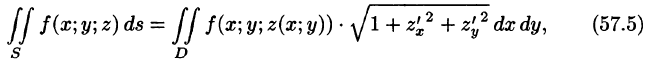
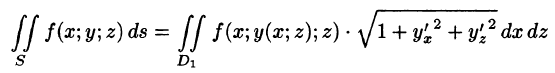
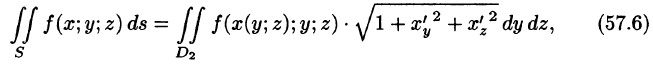
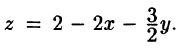
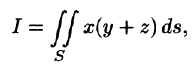
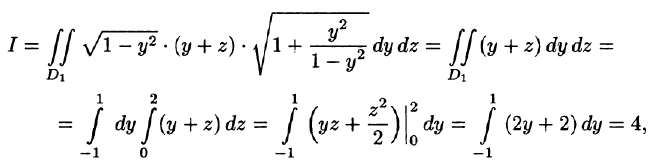
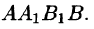
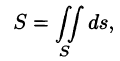
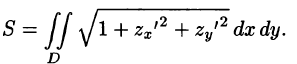
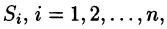 площадь которой обозначим
площадь которой обозначим 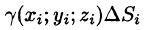 фиктивной однородной области с постоянной плотностью
фиктивной однородной области с постоянной плотностью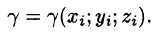
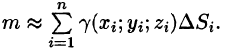
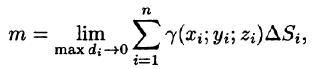
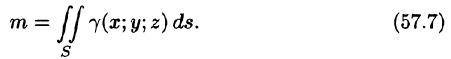
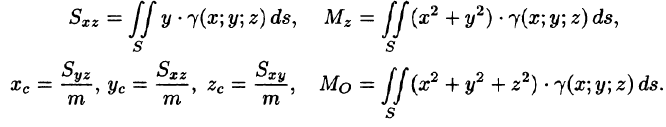
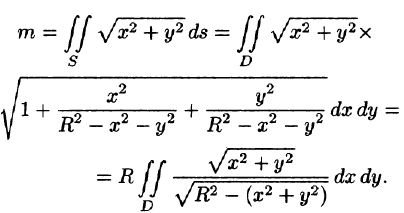
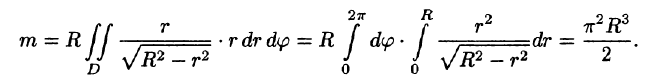
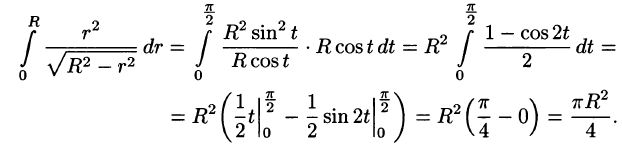

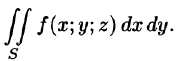
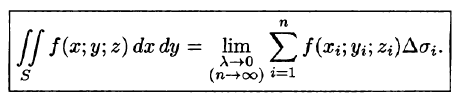
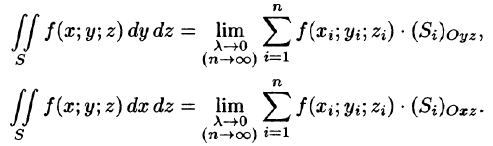
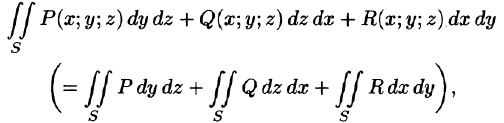
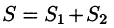 равен сумме интегралов по ее частям
равен сумме интегралов по ее частям 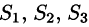 — цилиндрические поверхности с образующими, параллельными соответственно осям Oz, Ох, Оу, то
— цилиндрические поверхности с образующими, параллельными соответственно осям Oz, Ох, Оу, то