Вопрос по геометрии:
Темой проведённой через вершину в треугольника ABC параллельно стороне AC образует со сторонами BA и BC равные углы Определите вид треугольника ABC. Помагите пожалуйста плиз
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!
- Как написать хороший ответ?
- теорема Менелая презентация к уроку по геометрии (11 класс) на тему
- Скачать:
- Предварительный просмотр:
- Подписи к слайдам:
- Подписи к слайдам:
- В треугольнике ABM через вершину В проведена прямая D, параллельная стороне АM?
- Через середину К медианы ВМ треугольника АВС и вершину А проведена прямая, пересекающая сторону ВС в точке Р?
- Через вершину с треугольника авс проведена прямая параллельная биссектрисе AM треугольника и пересекающая прямую AB в точке K?
- В равнобедренном прямоугольном треугольнике медиана, проведенная из вершины прямого угла, равна 5 см?
- В равнобедренном треугольнике ABC с вершиной B проведена медиана AM к боковой стороне?
- Дан треугольник АВС?
- Через середину К медианы BM треугольника АБС и вершину А проведена прямая, пересекающая сторону ВС в точкее Р?
- В треугольнике проведена высота из вершины прямого угла Докажите что данный треугольник из — за образовавшейся треугольника имеют соответственно равные углы?
- Постройте произвольный треугольник ?
- В прямоугольнике ABCD проведена биссектриса AM?
- Дан треугольник ABC?
- 📽️ Видео
Ответы и объяснения 1
Знаете ответ? Поделитесь им!
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
- Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
- Писать без грамматических, орфографических и пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
- Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
- Использовать мат — это неуважительно по отношению к пользователям;
- Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!
Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.
Видео:№199. Прямая р параллельна стороне АВ треугольника ABC. Докажите, что прямые ВССкачать

теорема Менелая
презентация к уроку по геометрии (11 класс) на тему
теорема Менелая в задачах
Видео:№473. Через вершину С треугольника ABC проведена прямая m, параллельная стороне АВ. Докажите,Скачать

Скачать:
| Вложение | Размер |
|---|---|
| применение теоремы Менелая к задачам | 1.29 МБ |
| kopiya_teorema_menelaya.pptx | 1.29 МБ |
Бесплатный марафон подготовки к ЕГЭ на зимних каникулах
Учи.Дома запускает бесплатный марафон в котором каждый день. В течении 5 дней утром ты будешь получать одно задание по выбранному предмету, а вечером его решение. Твоя задача, успеть выполнение задание до того как получишь ответ.
Бесплатно, онлайн, подготовка к ЕГЭ
Предварительный просмотр:
Видео:Через середину К медианы ВМ треугольника АВС и вершину А проведена прямая пересекающая сторону ВС вСкачать

Подписи к слайдам:
Изучить теорему. Знать её применение. Уметь решать задачи на изученную теорему. Задачи:
В курсе геометрии 7-х –9-х классов были рассмотрены важные и интересные свойства геометрических фигур на плоскости. Но многие удивительные соотношения и изящные геометрические факты не вошли в основной курс. Из школьного курса нам известны теоремы о замечательных точках в треугольнике: три биссектрисы (медианы, высоты) пересекаются в одной точке. Эти свойства являются следствиями теоремы Менелая . Введение
Биография ученого Менела́й Александри́йский — древнегреческий математик и астроном, создатель системы геометрии и тригонометрии на сфере – первой неевклидовой геометрии. Время его жизни и деятельности определяется приведёнными в « Алмагесте » Птолемея двумя астрономическими наблюдениями, которые Менелай произвёл в Риме в первом году царствования Траяна, то есть в 98 году н. э. Его работы: главным сочинением Меналая является « Сферика » в трёх книгах, сочинения «О вычислении хорд» в 6 книгах, «Начала геометрии» в 3 книгах, «Книга о треугольнике», «Книга о заходах знаков зодиака», «Книга о подразделении составных тел», посвящённая определению удельных весов тел, книга по гидростатике .
Труд « Сферика » стал вершиной достижений греков в сферической геометрии. Менелай первым ввел в геометрический обиход и исследовал простейший сферический многоугольник – треугольник. Он перенес на сферу евклидову теорию плоских треугольников и в числе прочего получил условие, при котором три точки на сторонах сферического треугольника или их продолжениях лежат на одной прямой. Интересно, что соответствующая теорема для плоскости в то время была уже широко известна, однако в историю геометрии она вошла именно как теорема Менелая . Биография ученого
Самым замечательным считается обыкновенная теорема Менелая Александрийского, которая прежде называлась правилом шести количеств. Содержание ее состоит в следующем. Если все стороны треугольника пересечь прямой, то произведение их трех отрезков, из числа не имеющих общих концов, равно произведению таких же трех остальных отрезков. Менелай выражал свою теорему в виде пропорции a 1 : b 1 = b 2 b 3 : a 2 a 3 , в которой буквы a 1 , a 2 и а 3 и, соответственно, буквы b 1 , b 2 и b 3 обозначают не имеющие общих концов отрезки трех сторон треугольника. Словесным выражением этой пропорции было предложение: а 1 находится к b 1 в таком же сложном отношении , в каком находятся b 2 к а 2 и b 3 к a 3 . Биография ученого
Пусть на сторонах AB , BC и продолжении стороны AC треугольника ABC взяты соответственно точки C 1 , A 1 , B 1 . Точки A 1 , B 1 , C 1 лежат на одной прямой тогда и только тогда, когда выполняется равенство: Теорема Менелая
Доказательство. Предположим, что точки A 1 , B 1 , C 1 принадлежат одной прямой a . Через вершину C треугольника ABC проведем прямую, параллельную a и обозначим через D точку её пересечения с AB . Из подобия треугольников ADC и AC 1 B 1 следует выполнимость равенства: Аналогично, из подобия треугольников BDC и BC 1 A 1 следует выполнимость равенства: Теорема Менелая Перемножая эти равенства, получим равенство: из которого следует требуемое равенство.
Докажем обратное . Пусть на сторонах AB , BC и продолжении стороны AC треугольника ABC взяты соответственно точки С 1 , А 1 , В 1 , для которых выполняется равенство . Предположим, что прямая A 1 B 1 пересекает прямую AB в некоторой точке С` . По доказанному, выполняется равенство: Учитывая первое равенство, получаем равенство : , из которого следует совпадение точек C` и C 1 и, значит, точки A 1 , B 1 , C 1 принадлежат одной прямой . Теорема Менелая
Теорема Менелая Если некоторая прямая пересекает стороны АВ и ВС треугольника АВС в точках X и Y соответственно, а продолжение стороны АС – в точке Z , то
Задача 1 . В треугольнике АВС на стороне ВС взята точка N так, что NC = 3 BN ;на продолжении стороны АС за точку А взята точка М так, что МА = АС . Прямая MN пересекает сторону АВ в точке F . Найдите отношение . Задачи на теорему Менелая
Решение. По условию задачи МА = AC , NC =3 BN . Пусть МА = АС = b , BN = k , NC = 3 k . Прямая MN пересекает две стороны треугольника АВС и продолжение третьей. По теореме Менелая : Ответ: 2 : 3 .
В треугольнике АВС точка М – середина стороны АС, точка Р лежит на стороне ВС. Отрезок АР пересекает ВМ в точке О. Оказалось, что ВО=ВР. Найти отношение ОМ:РС.
1 способ . Сделаем дополнительное построение: проведем через точку С прямую, параллельную ВМ; точку пересечения этой прямой с прямой АР обозначим через К. Рассмотрим треугольники ОВР и КСР. Углы ОРВ и КРС равны как вертикальные, углы ВОР и СКР равны как накрест лежащие при пересечении параллельных прямых ВМ и СК секущей АК. Поскольку по условию треугольник ОВР равнобедренный, угол ВОР = углу ОРВ, значит, и угол СРК= углу СКР. Значит, треугольник СКР – равнобедренный, т.е. СР=КС. Но, (например, по т. Фалеса) ОМ – средняя линия треугольника САК, она в 2 раза меньше, чем СК. Получаем, что ОМ:РС = ОМ:СК = 1:2 2 способ. По т. Менелая для треугольника МВС и прямой АР выполняется равенство: Тогда, используя условия АМ=МС и ВО=ВР получим, что МО:РС=1:2. Ответ: 1:2.
Задача 2 . Пусть AD — медиана треугольника АВС. На стороне AD взята точка К так, что АК : KD = 3:1. Прямая ВК разбивает треугольник АВС на два. Найдите отношение площадей этих треугольников.
Решение . Пусть AD = DC = a , KD = т; тогда АК = 3 т. Пусть Р — точка пересечения прямой ВК со стороной АС. Необходимо найти отношение . Так как треугольники АВР и РВС имеют равные высоты, проведенные из вершины В, то По теореме Менелая для треугольника ADC и секущей РВ имеем: Итак, Ответ : 3:2.
Задача 3. Дан параллелограмм ABCD . Точка M делит отрезок AD в отношении р , а точка N делит отрезок DC в отношении q . Прямые ВМ и AN пересекаются в точке S . Вычислите отношение AS : SN .
Решение. если MD = b , то AM = pb ; если NC = a , то ND = aq . Пусть В 1 – точка пересечения прямых ВМ и CD .
, тогда Прямая ВВ 1 пересекает две стороны и продолжение третьей треугольника AND . По теореме Менелая : Откуда Ответ :
Задача 4 . В треугольнике АВС точки К и L принадлежат соответственно сторонам АВ и ВС. АК : ВК = 1 : 2, CL : BL = 2 : 1. Q — точка пересечения отрезков AL и СК . S = 1. Найдите площадь треугольника АВС.
Решение . 1) В треугольнике МВС прямая AL пересекает две стороны и продолжение третьей стороны. По теореме Менелая : (1) В треугольнике АВМ прямая КС пересекает две стороны треугольника и продолжение третьей стороны. По теореме Менелая : (2) то есть MC = 4. p , AM = p . 2) Еще раз перепишем равенство (1): то есть 3) Треугольники BQC и МВС имеют общий угол, значит, Тогда = .
4) Треугольники АВС и МВС имеют равные высоты, проведенные из вершины В, значит, = = Ответ : 1,75.
Задача 5. Дано: окружность S касается окружностей S1 и S2 в точках А1 и А2. Доказать: что прямая А1А2 проходит через точку пересечения общих внутренних или внешних касательных к окружностям S1 и S2. S1 S2 A2 A1 S
Доказательство. Пусть О, О1 и О2 – центры окружностей S, S1 и S2; X – точка пересечения прямых О1О2 и А1А2. Применяя теорему Менелая к треугольнику ОО1О2 и точкам А1, А2 и Х, получаем: а значит, О1Х : О2Х = R1 : R2, где R1 и R2 – радиусы окружностей S1 и S2. Следовательно, Х – точка пересечения общих внешних или внутренних касательных к окружностям S1 и S2. X S A1 A2 O1 O2 S1 S2 О
Задача 6 . На стороне PQ треугольника PQR взята точка N , а на стороне Р R — точка L , причем NQ = LR . Точка пересечения отрезков QL и NR делит QL в отношении т : п , считая от точки Q . Найдите
Решение. По условию NQ = LR , Пусть NA = LR = а, QF = km , LF = kn . Прямая NR пересекает две стороны треугольника PQL и продолжение третьей. По теореме Менелая : Ответ : n : m .
Задача 7 . В треугольнике АВС, описанном около окружности, АВ = 8, ВС = 5, АС =4. А 1 и С 1 — точки касания, принадлежащие соответственно сторонам ВС и ВА. Р — точка пересечения отрезков АА 1 и СС 1. Точка Р лежит на биссектрисе ВВ 1 Найдите АР: РА 1 .
Решение . Точка касания окружности со стороной АС не совпадает с В 1 , так как треугольник АВС — разносторонний. Пусть С1В = х , тогда, используя свойство касательных, проведенных к окружности из одной точки, введем обозначения (см. рисунок) 8- x + 5 – x = 4, x Значит, В треугольнике АВА 1 , прямая С 1 С пересекает две его стороны и продолжение третьей стороны. По теореме Менелая : Ответ : 70 : 9 .
Задача 8. В треугольник АВС, описанном около окружности, АВ = 8, ВС = 12, АС = 9, А 1 и С 1 — точки касания, лежащие соответственно на сторонах ВС и АВ. Q — точка пересечения отрезков АА 1 и ВВ 1 . Q лежит на высоте ВВ 1 . Найдите отношение BQ : QB 1
Решение. Треугольник АВС — разносторонний, значит, точка В 1 не совпадает с точкой касания. 1) Пусть С 1 В = х , тогда, используя свойство касательных, проведенных к окружности из одной точки, введем обозначения (см. рисунок): (13 – х ) + (12 – х ) = 9, х = 8. Значит, С 1 В = 8, АС 1 = 5. 2) По формуле Герона: S = S = 3) Из треугольника ABB 1 (прямоугольного) по теореме Пифагора : 4) В треугольнике ABB 1 прямая CC 1 пересекает две его стороны и продолжение третьей. По теореме Менелая :
Задача 9 . Точки P и Q расположены на стороне ВС треугольника АВС так, что BP : PQ : QC = 1 : 2 : 3. Точка R делит сторону АС этого треугольника таким образом, что AR : RC = 1 : 2. Чему равно отношение площади четырехугольника PQST к площади треугольника АВС, где S и T — точки пересечения прямой В R с прямыми А Q и А P соответственно.
Решение. Обозначим BP = x , AR = y ; тогда PQ = 2x , QC = 3x , RC = 2y. Вычислим, какую часть площадь четырехугольника PQST составляет от площади треугольника APQ , а значит, и от площади треугольника ABC . Для этого нам понадобятся отношения, в которых точки S и T делят прямые AQ и AP соответственно. Применим к треугольнику ACQ и секущей SR теорему Менелая : Аналогично, применив теорему Менелая к треугольнику ACP и секущей TR , получим: Далее:
C другой стороны, применив лемму о площадях к треугольникам APQ и ABC , получим, что Ответ: .
Задача 10 . В треугольнике АВС длина высоты В D равна 6, длина медианы С E равна 5, расстояние от точки пересечения В D с С E до стороны АС равно 1. Найти длину стороны АВ.
Решение . Пусть точка О – точка пересечения прямых BD и CE . Расстояние от точки О до середины AC (равное по условию единице) есть длина отрезка OD. Итак, OD = 1 и OB = 5. Применим к треугольнику ABD и секущей OE теорему Менелая : Применив теперь теорему Менелая к треугольнику ACE и секущей OD , получим, что откуда OE = 2 CO , и с учетом OE + CO = CE = 5 получаем, что CO = . К прямоугольному треугольнику COD применим теорему Пифагора: Значит, AD = 4CD = . Наконец, рассмотрим прямоугольный треугольник ABD , в нем также воспользуемся теоремой Пифагора: Ответ: .
В треугольнике АВС отрезки АД и ВМ, проведенные из вершин А и В соответственно к сторонам ВС и ФС, пересекаясь в точке Р, делятся в отношении АР:РД =3:2 и ВР:РМ=4:5. В каком отношении точки Д и М делят стороны треугольника, считая от С? В треугольнике АВС точка Д делит сторону ВС в отношении ВД:ДС=3:4. Точка М делит сторону АС в отношении АМ:МС=2:5. Отрезки АД и ВМ пересекаются в точке К. Найдите площадь треугольника АКМ, если площадь треугольника ВКД равна 45. В треугольнике АВС точка К делит сторону АВ в отношении АК:КВ=1:2, а точка Р делит сторону ВС в отношении СР:РВ=2:1. Прямые АР и СК пересекаются в точке М. Найдите площадь треугольника АВС, если площадь треугольника ВМС равна 4. Дополнительные задачи
Прямая КР делит сторону АВ треугольника АВС в отношении АК:КВ=2:1, а сторону ВС — в отношении ВР:РС=3:1. Медиана ВВ1 пересекает прямую КР в точке М. При этом площадь четырехугольника В1МРС равна 17. Найдите площадь треугольника АВС. В треугольнике АВС на основании АС взяты точки Р и Т, так что АР
Видео:ОГЭ 23 КАК РЕШИТЬ ЗАДАЧУ НА ПОДОБНЫЕ ТРЕУГОЛЬНИКИСкачать

Подписи к слайдам:
Изучить теорему. Знать её применение. Уметь решать задачи на изученную теорему. Задачи:
В курсе геометрии 7-х –9-х классов были рассмотрены важные и интересные свойства геометрических фигур на плоскости. Но многие удивительные соотношения и изящные геометрические факты не вошли в основной курс. Из школьного курса нам известны теоремы о замечательных точках в треугольнике: три биссектрисы (медианы, высоты) пересекаются в одной точке. Эти свойства являются следствиями теоремы Менелая . Введение
Биография ученого Менела́й Александри́йский — древнегреческий математик и астроном, создатель системы геометрии и тригонометрии на сфере – первой неевклидовой геометрии. Время его жизни и деятельности определяется приведёнными в « Алмагесте » Птолемея двумя астрономическими наблюдениями, которые Менелай произвёл в Риме в первом году царствования Траяна, то есть в 98 году н. э. Его работы: главным сочинением Меналая является « Сферика » в трёх книгах, сочинения «О вычислении хорд» в 6 книгах, «Начала геометрии» в 3 книгах, «Книга о треугольнике», «Книга о заходах знаков зодиака», «Книга о подразделении составных тел», посвящённая определению удельных весов тел, книга по гидростатике .
Труд « Сферика » стал вершиной достижений греков в сферической геометрии. Менелай первым ввел в геометрический обиход и исследовал простейший сферический многоугольник – треугольник. Он перенес на сферу евклидову теорию плоских треугольников и в числе прочего получил условие, при котором три точки на сторонах сферического треугольника или их продолжениях лежат на одной прямой. Интересно, что соответствующая теорема для плоскости в то время была уже широко известна, однако в историю геометрии она вошла именно как теорема Менелая . Биография ученого
Самым замечательным считается обыкновенная теорема Менелая Александрийского, которая прежде называлась правилом шести количеств. Содержание ее состоит в следующем. Если все стороны треугольника пересечь прямой, то произведение их трех отрезков, из числа не имеющих общих концов, равно произведению таких же трех остальных отрезков. Менелай выражал свою теорему в виде пропорции a 1 : b 1 = b 2 b 3 : a 2 a 3 , в которой буквы a 1 , a 2 и а 3 и, соответственно, буквы b 1 , b 2 и b 3 обозначают не имеющие общих концов отрезки трех сторон треугольника. Словесным выражением этой пропорции было предложение: а 1 находится к b 1 в таком же сложном отношении , в каком находятся b 2 к а 2 и b 3 к a 3 . Биография ученого
Пусть на сторонах AB , BC и продолжении стороны AC треугольника ABC взяты соответственно точки C 1 , A 1 , B 1 . Точки A 1 , B 1 , C 1 лежат на одной прямой тогда и только тогда, когда выполняется равенство: Теорема Менелая
Доказательство. Предположим, что точки A 1 , B 1 , C 1 принадлежат одной прямой a . Через вершину C треугольника ABC проведем прямую, параллельную a и обозначим через D точку её пересечения с AB . Из подобия треугольников ADC и AC 1 B 1 следует выполнимость равенства: Аналогично, из подобия треугольников BDC и BC 1 A 1 следует выполнимость равенства: Теорема Менелая Перемножая эти равенства, получим равенство: из которого следует требуемое равенство.
Докажем обратное . Пусть на сторонах AB , BC и продолжении стороны AC треугольника ABC взяты соответственно точки С 1 , А 1 , В 1 , для которых выполняется равенство . Предположим, что прямая A 1 B 1 пересекает прямую AB в некоторой точке С` . По доказанному, выполняется равенство: Учитывая первое равенство, получаем равенство : , из которого следует совпадение точек C` и C 1 и, значит, точки A 1 , B 1 , C 1 принадлежат одной прямой . Теорема Менелая
Теорема Менелая Если некоторая прямая пересекает стороны АВ и ВС треугольника АВС в точках X и Y соответственно, а продолжение стороны АС – в точке Z , то
Задача 1 . В треугольнике АВС на стороне ВС взята точка N так, что NC = 3 BN ;на продолжении стороны АС за точку А взята точка М так, что МА = АС . Прямая MN пересекает сторону АВ в точке F . Найдите отношение . Задачи на теорему Менелая
Решение. По условию задачи МА = AC , NC =3 BN . Пусть МА = АС = b , BN = k , NC = 3 k . Прямая MN пересекает две стороны треугольника АВС и продолжение третьей. По теореме Менелая : Ответ: 2 : 3 .
В треугольнике АВС точка М – середина стороны АС, точка Р лежит на стороне ВС. Отрезок АР пересекает ВМ в точке О. Оказалось, что ВО=ВР. Найти отношение ОМ:РС.
1 способ . Сделаем дополнительное построение: проведем через точку С прямую, параллельную ВМ; точку пересечения этой прямой с прямой АР обозначим через К. Рассмотрим треугольники ОВР и КСР. Углы ОРВ и КРС равны как вертикальные, углы ВОР и СКР равны как накрест лежащие при пересечении параллельных прямых ВМ и СК секущей АК. Поскольку по условию треугольник ОВР равнобедренный, угол ВОР = углу ОРВ, значит, и угол СРК= углу СКР. Значит, треугольник СКР – равнобедренный, т.е. СР=КС. Но, (например, по т. Фалеса) ОМ – средняя линия треугольника САК, она в 2 раза меньше, чем СК. Получаем, что ОМ:РС = ОМ:СК = 1:2 2 способ. По т. Менелая для треугольника МВС и прямой АР выполняется равенство: Тогда, используя условия АМ=МС и ВО=ВР получим, что МО:РС=1:2. Ответ: 1:2.
Задача 2 . Пусть AD — медиана треугольника АВС. На стороне AD взята точка К так, что АК : KD = 3:1. Прямая ВК разбивает треугольник АВС на два. Найдите отношение площадей этих треугольников.
Решение . Пусть AD = DC = a , KD = т; тогда АК = 3 т. Пусть Р — точка пересечения прямой ВК со стороной АС. Необходимо найти отношение . Так как треугольники АВР и РВС имеют равные высоты, проведенные из вершины В, то По теореме Менелая для треугольника ADC и секущей РВ имеем: Итак, Ответ : 3:2.
Задача 3. Дан параллелограмм ABCD . Точка M делит отрезок AD в отношении р , а точка N делит отрезок DC в отношении q . Прямые ВМ и AN пересекаются в точке S . Вычислите отношение AS : SN .
Решение. если MD = b , то AM = pb ; если NC = a , то ND = aq . Пусть В 1 – точка пересечения прямых ВМ и CD .
, тогда Прямая ВВ 1 пересекает две стороны и продолжение третьей треугольника AND . По теореме Менелая : Откуда Ответ :
Задача 4 . В треугольнике АВС точки К и L принадлежат соответственно сторонам АВ и ВС. АК : ВК = 1 : 2, CL : BL = 2 : 1. Q — точка пересечения отрезков AL и СК . S = 1. Найдите площадь треугольника АВС.
Решение . 1) В треугольнике МВС прямая AL пересекает две стороны и продолжение третьей стороны. По теореме Менелая : (1) В треугольнике АВМ прямая КС пересекает две стороны треугольника и продолжение третьей стороны. По теореме Менелая : (2) то есть MC = 4. p , AM = p . 2) Еще раз перепишем равенство (1): то есть 3) Треугольники BQC и МВС имеют общий угол, значит, Тогда = .
4) Треугольники АВС и МВС имеют равные высоты, проведенные из вершины В, значит, = = Ответ : 1,75.
Задача 5. Дано: окружность S касается окружностей S1 и S2 в точках А1 и А2. Доказать: что прямая А1А2 проходит через точку пересечения общих внутренних или внешних касательных к окружностям S1 и S2. S1 S2 A2 A1 S
Доказательство. Пусть О, О1 и О2 – центры окружностей S, S1 и S2; X – точка пересечения прямых О1О2 и А1А2. Применяя теорему Менелая к треугольнику ОО1О2 и точкам А1, А2 и Х, получаем: а значит, О1Х : О2Х = R1 : R2, где R1 и R2 – радиусы окружностей S1 и S2. Следовательно, Х – точка пересечения общих внешних или внутренних касательных к окружностям S1 и S2. X S A1 A2 O1 O2 S1 S2 О
Задача 6 . На стороне PQ треугольника PQR взята точка N , а на стороне Р R — точка L , причем NQ = LR . Точка пересечения отрезков QL и NR делит QL в отношении т : п , считая от точки Q . Найдите
Решение. По условию NQ = LR , Пусть NA = LR = а, QF = km , LF = kn . Прямая NR пересекает две стороны треугольника PQL и продолжение третьей. По теореме Менелая : Ответ : n : m .
Задача 7 . В треугольнике АВС, описанном около окружности, АВ = 8, ВС = 5, АС =4. А 1 и С 1 — точки касания, принадлежащие соответственно сторонам ВС и ВА. Р — точка пересечения отрезков АА 1 и СС 1. Точка Р лежит на биссектрисе ВВ 1 Найдите АР: РА 1 .
Решение . Точка касания окружности со стороной АС не совпадает с В 1 , так как треугольник АВС — разносторонний. Пусть С1В = х , тогда, используя свойство касательных, проведенных к окружности из одной точки, введем обозначения (см. рисунок) 8- x + 5 – x = 4, x Значит, В треугольнике АВА 1 , прямая С 1 С пересекает две его стороны и продолжение третьей стороны. По теореме Менелая : Ответ : 70 : 9 .
Задача 8. В треугольник АВС, описанном около окружности, АВ = 8, ВС = 12, АС = 9, А 1 и С 1 — точки касания, лежащие соответственно на сторонах ВС и АВ. Q — точка пересечения отрезков АА 1 и ВВ 1 . Q лежит на высоте ВВ 1 . Найдите отношение BQ : QB 1
Решение. Треугольник АВС — разносторонний, значит, точка В 1 не совпадает с точкой касания. 1) Пусть С 1 В = х , тогда, используя свойство касательных, проведенных к окружности из одной точки, введем обозначения (см. рисунок): (13 – х ) + (12 – х ) = 9, х = 8. Значит, С 1 В = 8, АС 1 = 5. 2) По формуле Герона: S = S = 3) Из треугольника ABB 1 (прямоугольного) по теореме Пифагора : 4) В треугольнике ABB 1 прямая CC 1 пересекает две его стороны и продолжение третьей. По теореме Менелая :
Задача 9 . Точки P и Q расположены на стороне ВС треугольника АВС так, что BP : PQ : QC = 1 : 2 : 3. Точка R делит сторону АС этого треугольника таким образом, что AR : RC = 1 : 2. Чему равно отношение площади четырехугольника PQST к площади треугольника АВС, где S и T — точки пересечения прямой В R с прямыми А Q и А P соответственно.
Решение. Обозначим BP = x , AR = y ; тогда PQ = 2x , QC = 3x , RC = 2y. Вычислим, какую часть площадь четырехугольника PQST составляет от площади треугольника APQ , а значит, и от площади треугольника ABC . Для этого нам понадобятся отношения, в которых точки S и T делят прямые AQ и AP соответственно. Применим к треугольнику ACQ и секущей SR теорему Менелая : Аналогично, применив теорему Менелая к треугольнику ACP и секущей TR , получим: Далее:
C другой стороны, применив лемму о площадях к треугольникам APQ и ABC , получим, что Ответ: .
Задача 10 . В треугольнике АВС длина высоты В D равна 6, длина медианы С E равна 5, расстояние от точки пересечения В D с С E до стороны АС равно 1. Найти длину стороны АВ.
Решение . Пусть точка О – точка пересечения прямых BD и CE . Расстояние от точки О до середины AC (равное по условию единице) есть длина отрезка OD. Итак, OD = 1 и OB = 5. Применим к треугольнику ABD и секущей OE теорему Менелая : Применив теперь теорему Менелая к треугольнику ACE и секущей OD , получим, что откуда OE = 2 CO , и с учетом OE + CO = CE = 5 получаем, что CO = . К прямоугольному треугольнику COD применим теорему Пифагора: Значит, AD = 4CD = . Наконец, рассмотрим прямоугольный треугольник ABD , в нем также воспользуемся теоремой Пифагора: Ответ: .
В треугольнике АВС отрезки АД и ВМ, проведенные из вершин А и В соответственно к сторонам ВС и ФС, пересекаясь в точке Р, делятся в отношении АР:РД =3:2 и ВР:РМ=4:5. В каком отношении точки Д и М делят стороны треугольника, считая от С? В треугольнике АВС точка Д делит сторону ВС в отношении ВД:ДС=3:4. Точка М делит сторону АС в отношении АМ:МС=2:5. Отрезки АД и ВМ пересекаются в точке К. Найдите площадь треугольника АКМ, если площадь треугольника ВКД равна 45. В треугольнике АВС точка К делит сторону АВ в отношении АК:КВ=1:2, а точка Р делит сторону ВС в отношении СР:РВ=2:1. Прямые АР и СК пересекаются в точке М. Найдите площадь треугольника АВС, если площадь треугольника ВМС равна 4. Дополнительные задачи
Прямая КР делит сторону АВ треугольника АВС в отношении АК:КВ=2:1, а сторону ВС — в отношении ВР:РС=3:1. Медиана ВВ1 пересекает прямую КР в точке М. При этом площадь четырехугольника В1МРС равна 17. Найдите площадь треугольника АВС. В треугольнике АВС на основании АС взяты точки Р и Т, так что АР Мне нравится
Видео:№243. Через вершину С треугольника ABC проведена прямая, параллельная его биссектрисе АА1Скачать

В треугольнике ABM через вершину В проведена прямая D, параллельная стороне АM?
Математика | 5 — 9 классы
В треугольнике ABM через вершину В проведена прямая D, параллельная стороне АM.
Из вершин А и М проведены перпендикуляры АС и МD на прямую D.
Найдите площадь четырехугольника АСDМ, если площадь треугольника ABM равна 23 см в кв
Решение : здесь речь идёт о площади прямоугольника.
Видео:№26. Сторона АС треугольника ABC параллельна плоскости α, а стороныСкачать

Через середину К медианы ВМ треугольника АВС и вершину А проведена прямая, пересекающая сторону ВС в точке Р?
Через середину К медианы ВМ треугольника АВС и вершину А проведена прямая, пересекающая сторону ВС в точке Р.
Найдите отношение площади треугольника АВК к площади четырехугольника КРСМ.
ПОЖАЛУЙСТА ПОМОГИТЕ У МЕНЯ ЭКЗАМЕН.
Видео:№384. Через середину М стороны АВ треугольника ABC проведена прямая,Скачать

Через вершину с треугольника авс проведена прямая параллельная биссектрисе AM треугольника и пересекающая прямую AB в точке K?
Через вершину с треугольника авс проведена прямая параллельная биссектрисе AM треугольника и пересекающая прямую AB в точке K.
Найдите углы треугольника AKC если угол BAC = 70.
Видео:№194. Начертите треугольник. Через каждую вершину этого треугольника с помощью чертежногоСкачать

В равнобедренном прямоугольном треугольнике медиана, проведенная из вершины прямого угла, равна 5 см?
В равнобедренном прямоугольном треугольнике медиана, проведенная из вершины прямого угла, равна 5 см.
Найдите площадь треугольника.
Видео:№31. Плоскость α параллельна стороне ВС треугольника ABC и проходит черезСкачать

В равнобедренном треугольнике ABC с вершиной B проведена медиана AM к боковой стороне?
В равнобедренном треугольнике ABC с вершиной B проведена медиана AM к боковой стороне.
Найдите квадрат радиуса окружности, описанной около треугольника ABC, если радиусы окружностей, описанных около треугольников ABM и AMC, равны соответственно 36 и 9.
Видео:Задание 3 ЕГЭ по математике. Урок 41Скачать

Дан треугольник АВС?
Дан треугольник АВС.
Через вершину А проведите прямую, параллельную стороне ВС, через вершину В — прямую, параллельную стороне АС, через вершину С — прямую параллельную стороне АВ.
Сколько треугольников получилось?
Пожалуйста можно с рисунком!
Видео:Геометрия Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точкахСкачать

Через середину К медианы BM треугольника АБС и вершину А проведена прямая, пересекающая сторону ВС в точкее Р?
Через середину К медианы BM треугольника АБС и вершину А проведена прямая, пересекающая сторону ВС в точкее Р.
Найдите отношение площади треугольника АВК к площади четырехугольника КРСМ.
Видео:ОГЭ Р-2 номер 16Скачать

В треугольнике проведена высота из вершины прямого угла Докажите что данный треугольник из — за образовавшейся треугольника имеют соответственно равные углы?
В треугольнике проведена высота из вершины прямого угла Докажите что данный треугольник из — за образовавшейся треугольника имеют соответственно равные углы.
Видео:ОГЭ. Задание 24. Геометрическая задача на вычисление.Скачать

Постройте произвольный треугольник ?
Постройте произвольный треугольник .
Через его вершины проведите прямые , параллельные сторонам треугольника .
Сравните углы треугольника , образованного построенными прямыми , и треугольника.
Видео:№245. Через точку пересечения биссектрис ВВ1 и СС1 треугольника ABC проведена прямая, параллельнаяСкачать

В прямоугольнике ABCD проведена биссектриса AM?
В прямоугольнике ABCD проведена биссектриса AM.
Периметр прямоугольника равен 80 см.
Найдите сторону AD, если площадь треугольника ABM равна 162 см.
Видео:№563. Через точку М, взятую на медиане AD треугольника ABC, и вершину В проведена прямая,Скачать

Дан треугольник ABC?
Дан треугольник ABC.
Через вершину А проведите прямую, параллельную стороне ВС, через вершину В — прямую, параллельную стороне АС, через вершинуи С — прямую, параллельную стороне АВ.
Сколько попарно параллельных отрезков получилось?
Сколько треугольников получилось?
Вы находитесь на странице вопроса В треугольнике ABM через вершину В проведена прямая D, параллельная стороне АM? из категории Математика. Уровень сложности вопроса рассчитан на учащихся 5 — 9 классов. На странице можно узнать правильный ответ, сверить его со своим вариантом и обсудить возможные версии с другими пользователями сайта посредством обратной связи. Если ответ вызывает сомнения или покажется вам неполным, для проверки найдите ответы на аналогичные вопросы по теме в этой же категории, или создайте новый вопрос, используя ключевые слова: введите вопрос в поисковую строку, нажав кнопку в верхней части страницы.
📽️ Видео
Решаем геометрию ОГЭ по математике 2024! Задание №15.Скачать

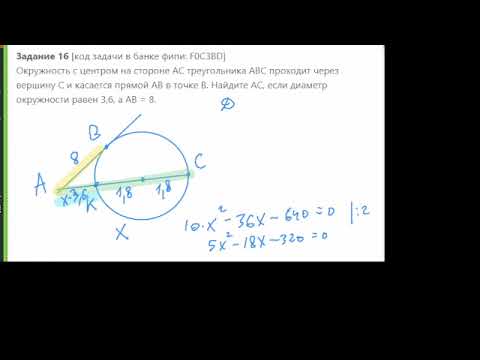
Окружность с центром на стороне AС треугольника ABC проходит через вершину С и касается прямой AB вСкачать
№196. Дан треугольник ABC. Сколько прямых, параллельных стороне АВ, можно провестиСкачать

Геометрия В треугольнике АВС проведена биссектриса АМ. Прямая, проходящая через вершину ВСкачать

№193. В треугольнике ABC ∠A=40°, ∠B=70°. Через вершину B проведена прямая BD так, что луч ВССкачать












