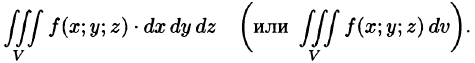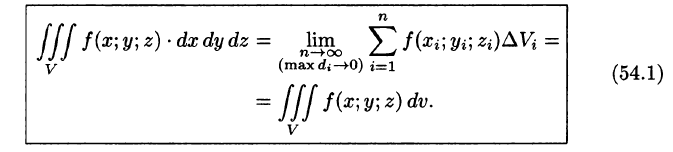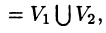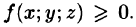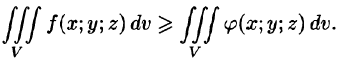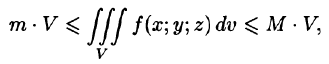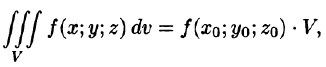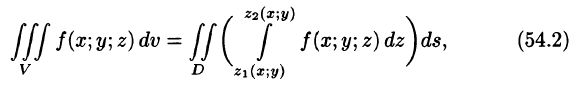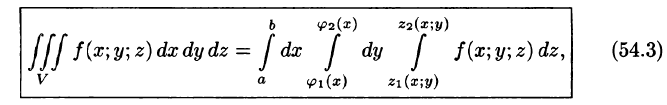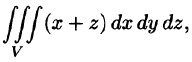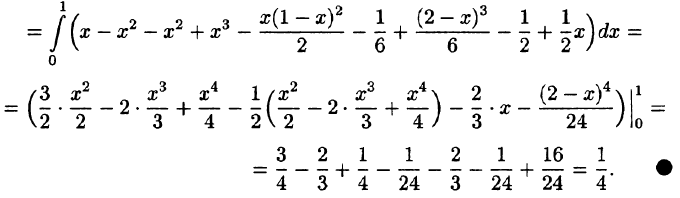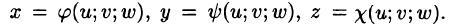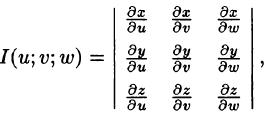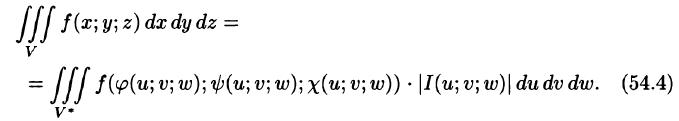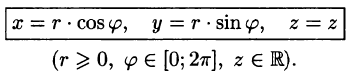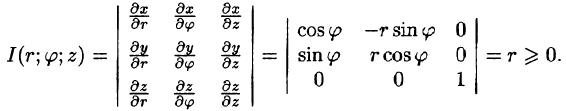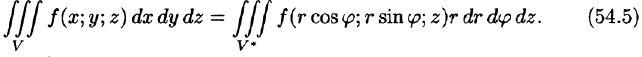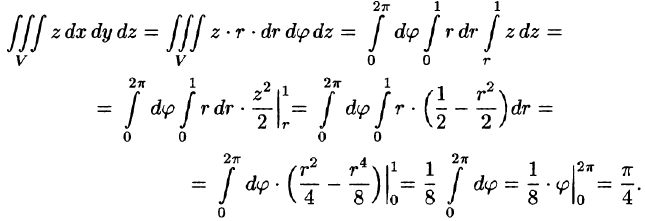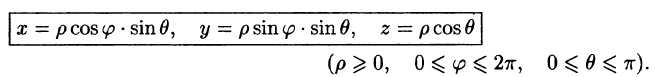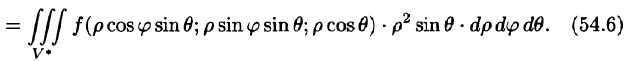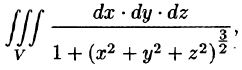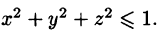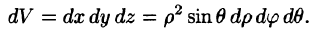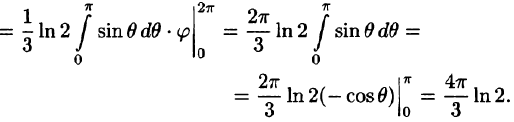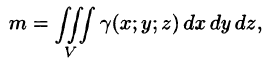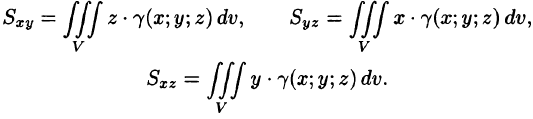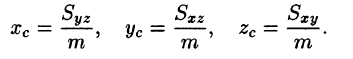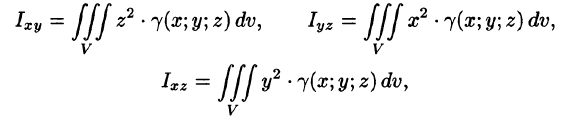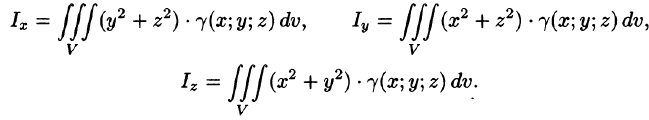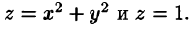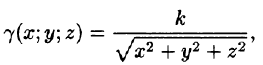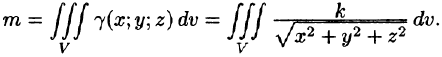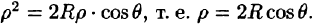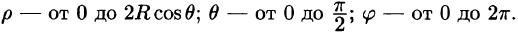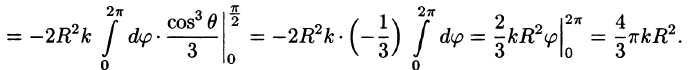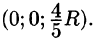Интеграл от вектора в сферических координатах

Обобщением определенного интеграла на случай функции трех переменных является так называемый «тройной интеграл».

Теория тройного интеграла аналогична теории двойного интеграла. Поэтому изложим ее в несколько сокращенном виде.

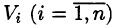
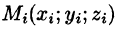
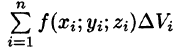
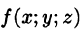
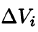
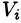
Пусть в замкнутой области V пространства Oxyz задана непрерывная функция и = f(x;y;z). Разбив область V сеткой поверхностей на п частей и выбрав в каждой из них произвольную точку , составим интегральную сумму для функции по области V (здесь — объем элементарной области ).

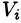
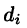
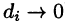
Если предел интегральной суммы существует при неограниченном увеличении числа п таким образом, что каждая «элементарная область» стягивается в точку (т. е. диаметр области стремится к нулю, т.е. ), то его называют тройным интегралом от функции и = f(х;у;z) по области V и обозначают

Таким образом, по определению, имеем:

Здесь dv = dx dy dz — элемент объема.

Теорема:

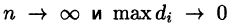
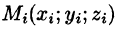
Если функция и = f(x;y,z) непрерывна в ограниченной замкнутой области V, то предел интегральной суммы (54.1) при существует и не зависит ни от способа разбиения области V на части, ни от выбора точек в них.
Тройной интеграл обладает теми же свойствами, что и двойной интеграл:

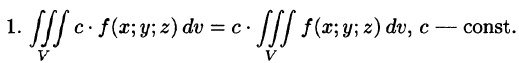
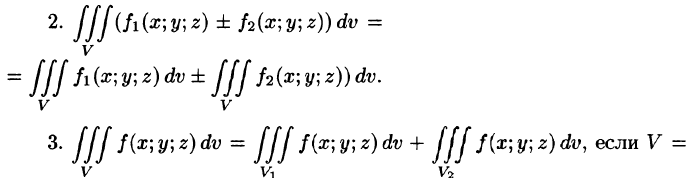
а пересечение 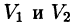состоит из границы, их разделяющей.
4. если в области V функция

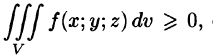
Если в области интегрирования 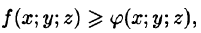то и

5.так как в случае любая интегральная сумма имеет вид и численно равна объему тела.

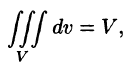
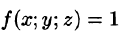
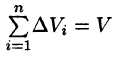
6. Оценка тройного интеграла:

где m и М — соответственно наименьшее и наибольшее значения функции f(x;y;z) в области V.

7. Теорема о среднем значении: если функция f(x; у, z) непрерывна в замкнутой области V, то в этой области существует такая точка 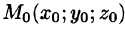, что

где V — объем тела.

Видео:Объем через тройной интеграл в сферической системе координатСкачать

Вычисление тройного интеграла в декартовых координатах

В декартовых координатах вычисление тройного интеграла сводится к последовательному вычислению трех определенных интегралов.

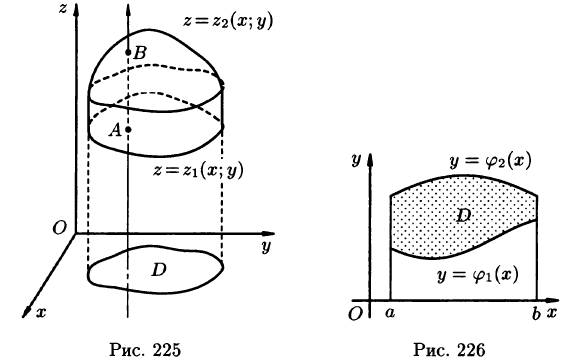
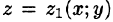
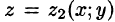
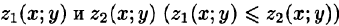
Пусть областью интегрирования V является тело, ограниченное снизу поверхностью , сверху — поверхностью , причем — непрерывные функции в замкнутой области D, являющейся проекцией тела на плоскость Оху (см. рис. 225). Будем считать область V — правильной в направлении оси Oz: любая прямая, параллельная оси Oz, пересекает границу области не более чем в двух точках. Тогда для любой непрерывной в области V функции f(х; у, z) имеет место формула

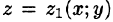
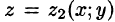
сводящая вычисление тройного интеграла к вычислению двойного интеграла от однократного (доказательство формулы (54.2) не приводим). При этом сначала вычисляется внутренний интеграл по переменной г при постоянных х и у в пределах изменения z. Нижней границей интеграла является аппликата точки А — точки входа прямой, параллельной оси Oz в область V, т. е. ; верхней границей — аппликата точки В — точки выхода прямой из области V, т. е. . Результат вычисления этого интеграла есть функция двух переменных: х и у.

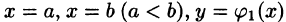
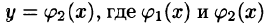
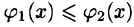
Если область D ограничена линиями и — непрерывные на отрезке [а, b] функции, причем (см. рис. 226), то, переходя от двойного интеграла по области D к повторному, получаем формулу

по которой вычисляется тройной интеграл в декартовых координатах.

Замечания:

1. Если область V более сложная, чем рассмотренная, то ее следует разбить на конечное число таких областей (правильных), к которым можно применить формулу (54.3).
2. Порядок интегрирования в формуле (54.3), при определенных условиях, может быть иным.

Пример:

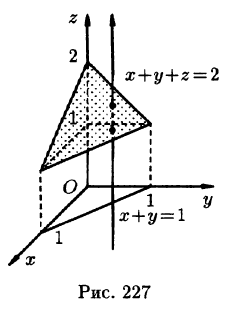
где V ограничена плоскостями х = 0, у =0, z = 1, x + y + z = 2 (рис. 227).

Решение:

Область V является правильной в направлении оси Oz (как, заметим, и в направлении осей Ох и Оу). Ее проекция на плоскость Оху является правильной в направлении оси Оу (и оси Ох). Согласно формуле (54.3), имеем:

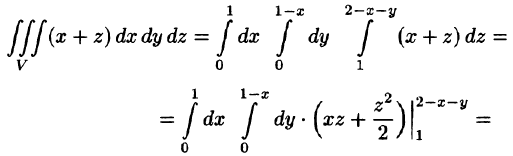
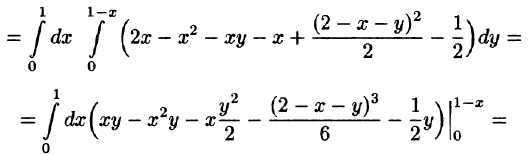
Замена переменных в тройном интеграле. Вычисление тройного интеграла в цилиндрических и сферических координатах

При вычислении тройного интеграла, как и двойного, часто применяется метод подстановки, т. е. совершается преобразование переменных.

Пусть совершена подстановка

Если эти функции имеют в некоторой области 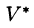пространства Ouvw непрерывные частные производные и отличный от нуля определитель

то справедлива формула замены переменных в тройном интеграле:

Здесь I(u; v;w) — определитель Якоби, или якобиан преобразования (примем без доказательства).

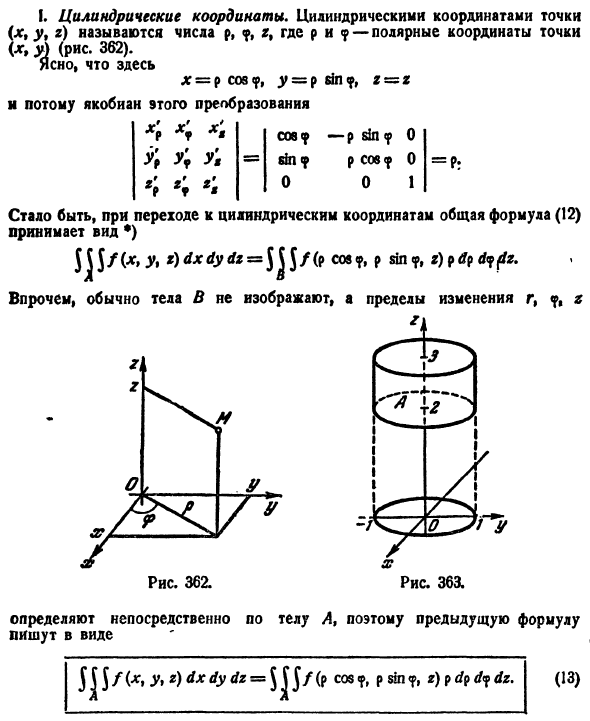
Для вычисления тройного интеграла часто используют так называемые цилиндрические координаты.

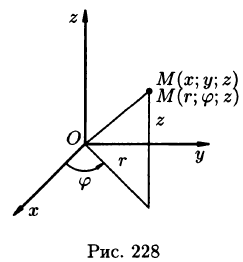
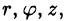
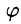
Положение точки М(х; у; z) в пространстве Oxyz можно определить заданием трех чисел где r — длина радиуса-вектора проекции точки М на плоскость Оху, — угол, образованный этим радиусом-вектором с осью Ox, z — аппликата точки М (см. рис. 228).

Эти три числа (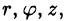) называются цилиндрическими координатами точки М.

Цилиндрические координаты точки связаны с ее декартовыми координатами следующими соотношениями:

Возьмем в качестве и, v, w цилиндрические координаты 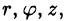и вычислим якобиан преобразования:

Формула замены переменных (54.4) принимает вид

Таким образом, вычисление тройного интеграла приводится к интегрированию по r, по 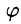и по z аналогично тому, как это делается в декартовых координатах.

Замечание:

К цилиндрическим координатам бывает удобно перейти в случае, если область интегрирования образована цилиндрической поверхностью.

Пример:

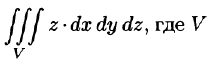
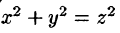
Вычислить — область, ограниченная верхней частью конуса и плоскостью z = 1.

Решение:

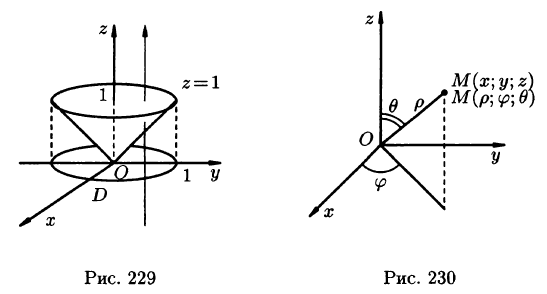
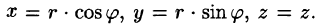
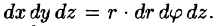
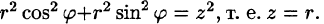
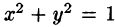
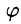
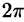
На рис. 229 изображена область интегрирования V. Вычислим интеграл путем перехода к цилиндрическим координатам: Здесь Уравнение конуса примет вид Уравнение окружности (границы области D) запишется так: r= 1. Новые переменные изменяются в следующих пределах: r— от 0 до 1, — от 0 до , a z — от r до 1 (прямая, параллельная оси Oz, пересекающая область D, входит в конус z =r и выходит из него на высоте z = 1).

Таким образом, согласно формуле (54.5), получаем:

Заметим, что, не переходя к цилиндрическим координатам, получим:

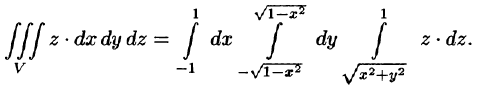
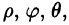
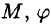
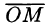
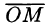
Сферическими координатами точки М(х; у; z) пространства Oxyz называется тройка чисел где р — длина радиуса-вектора точки — угол, образованный проекцией радиуса-вектора на плоскость Оху и осью Ох, в — угол отклонения радиуса-вектора от оси Oz (см. рис. 230).

Сферические координаты 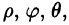связаны с декартовыми координатами х, у, z соотношениями:

В некоторых случаях вычисление тройного интеграла удобно производить, перейдя к сферическим координатам. Для этого нужно воспользоваться формулой замены переменных в тройном интеграле (54.4). Так как якобиан преобразования

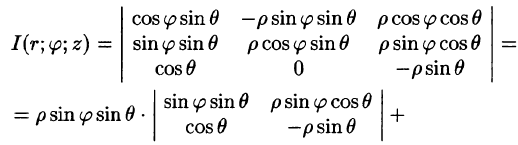
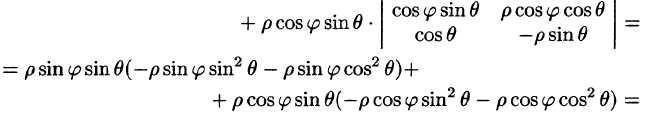
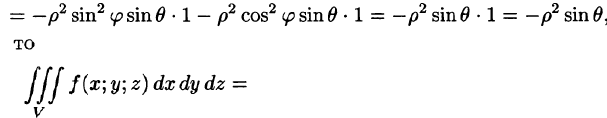
Замечание:

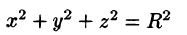
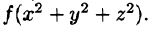
Переходить к сферическим координатам удобно, когда область интегрирования V есть шар (уравнение его границы в сферических координатах имеет вид р = R) или его часть, а также если подынтегральная функция имеет вид
Пример 54.3. Вычислить

где V — шар

Решение:

Вычислим интеграл путем перехода к сферическим координатам: 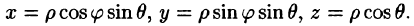Тогда

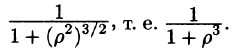
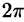
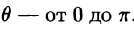
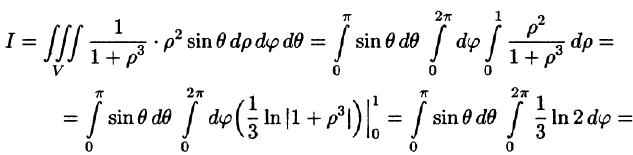
Граница области V — сфера и ее уравнение имеет вид р = 1, подынтегральная функция после замены переменных примет вид Новые переменные изменяются в следующих пределах: р —от 0 до 1, у — от 0 до , Таким образом, согласно формуле (54.6),

Видео:Двойной интеграл в полярных координатахСкачать

Некоторые приложения тройного интеграла Объем тела

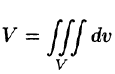
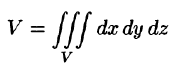
Объем области V выражается формулой или — в декартовых координатах,

Масса тела

Масса тела m при заданной объемной плотности 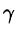вычисляется с помощью тройного интеграла как

где 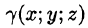— объемная плотность распределения массы в точке M<x;y;z).

Статические моменты

Моменты 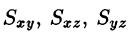тела относительно координатных плоскостей Оху, Oxz, Oyz вычисляются по формулам

Центр тяжести тела

Координаты центра тяжести тела V находятся по формулам

Моменты инерции тела

Моменты инерции тела относительно координатных плоскостей вычисляются по формулам

а моменты инерции относительно координатных осей:

Пример:

Найти объем тела, ограниченного поверхностями

Решение:

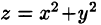
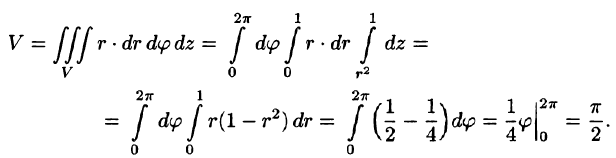
Данное тело ограничено сверху плоскостью z = 1, снизу — параболоидом (см. рис. 231). Объем тела находим, используя цилиндрические координаты:

Пример:

Найти массу шара 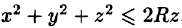, если плотность в каждой точке шара обратно пропорциональна расстоянию от нее до начала координат (дополнительно: найти координаты центра тяжести).

Решение:

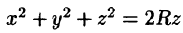
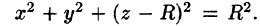
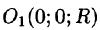
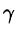
Уравнение сферы можно записать так: Центр шара расположен в точке (см. рис. 232). Пусть M(x;y;z) — произвольная точка шара. Тогда, по условию, плотность определяется формулой

где k — коэффициент пропорциональности, 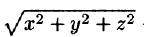— расстояние от точки М до начала координат.
Итак,

Вычислять интеграл будем в сферических координатах. Уравнение сферы 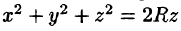примет вид

Поэтому сферические координаты будут изменяться в следующих пределах:

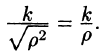
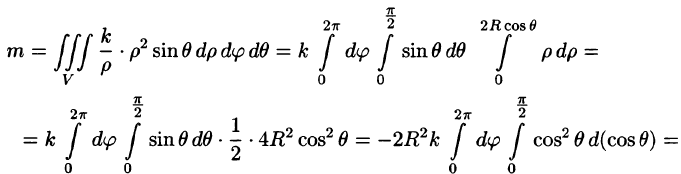
Подынтегральная функция примет вид Поэтому

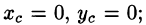
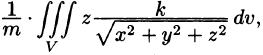
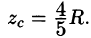
Из соображений симметрии следует, что вычислив интеграл найдем Итак, координаты центра тяжести

Видео:Сферические координатыСкачать

Тройной интеграл

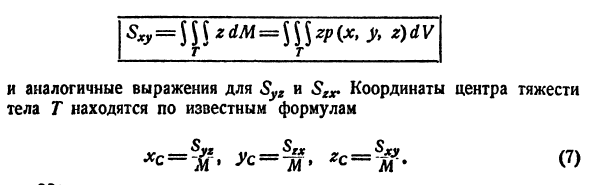
Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Видео:Математика Без Ху!ни. Полярные координаты. Построение графика функции.Скачать

Основные операции векторного анализа в криволинейных координатах

Содержание:

По этой ссылке вы найдёте полный курс лекций по математике:

Дифференциальные уравнения векторных линий Рассмотрим поле вектора Уравнения векторных линий в криволинейных координатах q, q2i g3 имеют вид В цилиндрических координатах в сферических координатах 14.2. Градиент в ортогональных координатах Пусть скалярное поле. Тогда Основные операции векторного анализа в криволинейных координатах Дифференциальные уравнения векторных линий радиент в ортогональных координатах Ротор в ортогональных координатах Дивергенция в ортогональных координатах.

Вычисление потенциала в криволинейных координатах Линейный интеграл и циркуляция в ортогональных криволинейных координатах Оператор Лапласа в ортогональных координатах В цилиндрических координатах в сферических координатах 14.3. Ротор в ортогональных координатах Рассмотрим векгорное поле и вычислим rot а. Имеем В цилиндрических координатах в сферических координатах 14.4. Дивергенция в ортогональных координатах Дивергенция div а векторного поля вычисляется по формуле.

В цилиндрических координатах или в сферических координатах

Применяя формулу (7) к единичным векторам получим Вычисление потока в криволинейных координатах Пусть S — часть координатной поверхности , ограниченная координатными линиями Тогда поток вектора через поверхность 5 в направлении вектора ei вычисляется по формуле Аналогично вычисляется поток через часть поверхности д2 = с, а также через часть поверхности д3 = с, где с = const. Пример I.

Найти поток П векторного поля через внешнюю сторону верхней полусферы 5 радиуса R с центром в начале координат. Ч Полусфера S есть часть юординатной поверхности г = const, а именно г = R. На полусфере 5 имеем , причем Учитывая, что в сферических коорои патах по формуле (8) найдем 14.6. Вычисление потенциала в криволинейных координатах Пусть в некоторой области О задано потенциальное векторное поле в области Для нахождения потенциала ) этого векторного поля запишем равенство в следующем виде:

Отсюда следует, что Интегрируя систему дифференциальных уравнений с частными производными (9), найдем искомый потенциал произвольная постоянная. В цилиндрических координатах система (9) принимает вид В сферических координатах система (9) имеет вид Пример 2. Найти потенциал векторного поля, заданного в цилиндрических координа тех Убедимся, что По формуле (5) л о лучим данное поле потенциально.

Искомый потенциал и = и(р, у, г) является решением следующей системы дифференциальных уравнений с частными производными (см. формулу (10)): Интегрированием по р из первого уравнения находим Дифференцируя соотношение (11) no р и используя второе уравнение, получим или откуда . Таким образом.

Возможно вам будут полезны данные страницы:

Дифференцируя это соотношение no z и используя тре тье уравнение, получим Линейный интеграл и циркуляция в ортогональных криволинейных координатах Пусть векторное поле определено и непрерывно в области Q изменения ортогональных криволинейных координат 4i, 42, 4з • Так как дифференциал радиус-вектора г любой точки M(qb 42, 43) G П выражается формулой то криволинейный интеграл вектора а(М) по ориентированной гладкой или кусочно-гладкой кривой L СП будет равен В частности, для цилиндрических координат ) будем иметь.

Отсюда по формуле (13) получим Аналогично для сферических координат будем иметь Отсюда по формуле (13) получим Основные операции векторного анализа в криволинейных координатах Дифференциальные уравнения векторных линий радиент в ортогональных координатах Ротор в ортогональных координатах Дивергенция в ортогональных координатах.

Вычисление потенциала в криволинейных координатах Линейный интеграл и циркуляция в ортогональных криволинейных координатах.

Оператор Лапласа в ортогональных координатах Если кривая L замкнута (начальная и конечная точки кривой L совпадают), то циркуляция Ц векторного поля а(М) в криволинейных координатах 4,, q2, 43 вычисляется по формуле (13), а в случае цилиндрических или сферических координат — по формулам (14) или (15) соответственно. Пример 3. Вычислить циркуляцию векторного поля, заданного в цилиндрических координатах по замкнутой кривой L, Координаты данного вектора равны соответственно Контур L представляет собой замкнутую кривую, расположенную в плоскости z = 0 (рис. 43).

Подставляя координаты данного вектора в формулу.(14), получим На кривой L имеем . Искомая циркуляция будет равна 14.8. Оператор Лапласа в ортогональных координатах Если скалярная функция, то Используя формулы (16) и (17), для оператора Лапласа Д получим следующее выражение В цилиндрических координатах получим В сферических координатах будем иметь Пример 4. Найти все решения уравнения Лапласа Аи = 0, зависящие только от расстояния г.

Так как искомое решение и должно зависеть только от расстояния точки М от начала координат г, т., то уравнение Лапласа Ди = 0 в сферических координатах будет иметь вид Отсюда так что где постоянные. Упражнения Найдите производную скалярного поля в точке по направлению кточке Найдите производную скалярного поля и(х, у, z) в точке Л#о(хо, Уо» *о) по направлению нормали к поверхности S, образующей острый угол с положительным направлением оси О г: 6.

Найдите производную скалярного поля в точке эллипса + = 1 по направлению внешней нормали к эллипсу в этой точке. 7. Найдите производную скалярного поля в точке по направлению окружности 8. Найдигеугол между градиентами функции и = arctg | в точках 9. Найдите производную плоского поля и вточке понаправле-нию, задаваемому вектором, лежащим в плоскости хОу и наклоненным под углом | коси Ох. Найдите векторные линии следующих векторных полей: 13.

через точку 14. Найдите векгорную линию поля а, проходящую через точку М(3,4, -1). 15. Вычислите поток векторного поля через верхнюю сторону круга, вырезаемого конусом х2 4- у2 = г2 из плоскости 16. Вычислите поток векторного поля к через треугольник ABC с вершинами в точках (нормаль образует с осью Oz острый угол). 17. Вычислите поток векторного поля а = xi + zk через боковую поверхность кругового цилиндра , ограниченную плоскостями z 18.

Вычислите поток векторного поля а = yzi — xj — yk через полную поверхность конуса х2 + у2 = z2, ограниченную плоскостью z Методом введения криволинейных координат на поверхности вычислите поток заданного векгора а через заданную поверхность S: 19. — внешняя сторона цилиндрической поверхности х2 + у2 = 9, ограниченной сферой Основные операции векторного анализа в криволинейных координатах Дифференциальные уравнения векторных линий радиент в ортогональных координатах Ротор в ортогональных координатах.

Дивергенция в ортогональных координатах

Вычисление потенциала в криволинейных координатах Линейный интеграл и циркуляция в ортогональных криволинейных координатах Оператор Лапласа в ортогональных координатах 20. — внешняя сторона части сферы , вырезанная конической поверхностью Вычислите поток векгорного поля а через замкнутую поверхность S (нормаль внешняя). Проверьте результат с помощью формулы Гаусса—Остроградского:

Достраивая подходящим образом заданные незамкнутые поверхности до замкнутых и пользуясь теоремой Гаусса—Остроградского, вычислите потоки векторных полей через указанные поверхности (к замкнутой поверхности берем внешнюю нормаль): Найдите работу силы F при перемещении вдольлинии L от точки М к точке N: Найдите циркуляцию векторного поля а вдоль замкнутого контура L (в направлении, соответствующем возрастанию параметра Вычислите циркуляцию векторного поля а по замкнутому контуру L.

Проверьте результат при помощи формулы Стокса: — линия пересечения плоскости с координатными плоскостями 38. Найдите дивергенцию векторного пол я а = (с, г), где с — постоянный вектор, . 39. При какой функции ip(z) дивергенция векгорного поля а =)k будет равна z? 40. Найдите , где г = 41. Найдите функцию tf>(r), для которой выполняется равенство 42. Какова должна быть функция /(х, z), чтобы ротор векгорного поля совпал с вектором Найдите ротор следующих векторов: Докажите, что следующие векторные поля являются потенциальными, и найдите их потенциалы: Ответы

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Видео:Пример решения тройного интеграла в сферических координатах - bezbotvyСкачать

Примеры применения цилиндрических и сферических координат

Примеры применения цилиндрических и сферических координат

1. Услуги проектирования
2. Тройной интеграл
3. Примеры применения цилиндрических и сферических координат

Видео:Тройной интеграл в сферических координатахСкачать

Примеры применения цилиндрических и сферических координат

Как и в случае перехода к полярным координатам в двойном интеграле, дать однозначный рецепт того, когда следует применять цилиндрические или сферические координаты, нельзя, это дело опыта. Можно попробовать применить цилиндрические координаты, если подынтегральная функция и/или уравнения поверхностей, ограничивающих объём $mathbf < textit > $, зависят от комбинации $mathbf < textit > ^ +mathbf < textit > ^ =mathbf < textit > ^ $; сферические — если эти уравнения зависят от $mathbf < textit > ^ +mathbf < textit > ^ +mathbf < textit > ^ =mathbf < textit > ^ $. Рассмотрим ряд примеров.

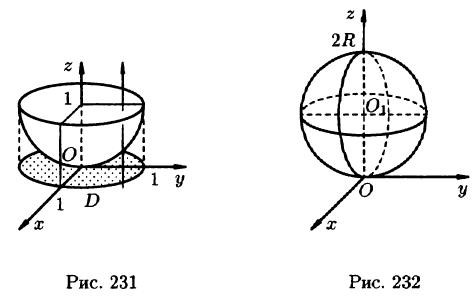
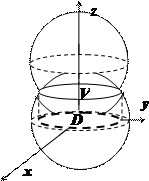
Найти объём $mathbf < textit > $ общей части двух шаров, ограниченных сферами

Решение:

Пересечение сфер находится на уровне $2Rz=R^2Rightarrow z=R/2$ и представляет собой круг радиуса $Rfrac $. Объём $mathbf < textit > $ограничен сверху поверхностью $z=sqrt $, снизу — поверхностью $z=R-sqrt $. Вычисления в декартовых координатах дают $V=iiintlimits_V =iiintlimits_V =intlimits_ < -Rfrac > ^ < Rfrac > < dxintlimits_ < -sqrt < frac R^2-x^2 > > ^ < sqrt < frac R^2-x^2 > > < dyintlimits_ < R-sqrt > ^ < sqrt > > > $ — достаточно громоздкие выкладки.

В цилиндрических координатах объём $mathbf < textit > $ ограничен сверху поверхностью $z=sqrt $, снизу — поверхностью $z=R-sqrt $, поэтому

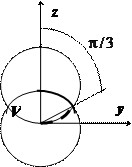
В сферических координатах уравнение нижней сферы принимает вид $r=R$, верхней — $r^2=2Rrcos theta Rightarrow r=2Rcos theta $, их пересечение соответствует значению $cos theta =1/2Rightarrow theta =pi /3$. В интервале $0leqslant theta leqslant pi /3 quad mathbf < textit > $ меняется от $0$ до $mathbf < textit > $, в интервале $pi /3leqslant theta leqslant pi /2 quad mathbf < textit > $ меняется от $0$ до $2Rcos theta $, поэтому

В этом примере трудоёмкость вычислений в цилиндрических и сферических координатах примерно одинакова.

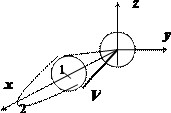
Решение:

Параболоид и конус пересекаются в плоскости $x=2-x^2Rightarrow x=1$ по кругу радиуса 1. Осью симметрии объёма $mathbf < textit > $ служит ось $mathbf < textit > $, поэтому цилиндрические координаты вводим формулами $x=x,quad y=rcos varphi ,quad z=rsin varphi ; quad I=iiintlimits_V =iiintlimits_V =intlimits_0^ < dvarphi intlimits_0^1 < rdrintlimits_r^ > > =$ $ =intlimits_0^ < dvarphi intlimits_0^1 < left. < frac >right|_r^ rdr > > +intlimits_0^ < (cos varphi +sin varphi )dvarphi intlimits_0^1 < left. x right|_r^ r^2dr > > =pi intlimits_0^1 < left( right)dr > =frac . $ Применение сферических координат в этом примере нецелесообразно .

Решение:

Здесь область интегрирования — шар радиуса 1/2, сдвинутый по оси $mathbf < textit > $ на 1/2 единицы, подынтегральная функция зависит от выражения $mathbf < textit > ^ +mathbf < textit > ^ +mathbf < textit > ^ $, поэтому применим сферические координаты. Уравнение сферы $x^2+y^2+z^2=zRightarrow r^2=rcos theta Rightarrow r=cos theta left( right)$ , поэтому $I=iiintlimits_V < sqrt dxdydz > =iiintlimits_V =intlimits_0^ < dvarphi intlimits_0^ intlimits_0^ > =frac intlimits_0^ < left. right|_0^ sin theta dtheta > = \ =frac intlimits_0^ =-frac left. right|_0^ =frac $.

Вычислить объём тела, ограниченного поверхностью $left( right)^ =a^3z,;a=const>0$

Решение:

Здесь тоже для того, чтобы понять, как устроено тело, и найти его объём, надо перейти к сферическим координатам < на это указывает комбинация $mathbf < textit > ^ +mathbf < textit > ^ +mathbf < textit > ^ =mathbf < textit > ^ )$. Уравнение поверхности $left( right)^ =a^3zRightarrow r^4=a^3rcos vartheta Rightarrow r=asqrt[3] ;left( right)$. По этому уравнению поверхность построить уже можно; отсутствие координаты $varphi $ в уравнении показывает, что это — тело вращения вокруг оси $mathbf < textit > $. Находим объём: $ V=iiintlimits_V =intlimits_0^ < dvarphi intlimits_0^ > theta dtheta intlimits_0^ < asqrt[3] > =frac intlimits_0^ < left. right|_0^ < asqrt[3] > sin theta dtheta = > $ $ =frac intlimits_0^ frac . $

Вычислить интеграл $iiintlimits_U < left( < + 2 + >right)dxdydz > ,$ где область (U) ограничена поверхностью ( + le 1) и плоскостями (z = 0,) (z = 1).

Решение:

Данный интеграл удобно вычислить в цилиндрических координатах. Проекция области интегрирования на плоскость (Oxy) представляет собой круг ( + le 1) или (0 le rho le 1).

Заметим, что подынтегральное выражение записывается в виде $ < left( < + 2 + >right) > = < < left( < + >right)^2 > > = < < left( < >right)^2 > = > $

Тогда интеграл будет равен $I = intlimits_0^ intlimits_0^1 < rho drho > intlimits_0^1 .$

Здесь во втором интеграле добавлен множитель (rho) якобиан преобразования декартовых координат в цилиндрические. Все три интеграла по каждой из переменной не зависят друг от друга.

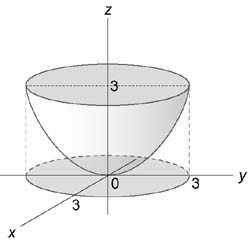
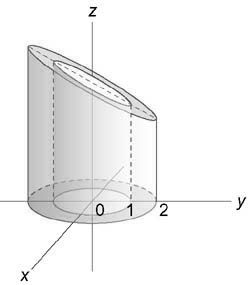
Вычислить интеграл $iiintlimits_U < left( < + >right)dxdydz > ,$ где область (U) ограничена поверхностями ( + = 3z,) (z = 3)

Решение:

Область интегрирования изображена на рисунке

Для вычисления интеграла перейдем к цилиндрическим координатам: $ ;; ;; $ Дифференциал при этом равен $dxdydz = rho drho dvarphi dz;;left( < rho — text >right).$

Уравнение параболической поверхности принимает вид: $ varphi + varphi = 3z;;text ;; = 3z.$ Проекция области интегрирования (U) на плоскость (Oxy) представляет собой окружность ( + le 9) радиусом (rho = 3).

Координата (rho) изменяется в пределах от (0) до (3,) угол (varphi) от (0) до (2pi) и координата (z) от (largefrac < < > > normalsize) до (3.)

Используя цилиндрические координаты, найти значение интеграла $ I = intlimits_ ^2 intlimits_ < — sqrt < 4 — > > ^ < sqrt < 4 — > > intlimits_0^ < 4 — — > < dz > $

Решение:

Область интегрирования (U) изображена на рисунке:

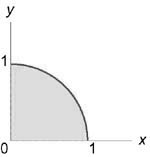
Ее проекция на плоскость (Oxy) представляет собой круг ( + = ):

Новые переменные в цилиндрических координатах будут изменяться в пределах $ ;; ;; < 0 le z le 4 — . > $

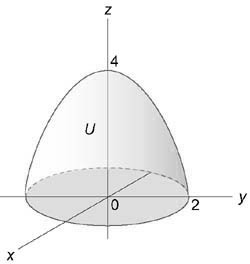
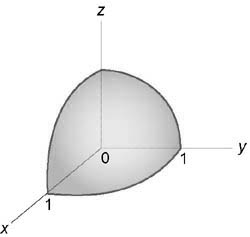
Вычислить интеграл, используя цилиндрические координаты: $iiintlimits_U < sqrt < + > dxdydz > .$ Область (U) ограничена параболоидом (z = 4 — — ,) цилиндром ( + = 4) и плоскостями (y = 0,) (z = 0)

Решение:

Изобразив схематически область интегрирования (U,) находим, что ее проекция на плоскость (Oxy) представляет собой полукруг радиусом (rho = 2).

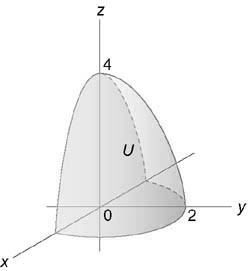
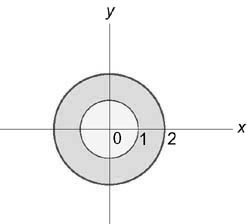
Найти интеграл $iiintlimits_U ,$ где область (U) ограничена плоскостями (z = x + 1,) (z = 0) и цилиндрическими поверхностями ( + = 1,) ( + = 4)

Решение:

Вычислим данный интеграл в цилиндрических координатах. Из условия $0 le z le x + 1$ следует, что $0 le z le rho cos varphi + 1.$ Область интегрирования в плоскости (Oxy) представляет собой кольцо, ограниченное окружностями ( + = 1) и ( + = 4)

Следовательно, переменные (rho) и (varphi) изменяются в интервале $1 le rho le 2,;;0 le varphi le 2pi .$

Этот результат закономерен, поскольку область (U) симметрична относительно плоскости (Oxz,) а подынтегральная функция является четной.

Найти интеграл (iiintlimits_U < sqrt < + + > dxdydz > ,) где область интегрирования (U) шар, заданный уравнением ( < + + > = 25.)

Решение:

Поскольку область (U) представляет собой шар, и к тому же подынтегральное выражение является функцией, зависящей от $fleft( < + + >right),$ то перейдем к сферическим координатам.

Вычислить интеграл $iiintlimits_U < < e^ < < < left( < + + >right) > ^ < frac > > > > dxdydz > ,$ где область (U) представляет собой единичный шар ( < + + > le 1.)

Решение:

Центр данного шара расположен в начале координат. Следовательно, в сферических координатах область интегрирования (U) описывается неравенствами $ ;; ;; $

Как видно, тройной интеграл вырождается в произведение трех однократных интегралов, каждый из которых вычисляется независимо. В результате находим $ < I = intlimits_0^ intlimits_0^1 < < e^ < > > drho > intlimits_0^pi > = < left[ < left. varphi right|_0^ >right] cdot intlimits_0^1 < left( < < e^ < > > cdot frac d >right) > cdot left[ < left. < left( right) >right|_0^pi >right] > = < 2pi cdot frac left[ < left. < left( < < e^ < > > >right) >right|_ < = 0 > ^ < = 1 > >right] cdot left( right) > = < frac < > cdot left( right) cdot 2 > = < frac < > left( right). > $

Вычислить интеграл (iiintlimits_U ,) где область (U) представляет собой часть шара ( + + le ,) расположенную в первом октанте (x ge 0, y ge 0, z ge 0.)

Решение:

Найти тройной интеграл $iiintlimits_U < left( < frac < < > > < < > > + frac < < > > < < > > + frac < < > > < < > > >right)dxdydz > ,$ где область (U) ограничена эллипсоидом $ < frac < < > > < < > > + frac < < > > < < > > + frac < < > > < < > > > = 1.$

Решение:

Для вычисления интеграла перейдем к обобщенным сферическим координатам путем следующей замены переменных: $ ;; ;; $ Модуль якобиана данного преобразования равен (left| I right| = abc sin theta .) Поэтому для дифференциалов справедливо соотношение $dxdydz = abc sin theta drho dvarphi dtheta .$ В новых координатах интеграл принимает вид: $ < I = iiintlimits_U < left( < frac < < > > < < > > + frac < < > > < < > > + frac < < > > < < > > >right)dxdydz > > = < iiintlimits_ < left[ < frac < < < < left( right) > ^2 > > > < < > > + frac < < < < left( right) > ^2 > > > < < > > + frac < < < < left( right) > ^2 > > > < < > > >right]abc sin theta drho dvarphi dtheta > > = \ = < iiintlimits_ < left[ < < ^2 > varphi , < ^2 > theta + varphi , < ^2 > theta + < ^2 > theta >right]abc sin theta drho dvarphi dtheta > > = \ = < iiintlimits_ < left[ < < ^2 > theta underbrace < left( < < ^2 > varphi + varphi >right) > _1 + < ^2 > theta >right]abc sin theta drho dvarphi dtheta > > = \ = < iiintlimits_ < underbrace < left( < theta + < ^2 > theta >right) > _1abc sin theta drho dvarphi dtheta > > = < abciiintlimits_ < sin theta drho dvarphi dtheta > . > $

Вычислить интеграл $intlimits_0^1 intlimits_0^ < sqrt < 1 — > > intlimits_0^ < sqrt < 1 — — > > < < < left( < + + >right) > ^2 > dz > ,$ используя сферические координаты.

Решение:

Область интегрирования представляет собой часть шара, расположенная в первом октанте и, следовательно, ограничена неравенствами $ ;; < 0 le varphi le frac , > ;; < 0 le theta le frac . > $

Далее:

Формула Гаусса — Остроградского

Класс $S$. Теорема о замкнyтости класса $S$

Поток векторного поля через поверхность

Класс M. Теорема о замкнутости класса M

Несобственные интегралы по неограниченной области

Логические операции над высказываниями

Специальные векторные поля

Вычисление объёмов

Вычисление площади поверхности

Выражение площади плоской области через криволинейный интеграл

Вычисление криволинейного интеграла второго рода. Примеры.

Вычисление поверхностного интеграла первого рода

Теорема о предполных классах

Равносильные формулы алгебры высказываний

Огравление $Rightarrow $

🎦 Видео

Площадь фигуры через двойной интеграл в полярных координатахСкачать

Тройной интеграл в сферических координатах. Вычисление тройного интеграла в сферических координатах.Скачать

Цилиндрическая система координат(ЦСК).Тройной интегралСкачать

Вычислить двойной интеграл, перейдя к полярным координатамСкачать

Перейти к полярным координатам в двойном интегралеСкачать

Тройной интеграл. Тройной интеграл в сферических координатахСкачать

Двойные интегралы в полярных координатахСкачать

Двойной интеграл (ч.25). Вычисление в полярных координатах. Высшая математика.Скачать

ТРОЙНОЙ ИНТЕГРАЛ. СФЕРИЧЕСКИЕ КООРДИНАТЫСкачать

Как использовать интеграл в обычной жизни. Математик МГУ и Савватеев #shortsСкачать

Объем параболоида: тройной интеграл в цилиндрической системе координатСкачать

Тройной интеграл в сферических координатахСкачать

§56 Сферическая система координатСкачать