Скачать
презентацию
Задача №93. N. ? Дано: a || b. a. М. b. MN ? a = M. Определить взаимное расположение прямых MN u b. Скрещивающиеся.
Слайд 12 из презентации «Взаимное расположение прямых в пространстве» к урокам геометрии на тему «Стереометрия»
Размеры: 960 х 720 пикселей, формат: jpg. Чтобы бесплатно скачать слайд для использования на уроке геометрии, щёлкните на изображении правой кнопкой мышки и нажмите «Сохранить изображение как. ». Скачать всю презентацию «Взаимное расположение прямых в пространстве.ppt» можно в zip-архиве размером 137 КБ.
- Стереометрия
- Материал к уроку геометрии в 10 классе «Скрещивающиеся прямые. Угол между прямыми»
- Взаимное расположение прямых в пространстве
- Но надо жить без самозванства,
- Дан куб АВСDA1B1C1D1 Выясните взаимное расположение прямых
- Теорема. Признак скрещивающихся прямых
- Алгоритм доказательства с использованием признака скрещивающихся прямых
- Куб ABCDA1B1C1D1
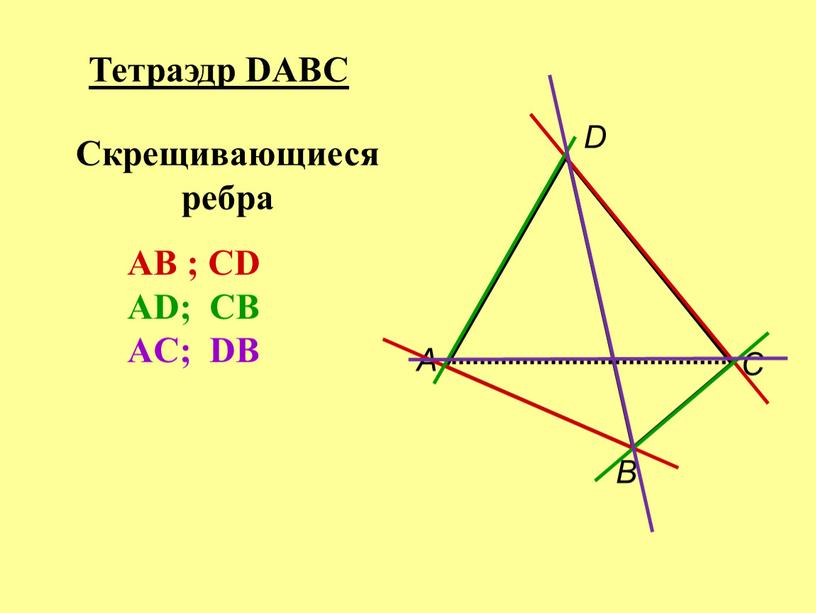
- А В С D Тетраэдр DABC Скрещивающиеся ребра
- Задача №34. А В С D M N P Р1 К
- Задача №34 А В С D M N P К Дано:
- Задача №93 α a b М N Дано: a || b
- Определить взаимное расположение прямых
- Можно ли через одну из скрещивающихся прямых провести плоскость?
- О существовании параллельных плоскостей, проходящих через скрещивающиеся прямые
- Теорема: Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна
- Теорема: Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна
- Презентация по геометрии 10 класс на тему
- «Календарь счастливой жизни: инструменты и механизм работы для достижения своих целей»
- «Управление общеобразовательной организацией: новые тенденции и современные технологии»
- Дистанционное обучение как современный формат преподавания
- Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Математика: теория и методика преподавания в образовательной организации
- Оставьте свой комментарий
- Подарочные сертификаты
Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Стереометрия
«Сравнение отрезков» — B. ©Максимовская М.А., 2009 год. Сравнение отрезков и углов. Определение. A. Сравнение отрезков. C.
«Многообразия» — Рис. 1. 10. 26. Рис. 5. Рис. 11. Рис. 10. 14. 5. Рис. 2. Рис. 14. 9. t=0. Рис. 18. Трехмерные многообразия. 18. Sylvia Nasar and David Cruber. Рис.8. В нем вводится естественная метрика Сасаки. 19. Рис. 21. Например, поверхность куба гомеоморфна сфере (рис.2). 29. Рис. 19. 17. Рис. 17. 16. Однородные трехмерные геометрии.
«Учебник по геометрии» — Уравнение прямой 73*. Гомотетия 48*. Многогранники в задачах оптимизации 58*. Полуправильные многогранники 29*. Симметрия пространственных фигур 41. Прямоугольные треугольники 49 15. Теорема Фалеса ГЛАВА VI. Площадь многоугольника 62. Полярные координаты ГЛАВА XII. Эллипс 23*. Координаты вектора 53.
«Измерение отрезков» — Для измерения более мелких длин единицей измерения можно считать сантиметр, миллиметр и т. д. К измерительным приборам могут относиться линейка, рулетка и т. п. Единицы измерения. План урока: Длина отрезка Единицы измерения. Измерительные инструменты. Отсюда можно сделать вывод, что равные отрезки имеют равные длины.
«Взаимное расположение прямых в пространстве» — ?. a ? b. Признак скрещивающихся прямых. a. Ввести определение скрещивающихся прямых. Почему? Цели урока: Дано: АВ ?, СD ? ? = С, С АВ. Являются ли параллельными прямые АА1 и DD1; АА1 и СС1 ? . Расположение прямых в пространстве:
«Геометрия это наука» — Объяснение устройства мира пифагорейцы тесно связывали с геометрией. Евклид – древнегреческий ученый, живший около 300 г. до нашей эры. Что означает слово «планиметрия»? Что означает слово «стереометрия»? Евклид. Из каких двух основных разделов состоит геометрия? Где зародилась геометрия? В стереометрии изучаются неплоские фигуры, т.е. не лежащие в одной плоскости.
Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Материал к уроку геометрии в 10 классе «Скрещивающиеся прямые. Угол между прямыми»
Видео:Взаимное расположение прямых в пространстве. 10 класс.Скачать

Взаимное расположение прямых в пространстве
Взаимное расположение прямых в пространстве
Скрещивающиеся прямые
Угол между прямыми
Видео:Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

Но надо жить без самозванства,
Но надо жить без самозванства,
Так жить, чтобы в конце концов
Привлечь к себе любовь
пространства,
Услышать будущего зов.
Б. Л. Пастернак
Видео:10 класс, 7 урок, Скрещивающиеся прямыеСкачать

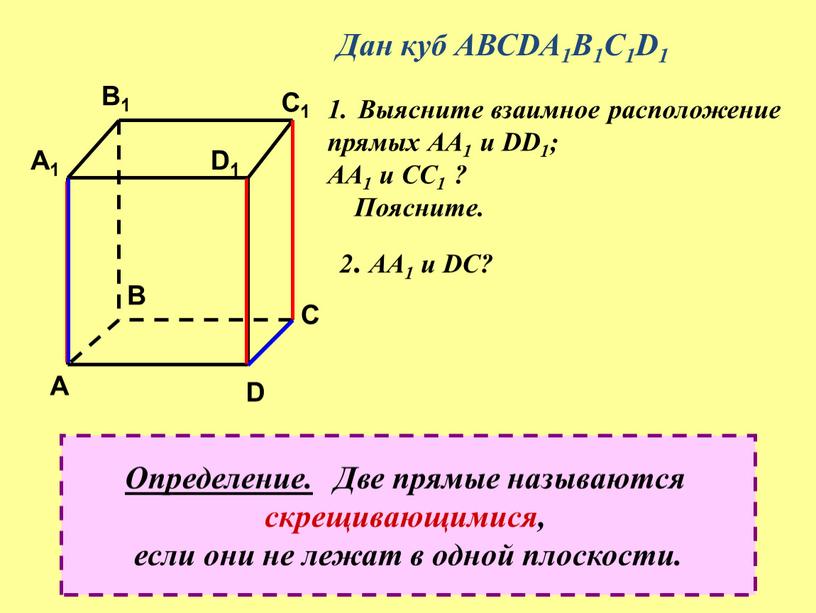
Дан куб АВСDA1B1C1D1 Выясните взаимное расположение прямых
Дан куб АВСDA1B1C1D1
Выясните взаимное расположение
прямых АА1 и DD1;
АА1 и СС1 ?
Поясните.
Определение. Две прямые называются
скрещивающимися,
если они не лежат в одной плоскости.
Видео:Прямые m и n параллельны. Найдите ∠3, если ∠1=24°, ∠2=90° | ОГЭ 2017 | ЗАДАНИЕ 9 | ШКОЛА ПИФАГОРАСкачать

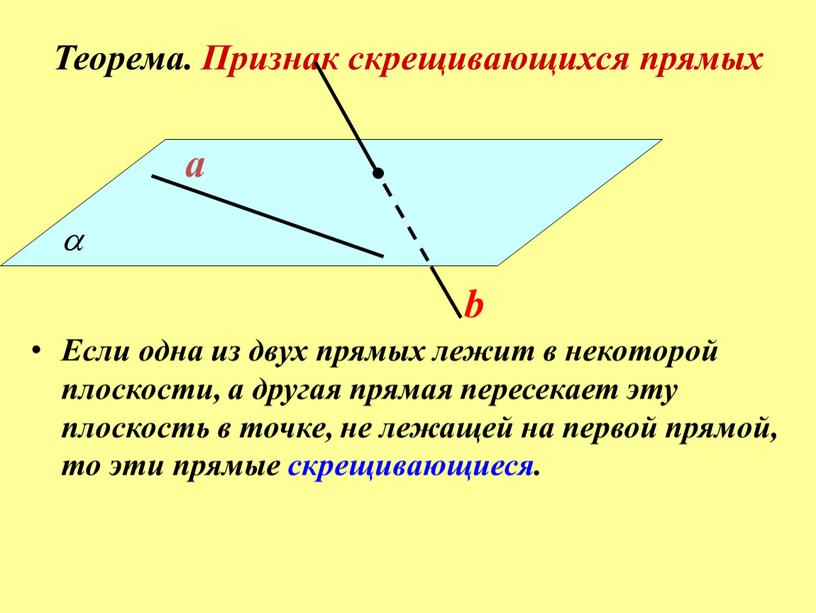
Теорема. Признак скрещивающихся прямых
Теорема. Признак скрещивающихся прямых
Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся.
Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

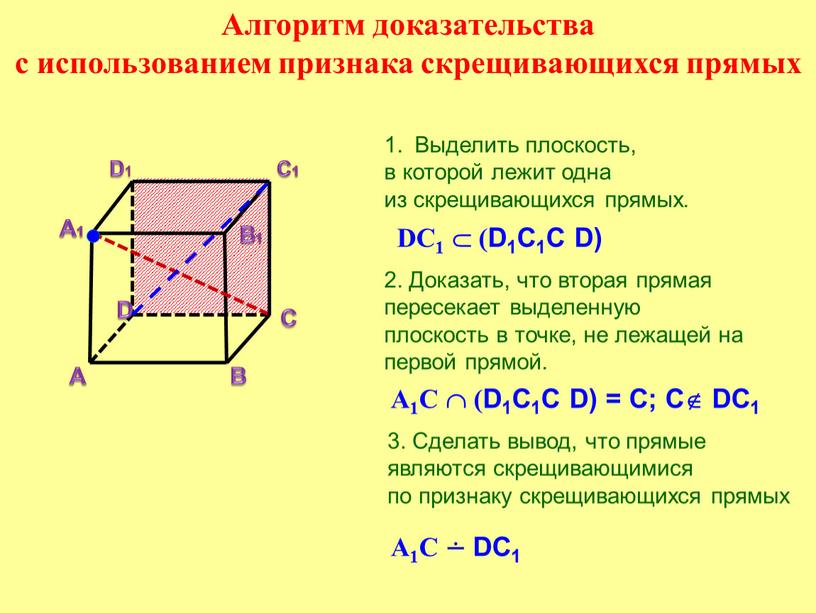
Алгоритм доказательства с использованием признака скрещивающихся прямых
Алгоритм доказательства
с использованием признака скрещивающихся прямых
Выделить плоскость,
в которой лежит одна
из скрещивающихся прямых.
2. Доказать, что вторая прямая
пересекает выделенную
плоскость в точке, не лежащей на
первой прямой.
3. Сделать вывод, что прямые
являются скрещивающимися
по признаку скрещивающихся прямых
А1C (D1C1С D) = С; С DC1
Видео:Параллельность прямой и плоскости. 10 класс.Скачать

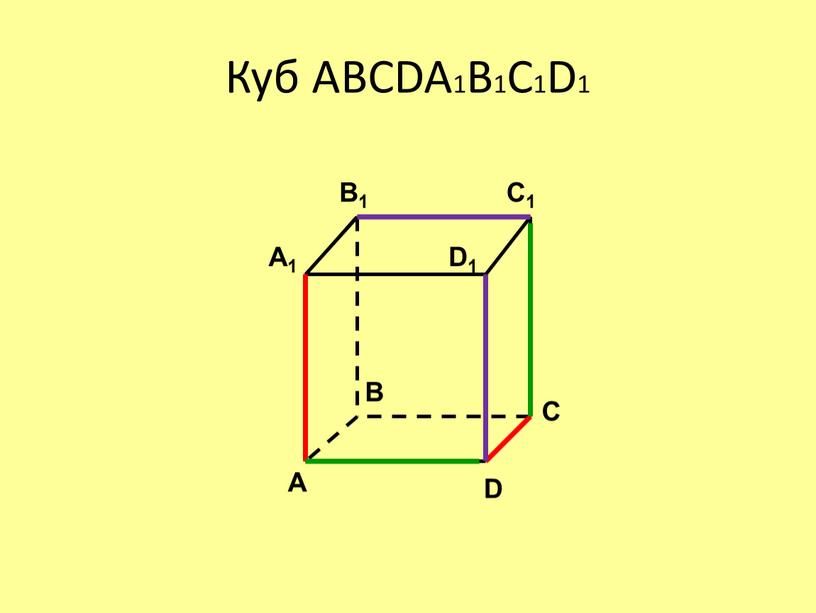
Куб ABCDA1B1C1D1
Видео:Взаимное расположение прямых в пространстве. Видеоурок 3. Геометрия 10 классСкачать

А В С D Тетраэдр DABC Скрещивающиеся ребра
AB ; CD
AD; CB
AC; DB
Видео:Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

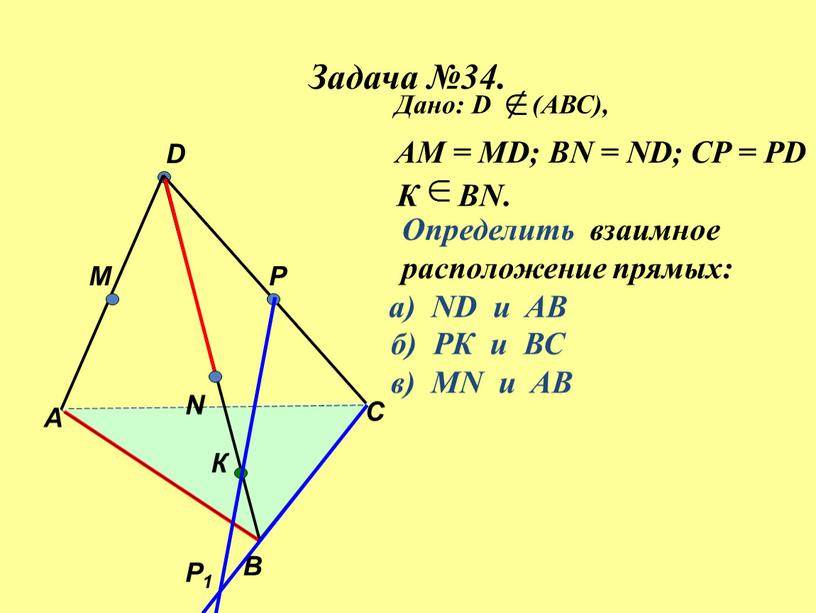
Задача №34. А В С D M N P Р1 К
АМ = МD; ВN = ND; CP = PD
Определить взаимное
расположение прямых:
Видео:Стереометрия 10 класс. Часть 2 | Математика | TutorOnlineСкачать

Задача №34 А В С D M N P К Дано:
АМ = МD; ВN = ND; CP = PD
Определить взаимное
расположение прямых:
Видео:10 класс, 14 урок, Задачи на построение сеченийСкачать

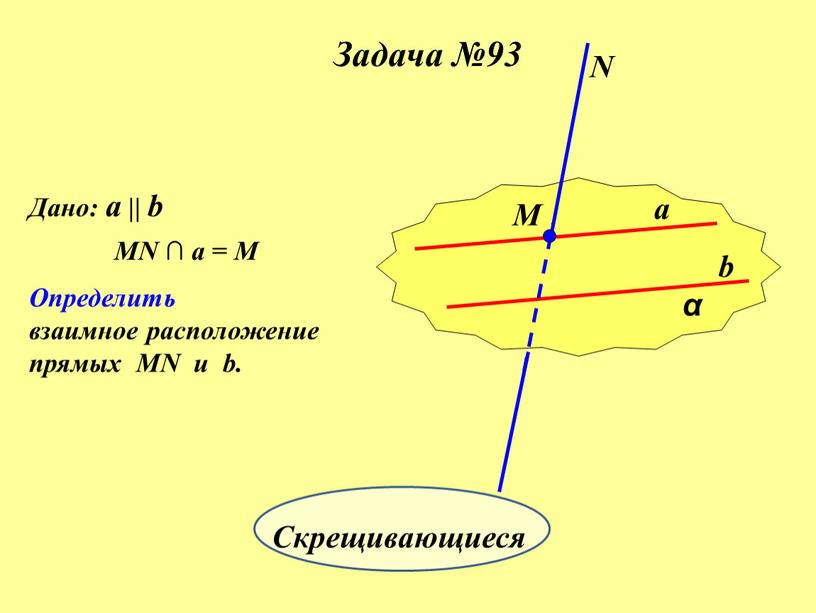
Задача №93 α a b М N Дано: a || b
Определить
взаимное расположение
прямых MN u b.
Видео:7 класс, 29 урок, Теоремы об углах, образованных двумя параллельными прямыми и секущейСкачать

Определить взаимное расположение прямых
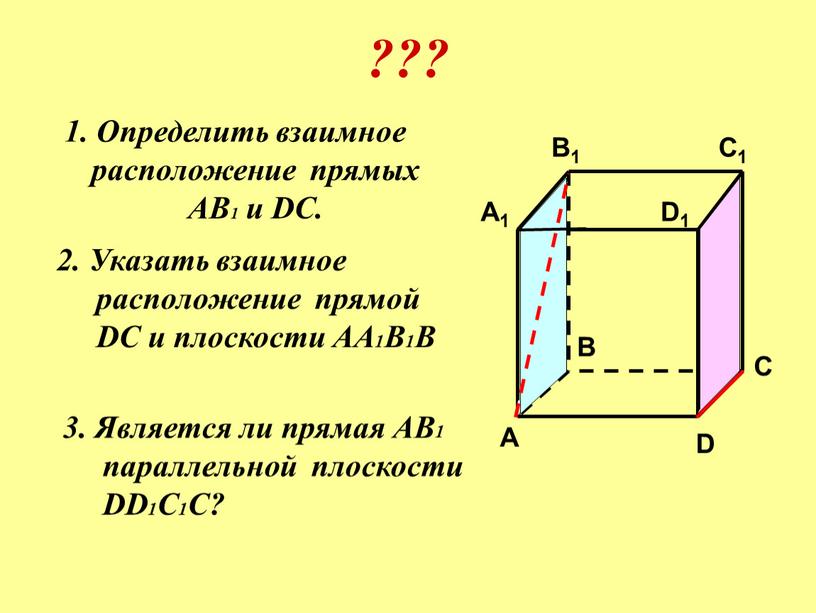
1. Определить взаимное
расположение прямых
АВ1 и DC.
2. Указать взаимное
расположение прямой
DC и плоскости АА1В1В
3. Является ли прямая АВ1
параллельной плоскости
DD1С1С?
Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

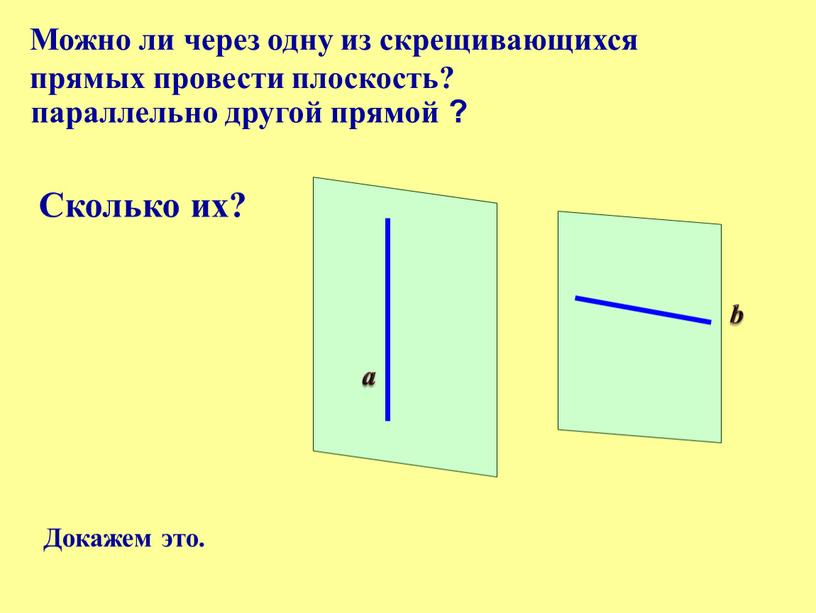
Можно ли через одну из скрещивающихся прямых провести плоскость?
Можно ли через одну из скрещивающихся
прямых провести плоскость?
параллельно другой прямой
Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

О существовании параллельных плоскостей, проходящих через скрещивающиеся прямые
О существовании параллельных плоскостей, проходящих через скрещивающиеся прямые
Видео:Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать

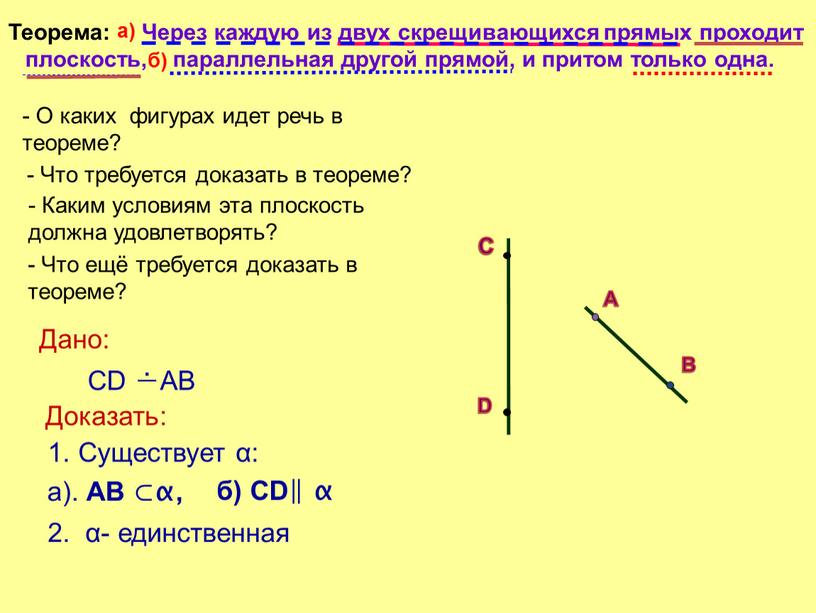
Теорема: Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна
Теорема: Через каждую из двух скрещивающихся прямых проходит
плоскость, параллельная другой прямой, и притом только одна.
— О каких фигурах идет речь в теореме?
— Что требуется доказать в теореме?
2. α- единственная
— Каким условиям эта плоскость должна удовлетворять?
а). AB ⊂α,
— Что ещё требуется доказать в теореме?
Видео:СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

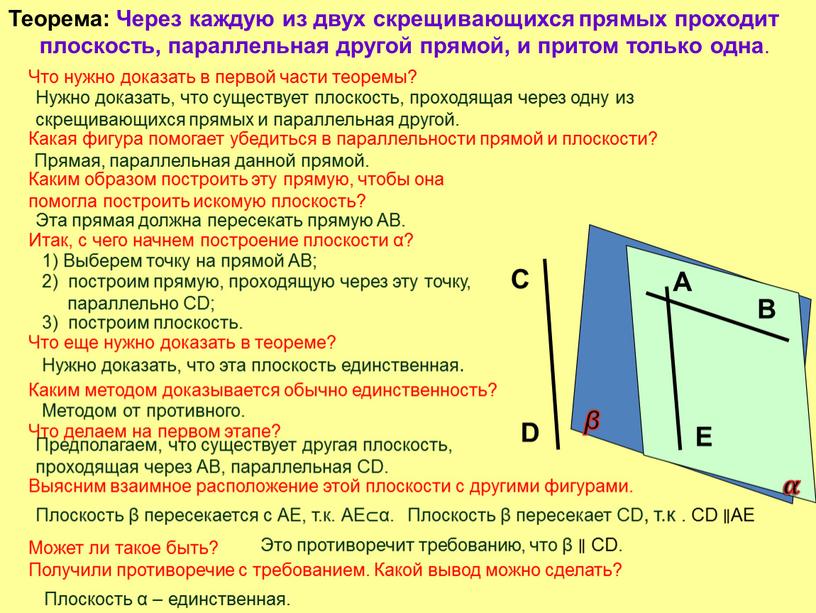
Теорема: Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна
Теорема: Через каждую из двух скрещивающихся прямых проходит
плоскость, параллельная другой прямой, и притом только одна.
Что нужно доказать в первой части теоремы?
Нужно доказать, что существует плоскость, проходящая через одну из
скрещивающихся прямых и параллельная другой.
Какая фигура помогает убедиться в параллельности прямой и плоскости?
Прямая, параллельная данной прямой.
Каким образом построить эту прямую, чтобы она
помогла построить искомую плоскость?
Эта прямая должна пересекать прямую АВ.
Итак, с чего начнем построение плоскости α?
Что еще нужно доказать в теореме?
2) построим прямую, проходящую через эту точку,
параллельно CD;
3) построим плоскость.
Нужно доказать, что эта плоскость единственная.
1) Выберем точку на прямой АВ;
Каким методом доказывается обычно единственность?
Методом от противного.
Что делаем на первом этапе?
Предполагаем, что существует другая плоскость,
проходящая через АВ, параллельная CD.
Выясним взаимное расположение этой плоскости с другими фигурами.
Плоскость β пересекается с АЕ, т.к. АЕ⊂α.
Получили противоречие с требованием. Какой вывод можно сделать?
Видео:Геометрия 10 класс (Урок№5 - Взаимное расположение прямых в пространстве.)Скачать

Презентация по геометрии 10 класс на тему
Видео:Геометрия 10 класс (Урок№6 - Параллельность плоскостей.)Скачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»
Сертификат и скидка на обучение каждому участнику
Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»
Свидетельство и скидка на обучение каждому участнику
Описание презентации по отдельным слайдам:
Постройте в заданной плоскости еще одну прямую b. Как она может располагаться относительно прямой а? Сколько таких случаев? пересекаются параллельны
Разбейте данные рисунки по группам, найдя какой–либо признак для разделения. 1 2 3 4 5 6
Проблема: новый способ расположения прямых.
Две прямые называются скрещивающимися, если они не лежат в одной плоскости. Определение М a b
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIi Наглядное представление о скрещивающихся прямых дают две дороги, одна из которых проходит по эстакаде, а другая под эстакадой.
Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся. Признак скрещивающихся прямых D В А C
а II b Три случая взаимного расположения двух прямых в пространстве М a b a b a b
Определить взаимное расположение прямых АВ1 и DC.
А D С В B1 С1 D1 А1 Каково взаимное положение прямых 1) AD1 и МN; 2) AD1 и ВС1; 3) МN и DC? N M
Задача. α a b М N Дано: a || b MN ∩ a = M Определить взаимное расположение прямых MN u b. Скрещивающиеся.
Через вершину А ромба АВСD проведена прямая а, параллельная диагонали ВD, а через вершину С – прямая b, не лежащая в плоскости ромба. Докажите, что: а) а и СD пересекаются; б) а и b скрещивающиеся прямые. В А C ? a D
А D С В B1 С1 D1 А1 Докажите, что прямые 1) AD и C1D1; 2) A1D и D1C; 3) AB1 и D1C скрещивающиеся. N M
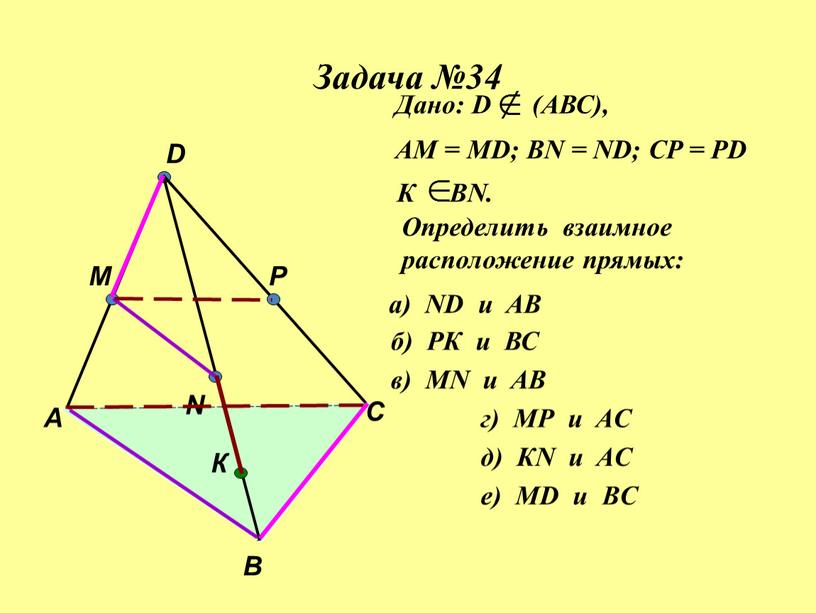
Задача А В С D M N P К Дано: D (АВС), АМ = МD; ВN = ND; CP = PD К ВN. Определить взаимное расположение прямых: б) МР и AС в) КN и AС г) МD и BС
Дано: точка А лежит вне плоскости DNK. Доказать: прямые AD и NK — скрещивающиеся А K N D Задача №1
Дано: b|| BC, прямая а не принадлежит плоскости АВС Доказать: прямые a и b — скрещивающиеся b а А С В D ГРУППА 2
ГРУППА 3 А В С m Указать взаимное расположение прямых m и СВ, если: Прямая m лежит в (АВС) и не имеет общих точек с АС. Прямая m не лежит в (АВС)
Группа 4 Дано: ABCD – квадрат КА не лежит в (АВС) Определить взаимное расположение прямых КА и CD А К В С D
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 968 человек из 79 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 338 человек из 71 региона
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 689 человек из 74 регионов
Ищем педагогов в команду «Инфоурок»
Дорогие коллеги представляю вам презентацию ,которая мне очень помогла в изучении скрещивающихся прямых 10 класс геометрия.
В данном материале вы найдете и повторение ,и изучение новой темы ,и закрепление.
Данный материал поможет даже слабым ученикам разобраться в данной теме.
Этот материал можно также использовать на последующих уроках,а также при закреплении и при подготовки обобщающего урока,а также можно при индивидуальном обучении использовать ученику, как подсказку при ответах на вопросы учителя.
Буду рада если вам также понравиться данный материал и будет использован при изучении данной темы.
- Миронова Елизавета ВалентиновнаНаписать 523 04.01.2015
Номер материала: ДБ-1340175
- 30.09.2020 0
- 30.09.2020 0
- 30.09.2020 0
- 30.09.2020 0
- 30.09.2020 0
- 30.09.2020 0
- 30.09.2020 0
- 30.09.2020 0
Не нашли то, что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В Госдуме предложили продлить каникулы для школьников до 16 января
Время чтения: 1 минута
В Минпросвещения рассказали о формате обучения школьников после праздников
Время чтения: 1 минута
Минпросвещения готовит рекомендации по построению «идеальной школы»
Время чтения: 1 минута
Глава СПЧ предложил ввести подготовительные курсы перед обучением в школе для детей мигрантов
Время чтения: 1 минута
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
ОНФ планирует решить проблему с низкими зарплатами водителей школьных автобусов в России
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.