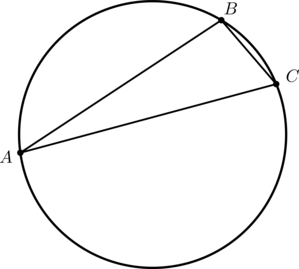
В выпуклом четырёхугольнике ABCD известны стороны и диагональ: AB = 3, BC = CD = 5, AD = 8, AC = 7.
а) Докажите, что вокруг этого четырёхугольника можно описать окружность.
Найдём косинусы углов ABC и ADC в треугольниках ABC и ADC соответственно:
поэтому ABC = 120°.
Далее,
поэтому ADC = 60°.
Тем самым сумма противоположных углов четырехугольника равна 180°, поэтому вокруг него можно описать окружность. Для вписанного четырёхугольника справедлива теорема Птолемея: произведение диагоналей четырёхугольника равно сумме произведений его противоположных сторон. Тогда то есть
откуда
Ответ: б)
Приведем решение пункта б) Тофига Алиева без использования теоремы Птолемея.
Заметим, что поскольку
Пусть
тогда в треугольнике BAD по теореме косинусов
В треугольнике BCD по теореме косинусов
Приравнивая выражения для BD 2 , получим
Приведем идею решения Юрия Зорина.
Углы BAC и BDC равны как вписанные углы, опирающиеся на дугу BC. По теореме косинусов найдём косинус угла BAC (он равен 11/14). Далее, зная, что косинусы равных углов равны, из треугольника BDC найдем по теореме косинусов искомый отрезок BD.
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а) при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, Содержание Видео:#58. Олимпиадная задача о четырехугольникеСкачать  Илья решает задачу по геометрии в которой дан четырехугольник авсд причем ав 5Артикул: 1135422Название:Илья решает задачу по геометрии, в которой дан четырёхугольник ABCD, причём AB=5, BC=6, CD=4, AD=10. В условии задачи сказано, что одна из вершин является центром некоторой окружности и Илья думает, какую вершину ему выбрать в качестве центра этой самой окружности. Известно, что вероятность выбора каждой конкретной вершины пропорциональна сумме длин сторон четырёхугольника ABCD, проходящих через эту вершину. Какова вероятность того, что Илья выберет вершину B? Процесс покупки очень прост и состоит всего из пары действий: Видео:Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать  Тренировочные варианты «Школково». Тренировочный вариант №4Вика хочет купить билет в кино для себя и подруги. Один билет стоит (500) рублей, но при покупке сразу двух билетов предоставляется скидка (3%) на оба билета. У Вики в кармане (1200) рублей. Все оставшиеся после покупки билетов деньги она хочет потратить на попкорн, одна пачка которого стоит (30) рублей. Сколько пачек попкорна сможет купить Вика? На билеты Вика потратит с учётом скидки (2cdot 500cdot (1 — 0,03) = 970) рублей. Тогда на попкорн у неё остаётся (1200 — 970 = 230) рублей. Количество пачек попкорна, которое сможет купить Вика, равно округлённому в меньшую сторону частному чисел (230) и (30) , то есть Вика сможет купить (7) пачек попкорна. На плоскости (Oxv) показана взаимосвязь скорости (v) материальной точки и её положения (x) . Определите наибольшую скорость, с которой точка может пройти положение (x = 2) . Для ответа на поставленный вопрос надо найти на данной кривой точку, у которой (x = 2) . Таких точек две: (P(2; 2)) и (Q(2; 4)) . При этом скорость больше в точке (Q) (и равна она (4) ). В треугольнике (ABC) точка (M) лежит на стороне (AC) (но не совпадает с точкой (A) или точкой (C) ), причём (CM = MB) . Кроме того, (CB = MB) . Найдите сумму меньшего и большего углов треугольника (ABC) . Ответ дайте в градусах. Так как (CM = MB = BC) , то треугольник (MBC) – равносторонний, тогда (angle MCB = 60^circ) . Так как сумма углов треугольника равна (180^circ) , то угол, равный (60^circ) , не может быть большим и не может быть меньшим углом треугольника. Треугольник (ABC) не равносторонний (так как (A) не совпадает с (M) ), причём (angle ACB = 60^circ) , тогда один из углов (A) и (B) больше (60^circ) , а другой меньше (60^circ) . Таким образом, [angle A + angle B = 180^circ — 60^circ = 120^circ] – искомая сумма углов. Илья решает задачу по геометрии, в которой дан четырёхугольник (ABCD) , причём (AB = 5) , (BC = 6) , (CD = 4) , (AD = 10) . В условии задачи сказано, что одна из вершин является центром некоторой окружности и Илья думает, какую вершину ему выбрать в качестве центра этой самой окружности. Известно, что вероятность выбора каждой конкретной вершины пропорциональна сумме длин сторон четырёхугольника (ABCD) , проходящих через эту вершину. Какова вероятность того, что Илья выберет вершину (B) ? Через вершину (A) проходят стороны (AB) и (AD) , их сумма: (AB + AD = 15) . Через вершину (B) проходят стороны (AB) и (BC) , их сумма: (AB + BC = 11) . Через вершину (C) проходят стороны (BC) и (CD) , их сумма: (BC + CD = 10) . Через вершину (D) проходят стороны (CD) и (DA) , их сумма: (CD + DA = 14) . Обозначим вероятность выбора вершины (A) через (P(A)) (для остальных вершин аналогично). Тогда по условию имеем: [P(A) = 15k,qquad P(B) = 11k,qquad P(C) = 10k,qquad P(D) = 14k,,] но (P(A) + P(B) + P(C) + P(D) = 1) , тогда (k = 0,02) , откуда находим: (P(B) = 0,22) . Данное уравнение можно переписать в виде [3^ + 3cdot 3^ = 4] Пусть (t = 3^) , (t > 0) , тогда [t^2 + 3t — 4 = 0,,] откуда (t_1 = 1) , (t_2 = -4) , но (t > 0) , следовательно, подходит только (t = 1) . Тогда (3^ = 1 = 3^0) , что равносильно (x + 1 = 0) , то есть (x = -1) . Радиус окружности, описанной около треугольника (ABC) , равен (R) . Большая сторона треугольника (ABC) равна (10) , а (angle ABC = 150^circ) . Найдите (R) . В треугольнике против большего угла лежит большая сторона, тогда (AC = 10) . По теореме синусов [2R = dfrac = dfrac = 20,,] откуда (R = 10) . Найдите ординату точки касания графика функции (y = sin^2 x) и прямой (y = x + 0,5 — dfrac) . Если указанные графики касаются в точке ((x_0; y_0)) , то производные соответствующих функций равны в точке (x_0) : [2sin x_0cdot cos x_0 = 1qquadLeftrightarrowqquad sin 2x_0 = 1qquadLeftrightarrowqquad x_0 = dfrac + pi k, kinmathbb] При этом необходимо, чтобы при (x = x_0) значения соответствующих функций совпадали: [sin^2 x_0 = x_0 + 0,5 — dfrac,,] но при (x_0 = dfrac + pi k, kinmathbb) имеем: (sin^2 x_0 = 0,5) , тогда [0,5 = x_0 + 0,5 — dfrac,,] куда подходит только (x_0 = dfrac) . Таким образом, для касания указанных графиков в точке ((x_0; y_0)) необходимо, чтобы было выполнено (x_0 = dfrac) . Но этого и достаточно, ведь при (x_0 = dfrac) совпадают значения функций и их производных. В итоге, [y_0 = sin^2 x_0 = 0,5] Про прямые круговые цилиндры (C_1) и (C_2) известно, что у (C_1) радиус основания в два раза больше, чем у (C_2) , но у (C_2) высота в три раза больше, чем у (C_1) . Найдите отношение объёма цилиндра (C_2) к объёму (C_1) . Обозначим высоту цилиндра (C_1) через (h_1) , а высоту цилиндра (C_2) через (h_2) . Обозначим радиус основания цилиндра (C_1) через (r_1) , а радиус основания цилиндра (C_2) через (r_2) . Тогда [r_1 = 2r_2,qquad h_2 = 3h_1,.] Объём цилиндра (C_1) равен (pi ^2 h_1 = 4pi ^2 h_1) , а объём цилиндра (C_2) равен (3pi ^2 h_1) , тогда [dfrac<V_><V_> = dfrac<3pi ^2 h_1><4pi ^2 h_1> = 0,75] Найдите значение выражения [dfrac + dfrac] при (a = sqrt[3]) , (b = 2) . Подставим (b = 2) в исходное выражение, учитывая, что (a > 0) : [dfrac + dfrac = dfrac + 1 = 1,5] Рейтинг студентов некоторого университета вычисляется на основании показателей (m) , (n) , (k) по следующей формуле: [dfrac,.] Рейтинг Димы равен (10) , а Тимур имеет следующие значения показателей: (m = 10) , (k = 3) . Какое минимальное значение показателя (n) может иметь Тимур, чтобы его рейтинг был не меньше, чем рейтинг Димы, если (n geqslant 0) ? Подставим известные значения для вычисления рейтинга Тимура: [dfrac] Полученная величина должна быть не меньше (10) , причём (ngeqslant 0) , следовательно, (n + 3 > 0) , тогда [dfracgeqslant 10qquadLeftrightarrowqquad n^2 + 5n + 70 geqslant 0qquadLeftrightarrowqquad (n + 2,5)^2 + 63,75 geqslant 0,,] что выполнено при всех (n) . Таким образом, наименьшее допустимое значение (n) равно (0) . Илья решил в течение некоторого периода каждый день отжиматься в два раза больше, чем в предыдущий день. В четвёртый и последний день вместе он отжался в десять раз больше, чем в третий день. Сколько раз суммарно отжался Илья за этот период, если в первый день он отжался три раза? В третий день Илья сделал (3cdot 2^ = 12) отжиманий, а в четвёртый день он сделал (3cdot 2^ = 24) отжимания. Так как в четвёртый и последний день вместе он отжался в десять раз больше, чем в третий день, то в четвёртый и последний день он отжался (12cdot 10 = 120) раз, следовательно, в последний день он отжался (120 — 24 = 96) раз. Пусть (n) дней длился период отжиманий Ильи, тогда [3cdot 2^ = 96qquadLeftrightarrowqquad 2^ = 32qquadLeftrightarrowqquad n = 6,.] Суммарное количество отжиманий, сделанное Ильёй, равно [3cdotdfrac = 189,.] Найдите наименьшее значение функции (y = 3x^3e^ + 2x^2e^ + xe^) на отрезке ([0; 2]) . (y’ = 9x^2e^ + 9x^3e^ + 4xe^ + 4x^2e^ + e^x + xe^x) Так как при любом (xin[0; 2]) верно: (e^x > 0) , (e^ > 0) , (e^ > 0) , (x geqslant 0) , (x^2geqslant 0) , (x^3geqslant 0) , то на ([0; 2]) (y’ > 0) , следовательно на отрезке ([0; 2]) функция (y) возрастает, тогда наименьшее значение она достигает при (x = 0) : [y(0) = 0,.] При любом (a > 0) функция (x^a) возрастает на ([0; 2]) ; 2) при любом (b > 0) функция (e^) возрастает на ([0; 2]) ; 3) произведение возрастающих функций снова возрастающая функция; 4) сумма возрастающих функций снова возрастающая функция. Из этих четырёх фактов следует, что данная в условии функция возрастает на ([0; 2]) , следовательно, наименьшее на ([0; 2]) значение она принимает в левом конце этого отрезка, то есть её наименьшее значение равно (y(0) = 0) . Заметим, что функция является сложной относительно (t(x)=xcdot e^x) : (y(t(x))=3t^3+2t^2+t) . Следовательно, ее производную можно искать как производную сложной функции: [y’=(3t^3+2t^2+t)’_cdot t’_x=(9t^2+4t+1)_cdot (xcdot e^x+e^x)= (9t^2+4t+1)_cdot e^x(x+1)] Заметим, что производная равна нулю тогда и только тогда, когда либо (x+1=0) , либо ((9t^2+4t+1)_=0) (т.к. (e^x>0) при всех (x) ). Второе уравнение не имеет решений, т.к. дискриминант (D . Следовательно, имеем [x+1=0quadLeftrightarrowquad x=-1.] Найдем знаки производной на отрезке ([0;2]) : Следовательно, на отрезке ([0;2]) функция (y(x)) возрастает, значит, наименьшее значение она принимает в начале отрезке. Тогда [y_<text>(x)=y(0)=0.] 📽️ ВидеоЗадача первоклассника в 1 шаг! Невероятное решение!Скачать  №951. Докажите, что четырехугольник ABCD является прямоугольником, и найдите егоСкачать  №371. Докажите, что выпуклый четырехугольник ABCD является параллелограммом,Скачать  Задача, которую боятсяСкачать  Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать  8 класс, 3 урок, ЧетырехугольникСкачать  Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать  Четырёхугольник и его элементы – 8 класс геометрияСкачать  №370. Найдите углы выпуклого четырехугольника, если они пропорциональны числам 1, 2, 4, 5.Скачать  ЧЕТЫРЕХУГОЛЬНИК 8 класс РЕШЕНИЕ ЗАДАЧ АтанасянСкачать  Миникурс по геометрии. ЧетырехугольникиСкачать  16) Четырехугольник АВСD описан около окружности, AD=7, DC=12, BC=13. Найдите AB. Математика огэ.Скачать  3 правила для вписанного четырехугольника #shortsСкачать  8 класс, 6 урок, ТрапецияСкачать  Трапеция, решение задач. Вебинар | МатематикаСкачать  Математика| Геометрия 8 класса в одной задачеСкачать  Геометрия. Вся теория по четырехугольникам. Задача №12Скачать  Просто красота! САМ В ШОКЕ!Скачать  |