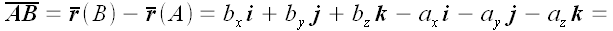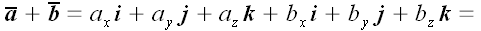И жи к вектора

В. Г. Автор. Векторная и тензорная алгебра для будущих физиков и техников

.Геометрическое определение вектора

.Алгебраические операции над направленными отрезками

..Сложение направленных отрезков

..Умножение направленных отрезков на число

..Параллельное проектирование вектора в пространстве

. Проекция точки на плоскость

. Проекция вектора на плоскость

..Ортогональная проекция вектора в пространстве

. Ортогональная проекция вектора на плоскость

. Ортогональная проекция вектора на прямую и направленную ось

..Векторы в трехмерном геометрическом пространстве

..Линейная зависимость векторов и размерность пространства

.Декартова система координат

..Различные формы записи векторов

..Линейные операции над векторами в координатной форме

. Свойства скалярного умножения

. Скалярное умножение в декартовых координатах

..Некоторые примеры использования скалярного умножения

..Площадь параллелограмма, построенного на векторах

..Задачи на применение определителей

..Определитель третьего порядка и его свойства

..Векторное умножение векторов базиса декартовой системы координат

.Ковариантные и контравариантные координаты вектора

..Индексная форма записи для выражений с определителями

..Свойства символов Веблена

..Операция векторного умножения в произвольных косоугольных координатах

.Линейный оператор и его матрица

.Доказательство теоремы об определителе

.Общие определения алгебраических операций с тензорами

.Примеры на применение тензоров в физике

..Задачи на тождественные преобразования

Базис, состоящий из произвольной тройки некомпланарных векторов, принято называть произвольной косоугольной системой координат. Такая система неудобна для практических вычислений и не очень естественна. На практике никто не измеряет длину в метрах, ширину в дюймах, а высоту в лаптях. Если мы и пользуемся произвольной косоугольной системой координат, то эта мера вынужденная. Например, даже если мы свяжем с упругим телом какую-либо удобную для нас систему координат, то в процессе деформации упругого тела эта система, мягко говоря, покоробится. Есть проблемы, при изучении которых, мы принципиально не можем воспользоваться какой-либо специальной системой координат.

В тех случаях, когда обстоятельства позволяют, и задача этого требует, удобнее использовать некую специальную систему координат. Таких систем изобретено достаточно много: цилиндрическая, сферическая, полярная, эллиптическая и т.д. Очень часто оказывается удобна так называемая декартовая система координат.

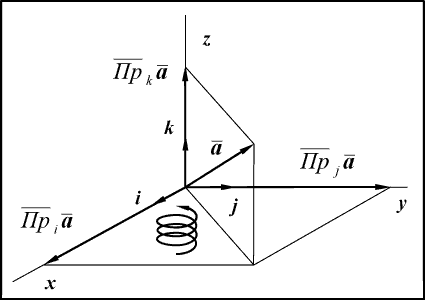
Декартовой называется система, базисные векторы которой взаимно ортогональны, по модулю равны единице и образуют правую тройку. Обозначаются базисные векторы латинскими буквами, которые называются, в соответствии с традицией, по-французски: i – и, j – жи, k – ка (рис. 14).

Рис. 14

Правил, позволяющих отличить правую тройку векторов от левой, имеется несколько. Из них наиболее часто используются четыре:

1. Правило левой руки.

Если кисть левой руки направить по направлению первого вектора и расположить ее так, чтобы второй вектор был направлен в ладонь, и если при этом большой палец левой руки будет направлен так же как третий вектор, то векторы образуют правую тройку векторов.

2. Правило правого винта.

Если первый вектор поворачивать по кратчайшему расстоянию в сторону второго, то третий вектор правой тройки векторов должен быть направлен в ту же сторону, в которую при таком вращении будет заворачиваться правый винт. Это правило на рис. 14 проиллюстрировано изображением спирали.

Остальные два правила не имеют названия.

3. Три вектора образуют правую тройку векторов, если при наблюдении из конца третьего вектора вращение первого по кратчайшему расстоянию в сторону второго происходит против часовой стрелки.

4. Если мы находимся внутри трехгранного угла, образованного тройкой векторов, и если при этом поворот от первого вектора ко второму, а затем к третьему должны выполнить против часовой стрелки, то векторы образуют правую тройку векторов.

Можно предложить и еще одно правило:

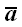
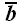
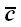
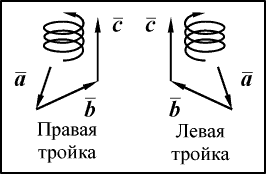
5. Векторы , и в указанном порядке образуют правую тройку векторов, если, будучи выстроенными в том же порядке друг за другом, они образуют правую спираль (рис. 15).

Рис. 15

Наличие большого количества правил говорит о том, что все они не очень удобны, и для того, чтобы научиться отличать правую тройку векторов от левой, требуется определенная тренировка.

Вектор i (и) обычно совмещают с осью x , вектор j (жи) – с осью y , а вектор k (ка) – с осью z .

Поскольку базисные векторы декартовой системы координат взаимно ортогональны, то координаты произвольного вектора в такой системе совпадают с его ортогональными проекциями.

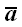
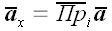
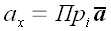
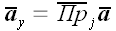
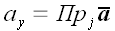
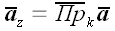
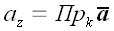
Пример обозначения координат произвольного вектора (рис. 14).

, ;

, ;

, .

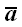
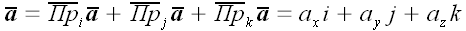
Следовательно, в декартовой системе координат произвольный вектор может быть представлен в виде:

.

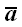
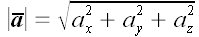
Модуль вектора , как видно из рис. 14, вычисляется как корень квадратный из суммы квадратов его координат: .

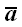
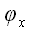
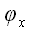
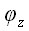
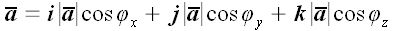
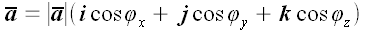
Если обозначить углы между вектором и векторами i , j и k соответственно , и , то разложение вектора по векторам базиса запишется так: или .

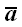
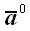
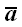
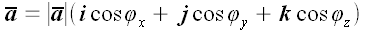
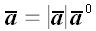
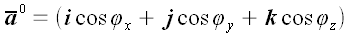
Вектор, совпадающий по направлению с вектором и имеющий единичную длину, называется направляющим вектором, или ортом-вектором, или просто ортом. Орт-вектор обозначается обычно с ноликом в правом верхнем углу: – орт-вектор вектора .

и , то

.

Косинусы в последнем выражении, которые являются координатами орта-вектора, называются направляющими косинусами.

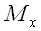
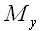
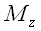
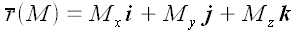
Вектор, проведенный из начала координат в некоторую точку M , называется радиусом-вектором этой точки. Координаты точки (, и ) и координаты ее радиуса-вектора совпадают: .

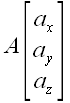
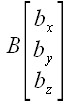
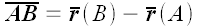
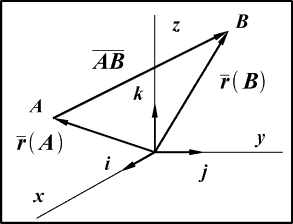
Если нам заданы в пространстве две точки и , то координаты вектора можно вычислить, воспользовавшись тем, что

(рис. 16).

Рис. 16

Выразив координаты радиусов-векторов через координаты точек, мы получим:

.

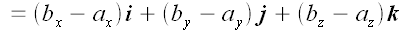
Следовательно, координаты вектора, проведенного из точки в A точку B , равны разности соответствующих координат этих точек.

.. Различные формы записи векторов

Принято различать координатную и векторную формы записи векторов. До сих пор мы пользовались только векторной формой записи. Но если мы выберем и зафиксируем в пространстве некоторую систему координат, то для задания любого вектора нам будет достаточно задать его координаты. Координаты, то есть три числа, взятые в определенном порядке, однозначно определяют вектор в выбранной системе координат. Поэтому можно записать: 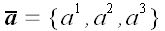. Слева в этом равенстве стоит вектор, следовательно, под таблицей чисел, стоящей справа, необходимо понимать вектор с соответствующими координатами. Такая форма записи часто используется в векторной алгебре и называется координатной.

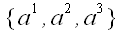
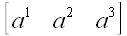
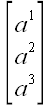
Таблицу можно записать по-разному, например так, как это принято в матричной алгебре: или .

Если под этими таблицами также понимать вектор с соответствующими координатами, то все эти таблицы представляют один и тот же вектор. Значит, мы имеем право записать:

.

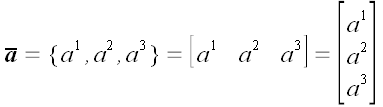
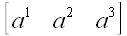
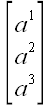
Если рассматривать это равенство, как векторное, то его следует признать правильным. Однако, с точки зрения матричной алгебры, таблицы и представляют собой различные матрицы, и между ними не может быть поставлен знак равенства. Можно было бы проигнорировать эту проблему, поскольку матричная алгебра является самостоятельной наукой и, если не смешивать матричную и векторную алгебры, то недоразумений не возникает. Кроме того, никто не заставляет использовать матричный формат записи координат векторов. Общепринятой является форма записи координат векторов в фигурных скобках, которая не используется в теории матриц. Выходит, что, если ограничиться только общепринятой формой, то проблем не возникает. Но дело все в том, что матричная и векторная алгебры близки и по духу, и по решаемым проблемам. Когда дело доходит до реальных вычислений с векторами, полезно использовать матричные методы и обозначения. Короче говоря, матричную и векторную алгебры полезно максимально интегрировать. Для того, чтобы при этом возникало меньше проблем, мы слегка модернизируем обозначения:

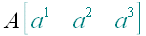
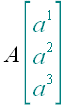
1. Обозначение точек , или .

Точки будем обозначать большими буквами латинского алфавита. То, что обведено зеленоватым цветом, является необязательной частью обозначения. К необязательной части обозначения относится матрица с координатами точки.

Примеры: A , , .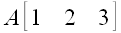

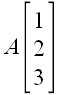
2. Обозначение векторов

, , , .

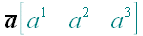
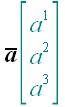
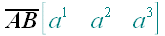
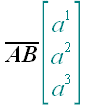
Примеры: , , .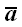

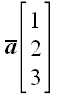
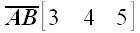
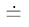
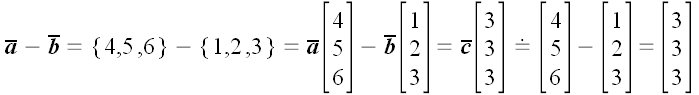
Кроме того, чтобы легче было переходить от векторов к матрицам и наоборот, введем знак «соответствия» «» – знак «равно» с точкой наверху. Этим знаком мы будем объединять одинаковые по смыслу векторные и матричные выражения, например,

.

Прочитать это выражение можно так: «Разнице векторов слева соответствует разность матриц справа».

Мы не будем давать точного определения для введенного нами знака «соответствия», рассматривая его в качестве «осторожного» знака равенства. Он должен напоминать, что хотя выражения, объединенные им, в известной степени, равны по смыслу, следует соблюдать осторожность при формальных преобразованиях.

..Линейные операции над векторами в координатной форме

Линейные операции над векторами можно выполнять как в векторной, так и в координатной формах, например:

1. Сложение векторов.

.

.

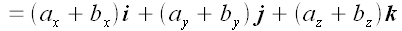
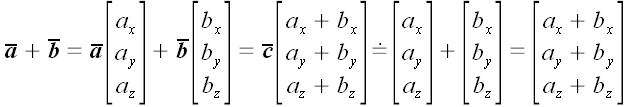
2. Умножение вектора на число.

.

.

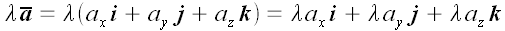
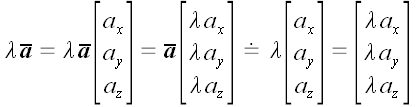
Видео:Вектор А - Жизнь (Official video)Скачать

Знакомимся с вектором

Основы линейной алгебры для тех, кого это миновало в универе.

Вы наверняка слышали много историй о программистах, которые учились в технических вузах, изучали высшую математику и теперь пользуются этими знаниями в программировании. И если кого-то это не коснулось, может быть ощущение, что он пропустил в жизни что-то важное.

Будем это исправлять. Попробуем разобрать некоторые базовые понятия из математики за пределами школьной программы. И заодно покажем, как оно связано с программированием и для каких задач полезно.

⚠️ Математики, помогайте. Мы тут многое упростили, поэтому будем рады увидеть ваши уточнения и замечания в комментариях.

Видео:Зачем нужен ВЕКТОР. Объяснение смыслаСкачать

Линейная алгебра

Есть математика: она изучает абстрактные объекты и их взаимосвязи. Благодаря математике мы знаем, что если сложить два объекта с ещё двумя такими же объектами, то получится четыре объекта. И неважно, что это были за объекты: яблоки, козы или ракеты. Математика берёт наш вещественный мир и изучает его более абстрактные свойства.

Внутри математики есть алгебра: если совсем примитивно, то в алгебре мы вместо чисел начинаем подставлять буквы и изучать ещё более абстрактные свойства объектов.

Например, мы знаем, что если a + b = c , то a = c − b . Мы не знаем, что стоит на местах a, b или c, но для нас это такой абстрактный закон, который подтверждается практикой.

Внутри алгебры есть линейная алгебра — она изучает векторы, векторные пространства и другие абстрактные понятия, которые в целом относятся к некой упорядоченной информации. Например, координаты ракеты в космосе, биржевые котировки, расположение пикселей в изображении — всё это примеры упорядоченной информации, которую можно описывать векторами. И вот их изучает линейная алгебра.

В программировании линейная алгебра нужна в дата-сайенс, где из упорядоченной информации создаются алгоритмы машинного обучения.

Если представить линейную алгебру в виде дома, то вектор — это кирпич, из которого всё состоит. Сегодня разберёмся, что такое вектор и как его понимать.

Видео:Вектор А — В порядке (Official video)Скачать

Что такое вектор

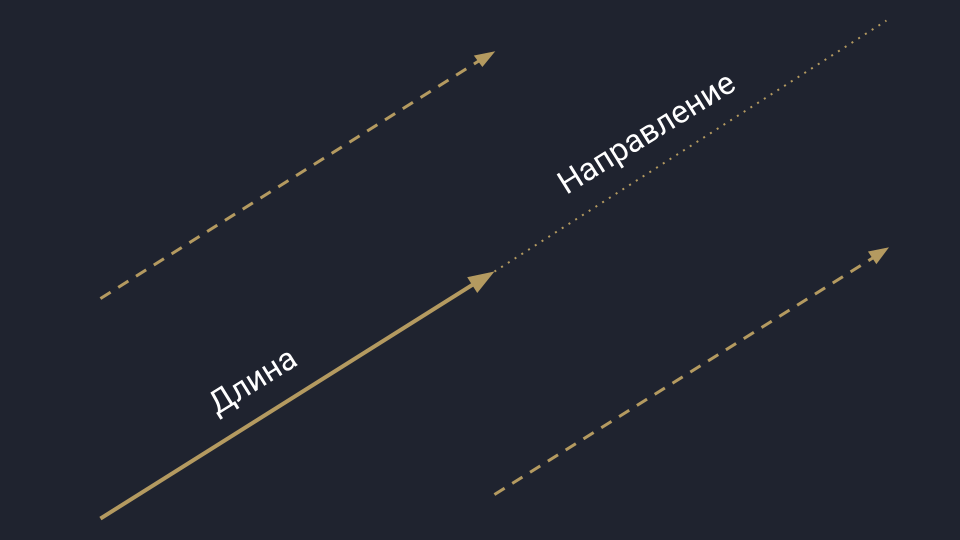
Вы наверняка помните вектор из школьной программы — это такая стрелочка. Она направлена в пространство и измеряется двумя параметрами: длиной и направлением. Пока длина и направление не меняются, вектор может перемещаться в пространстве.

Физическое представление вектора: есть длина, направление и нет начальной точки отсчёта. Такой вектор можно как угодно двигать в пространстве

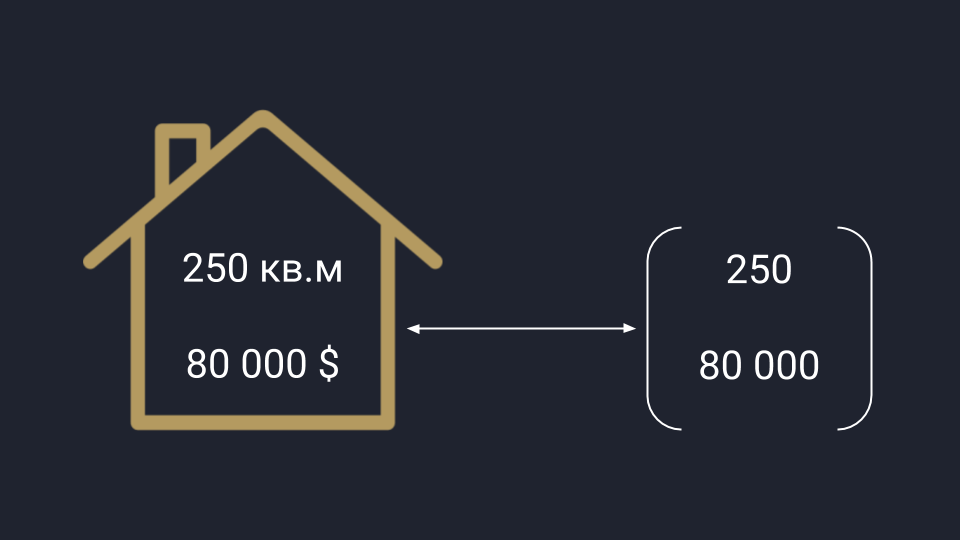
У аналитиков вектор представляется в виде упорядоченного списка чисел: это может быть любая информация, которую можно измерить и последовательно записать. Для примера возьмём рынок недвижимости, который нужно проанализировать по площади и цене домов — получаем вектор, где первая цифра отвечает за площадь, а вторая — за цену. Аналогично можно сортировать любые данные.

Аналитическое представление вектора: данные можно перевести в числа

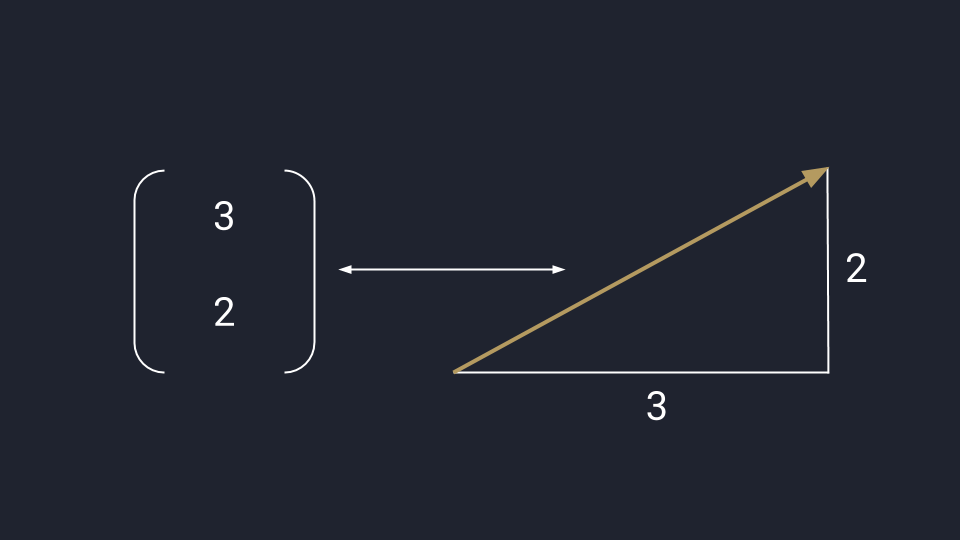
Математики обобщают оба подхода и считают вектор одновременно стрелкой и числом — это связанные понятия, перетекающие друг в друга в зависимости от задачи. В одних случаях удобней считать, а в других — показать всё графически. В обоих случаях перед нами вектор.

Математическое представление вектора: данные можно перевести в числа или график

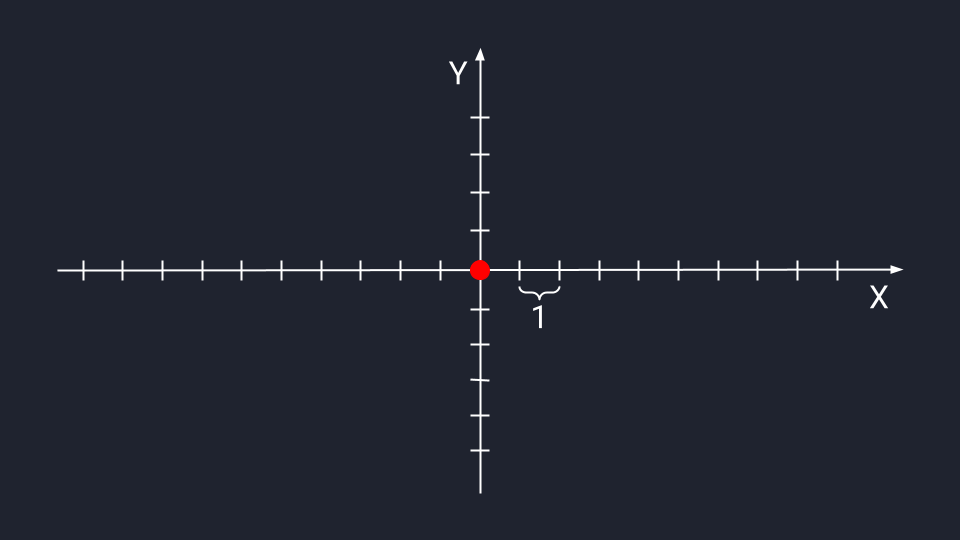
В дата-сайенс используется математическое представление вектора — программист может обработать данные и визуализировать результат. В отличие от физического представления, стрелки векторов в математике привязаны к системе координат Х и У — они не блуждают в пространстве, а исходят из нулевой точки.

Векторная система координат с базовыми осями Х и Y. Место их пересечения — начало координат и корень любого вектора. Засечки на осях — это отрезки одной длины, которые мы будем использовать для определения векторных координат

👉 Получается, вектор – это такой способ записывать, хранить и обрабатывать не одно число, а какое-то организованное множество чисел. Благодаря векторам мы можем представить это множество как единый объект и изучать его взаимодействие с другими объектами.

Например, можно взять много векторов с ценами на недвижимость, как-то их проанализировать, усреднить и обучить на них алгоритм. Без векторов это были бы просто «рассыпанные» данные, а с векторами — порядок.

Видео:Вектор А - ЛирикаСкачать

Как записывать

Вектор можно записать в строку или в столбец. Для строчной записи вектор обозначают одной буквой, ставят над ней черту, открывают круглые скобки и через запятую записывают координаты вектора. Для записи в столбец координаты вектора нужно взять в круглые или квадратные скобки — допустим любой вариант.

Строгий порядок записи делает так, что каждый набор чисел создаёт только один вектор, а каждый вектор ассоциируется только с одним набором чисел. Это значит, что если у нас есть координаты вектора, то мы их не сможем перепутать.

Способы записи вектора

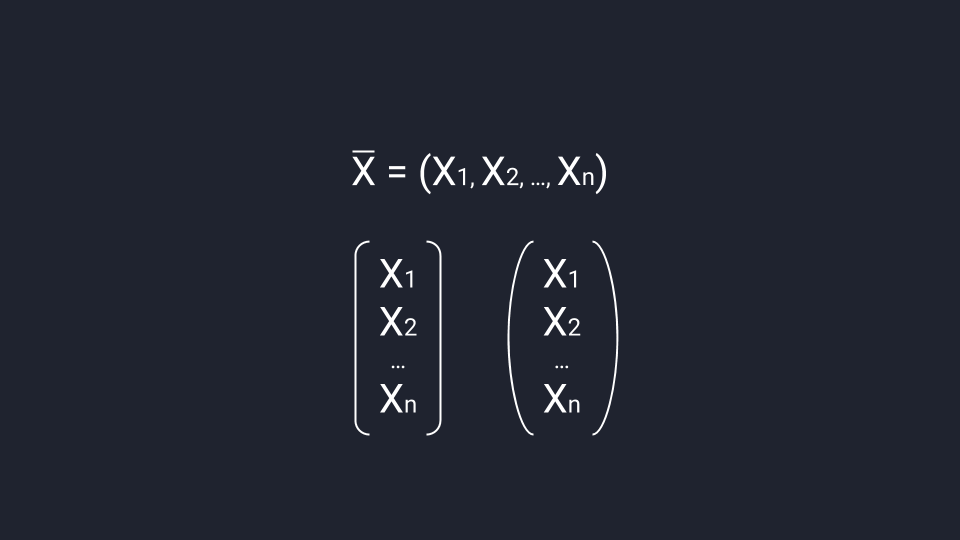
Скаляр

Помимо понятия вектора есть понятие скаляра. Скаляр — это просто одно число. Можно сказать, что скаляр — это вектор, который состоит из одной координаты.

Помните физику? Есть скалярные величины и есть векторные. Скалярные как бы описывают просто состояние, например, температуру. Векторные величины ещё и описывают направление.

Видео:До концаСкачать

Как изображать

Вектор из одного числа (скаляр) отображается в виде точки на числовой прямой.

Графическое представление скаляра. Записывается в круглых скобках

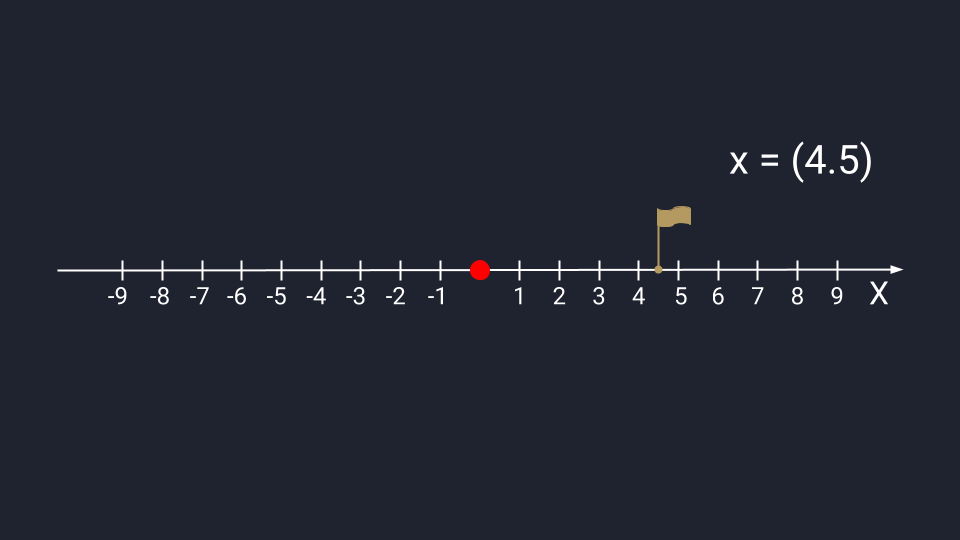
Вектор из двух чисел отображается в виде точки на плоскости осей Х и Y. Числа задают координаты вектора в пространстве — это такая инструкция, по которой нужно перемещаться от хвоста к стрелке вектора. Первое число показывает расстояние, которое нужно пройти вдоль оси Х; второе — расстояние по оси Y. Положительные числа на оси Х обозначают движение вправо; отрицательные — влево. Положительные числа на оси Y — идём вверх; отрицательные — вниз.

Представим вектор с числами −5 и 4. Для поиска нужной точки нам необходимо пройти влево пять шагов по оси Х, а затем подняться на четыре этажа по оси Y.

Графическое представление числового вектора в двух измерениях

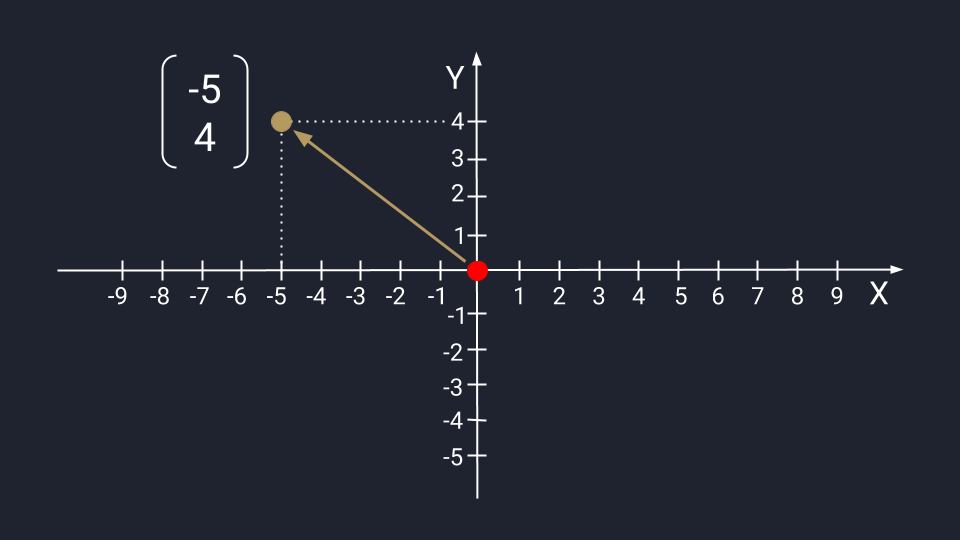
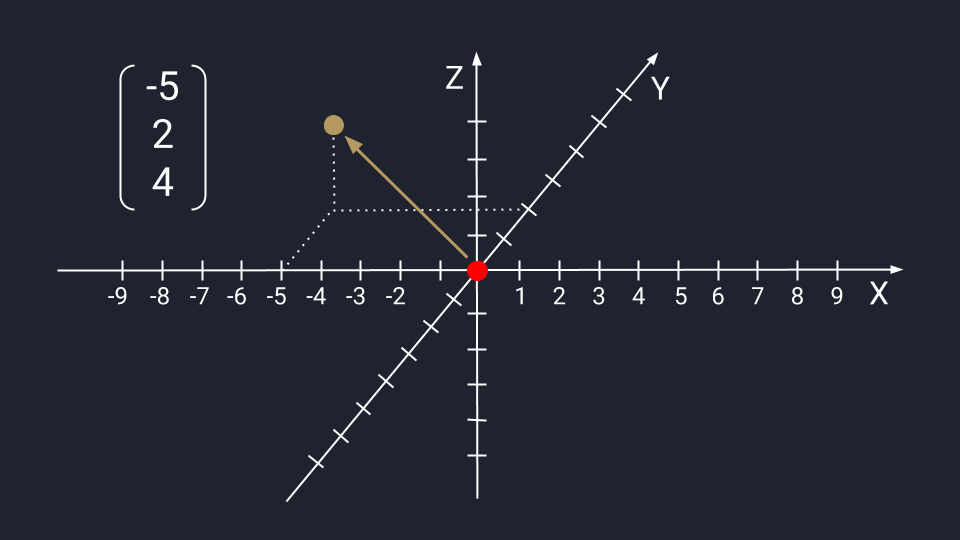
Вектор из трёх чисел отображается в виде точки на плоскости осей Х, Y и Z. Ось Z проводится перпендикулярно осям Х и У — это трёхмерное измерение, где вектор с упорядоченным триплетом чисел: первые два числа указывают на движение по осям Х и У, третье — куда нужно двигаться вдоль оси Z. Каждый триплет создаёт уникальный вектор в пространстве, а у каждого вектора есть только один триплет.

Если вектор состоит из четырёх и более чисел, то в теории он строится по похожему принципу: вы берёте координаты, строите N-мерное пространство и находите нужную точку. Это сложно представить и для обучения не понадобится.

Графическое представление числового вектора в трёх измерениях. Для примера мы взяли координаты −5, 2, 4

Помните, что все эти записи и изображения с точки зрения алгебры не имеют отношения к нашему реальному трёхмерному пространству. Вектор — это просто какое-то количество абстрактных чисел, собранных в строгом порядке. Вектору неважно, сколько там чисел и как их изображают люди. Мы же их изображаем просто для наглядности и удобства.

Например, в векторе спокойно может быть 99 координат. Для его изображения нам понадобилось бы 99 измерений, что очень проблематично на бумаге. Но с точки зрения вектора это не проблема: перемножать и складывать векторы из двух координат можно так же, как и векторы из 9999999 координат, принципы те же.

Видео:Вектор А - До концаСкачать

И зачем нам это всё

Вектор — это «кирпичик», из которого строится дата-сайенс и машинное обучение. Например:

• На основании векторов получаются матрицы. Если вектор — это как бы линия, то матрица — это как бы плоскость или таблица.
• Машинное обучение в своей основе — это перемножение матриц. У тебя есть матрица с данными, которые машина знает сейчас; и тебе нужно эту матрицу «дообучить». Ты умножаешь существующую матрицу на какую-то другую матрицу и получаешь новую матрицу. Делаешь так много раз по определённым законам, и у тебя обученная модель, которую на бытовом языке называют искусственным интеллектом.

Кроме того, векторы используются в компьютерной графике, работе со звуком, инженерном и просто любом вычислительном софте.

И давайте помнить, что вектор — это не какая-то сложная абстрактная штука, а просто сумка, в которой лежат числа в определённом порядке. То, что мы называем это вектором, — просто нюанс терминологии.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Что дальше

В следующий раз разберём операции с векторами. Пока мы готовим материал — рекомендуем почитать интервью с Анастасией Никулиной. Анастасия ведёт ютуб-канал по дата-сайнс и работает сеньором дата-сайентистом в Росбанке.

Видео:Вектор А - Напоследок (Official mood video)Скачать

Вектор: определение и основные понятия

Видео:Вектор А - Жизнь (слив полного трэка + текст) #ВекторА #Вектор #АндеграундСкачать

Определение вектора

рис. 1

Видео:Скалярное произведение векторов. 9 класс.Скачать

Обозначение вектора

Вектор началом которого есть точка А, а концом — точка В, обозначается AB (рис.1). Также вектора обозначают одной маленькой буквой, например a .

Видео:Как побороть страх? #сомнения #страх #интервьюСкачать

Длина вектора

Для обозначения длины вектора используются две вертикальные линии слева и справа | AB |.

Видео:Координаты вектора. 9 класс.Скачать

Нулевой вектор

Нулевой вектор обычно обозначается как 0 .

Длина нулевого вектора равна нулю.

Видео:Вектор А - ЛюдиСкачать

Коллинеарные вектора

рис. 2

Видео:Вектор А - Зависал (official video)Скачать

Сонаправленные вектора

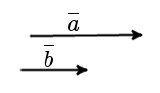рис. 3

Видео:Вектор А - ОдинСкачать

Противоположно направленные вектора

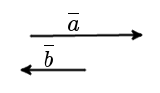рис. 4

Видео:Понятие вектора. Коллинеарные вектора. 9 класс.Скачать

Компланарные вектора

рис. 5

Всегда возможно найти плоскости параллельную двум произвольным векторам, по этому любые два вектора всегда компланарные.

Видео:ВЕКТОРЫ 9 класс С НУЛЯ | Математика ОГЭ 2023 | УмскулСкачать

Равные вектора

рис. 6

То есть, два вектора равны, если они коллинеарные, сонаправленые и имеют равные длины:

a = b , если a ↑↑ b и | a | = | b |.

Видео:Координаты вектора в пространстве. 11 класс.Скачать

Единичный вектор

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.