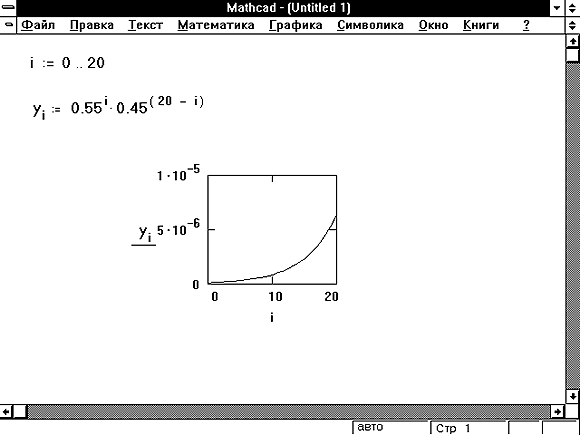
Возможно также представить графически элементы вектора. Такой график показан на Рисунке 4. Для его создания сделайте следующее:
- Определите дискретную переменную i, являющуюся нижним индексом каждого элемента, которые нужно начертить.
- Определите вектор yi. Используйте клавишу левой скобки [ , чтобы создать нижний индекс.
- Нажмите @ для создания бланка графика.
- Разместите в среднем поле вертикальной оси и i в среднем поле горизонтальной оси.
- Нажмите [F9], чтобы увидеть график.
Рисунок 4: Графическое представление вектора.
Нижние индексы должны быть неотрицательными целыми числами (или целыми, большими или равными ORIGIN, если ORIGIN 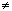
Если имеется набор данных, для которых нет подходящей функциональной связи, как на Рисунке 4, но их слишком мало, чтобы использовать файлы данных, можно использовать таблицу ввода для создания вектора.
Отображение одного вектора относительно другого
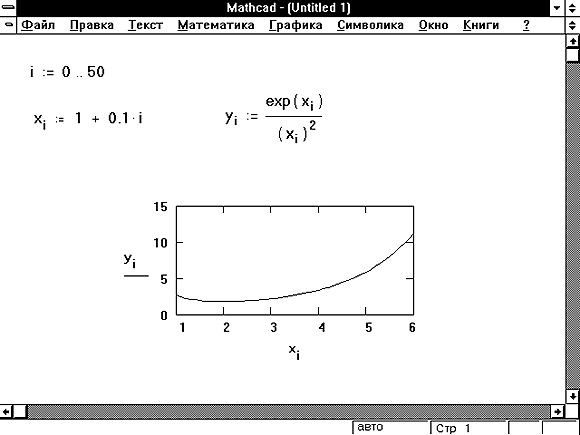
Рисунок 5 показывает, как отобразить один вектор относительно другого. Векторы не должны быть одной длины. Требуется только:
- Оба вектора должны совместно использовать один и тот же нижний индекс. Например, нельзя начертить xi относительно yj, потому что i и j — различные индексы.
- Каждое значение нижнего индекса должно соответствовать некоторому элементу в каждом векторе. Например, если x имеет только два элемента, и y имеет восемь элементов, а дискретная переменная изменяется от 0 до 7, появится сообщение об ошибке “индекс вне границ” .
Чтобы создать график, показанный на Рисунке 5, сделайте следующее:
- Определите дискретную переменную i, являющуюся нижним индексом каждого отображаемого элемента.
- Определите массивы xi и yj. Используйте клавишу левой скобки [ для написания индекса.
- Нажмите @ , чтобы создать бланк графика.
- Поместите yi в среднем поле оси ординат и xi в среднем поле оси абсцисс.
- Нажмите [F9], чтобы увидеть график.
Хотя вектор x на Рисунке 5 представляет набор равномерно располагаемых значений, это не является необходимым. Требуются только, чтобы индекс i представлял собой равномерно расположенные целые числа. Подобного ограничения не существует для xi. Это позволяет использовать на оси абсцисс не только целые числа и при этом удовлетворить требованию целочисленности нижних индексов. На Рисунке 5 yi вычисляется непосредственно через xi. Можно было бы вычислять x и y независимо из третьей переменной. Если только два вектора используют одну и ту же дискретную переменную, можно отобразить их на одном графике.
Рисунок 5: Совместное графическое представление двух векторов.
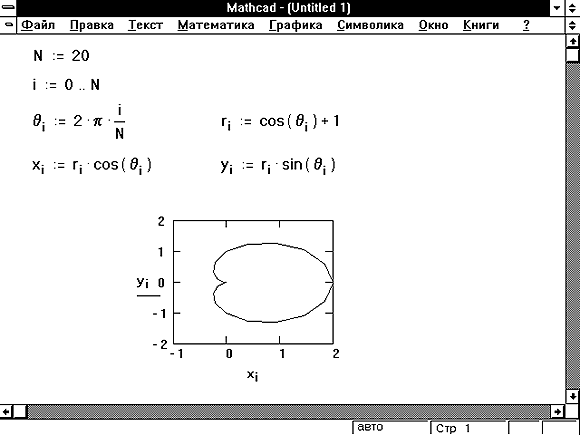
Рисунок 6: Два вектора, вычисленные независимо.
Рисунок 6 показывает график в полярных координатах, в котором и x и y зависят от переменных r и q . На Рисунке 6 с использованием векторов решена та же самая задача, которая была решена с использованием функций на Рисунке 3.
Обратите внимание, что на Рисунке 6 дискретная переменная i должна принимать целочисленные значения и используется, чтобы определить вектор q равномерно располагаемых нецелых чисел. На Рисунке 3 q определялся непосредственно как дискретная переменная. Это было возможно потому, что функции не требуют целочисленных аргументов, как векторы требуют целочисленных нижних индексов.
Графическое представление файлов данных
Можно использовать функции READ и READPRN Mathcad, чтобы импортировать данные из текстовых файлов в ASCII-формате из любой электронной таблицы, базы данных или текстового редактора, способных к экспорту данных в текстовом формате. После импорта данных Mathcad отображает их так же, как если бы это были данные, созданные в Mathcad.
Например, вот как можно отобразить данные из электронной таблицы:
- Сохраните электронную таблицу как текстовый файл ASCII с расширением .prn .
- Используйте функцию READPRN, чтобы импортировать .prn файл в Mathcad как матрицу. См. подраздел “Считывание матрицы с помощью функции READPRN” .
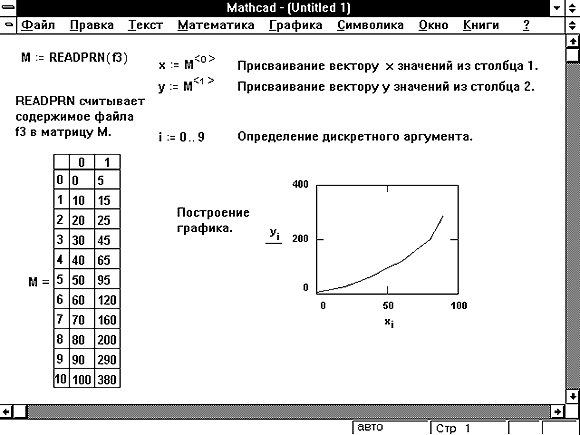
- Рисунок 7 показывает процесс графического представления векторов из данных, импортируемых из .prn файла.
Рисунок 7: Графическое представление импортированных векторов
Графическое представление других выражений
Рисунки 2-6 показывают некоторые из наиболее употребительных типов графиков. Еще один пример на Рисунке 12 показывает нанесение на график константы, используемой как риска на графике другой функции. Возможные графики не исчерпываются этими примерами. Можно отобразить на графике любое множество точек, координаты которых вычисляются любой парой выражений, лишь бы только эти выражения использовали одни и те же дискретные аргументы.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
- Построение графиков в MathCad
- Построение графика по точкам
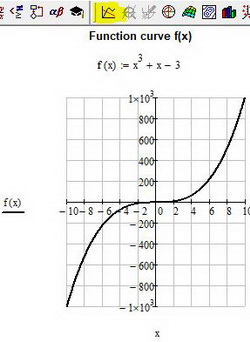
- Построение графика функции f(x)
- Построение эпюры в mathcad
- Построение графика в полярных координатах в mathcad
- График вектора в mathcad
- Mathcad для студентов
- Mathcad для начинающих
- Скачать программы бесплатно
- Построение поверхностей в Mathcad
- Графические возможности в Mathcad
- Графики в декартовой системе координат в Mathcad
- Графики в полярной системе координат в Mathcad
- Графики в Mathcad
- Построение графиков в декартовой системе координат
- Построение графиков в полярной системе координат
- Дополнительные графические возможности
- Построение поверхностей
- Дополнительные графические возможности
- Если у Вас на ноутбуке не выводятся графики поверхности или 3D графики в Mathcad, то как это устранить?
- 🌟 Видео
Видео:Функции для работы с матрицами и векторами в MathCAD 14 (21/34)Скачать
Построение графиков в MathCad
В статье рассмотрены основные возможности построения графиков в программе mathcad. Для инженерных и студенческих расчетов, как правило, достаточно знать следующие методы построения графиков:
Видео:Основы работы в Mathcad ГрафикиСкачать

Построение графика по точкам
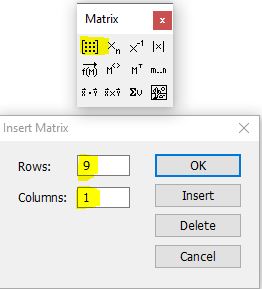
Чтобы построить график по точкам в декартовой системе координат необходимо задаться исходными данными. Создадим две матрицы-столбца, назовем их X и Y соответственно и заполним их значениями. Для создания матриц-столбцов воспользйтесь панелью Matrix. В панели matrix нажмите на кнопку под названием Matrix and vector. В появившемся окне введите количество строк и столбцов. Для матрицы-столбца количество столбцов будет очевидно ровно одному. Количество строк зависит от количества точек. В нашем случае это 9 точек. После внесения данных нажмите ОК (см. рис. 1)
Рис. 1. Создание матриц-столбцов
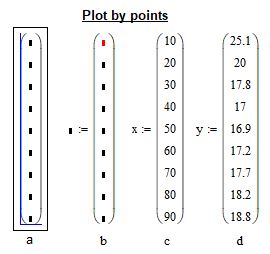
В свободном поле mathcad появится пустая матрица-столбец. Поместите курсор в матрицу и с использованием клавиш «стрелка» и «пробел» добейтесь положения курсора, как показано на рисунке 2а ниже. После чего введите с клавитуры символ двоеточия «:«. У вас должна получиться маска как на рисунке 2b. Теперь вы можете присводить содержимое матрицы какой то переменной. Например переменной X (см. рис. 2c). Заполните матрицу в соответсвии с рисунком 2 и затем повторите те же самые действия для создания матрицы-столбца Y.
Рис. 2. Заполнение матриц-столбцов для графика
На панели Graph найдите кнопку X-Y plot и щелкните по ней левой кнопкой мыши. У вас появится маска для построения графика. В черных прямоугольниках можно вводить имена осей абсцисс и ординат, а так же область отображения кривой графика (см. рис. 3)
Рис. 3. Создание заготовки для графика
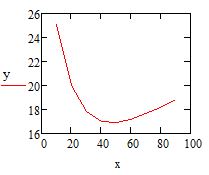
Введите под осью абсцисс имя матрицы-столбца X, а слева от оси ординат имя матрицы-столбца Y. В окне графика вы увидите ломаную линию, соединящие координаты, указанные в матрицах столбцах (см. рис. 4)
Рис. 4. График по точкам
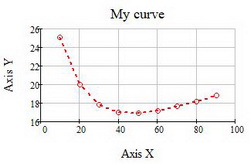
Оформление кривой графика по умолчанию, как правило, лишено наглядности и читабельности. Средства mathcad позволяют настраивать отображение графиков. Для этого щелкните 2 раза левой кнопкой мыши по изображению графика и в появившемся окне настройте внешний вид кривой, координатных осей и прочих элементов. Возможности mathcad позволяют: изменять цвет линий, их толщину и тип; нанести сетку на поле графика; подписывать оси координат; изменять формат числовых данных; вводить дополнительную (вторичную, второстепенную) ось ординат. После настройки всех элементов нажмите ОК и вы заметите, что ваш график приобрел более привлекательный вид (см. рис. 5)
Рис. 5. Настройка отображения графика
Видео:7. MathCad. Векторы и матрицыСкачать

Построение графика функции f(x)
Возможно самой распространенной задачей в студенческой и инженерной практике является построение графика функции f(x). В mathcad это делается в следующем порядке. С помощью клавиатуры и панели calculator вводится функция f(x), как показано на рис. 6. Для создания функции необходимо использовать равно с двоеточием «:=» (опертор присваивания). Далее в панели Graph найдите иконку X-Y Plot, щелкните по ней и создайте заготовку для графика. В черных прямоугольниках-маркерах введите имя функции и название аргумента. После отображения кривой зайдите в свойства графика и настройте отображение вашей кривой
Рис. 6. Построение графика функции f(x)
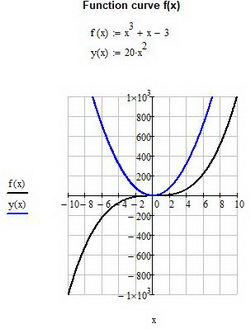
Чтобы построить два графика и более на одном поле (в тех же осях координат) сделайте следующее: введите вторую функцию, например y(x):=. , поместите курсор мыши в маркер поля графика, где уже указана первая функция f(x) и введите запятую. Таким образом mathcad зоздаст второй маркер для ввода очередной функции. Введите вашу вторую функцию и нажмите enter. Если имя аргумента обеих функций совпадает, то вторая кривая отобразится в поле графика, в противном случае, под осью абсцисс введите через запятую имя аргумента второй функции. Образец можно посмотреть ниже на рис. 7
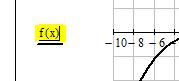

Рис. 7. Построение двух графиков функции
Видео:Форматирование трехмерного графика в MathCAD (15/34) Часть 1Скачать

Построение эпюры в mathcad
Чтобы построить классическую эпюру в mathcad нужно выполнить следующие действия:
— ввести функцию в виде y = f(x), как это показано в примерах выше;
— ввести такназываемую ранжинрованную переменную в виде i = a, a-dt..b с определенным шагом dt;
— создать поле графика и ввести туда функции f(x) и f(i) с соответствующими аргументами
— настроить визуализацию функции f(i) в соответствии с требованиями к оформлению эпюр в вашем ВУЗе или компании
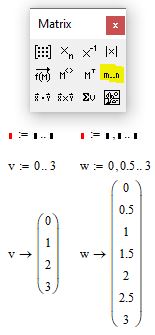
Ранжированная переменная по сути является матрицей-столбцом, разница лишь в том, что значение элементов в нее входящих представляют из себя определенную закономерность или последовательность чисел. Ранжированную переменную можно ввести воспользовавшись кнопкой Range Variable из панели Matrix. Первый маркер отвечает за начальное значение последовательности, второй — за конечное. По умолчаию шаг последовательности равен 1. Если после первого элемента ввести символ запятой и в появившемся маркере ввести следующее число вашей последовательности, то таким образом вы определите шаг, с которым будет заполняться ваша последовательность. Обратите внимание на пример ниже.
Рис. 8. Ввод ранжированной переменной
Ранжированные переменные можно использовать для построения эпюр распределения физических величин. Для этого постройте ваш исходный график одним из методов, описанных выше. Пусть это будет график f(x):=x^2. Затем создайте ранжированную переменную с шагом 0.5 как указано в примере ниже
Рис. 9. Ввод ранжированной переменной
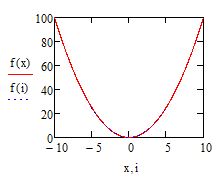
Далее создайте поле для графика и около оси ординат введите две функции: f(x) и f(i). Под осью абсцисс также введите соответсвующие аргументы: x и i. Вы должны увидет обычную параболу как на рисунке ниже
Рис. 10. Построение эпюры. Шаг 1
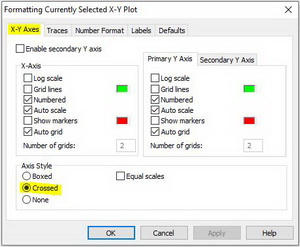
Для получения эпюры нужно настроить отображение функции f(i) в свойствах графика. Щелкните 2 раза по графику чтобы вызвать меню настройки отображения графика. Перейдите во вкладку traces. В списке Legend Label найдите имя trace 2. В столбце Type для trace 2 из выпадающего списка выберете тип графика stem. В столбце Symbol уберите отображение элементов. Во вкладке X-Y Axes выберете для Axis Style тип Crossed. Нажмите ОК и вы увидете эпюру. Вы можете настроить ее внешний вид по желанию.
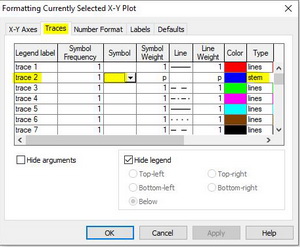
Рис. 11. Построение эпюры. Шаг 2
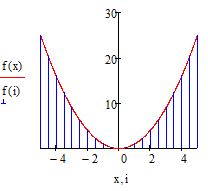
В итоге вы увидите, что на графике появились вертикальные линии, которые распределены по оси абсцисс с шагом, который вы указали в ранжированной переменной. Изменяя параметры этой переменной можно настроить отображение эпюры. Эпюра готова (см. рис. 12)
Рис. 12. Построение эпюры. Шаг 3
Видео:Построение трехмерного графика в MathCAD 14 (14/34)Скачать
Построение графика в полярных координатах в mathcad
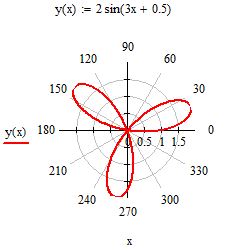
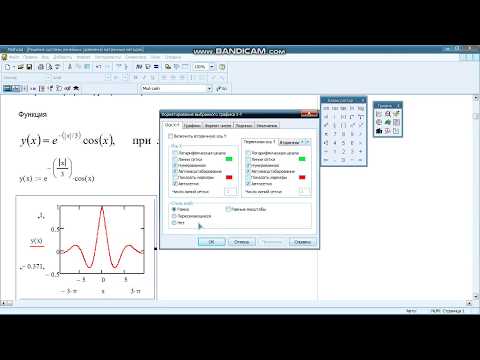
Введите функцию, которую необходимо построить в полярных координатах. Для примера возьмем y(x):=2*sin(3*x+0.5)
Для построения графика в полярных координатах нажмите кнопку Polar Plot из панели Graph
Рис. 13. Создание загатовки для графика в полярных координатах
Вы увидете пустое поле графика. В черном маркере слева введите имя введенной функции y(x). В маркере снизу введите аргумент x и нажмите enter. Вы увидете «трилистник». Внешний вид графика можно настроить щелкнув два раза по графику левой кнопкой мыши. В появившемся окне представлен широкий набор инструментов для настройки отображения.
Рис. 14. Построение графика в полярной системе координат
Donec eget ex magna. Interdum et malesuada fames ac ante ipsum primis in faucibus. Pellentesque venenatis dolor imperdiet dolor mattis sagittis. Praesent rutrum sem diam, vitae egestas enim auctor sit amet. Pellentesque leo mauris, consectetur id ipsum sit amet, fergiat. Pellentesque in mi eu massa lacinia malesuada et a elit. Donec urna ex, lacinia in purus ac, pretium pulvinar mauris. Curabitur sapien risus, commodo eget turpis at, elementum convallis elit. Pellentesque enim turpis, hendrerit tristique.
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Duis dapibus rutrum facilisis. Class aptent taciti sociosqu ad litora torquent per conubia nostra, per inceptos himenaeos. Etiam tristique libero eu nibh porttitor fermentum. Nullam venenatis erat id vehicula viverra. Nunc ultrices eros ut ultricies condimentum. Mauris risus lacus, blandit sit amet venenatis non, bibendum vitae dolor. Nunc lorem mauris, fringilla in aliquam at, euismod in lectus. Pellentesque habitant morbi tristique senectus et netus et malesuada fames ac turpis egestas. In non lorem sit amet elit placerat maximus. Pellentesque aliquam maximus risus, vel venenatis mauris vehicula hendrerit.
Interdum et malesuada fames ac ante ipsum primis in faucibus. Pellentesque venenatis dolor imperdiet dolor mattis sagittis. Praesent rutrum sem diam, vitae egestas enim auctor sit amet. Pellentesque leo mauris, consectetur id ipsum sit amet, fersapien risus, commodo eget turpis at, elementum convallis elit. Pellentesque enim turpis, hendrerit tristique lorem ipsum dolor.
Видео:Основные действия с матрицами и векторами в MathCAD 14 (20/34)Скачать

График вектора в mathcad
Видео:MathCAD Построение графика быстрым способомСкачать
Mathcad для студентов
Видео:Матрицы. Скалярное и векторное произведение векторов в Mathcad, матричные функции(Урок 3.3)Скачать
Mathcad для начинающих
Видео:Как построить график по точкам в MathcadСкачать
Скачать программы бесплатно
Видео:Векторная диаграмма токов в программе MathcadСкачать

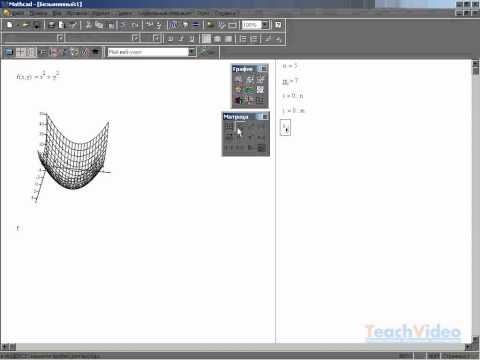
Построение поверхностей в Mathcad
Для построения трехмерной поверхности F(x,y) в Mathcad, функция предварительно представляется матрицей М ординат F(x,y). При этом выводится шаблон графика, левый верхний угол которого помещается в место расположения курсора. Шаблон содержит единственное поле — темный прямоугольник у левого нижнего угла основного шаблона. В него надо занести имя матрицы М или имя функции F при автоматическом построении матрицы. Наглядность представления трехмерных поверхностей в Mathcad зависит от множества факторов: масштаба построений, углов поворота фигуры относительно осей, применения алгоритма удаления невидимых линий или отказа от него, использования функциональной закраски и т.д. Для изменения этих параметров в Mathcad следует использовать операцию установки формата графика. При построении трехмерных поверхностей и объемных фигур можно использовать параметрическое задание описывающих их функций. Фигуры задаются значениями координат х, у и z всех точек фигуры. При этом в шаблоне 3D-графики Mathcad указываются три матрицы, хранящие массивы этих координат, — X, Y и Z. На листинге приведены примеры построения графиков поверхностей.
В Mathcad можно изменять заданные по умолчанию параметры графиков. Для этого необходимо вызвать окно диалога форматирования трехмерных графиков (3-D) двойным щелчком мыши по полю графика. Диалоговое окно 3-D Plot Format содержит множество флажков для выбора режима построения графика и девять закладок:
- Backplanes ( Основание );
- Special ( Специальный );
- Advanced ( Дополнительно );
- QuickPlotData ( Графические данные );
- General ( Общее );
- Axes ( Ось );
- Appearance ( Внешний Вид );
- Lighting ( Освещение );
- Title (Название).
Ограничимся рассмотрением одной вкладки, представленной на рис., — General (Общее). Первый комплект чисел в разделе View (Вид) показывает Rolation (Вращение) , Tilt (Наклон) , Twist (Искривление), Zoom (Масштаб), под которыми наблюдается построенный график поверхности. Далее в разделе Axes Style (Стиль оси) имеется ряд переключателей и флажок для выбора стиля изображения размеров графика:
- Perimetr (периметр) – выводит график с размерами по периметру;
- Corner (угол) – выводит график с размерами по осям;
- None (нет) – выводит график без размеров по периметру и по осям;
- Equal scales (равные шкалы) – установка по осям равных масштабов. В пункте Frames (Границы графика) определяется обрамление графика:
- Border (границы) – показывает границы графика;
- Show Box (каркас) – показывает график в виде параллелепипеда. На панели переключателей Plot 1 (График 1) можно выбрать одну из форм представления трехмерного графика. При работе с панелями настройки параметров изображения можно посмотреть результат, полученный при изменении параметра изображения, не закрывая панели. Для этого после изменения параметра щелкните по кнопке Применить. Для возвращения в документ щелкните мышью по кнопке ОК.
Видео:MathCAD Построение графика по данным из массиваСкачать
Графические возможности в Mathcad
Графические возможности в математическом пакете Mathсad позволяют создавать:
- контурный график — поверхностей одинакового уровня (изолинии);
- график в виде точек в трехмерном пространстве;
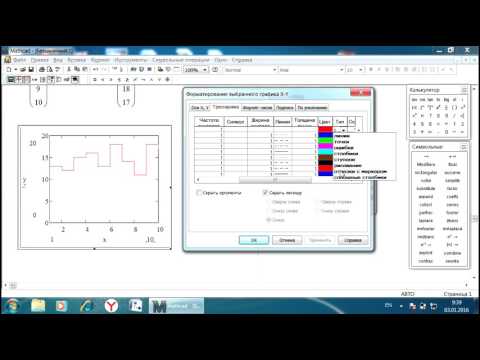
- столбиковую гистограмму;
- графика векторного поля на плоскости.
Данные графические зависимости носят специализированный характер, и это предопределяет их более узкое использование на практике. Контурный график в Mathcad представляет собой совокупность линий, каждая из которых соответствует одинаковому значению функции, зависящей от двух переменных (изолинии). Такие функции получили широкое распространение в картографии, геодезии, океанологии, экологии и т. д. Последовательность построения контурного графика следующая. Сначала вводится функция двух переменных f(x,y). Далее определяются значения хi , yj , задающие дискретные точки по осям х, у. Заполняется матрица М значениями f(хi,yj). Отображается матрица М в виде карты изолиний. На листинге приведен пример построения контурного графика.
Форматирование изображения (количество линий уровня их значения, заливка) в Mathcad производится посредством диалогового окна 3-D Plot Format (Форматирование), которое представлено на рис. Переключатели диалогового окна позволяют сформировать дизайн графика. Например, переключатели группы Contour Options (Контурные опции) устанавливают следующие опции графика:
- Fill (Залить) – обеспечивают закраску графика согласно цветовой палитры.
- Draw Lines (Рисовать линии) – позволяет отображать на графике лини уровня.
- Auto Contour (Автоконтур) – количество линий контура выбирается автоматически.
- Numbered (Пронумерованные) – на линии уровня выносятся их числовые значения.
На листинге представлены графики функций, демонстрирующие графические возможности в Mathсad при построении столбиковых гистограмм, точечных диаграмм, векторного поля. Один вид 3-D диаграмм функции 2-х переменных может быть трансформирован в другой вид посредством вкладки General (Общее) диалогового окна 3-D Plot Format. Для преобразования диаграммы в другой вид необходимо выделить график и установить соответствующий переключатель группы Display As. При этом диаграмма принимает вид, соответствующий установленному переключателю:
- Surfase Plot – график поверхности.
- Contour Plot – контурный график.
- Data Points – точечный график.
- Vector Fields Plot – векторное поле.
- Bar Plot – столбиковая гистограмма.
- Patch Plot – “Кусочный” график (совмещенный график поверхности и точечный график).
Видео:Mathcad Prime. Урок 2 - Построение графиковСкачать

Графики в декартовой системе координат в Mathcad
График в декартовой системе координат в Mathcad представляет собой незаполненный шаблон в виде большого прямоугольника с темными маленькими прямоугольниками, расположенными около осей абсцисс и ординат будущего графика.
В средние прямоугольники надо поместить имя аргумента x оси абсцисс и имя функции у оси ординат. Если в Mathcad строятся графики нескольких функций в одном шаблоне, то для их разделения следует использовать запятые. Крайние темные маленькие прямоугольники служат для указания предельных значений абсцисс и ординат, т.е. они задают масштабы графика. Если оставить эти шаблоны незаполненными, то в Mathcad масштабы по осям графика будут устанавливаться автоматически. Но автоматические масштабы могут оказаться не вполне удобными. Поэтому рекомендуется вначале использовать автоматическое масштабирование, а затем изменять их на более подходящие. На листинге показаны пример построения графиков.
Чтобы произошло построение графика в автоматическом режиме вычислений в Mathcad, достаточно вывести курсор за пределы графического объекта. Параметры изображения (цвет и толщина линий, координатная сетка, разметка осей, надписи на графиках и др.) проще всего изменить, щелкнув дважды по полю графика. В результате активизируется диалоговое окно “Форматирование”, на котором в Mathcad выбирается соответствующая вкладка и устанавливаются параметры настройки графика. Возможно отображение на одном шаблоне графиков функций от различных переменных. В этом случае, количество переменных и функций, их имена и порядок следования должны быть синхронизированы.
Видео:MathCAD График функции пользователя с условиемСкачать

Графики в полярной системе координат в Mathcad
Графики в полярной системе координат в Mathcad строятся аналогично графикам в декартовой системе координат. Но при этом необходимо учитывать специфику самих функций. В полярной системе координат при активизации шаблона графика, рабочее поле представлено окружностью. В нижней части шаблона задается имя угловой переменной, в левой части — имя функции, определяющей радиус как функцию угла. В правой верхней части расположены два поля для задания нижнего и верхнего значения радиуса. В Mathcad возможно отображение нескольких функций в рабочем поле графика. Для этого имена функций так же вводятся через запятую. На листинге представлены примеры отображения функций в полярной системе координат. Предусмотрена возможность форматирования графиков функций путем вывода шкал радиальных, круговых, вспомогательных линий и т.д. Форматирование в Mathcad обеспечивается с помощью инструментов диалогового окна Форматирование, которое активизируется двойным щелчком мыши по полю графика.
Видео:Как строить графики переходных процессов в программе маткадСкачать

Графики в Mathcad
График в математическом пакете Mathсad строится с использованием шаблонов. Для начального построения графика достаточно войти в меню Вставка, График или задать тип графика на панели инструментов “Графики” и выбрать один из семи основных типов графиков:
Построение графиков в декартовой системе координат
В пакете Mathcad незаполненный шаблон графика представляет собою большой пустой прямоугольник с темными маленькими прямоугольниками. Они расположены около осей абсцисс и ординат будущего графика.
Построение графиков в полярной системе координат
Для построения в Mathcad трехмерной поверхности F(x,y) функция в начале представляется матрицей М координат F(x,y).
Дополнительные графические возможности
В данном разделе показаны графические возможности Mathсad по созданию контурного графика..
Построение поверхностей
Для построения трехмерной поверхности F(x,y).
Дополнительные графические возможности
В данном разделе показаны графические возможности Mathсad по созданию контурного графика..
Если у Вас на ноутбуке не выводятся графики поверхности или 3D графики в Mathcad, то как это устранить?
Одна из причин не отображения графиков поверхности или 3D графиков это «Качество цветопередачи«.
🌟 Видео
Дискретные переменные в MathCAD 14 (9/34)Скачать

Mathcad. Вывести таблицу и графикСкачать

MathCAD Построение графика поверхности быстрым способомСкачать
Плоский график функции в MathCAD 14 (10/34)Скачать

mathcad график кусочно-заданной функцииСкачать