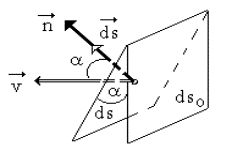
Плотность потока энергии j волны с объемной плотностью энергии вектор умова (3 видео)

Поток энергии. Вектор Умова — Пойнтинга

Если на пути распространения волны поставить некоторую площадку dS, то в этом случае говорят о потоке энергии через эту площадку.

Отношение энергии, переносимой сквозь некоторую площадку к промежутку времени, за который произошел ее перенос, называют потоком энергии.

Согласно определению можно записать формулу потока энергии:

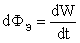Плотность потока энергии j волны с объемной плотностью энергии вектор умова

(7.23)

Используя объемную плотность энергии w, запишем полную энергию волны

dW= w (vdt) dS сos a,

где ℓ = vdt — расстояние, на которое перемещается волна, имея скорость v за малое время dt; a — угол между векторами скорости и нормали к площадке (рис. 7.6)

Рис. 7.6

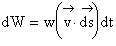
где .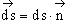

Следовательно, поток энергии переносимый волной

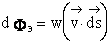(7.24)

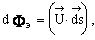(7.25)

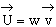(7.26)

называют вектором Умова-Пойнтинга, или вектором плотности потока энергии.

Вывод: Модуль вектора Умова-Пойнтинга характеризует плотность потока энергии волны, переносимой через площадку перпендикулярно направлению распространению волны т.е.,

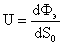
Мощность потока энергии волны характеризуют интенсивностью волны J.

Модуль среднего значения вектора плотности потока энергии волн называют интенсивностью.

Интенсивность волны — энергия, переносимая волной через единицу поверхности за единицу времени перпендикулярно к направлению распространению волны.

Для плоской бегущей и сферической синусоидальных волн за период интенсивность волны определяется выражением

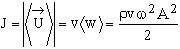(7.27)

Реальные среды, в которых распространяются волны, всегда поглощают энергию. При этом происходит уменьшение амплитуды и интенсивности волны, т.е. волны затухают.

Видео:Билет №38 "Поток энергии"Скачать

Энергия упругой волны. Поток и плотность потока энергии. Вектор Умова

Упругая среда, в которой распространяются механические волны, обладает как кинетической энергией колебательного движения частиц, так и потенциальной энергией, обусловленной деформацией.

Рассмотрим продольную плоскую волну (8.2), которая распространяется в единице объема среды массой, равной р, с колебательной скоростью и = d^/dt , где | — смещение частиц среды. Выделенный объем обладает кинетической энергией. Объемная плотность кинетической энергии среды выражается как

где dV_k — кинетическая энергия всех частиц в малом объеме dV среды, выбранном таким образом, что в его пределах скорость и всюду одинакова; р — плотность среды; и — скорость колебания частиц среды.

Можно доказать, что объемная плотность потенциальной энергии упругодеформированной среды

где dV_p — потенциальная энергия однородно деформированного малого участка среды объемом dV v — фазовая скорость волны в среде; с — относительная деформация среды.

Поскольку волна движется, то она осуществляет перенос механической энергии. Под объемной плотностью энергии упругих волн понимают объемную плотность механической энергии среды, обусловленную распространением этих волн:

Продифференцировав уравнение плоской волны (8.4) один раз по /, другой раз по х и определив таким образом и и с, с учетом того, что k 2 v 2 = о) 2 , получим плотность энергии, возникающей в упругой среде при распространении в ней плоской продольной волны:

Рис. 8.3. Через площадку среды dS за время dt волной переносится энергия dW

В физике используют понятие потока энергии. Если площадка среды имеет площадь dS, а ее нормаль п составляет с направлением распространения волны (осью X) угол а (рис. 8.3), то поток энергии d 2, с)).

Когда волна распространяется в трехмерном пространстве, тогда поток энергии через произвольную поверхность S выражается в виде интеграла:

Эффект Доплера для звуковых волн. При движении источника колебаний и приемника (устройства, которое воспринимает звуковые колебания среды) друг относительно друга происходит изменение частоты колебаний, воспринимаемой приемником. Это явление называется эффектом Доплера.

В акустике эффект Доплера проявляется как повышение тона звука при приближении источника звука к приемнику и понижение тона при удалении источника от приемника.

Пусть источник и приемник (наблюдатель) движутся вдоль соединяющей их прямой: и_и и v_u — соответственно скорости источника и приемника (положительны при сближении и отрицательны при удалении источника и приемника); v₀ — частота колебаний источника; и — скорость распространения звука в данной среде. Если направления у_и и v_u не совпадают с проходящей через источник и приемник прямой, то берут их проекцию на направление этой прямой.

В общем случае частота воспринимаемых приемником колебаний

Видео:4.8 Плотность потока мощности электромагнитной волныСкачать

Плотность потока энергии волны. Интенсивность волны

Распространение волн всегда связан с переносом энергии, который количественно характеризуется потоком энергии Ф, плотностью потока энергии J и интенсивностью волны I.

Рассмотрим волну, распространяющуюся вдоль оси о х со скоростью v (рис.210). Волна за время A t распространяется на расстояние, равное v • A t. Построим параллелепипед с основаниями A S, перпендикулярными оси ох, и длиной v — At.

Вся энергия волны, заключённая в параллелепипеде, за интервал времени A t пройдёт через правое основание A S. Обозначим энергию, переносимую волной сквозь площадку A S, через A W. Она равна произведению объёмной плотности полной энергии со _пол волны на объём параллелепипеда А V.,

Если объём V,, параллелепипеда мал, то объёмную плотность энергии со _пол волны можно считать одинаковой во всех точках рассматриваемого объёма.

Количество энергии, переносимое волной за единицу времени через поверхность AS, расположенную перпендикулярно направлению распространения волны, называется потоком Ф энергии волны

Поток энергии Ф в системе СИ измеряется в ваттах

(7 Вт =1 Л ж ). Поток энергии Ф волны может изменяться от одной

точки среды к другой. В этом случае используется векторная величина, называемая вектором плотности потока энергии J. Он был введён в 1874 г. профессором Московского университета Н. А. Умовым, поэтому назван вектором Умова.

Вектор Умова (вектор плотности потока энергии J) численно равен энергии, переносимой волной через единичную площадку, расположенную перпендикулярно направлению потока энергии в данной точке среды, за единицу времени

Запишем уравнение (20.56) в векторной форме

Вектор Умова, как и объёмная плотность полной энергии со ,_Ю1 волны, может иметь разные значения в разных точках пространства. В рассматриваемой точке среды вектор Умова изменяется со временем по такому же закону, как и объёмная плотность полной энергии со ,_Ю1 волны. Поэтому величина плотности потока энергии У через любую площадку (х = с о п s t), расположенную перпендикулярно направлению распространения волны, со временем периодически возрастает от нуля (У = 0) до максимального значения (У = У _тах).

В теории волн используется понятие среднего значения

плотности потока энергии за период времени Т (Т = xIL) в

где _пош) — среднее за период Т значение объёмной плотности

определённой точке пространства (х = с о п s t), которое назвали интенсивностью волны I

энергии волны в данной точке среды.

Подставим в (20.59) формулу (20.53)

Здесь учли, что среднее значение квадрата синуса за период Т равно 1.

Запишем формулу для интенсивности I волны, принимая во внимание выражение (20.60)

Отсюда следует, что интенсивность I волны прямо пропорциональна квадрату амплитуды А

Когда волна распространяется в трёхмерном пространстве, то поток энергии Ф через произвольную поверхность S определяется по формуле

где d S = п ? d S, п нормаль к поверхности S.

Плотность потока энергии J и интенсивность I в системе СИ

имеют размерность — ватт на квадратный метр | ^ т ].

Проведём две волновые поверхности в виде сфер, с радиусами г; и г₂. Считаем, что энергия волны не поглощается средой, тогда средние значения энергии, проходящей через волновые поверхности, равны

где S/, S₂ — площади сфер радиусами Г/ и г₂. Подставим в (20.62) интенсивности //, 1₂

сократив на р, у, со , получим

Итак интенсивность I сферической волны убывает по мере удаления от точечного источника по закону

где I 00), I (г) — интенсивность волны на расстояниях г = 1 м и произвольном расстоянии г от источника волны. Уравнение (20.65) следует из (20.63) и (20.64), записанных для двух расстояний г = 1 м и г > 1 м.

Зависимость амплитуды А и интенсивности I сферической волны от расстояния г от источника волны объясняются тем, что по мере удаления фронта волны от источника волн в колебательное движение за равные промежутки времени вовлекаются всё возрастающие объёмы среды.

Уравнение сферической волны записывается в виде

где г — расстояние от источника волн до рассматриваемой точки среды.

Интенсивность I и амплитуда А плоской волны, распространяющейся в среде, не поглощающей энергию волны, не изменяются при удалении от источника волн. Это связано с тем, что в колебательное движение за равные промежутки времени вовлекаются равные объёмы среды.

Интенсивность I плоской волны, распространяющейся в поглощающей среде вдоль положительного направления оси о х, изменяется, как и амплитуда волны по экспоненциальному закону