Геометрический смысл собственного вектора матрицы (7 видео)

Собственные значения и собственные векторы

Пусть /д(А) = det (4 — XI) — характеристический многочлен матрицы А порядка п над полем Р. Предположим, что он имеет корень, принадлежащий полю Р. Обозначим этот корень той же буквой Л, т. е. далее полагаем, что Л — это число из поля Р. Поскольку det (4 — XI) = 0, однородное уравнение (4 — Х1)х = О имеет нетривиальное решение х G Р» и, следовательно,

Соотношение (*) можно рассматривать и без какой-либо связи с характеристическим многочленом. Более того, оно имеет смысл, если считать, что 4 — некоторый линейный оператор на каком-то пространстве V над полем Р, х G V и А е Р. Число Л и вектор х 0, связанные соотношением (*), называются собственным значением и собственным вектором матрицы или оператора 4.

Связь собственных значений и корней характеристического многочлена описывается следующим, в действительности уже полученным нами, утверждением.

Видео:Собственные значения и собственные векторы матрицы (4)Скачать

Утверждение 5.5.1. Собственные значения линейного оператора на конечномерном пространстве и только они являются корнями его характеристического многочлена.

Обратим внимание на ясный геометрический смысл собственного вектора: при действии на него оператором 4 он просто умножается на соответствующее ему собственное значение.

Если в пространстве V имеется базис из собственных векторов оператора, то в этом базисе данный оператор представляется, очевидно, диагональной матрицей. Такой оператор называется оператором простой структуры или диагонализуемым оператором.

Простым достаточным условием диагонализуемости является простота собственных значений и предположение о том, что поле разложения характеристического многочлена содержится в поле Р. Собственное значение называется простым, если оно является простым корнем характеристического многочлена. В противном случае собственное значение называется кратным. Говорят, что собственное значение имеет алгебраическую кратность к, если для характеристического многочлена оно является корнем кратности к. Упомянутое выше условие диагонализуемости вытекает из следующей теоремы.

Теорема 5.5.1. Если собственные векторы х. Хк линейного оператора А соответствуют попарно различным собственным значениям Х. Хк, т о они линейно независимы.

Видео:Собственные векторы и собственные значения матрицыСкачать

Доказательство. Рассмотрим равную нулю линейную комбинацию данных собственных векторов и подействуем на нее оператором А:

Из последнего равенства вычтем равенство

хь (IZaiXi)= 0 52

Далее очевидным образом применяется индукция по к. ?

Пусть Л — собственное значение линейного оператора А: V V. Множество L всех векторов х eV, таких что Ах = Хх, называется собственным подпространством оператора А, отвечающим данному собственному значению Л. То, что L будет подпространством в V, проверяется тривиальным образом. Каждый ненулевой вектор из L является собственным вектором для Л, и очевидно, что L содержит все собственные векторы, соответствующие Л. Размерность пространства L называется геометрической кратностью собственного значения Л.

Видео:Собственные значения и собственные векторыСкачать

Утверждение 5.5.2. Геометрическая кратность собственного значения меньше или равна его алгебраической кратности.

Доказательство. Пусть линейный оператор А действует в n-мерном пространстве V над полем Р, и пусть Л1 — его собственное значение геометрической кратности I. Выберем базис е. ,е_п пространства V таким образом, чтобы векторы е. ,е/ составили базис собственного подпространства для Ль В этом базисе матрица оператора А примет вид

И]е =

Поэтому характеристический многочлен представляет собой произведение

det (411 — AZ/) det (4₂2 — = (Ai — A) z det (Д₂₂ — AZ_n_/).

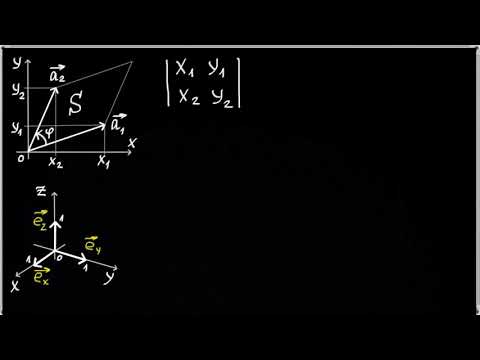
Видео:2018-10-14. Геометрический смысл определителя 2х2Скачать

Отсюда видно, что l не может быть больше алгебраической кратности корня Ль ?

Вопрос о существовании собственных значений, а значит и собственных подпространств, — это вопрос о том, имеет ли характеристический многочлен корни в поле Р. Мы уже знаем, впрочем, что всегда можно перейти к более широкому полю разложения характеристического многочлена, в котором он будет иметь п корней с учетом кратностей. Довольно естественным образом исходное n-мерное пространство V можно сделать подмножеством нового n-мерного пространства над этим более широким полем и доопределить действие оператора на новом пространстве.

Задача 208. Пусть А — матрица порядка п и ранга г. Докажите, что матрица I А А имеет собственное значение 1 алгебраической кратности не меньше п — г.

Задача 209. Матрица А = [а^] порядка п имеет верхний почти треугольный вид, т.е. aij = 0 при i > j + 1. Кроме того, ai₊,i 0 при 1 г п — 1. Докажите, что если матрица А диагонализуема, то она имеет п попарно различных собственных значений.

Задача 210. Докажите, что диагонализуемая матрица ранга г обладает ненулевым главным минором порядка г.

Видео:Геометрический смысл умножения матриц. Кафедра была в ШОКЕ три неделиСкачать

Задача 211. Комплексная матрица А порядка п обратима, совпадает со своей сопряженной матрицей и известно, что окаймляющая ее матрица

также является обратимой.

[ В обратима и матрица

Докажите, что матрица

д-1

Видео:Собственные векторы и собственные значенияСкачать

имеет собственные значения 1 и (1 ± х/5)/2 алгебраической кратности п — г и г соответственно.

Задача 212. Пусть Л — собственное значение матрицы А е С пхп . Докажите, что

Задача 213. Все элементы матрицы А е IR nxn неотрицательны, а суммы элементов в каждой строке одинаковы и равны Л. Докажите, что Л является наибольшим по модулю собственным значением матрицы А.

Задача 214. Придумайте, как найти алгебраические кратности собственных значений комплексной матрицы, не вычисляя сами собственные значения. Докажите, что это можно сделать за конечное число арифметических операций.

источники: